海上船舶溢油事故多物资应急调度问题分析
2021-01-06刘晓佳李子木
刘晓佳, 汪 强,3, 李子木, 张 可
(1.集美大学 航海学院, 福建 厦门 361021;2.武汉理工大学 航运学院, 武汉 430063;3.宁波国际投资咨询有限公司, 浙江 宁波 315000)
船舶是海上重要的交通运输工具,在航行过程中可能出现碰撞、触礁、沉没和火灾等海损事故,导致储油舱和燃机舱设备破损,使未知数量的燃油泄漏至海中,发生海上溢油事故。据统计,仅在1973—2018年,我国沿海港口共发生3 336起船舶溢油事故,平均每年76起,对海洋环境产成了恶劣影响,造成了巨大经济损失。[1]海上船舶溢油事故的发生具有突发性和漂移扩散性,溢油事故应急物资不仅要满足船舶事故发生点的需求,而且要对溢油漂移后的区域进行溢油拦阻回收。若对事故处理不及时,可能会造成更深度的污染和更大的损失。因此,保证溢油应急物资调度的合理性至关重要。
目前,国内外学者已在应急物资调度和海上突发事故应急调度2个方面开展大量研究。应急物资调度方面的研究主要以运输线路最优[2]、综合评价函数最高[3]、运输费用最低[4]、单种物资运输时间最短[5]和资源分配最优[6]等为目标建立模型。海上船舶溢油事故具有特殊性,应急物资运输船舶路径受影响的程度小,且比起海上溢油事故对环境的损害和造成的经济损失,往往不会考虑运输费用,导致上述模型具有局限性。当前,针对海上溢油事故应急调度的研究较少。王晶[7]引入“物资救助包”的概念,根据陆上仓库与事故点之间的需求关系,建立按期完成救援和出救点最少的双目标规划模型,但未考虑应急储备库的初始物资储备情况。罗吴辉等[8]针对海上应急物资调度多出救点和多目标的特点,结合溢油敏感区对响应时间的限制,提出基于不同响应时间段的动态优化模型,最后采用理想点法确定调度方案。WILHELM等[9]从时效性的角度出发,建立多阶段物资分配模型,在应急响应时间最短的情况下,确保运输溢油清除设备的时间能满足应急限制期的要求。陈金晶[10]提出具有优先权的海上突发事件多物资调度方法,但未结合具体调度工具的数量制订调度方案。王军等[11]考虑到不同待围控区域有围油栏需求量及其限制期的差异,构建多供应点、多需求点的调度模型,从而确定其调度位置和数量。这些研究大都是在应急物资需求数量明确的情况下进行单种物资调度研究,未结合港口具体可调度船舶数量。
本文结合海上船舶溢油事故的特点,通过预测溢油应急物资需求点和溢油应急物资需求量,构建以所有船舶完成调度时间最短为目标的多物资、多运输船舶下的应急物资调度模型,利用遗传算法求解,最终得出具体船舶运输应急物资的调度方案。
1 问题描述
海上溢油是指进入海洋环境或河流的油,主要是指原油及其相关炼制品。[12]根据《1990年国际油污防备、反应和合作公约》对油的定义,是指任何形式的石油,包括原油、燃料油、油泥、油渣和炼制产品。溢出的油品不仅具有引发火灾的危险,而且会对海洋生态造成严重污染,破坏海洋环境,及时合理地调度溢油应急物资,对降低海上船舶溢油事故带来的安全隐患和减少对海洋生态的破坏尤为重要。
1.1 海上船舶溢油事故
在风、浪和流等环境因素的作用下,溢出的油品具有移动性。因此,在制订应急调度方案时,应设置多个应急物资需求点进行处理。当海上船舶溢油事故发生之后,陆上溢油应急物资储备库为其提供应急物资救助。整个应急物资调度过程为陆上溢油应急物资储备库Si到应急物资需求点Dj的过程,其结构见图1。
1.2 调度物资类型
不同溢油类型、气象条件、海况和溢油规模对海上溢油事故需求的物资不尽相同,主要包括以下3类需求物资:

图1 海上溢油事故应急物资调度结构
1) 拦阻溢油类物资,主要为围油栏,作用是围控、溢油导流和防止潜在溢油。
2) 回收溢油类物资,主要为收油机,作用是回收水面溢油、油水混合物。
3) 其他,主要为吸附材料和化学、生物处理剂,作用是减少溢油对环境的破坏,加速受损生态环境的恢复。
1.3 调度船舶类型
对海上船舶溢油事故进行处理,需用专业的溢油应急船舶处理溢油污染事故,实现海上溢油应急指挥、围控、回收和存储等功能。此类船舶可按应急处置需求分为溢油工作船舶和溢油应急运输船舶。溢油工作船舶从港口出发之后在事故点周围建立基站,进行溢油拦阻、回收和处理;应急运输船舶往返于事故点和应急储备库,承担溢油应急物资输送任务。[13]本文研究的主体是应急运输船舶。
2 溢油应急物资调度方法
当有海上船舶溢油事故发生时,相关部门会立即做出应急响应和处置。首先对事故点溢油源、溢油量、溢油成分、溢油扩散范围和应急物资需求量等进行预测评估;其次协调各应急储备库,对海上船舶溢油事故所需物资、装备和人员等作出相应的调度安排;最后对海上船舶溢油进行回收、恢复和重建等处置,完成整个事故处置过程。[14]
2.1 溢油漂移扩散
海上溢油漂移扩散研究主要是通过拉格朗日法和欧拉法建立溢油后油粒子运动模型进行的,其中最主流的是美国国家海洋与大气局开发的GNOME仿真软件[15],该软件可模拟风、洋流和因其他因素的变化造成的溢油扩散和转移,仿真效果较好。
2.2 三角模糊数学理论
在海上船舶溢油事故发生之后,天气、交通和灾情等信息不确定会导致应急物资需求量的预测值与实际情况有较大偏差,只能通过类比已发生的事故估计物资需求区间。但是,通过类比会使应急物资的需求存在很大的不确定性,三角模糊数能体现应急物资需求的不确定性[16],因此引入三角模糊数这一概念处理该问题。对于三角模糊数A=(a,b,c),a≤b≤c∈R,其隶属度为
(1)
对于三角模糊数的比较,可利用该模糊数的整体期望值进行去模糊化处理[17],若A为模糊数,则其整体期望值为
(2)
可得出,对于A=(a,b,c),有
(3)
2.3 理论模型
理论模型假设条件:
1) 所有的应急物资储备库的应急物资储量和物资需求点各物资需求区间均已知,且应急库总的储量可满足物资需求点的需求。
2) 已知各应急物资储备库和物资需求点之间应急物资运输船的航行距离。
3) 各运输工具均满载某单一货物正常运行,不考虑物资的混合装载。物资流为单向流,考虑到装卸时间差别不大,在模型中不作考虑,只求解最短运输时间。
4) 通过GNOME仿真软件得到物资需求点位置。假设得到仿真结果之后,需求点位置不再发生移动。
Si={s1,s2,…,sm}
(4)
式(4)为应急物资储备库信息的集合。
Dj={d1,d2,…,dn}
(5)
式(5)为物资需求点信息的集合。
w(w=1,2,…,p)为物资类型,其储存量与需求区间分别为siw和ITjw(A)。
C={c1,c2,…,cg}
(6)
式(6)为应急物资运输船舶的集合。
ck(k=1,2,…,g)为第k艘船在该次调度任务中的运输信息,其中该船舶的载货量为dk,航速为vk,数量为nk,即
ck={dk,vk,nk}
(7)
L为应急物资储备库和物资需求点之间路程的矩阵,有
(8)
twh为在整个调度过程中第h艘船舶运输w类型物资的总工作时间,有
(9)
T为船舶调度时间的集合,有
T={tw1,tw2,…,twh}
(10)
整个调度过程的完成时间为
TS=max(twh)
(11)
目标函数为
min(Ts)
(12)
约束条件为
(13)
(14)
式(12)~式(14)中:式(12)为完成整个调度过程所需最短时间;式(13)为应急储备库的w类型物资总供应量大于等于事故点的对应物资总需求量;式(14)为调度到需求点j的w类型物资量与其需求量相等。
2.4 算法设计
遗传算法具有模仿自然界的选择与遗传机理寻找最优解的特性。先将问题参数编码为染色体,再利用迭代的方式进行全局寻优,最终生成符合优化目标的染色体。[18]在一次完整的应急物资调度过程中,参加调度任务的所有船舶的调度任务序列为1条染色体,任意1艘船舶的全部调度任务为1个基因,任意1艘船舶的单次完整调度任务为1个基因单元。本文的研究模型采用符号编码形式,定义如下:
Sn为第n个应急储备库;Dn为第n个物资需求点;w1、w2和w3分别为阻拦类物资、回收类物资和其他物资;cA和cB为应急物资运输船舶A和应急物资运输船舶B。
A船为港作拖船,B船为港口运输货船,cA={300,8,u},cB={100,20,v}。即A船和B船的载货量分别为300 t和100 t,满载航行速度分别为8 n/h,20 n/h。A船序号为u(u=1,2,…,k),B船序号为v(v=k+1,k+1,…,g)。
建立遗传算法的基本步骤示意见图2。
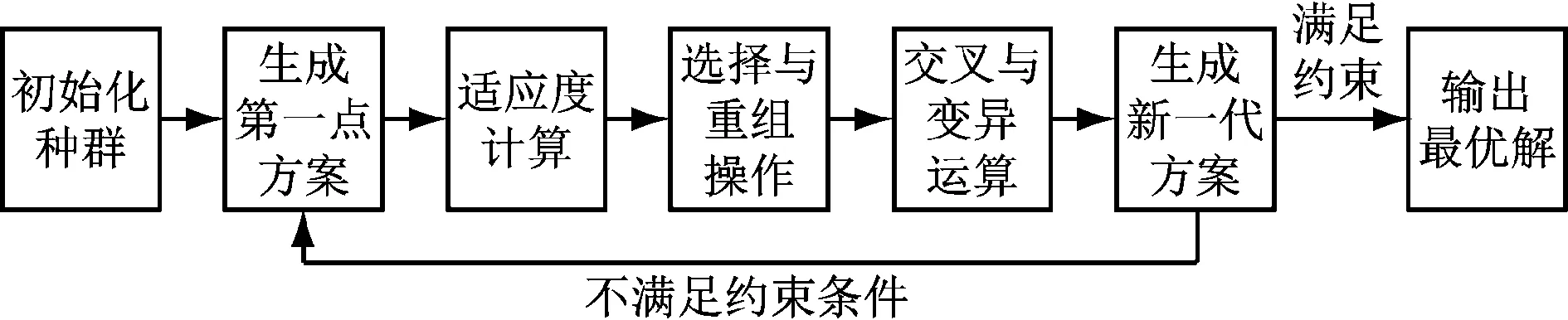
图2 遗传算法的基本步骤示意
3 算例分析
为验证模型的有效性,假设某水域发生船舶溢油事故,事故点坐标为北纬41.178 5°,西经72.548 1°,溢油量500 t,风向SW,风速4 m/s。先通过溢油仿真判断物资需求点位置,再结合应急物资储备库信息求解应急物资调度船舶的调度方案。
3.1 溢油预测分析
根据第2.1节,利用GNOME软件仿真[19],软件中溢油点位置和溢油量等信息设置情况见图3;初始事故点的风向和潮流等信息的设置情况见图4;船舶溢油事故点24 h之后的溢油预测位置见图5。

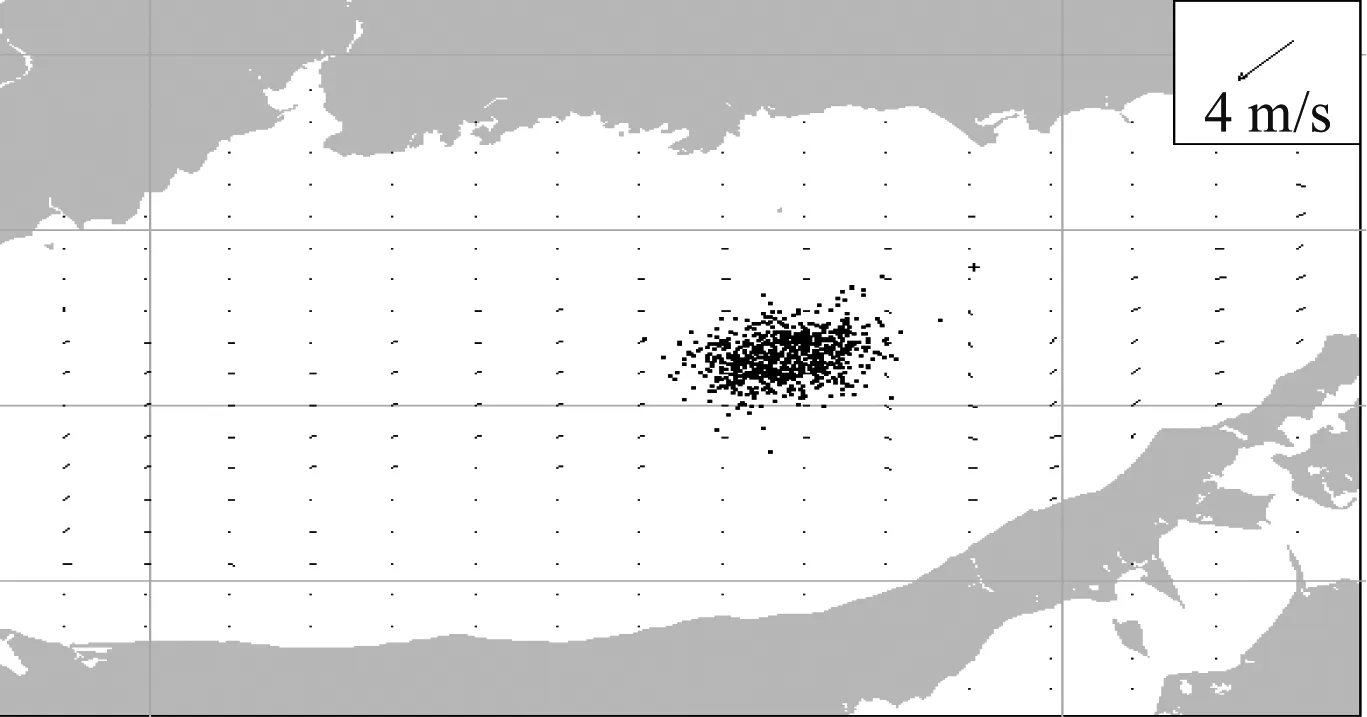
图5 船舶溢油事故点24 h后漂移位置预测
通过软件仿真可得溢油经历24 h漂移之后的位置,基于该仿真结果可确定2个应急物资需求点的位置。溢油工作船舶基于这2个需求点展开溢油的回收与围控。应急物资运输船循环往返于应急储备库与物资需求点之间,开展相关应急物资的运输。
通过类比同类型溢油事故,得到此次溢油事故各应急物资需求区间的估值结果见表1。利用第2.2节三角模糊数理论进行处理,得出3种应急物资的具体需求量。
3.2 多物资调度方案确定
通过提取事故特征,结合调研信息,给出此次事故的应急储备库的名称、配船类别和编号,见表2;应急储备库各物资储备与处理之后需求点各物资具体需求量见表3;应急储备库与其需求点之间的距离见表4。

表1 需求点物资需求区间 t

表2 应急储备库的名称、配船类别和编号
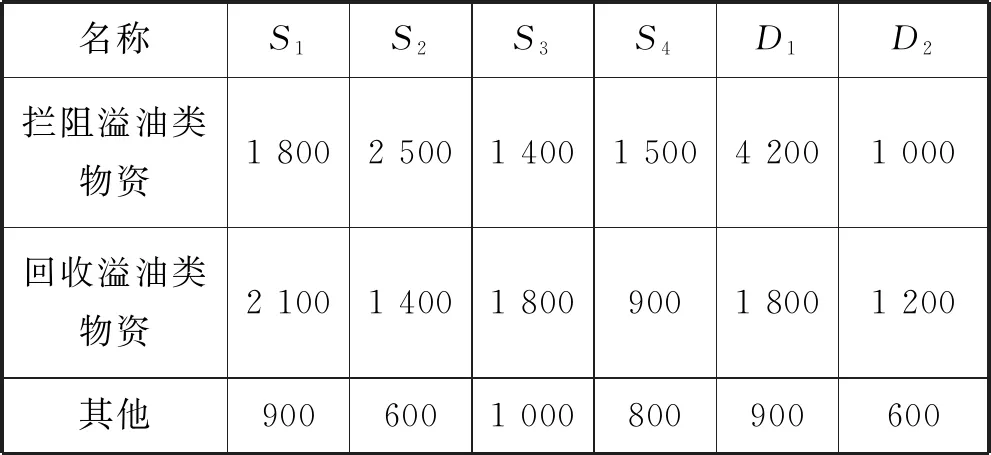
表3 应急储备库储备量与处理后需求点各物资需求量 t
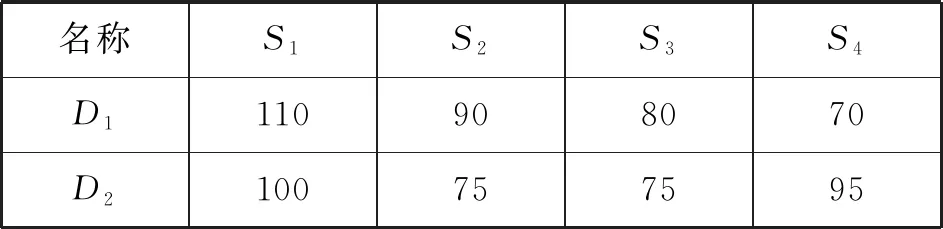
表4 应急储备库与其需求点之间的距离 n mile
遗传算法作为启发式算法,易陷入局部收敛,出现局部最优解。针对遗传算法的不足,在遍历状态过程中,从50次较优解中选择配送时间最短的解作为最优解。最优解对应的染色体可确定最终调度方案。调度任务完成时间与迭代次数的关系见图6和图7。经2 000次迭代和10 000代得到的结果相同,对应的配送时间Y=66.5 h。根据最优解条件下的染色体信息确定调度方案,见表5和表6。
由表6可知:最优解下的调度方案满足应急物资储备库与需求点3种类型物资的供需关系,通过比较2种调度方案可得11号船舶的配送时间最长。

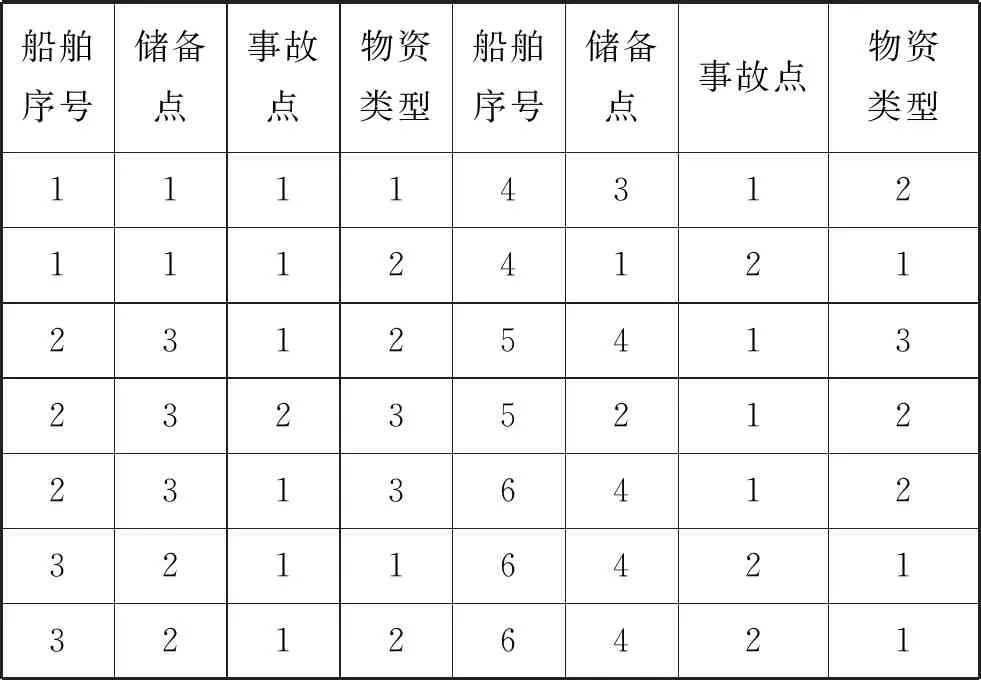
表5 A类船舶调度方案
考虑往返,完成调度总时间为66.5 h,与算法迭代时间相同。通过验证到达各物资点的应急需求量,发现调度方案能满足需求,验证该方案是可靠的。通过比较以往对海上船舶溢油事故的研究[20-22],本文提出的多应急物资需求、多船舶特征下的调度更能与实际相符。
4 结束语
海上船舶溢油事故具有持续性和漂移扩散性,本文研究多应急物资、多调度船舶下的溢油应急物资调度问题。先通过GNOME软件仿真确定漂移扩散位置,再确定物资需求点,随后利用三角模糊数方法确定在模糊状态下的应急物资需求量,最后构建针对海上船舶溢油事故的应急物资调度模型。模型的运用需事先明确应急储备库储备、可调度船舶数量、应急储备库与事故点距离等信息。模型解决了应急物资储备库对各种物资的调度分配问题。此外,本文没有考虑船舶溢油事故发生时所需应急物资需求的优先级问题,未考虑不同物资装卸时间的问题,需在今后的研究中进一步改进。
