基于氧气A波段发射谱线临近空间大气温度的反演及分析

杨晓君，王后茂, 李叶飞，王咏梅，胡秀清

1. 中国科学院国家空间科学中心, 空间环境探测研究室，北京 100190 2. 天基空间环境探测北京市重点实验室，北京 100190 3. 中国科学院空间环境态势感知技术重点实验室，北京 100190 4. 中国科学院大学天文与空间科学学院，北京 100049 5. 上海卫星工程研究所，上海 200240 6. 中国气象局国家卫星气象中心，北京 100081

引 言

地球大气临近空间区域的物理和化学特性研究需要准确的了解该区域的温度分布，在临近空间区域发生的许多过程都具有明显的温度依赖性。此外，临近空间大气参数很大程度上也影响着空间天气预报以及航天器发射与再入轨过程的安全性预估等[1]，因此对临近空间大气的观测与研究具有重要的科学意义和应用价值。虽然火箭和地面测量已经可以获得准确的温度廓线，但很难用它们建立一个全球的温度分布数据库，星载探测可以在较短时间内进行全球或者区域的大范围观测。美国空间物理研究实验室基于搭载在URAS卫星上的高分辨率多普勒成像仪HRDI(The high-resolution Doppler imager)通过观测氧气A波段的发射谱线进行温度的测量[2], 采用基于扰动理论的最优估计法对80～100 km高度的大气进行反演，利用三条谱线协同反演得到误差约为7 K的温度廓线，首次提供了该高度范围全球温度测量结果。之后, 2001年搭载在TIMED卫星上的TIDI(TIMED Doppler Interferometer)多普勒成像仪基于氧气A波段发射谱线对60～300 km高度的临近空间大气温度进行了遥感观测，基于谱线的观测值采用约束非线性最小二乘拟合得到温度廓线[3]。2001年2月20日，搭载在Odin卫星上的光谱仪和红外成像系统OSIRIS(optical spectrograph and infraRed imaging system)对氧气A带的发射光谱进行了探测，将90～110 km内的氧气A波段光谱与模拟光谱进行逐像素比较，用最小二乘法使波段谱差的平方和最小，从而得到中层-低热层区域的温度，在90 km附近的温度反演精度约为±2 K，在较高高度的精度为±6 K[4]。先进地球观测卫星ADEOS上搭载的大气光谱仪ILAS测量了包括以762 nm为中心的分子氧A波段在内的753～784 nm波段的大气吸收光谱，通过卫星太阳掩星对氧气A波段吸收光谱的测量，采用层析法获得了整个平流层的温度分布[5]，与仪器功能相关的误差是系统不确定性中最大的误差源, 与所考虑的系统不确定性相关的温度的均方根误差估计为4 K。全球高分辨率热层成像迈克尔逊干涉仪MIGHTI(Michelson Interferometer for Global High-resolution Thermospheric Imaging)搭载在NASA的电离层连接探测器ICON上于2019年10月11日发射[6]，MIGHTI被用来测量地球热层的中性温度[7]，反演方法是使用离散波长测量A波段的光谱形状，从波段的旋转包络线推断出环境温度，在白天90～105 km之间的测量精度为1K，而在夜间，测量精度在90 km时为1 K，在105 km时增加到了3 K[8]。

以上仪器选取的谱线都不同，而影响反演结果非常重要的一点就是谱线的选择。我们在氧气A带所有谱线中对比不同谱线特性，寻找谱线选择的判断条件，然后选取合适的谱线基于最优估计的方法进行温度的反演，并进一步探讨了谱线线强对反演结果的影响。

1 正演模型

产生氧气A波段的激发态氧气分子是由一系列复杂的光化学反应产生的，当激发态氧气分子自发辐射产生氧气A波段时会发出光子，波数ν处的特定转动谱线发出的光子数可以表示为fDη，D是多普勒线型，η是体发射率，f是谱线强度，是温度的函数

(1)

式(1)中，fref是在参考温度Tref=296°K时的谱线强度，E′是转动谱线的上能级能量。式(2)是以vc为谱线中心的多普勒线型

(2)

(3)

其中，k是玻尔兹曼常数，c是光速，m是氧气分子量。

综上所述，卫星观测到的光谱亮度可以从切点高度Zt沿视线进行路径积分得到

(4)

其中，s是视线路径，n为氧气数密度，σ为吸收截面。由式(4)可得，光谱辐射主要由氧气体发射率和温度决定，而光谱辐射对温度的依赖主要是通过自吸收截面等的作用[9]。

为了更真实的模拟星载测量，引入仪器函数，因此模拟的仪器计数值用式(5)获得

(5)

式(5)中，I为卷积的归一化仪器函数，是半高宽(FWHM)为20 cm-1的高斯函数。

2 反演模型

2.1 扰动理论

卫星的观测结果可表示为

C=KT+ε

(6)

式(6)中，C是卫星观测的辐射强度向量；T是待反演的温度向量；K是描述大气物理过程正演模型的权函数矩阵；ε是测量误差向量。

首先，分别模拟临边辐射强度测量值和用体发射率廓线、温度廓线初值计算得到的正演模型值。模拟过程中的谱线线强、上能级能量等参数均来自2004年的HITRAN光谱数据库[10]，而大气分子浓度和温度廓线数据均来自MISIS-00模型[11]，体发射率廓线是由光化学模型利用温度各组分数密度廓线计算得到[12]。测量值Cmeans和用初始温度、体发射率廓线计算得到的正演模型值C00之间的差值可以用线性积分算子表示

本文笔者将微课应用到成人继续教育中，将信息化教学手段融入了传统教学中，从而形成了线上线下的混合式教学模式。这种混合式教学模式是一种优秀的教学模式，它综合了MOOC的优势，弥补了MOOC缺乏管理机制的缺陷，利用现有大量的MOOC资源，降低了微课制作的工作量，突现了“互联网+”时代的优势。

(7)

其中z为切点高度(km)； 矩阵中C和T下标为视线切点高度(km)； 矩阵K下标为所在行视线积分的高度和依次改变温度值所对应的高度； ΔT=Ttrue-T00为真实温度值与初始温度值的差值；Cmeans是输入温度为T00+ΔT的模拟值；C00是输入温度为T00的模拟值。

以1 km为格点对温度廓线加入扰动，每改变一个格点就产生一条新的扰动廓线ΔT/T00，51条廓线就可以用ΔT/T00组成的矢量Tf来表示。为了得到更高的精确度，式(7)中的积分与正演模型中的一样，积分步长都为1 km。将模拟临边扫描的所有测量计数值作为C矢量，这样就得到了一个矩阵方程ΔC=KTf用来求解未知量Tf。

2.2 反演算法

理论上，温度可以直接利用氧气A波段的观测辐射光谱通过求解辐射传输方程来获得，然而事实上求解这一方程是不可能的，这主要是因为其解是不唯一且不稳定的； 同时由于观测误差的存在，使得简单的单步反演法在实际应用时容易导致较大的反演误差，抗干扰能力比较低。基于贝叶斯理论的最优估计法是一种求解有噪声反演问题的非常好的手段，用实时探测数据替代非待反演参数，并利用先验信息对反演结果进行约束和修正，得到待反演参数最合理的解，提高了反演精度和抗干扰能力。

在2.1扰动理论的基础上，选择了基于贝叶斯理论的最优估计法进行温度的反演。假定测量误差和先验信息误差服从高斯分布，将求解辐射传输方程转化为使概率函数最大化的最优化数学问题，求解这个概率问题就可以获得温度的最优解。

将T看做一个多维随机变量，其概率密度函数为

(8)

条件概率密度函数可表示为

(9)

其中，Sa是描述T0不确定性的先验信息误差协方差矩阵； 对角矩阵Sε是从观测值得到的测量噪声协方差矩阵，是描述C和正演模型不确定性的观测误差协方差矩阵。假设测量误差的总体方差和探测器上的计数值一样服从泊松分布。先验估计协方差矩阵Sa可以模拟为

Sa=αTJ

(10)

式(10)中，z是反演的网格高度，αT=103K2。先验估计协方差矩阵表示了一个预期的均方根变化约为5%(～10 K)的先验温度廓线。

根据贝叶斯定理，最有可能的大气状态剖面是使式(11)最大化[13]

P(Tf|C)=P(Tf)P(C|Tf)/P(C)

(11)

其中，P(Tf)是温度参数分数变化的先验概率分布；P(C)观测数据的先验概率分布，其为常数；P(C|Tf)给定温度参数分数变化条件下具体观测数据的似然概率；P(Tf|C)是组合先验信息和似然概率得到的温度参数分数变化后验概率。

将式(8)和式(9)相乘，最有可能的T值是质式(12)最小化

(12)

式(12)最小化时的T的估计值为

(13)

其中，T0=0, 所以方程可化为

(14)

再由Test求得温度廓线的最优估计值Ttrue。

3 反演结果及讨论

3.1 正演模型

为了验证上述反演方法的可行性和精确度，利用构建的正演模型来模拟实测值进行温度的反演研究。首先利用一组温度输入值T00作为初始值来获得一组正演模拟值，然后在T00的基础上加上一组随机温度变量得到新的温度廓线Ttrue=T00+ΔT，再由新的温度廓线模拟一组实测辐射值，最后由该两组辐射模拟测量值组合进行温度反演，将反演得到的结果与初始温度输入值进行比较。图1就是正演模型所用的温度廓线初始值(T00)和模拟的实际测量值所用的温度廓线(即温度真实值：Ttrue)。

图1 温度廓线初始值和实际测量值对比

3.2 无噪声时的反演结果分析

基于HITRAN数据库中氧气A带(759～767 nm)内包含的几十条谱线参数，我们将所有的谱线进行了辐射模拟与温度反演分析，结果表明不同谱线的反演结果精度不同，精度较好的谱线主要集中在759～760和764～766 nm这两个波段范围，图2为氧气A带中无噪声情况下60～110 km范围内的温度反演精度较高的谱线。如图2所示，ΔT=Ttrue-T00为真实温度值与初始温度值的差值，其他折线为利用不同谱线反演ΔT的结果，17条氧气A波段的温度反演结果在60～110 km高度范围内效果较好，平均反演偏差为4.1 K。

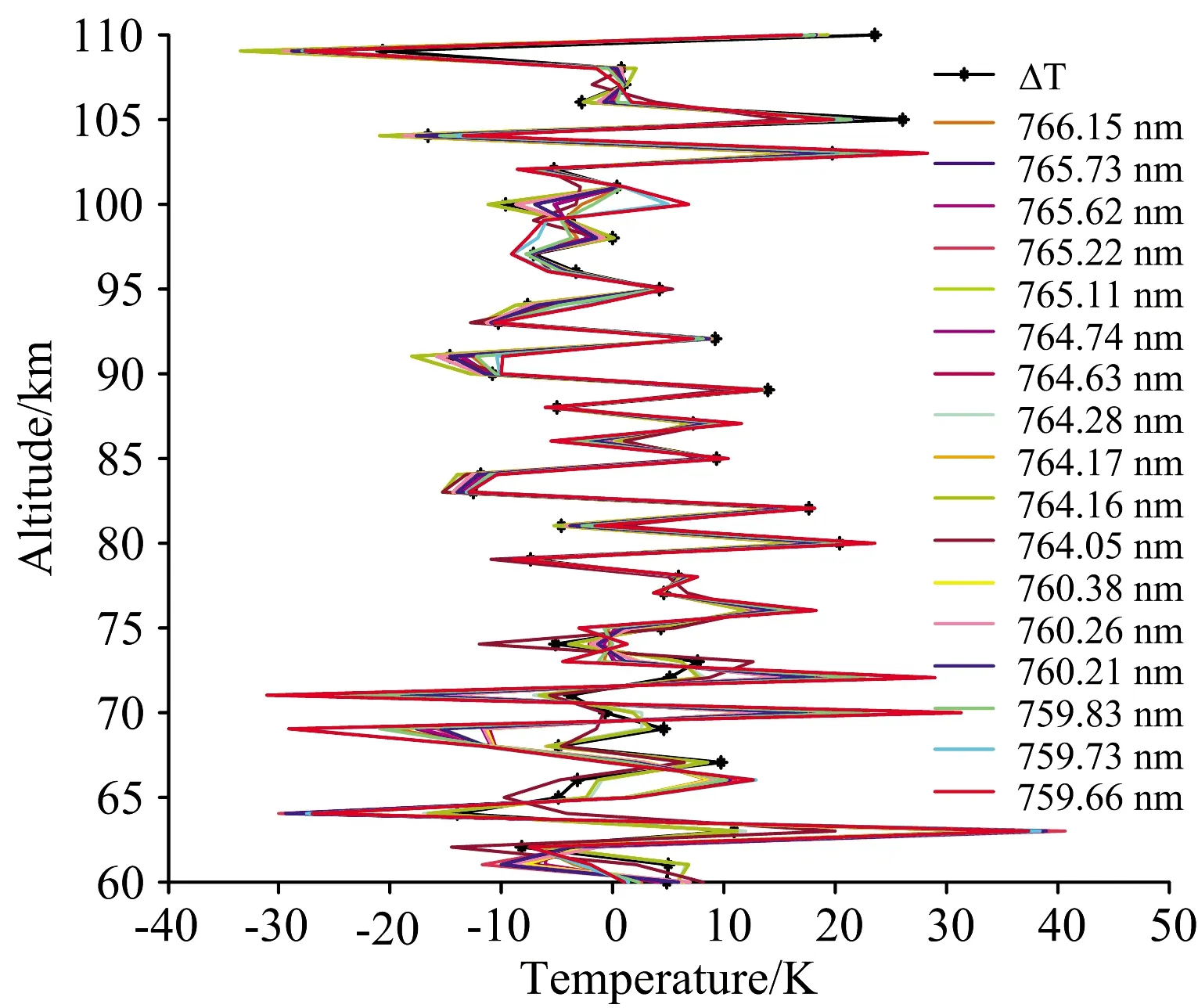
图2 无噪声条件下谱线在60～110 km范围内的 温度反演结果对比

但有些谱线的反演误差在80 km以上较小，80 km以下却较大，如图3所示，764.28和764.17 nm为图2中反演精度较高的谱线，另外两条为反演精度较差的谱线(761.72和761.25 nm)。将他们的反演结果进行进一步的对比分析，如图3所示，80 km以上四条谱线显示了较好的反演精度，平均反演误差<5 K； 而在80 km以下，761.72和761.25 nm的反演结果与真实值存在较大的偏差，平均偏差达到了34.9 K。原因如下： 由式(4)可以看出，温度通过影响线强和自吸收两部分来影响辐射强度，且温度对它们的影响正好相反，权函数就是用来表示温度对辐射强度影响大小的，而反演结果的差距可从其权函数中得到规律。图4为两条谱线761.25和764.28 nm的权函数，为方便对比各选取一条代表线标记为红色(71和80 km)，图中每一点代表的都是对应高度处的温度变动对卫星辐射强度观测的影响与温度的扰动量的比值，即ΔC/ΔT，温度扰动ΔT设置为5 K，由图4(a)可以看出，当温度对自吸收的影响所占比重大于对线强的影响时，ΔC/ΔT会发生正负翻转，反演精度会变差； 从图4(b)可以看出，影响因素占主导地位的是线强，温度主要通过对线强的影响来改变辐射强度，其对自吸收的影响比重较小，ΔC/ΔT未发生正负翻转，反演效果比较好。同时，我们将其他谱线的反演结果进行比较得出相同的结论，因此可以根据这个规律，从氧气A波段众多谱线中筛选适合用于温度反演的谱线，即温度对自吸收影响相对较小的谱线。

图3 无噪声条件下四条谱线在60～110 km范围内的 温度反演结果对比

图4 权函数矩阵Fig.4 Weight function matrix

3.3 添加噪声后的反演结果分析

在实际的观测中，除了上述考虑的因素外，还需要考虑信噪比的影响。因此，本文将图3中的四条谱线模拟值加入随机噪声并进行了反演及结果分析，结果如图5所示。764.28和764.17 nm两条谱线的反演结果与真实值基本吻合，说明噪声对这两条谱线的影响非常小，该谱线的辐射强度能够满足温度反演的要求。而761.72和761.25 nm这两条谱线在80 km以下的反演偏差变得更大，最大偏差达到几百K，原因是这两条谱线本身在80 km以下反演误差就非常大，微小扰动就会造成较大的误差，所以加入噪声后使得反演偏差变得更大。

图5 加入噪声情况下四条谱线在60～110 km范围内的温度反演误差

为了进一步分析噪声对反演结果的影响，本文选择了四条较强谱线和一条弱谱线，如表1所示，其中762.2 nm为弱线，反演结果如图6所示。图6是762.2 nm无噪声情况和加入噪声时的反演结果比较，蓝线为无噪声情况下的结果，红线为加入噪声的结果。无噪声情况下，弱线762.2 nm与强线764.28和764.17 nm的反演结果相对一致且都比较好； 加入噪声后，由于本身辐射强度弱，所以信噪比低，反演效果变得比较差。原因是弱线容易受噪声的干扰，抗干扰能力低。因此，谱线选择时，线强也是另一个重要的判断依据，强线更有利于提高反演精度。

表1 模型中用到的谱线参数Table 1 Constants of rotational lines of model

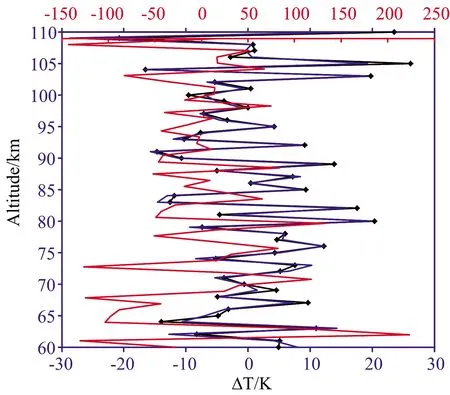
图6 谱线762.2 nm在无噪声情况和加入噪声时60～110 km范围内的温度反演误差

为了进一步确定线强对反演结果的影响，我们选择通过增加线强的方式进行反演精度分析，图7为分别将线强增加1～5个量级后得到的反演结果。由图可得，80 km以上，随着线强量级的增大，反演精度增加，反演结果更接近初始输入值； 线强增加三个量级时，反演精度可以达到5 K。由此得出： 弱线762.2 nm在信噪比足够大，也就是线强达到10-26的量级时，也可用来反演80 km以上的温度并获得精确的反演结果。

图7 增加谱线762.2 nm线强量级对反演结果的影响

4 结 论

在临近空间大气温度反演中，不同的谱线反演精度不同，基于贝叶斯反演理论选取了不同的谱线进行一系列反演试验及结果分析，并基于权函数和谱线线强与反演精度差异的关系进行了分析。

具体结果如下：

(1)当温度对自吸收的影响所占比重大于对线强的影响时，权函数会发生正负翻转，反演精度变差，原因是自吸收降低了辐射强度对温度的灵敏度，因此，权函数变化规律可以作为谱线选择的判断依据。

(2)在有噪声的情况下，强线比弱线的抗干扰能力更强，反演精度较高，更适合用于温度的反演，所以线强也是谱线选择的另一个重要的依据。根据分析结果，当谱线线强达到10-26的量级时，谱线的辐射强度较强，此时谱线可用于80 km以上的温度反演。