C.I.分散棕19在超临界CO2及水中溶解性的分子动力学模拟
2021-01-05王纯怡毛志平
王纯怡, 吴 伟, 王 健, 徐 红,4, 毛志平,4,5
(1. 东华大学 生态纺织教育部重点实验室, 上海 201620; 2. 东华大学 化学化工与生物工程学院, 上海 201620;3. 青岛即发集团股份有限公司, 山东 青岛 266000; 4. 东华大学 纺织科技创新中心, 上海 201620;5. 上海安诺其集团股份有限公司, 上海 201703)
超临界CO2染色是近年来发展起来的一种新型高效环保的染色技术,相比于传统水染技术拥有许多优点[1]。分散染料作为在超临界CO2染色技术中应用最广的染料,其溶解度已被广泛研究。分散染料在超临界CO2中的溶解度对于染色过程中的染料筛选,染色效果的提高以及染色系统参数优化等方面均具有重要影响[2]。分散染料的相对分子质量较小、分子极性低,CO2分子是非极性分子,根据“相似相溶”原理,一般认为分散染料可较好地溶解于超临界CO2中[3]。目前,研究人员已开发设计出多种分散染料在超临界CO2中溶解度的测定方法和设备,用于测定高温高压下分散染料在超临界CO2中的溶解度以及影响溶解度的因素[4]。基于方法与设备的成熟,分散染料在超临界CO2流体中的溶解度数据近年来已经有了比较充分的记载。尽管分散染料溶解度能够随着体系温度和压力的变化而变化,但是研究表明,在超临界CO2中,所测试的所有分散染料溶解度都较低[5]。在常规染色压力和温度下,分散染料在超临界CO2中的溶解度仅在1×10-9~1×10-5mol/mol范围内[6-8],并且,溶解度测定方法始终没有统一的标准,不同文献报道中的同种分散染料溶解度数据通常存在较大差异[6,9]。
分散染料分子结构中几乎不含水溶性基团,因此其在水中的溶解性较低。有研究表明,即使在最高染色温度下,分散染料在水中溶解度也一般不超过100 mg/L[10],因此准确测量分散染料在水中的溶解度一直是一大难题。大多关于分散染料在水中溶解度的测定实验都是30年前进行的,且均以过滤技术为基础[11-12]。如今,商品化加工使得分散染料的粒径不断减小,传统过滤技术也越来越不受用。由于染色过程中分散染料通常需要以悬浮液的形式稳定分散在溶液中,因此分散稳定性是评价分散染料性能的重要指标[13],相对而言,分散染料在水中的溶解度研究范围明显较小。受限于实验条件以及研究范围,分散染料在水中溶解度的研究成果较少。
近年来,由于科学技术的发展,分子动力学模拟方法逐渐成为科学研究中的重要手段。基于分子动力学模拟研究发色液晶材料中的染料分子聚集[14]以及溶质分子在不同溶剂中的溶解行为[15]等已逐渐普遍。分子动力学模拟能够从微观尺度研究体系的物理化学行为,简单高效且成本低廉。
本文基于分子动力学模拟的方法,分别研究了C.I.分散棕19染料在超临界CO2和水中的溶解性。通过计算C.I.分散棕19染料在超临界CO2及水中的自由能,并分析染料分子与超临界CO2分子及水分子间的弱相互作用,从而探究了分散染料在2种溶剂中的溶解性大小,并从微观角度分析染料在不同溶剂中溶解性差异的原因。这对于在一定程度上弥补实验方法缺陷,研究同种分散染料在超临界CO2及水中的溶解性,进而探索分散染料溶解性研究的新方法,合理筛选不同染色方法用分散染料,完善分散染料的染色工艺,均具有重要的理论指导意义。
1 分子动力学模拟
1.1 模型及力场的选择
本文研究选用Gromacs(版本2018.2)程序进行模拟研究。分散染料分子选用OPLS-AA (optimized potentials for liquid simulation-all atoms)[16]力场,超临界CO2分子选用EPM2 (elementary physical model)[17]模型。水分子选用了TIP4P水模型。力场与模型的选择是基于许多已发表研究而确定的[18]。
本文研究模拟选用的染料为C.I.分散棕19,其分子结构式如图1所示。
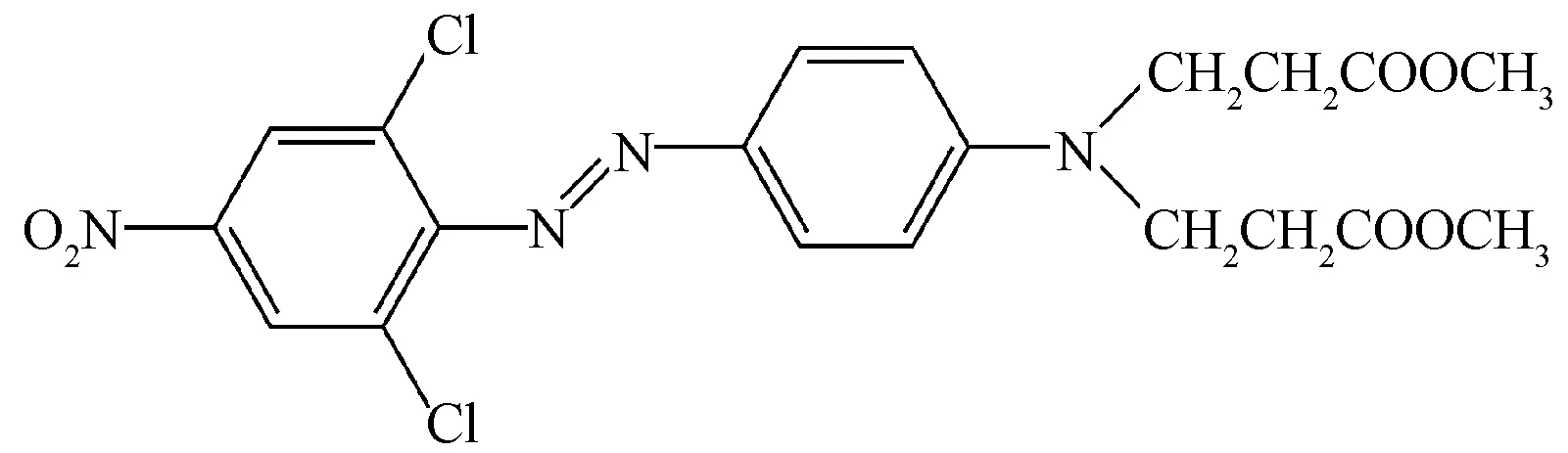
图1 C.I.分散棕19化学结构式Fig.1 Chemical structure of C.I. Disperse Brown 19
如图1所示,C.I.分散棕19是一类偶氮染料,对于所使用的OPLS-AA力场,偶氮参数是缺失的,因此,基于Pipolo等[19]的研究成果可为染料分子偶氮部分的相关原子重新定义合适的力场参数。除此之外,有研究表明OPLS-AA力场更适合与1.2×CM5电荷联用,这样能够使模拟结果更精确[20],因此,本文中染料分子的电荷使用的是1.2×CM5电荷。具体计算方法为:首先,使用ORCA 4.1.0程序以及B3LYP/6-311G**方法优化染料分子结构,然后将优化后所得到的波函数信息导入到Multiwfn(版本3.6)程序中进行染料分子CM5电荷的计算,最后再乘以1.2就可作为染料分子的电荷。
1.2 自由能计算
1.2.1 自由能模型的构建
基于分子动力学模拟方法计算染料分子在超临界CO2及水中的溶解自由能以及结合自由能,可分析在2种溶剂染色条件下染料的溶解情况以及染料分子间的聚集情况。其中,每种溶剂的研究均包含两部分模拟:一是染料分子在溶剂中的耦合(溶解自由能);二是染料分子与染料分子的耦合[21]。为此,设置了4个模拟体系,包括1个染料分子分别在超临界CO2及水中的模拟,2个染料分子分别在超临界CO2及水中的模拟。模拟体系的具体设置如表1所示,初始构型如图2所示。
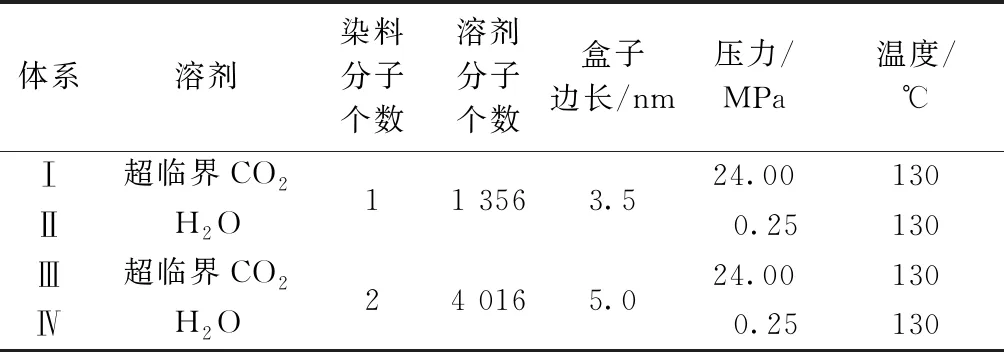
表1 自由能计算的模拟设定Tab.1 Simulation settings for free energy calculations
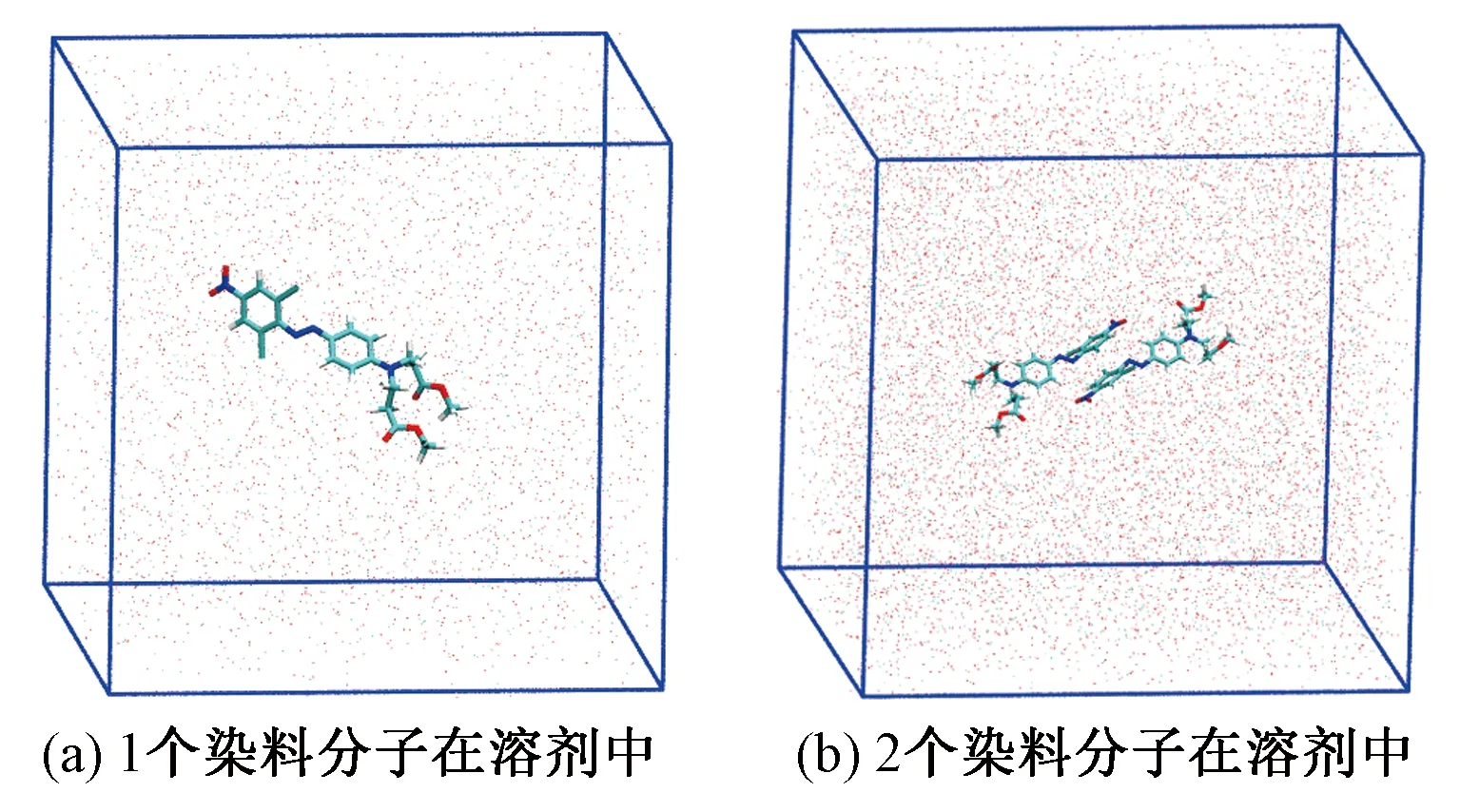
图2 自由能计算的初始构型Fig.2 Initial configurations for free energy calculations.(a)One dye molecule in solvent; (b) Two dye molecules in solvent
1.2.2 自由能模拟细节
在计算自由能的模拟过程中,通过对参数文件的设置可慢慢打开染料分子与周围环境的相互作用,打开前后体系自由能变化即为所得。在此过程中,需要先打开范德华力,再打开静电力。无论是范德华相互作用的耦合,还是库仑相互作用的耦合,都线性依赖于控制系统状态的参数λ,其中,λ为0表示相互作用完全关闭,λ为1表示相互作用完全打开,从0到1设置不同间距的λ可控制相互作用打开得快慢,这关系着计算量的大小以及计算结果的准确性[22]。本文研究中,λ具体设置为:范德华相互作用打开过程λ为0.0、 0.2、 0.4、 0.5、 0.6、 0.7、 0.8、 0.85、 0.9、0.95、0.97、0.99、 1.0、 1.0、 1.0、1.0、 1.0、 1.0、 1.0、 1.0、 1.0;静电相互作用打开过程λ为0.0、 0.0、 0.0、0.0、0.0、 0.0、 0.0、 0.0、0.0、 0.0、 0.0、 0.0、 0.0、 0.2、 0.4、 0.5、 0.6、 0.7、 0.8、 0.9、 1.0。对于每个λ都需要进行1次独立的模拟过程,包括能量最小化、预平衡模拟(NVT、NPT)以及成品模拟(MD)过程,因此,对于每个模拟体系的每1遍模拟,都需要进行21次模拟过程。为了保证计算结果的可信度,每个模拟体系重复进行了3遍。
对于所有模拟过程,库仑相互作用和范德华相互作用均采用Particle mesh Ewald(PME)方法计算,截断半径均为1.0 nm。 牛顿方程采用随机跳跃积分方法进行积分,时间步长为2 fs。周期性边界条件被用于所有方向。首先,采用最陡下降法对体系进行能量最小化模拟。然后进行100 ps的NVT预平衡模拟,接着进行100 ps的NPT预平衡模拟。为了防止染料分子在体系中乱跑,阻碍收敛,在NVT、NPT模拟期间引入了限制势[23]。最后,进行6 ns恒温恒压的MD模拟。在模拟过程中,所有的键都采用Lincs算法进行约束。模拟完成后的分析基于Klimovich等提出的Python工具alchemical-analysis[24]进行,其可自动调用不同方法进行自由能计算,本文研究中调用了热力学积分方法来计算最终的自由能。
1.3 弱相互作用分析
1.3.1 弱相互作用模型的构建
本文研究采用平均非键相互作用(aNCI)[25]方法分别研究染料单分子与超临界CO2分子及水分子间的弱相互作用。其中,压力和温度的设置与1.2.1节相同,都是按照染色条件设置的。模拟体系的具体设置如表2所示,初始构型如图3所示。

表2 弱相互作用分析的模拟设定Tab.2 Simulation settings for analysis of weak interactions
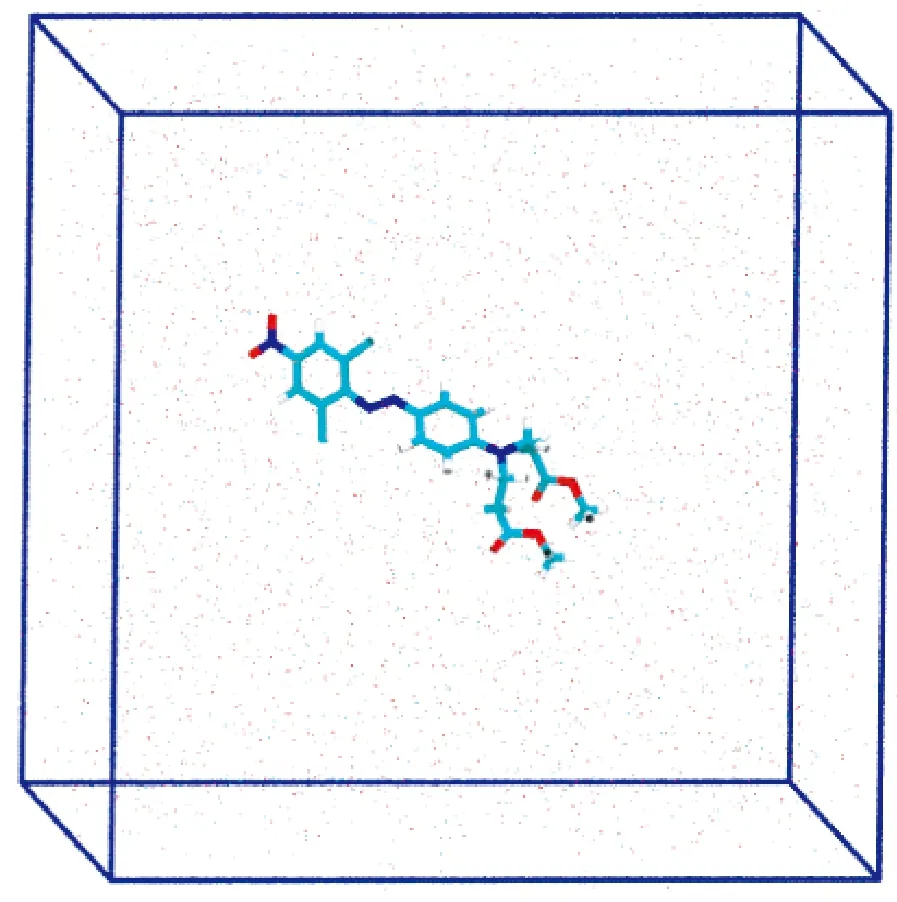
图3 弱相互作用分析的初始构型Fig.3 Initial configuration for the analysis of weak interactions
需要特别注意的是,对于染料分子在进行动力学模拟之前,其坐标都将保持冻结,即将染料分子固定在模拟盒子中间,模拟过程中只有周围的CO2分子或水分子在不停运动,而染料分子保持不动。
1.3.2 弱相互作用模拟细节
对于本文所有模拟体系,库仑相互作用均采用PME方法计算,截断半径为1.5 nm,范德华相互作用采用Cut-off方法计算,截断半径也为1.5 nm。牛顿方程采用蛙跳算法进行积分,时间步长为1 fs。周期性边界条件被用于所有方向。首先,采用最陡下降法对体系进行能量最小化模拟。然后进行100 ps的NVT预平衡模拟,接着进行10 ns的NPT平衡模拟。NPT模拟完成后可得到含有2 001帧轨迹的坐标文件,将其导入Multiwfn程序中进行弱相互作用分析,Multiwfn会计算每1帧的电子密度及其梯度和Hessian,并取平均,之后用平均量计算出平均的NCI。最后计算得到的文件用VMD打开并经过适当的处理,染料分子与周围分子间的弱相互作用就可以被图形化展示出,同时得到的还有展示其弱相互作用稳定性的热波动指数(thermal fluctuation index, TFI)。在模拟过程中,所有的键都采用Lincs算法进行约束。模拟完成后的分析都是基于Gromacs程序以及图形显示程序VMD(版本1.9.3)进行的。
2 结果与分析
2.1 C.I.分散棕19在溶剂中的自由能
从微观角度来说,分散染料在溶剂中的溶解性体现在2个方面:一是染料分子与溶剂分子间的作用,二是染料分子与染料分子间的作用。因此,自由能的计算也包括2个方面:一个是ΔGsol,代表染料在溶剂中的溶解自由能;另一个是ΔGbind,代表2个染料分子在溶剂中的结合自由能,能够反映染料在溶剂中的聚集倾向。其中,ΔGsol为染料分子在溶剂中解耦合前后得到的自由能变化值,而ΔGbind为染料分子与染料分子间解耦合前后的自由能变化值与ΔGsol的差值[21]。
表3中示出基于分子动力学模拟,使用热力学积分方法计算得到的C.I.分散棕19染料在超临界CO2(24 MPa,130 ℃)及水(0.25 MPa,130 ℃)中的溶解自由能ΔGsol和结合自由能ΔGbind。如表3所示,对于同种溶剂,ΔGsol以及ΔGbind均重复计算了3次。可以看出,3次重复计算的结果差异不大。染料在2种溶剂中的溶解自由能和结合自由能绝对值均较小,且大致相当,说明C.I.分散棕19在2种溶剂中的溶解性均不佳,且相差不大;但是相比于水,染料在超临界CO2中的溶解自由能绝对值稍小,结合自由能绝对值稍大,说明在染色条件下,C.I.分散棕19染料在超临界CO2中的溶解能力稍差,且染料分子更倾向于分子间的聚集。自由能计算结果说明了在各自染色条件下,C.I.分散棕19染料在超临界CO2和水中溶解性相当,但是在超临界CO2中稍差一些。
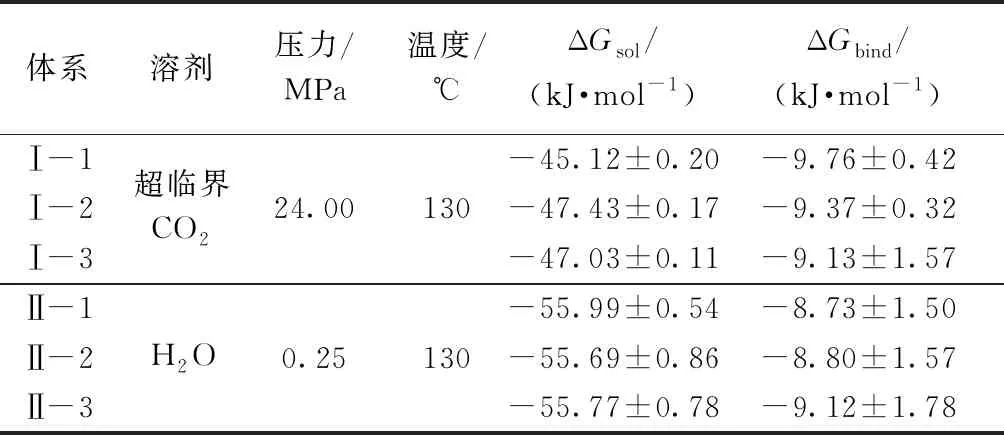
表3 C.I.分散棕19在超临界CO2及水中的自由能Tab.3 Free energies of C.I. Disperse Brown 19 in supercritical CO2 and water
2.2 C.I.分散棕19在溶剂中的弱相互作用
aNCI方法分析分子间弱相互作用是基于电子密度、电子密度的梯度以及电子密度的Hessian矩阵的函数用不同颜色投影来实现的,可直观形象地将分子间弱相互作用可视化。与此同时,通过对电子密度方差的计算,可定义热波动指数,通过函数波动大小反映弱相互作用稳定性大小。研究染料分子与超临界CO2分子及水分子在工作条件下的弱相互作用可从分子层面探索染料在2种溶剂中溶解性大小及其差异。
aNCI方法得到的染料分子与溶剂分子间弱相互作用可视化图形的等值面上的不同颜色代表不同类型的相互作用。其中,越蓝的地方说明静电、氢键效应越强,越红的地方说明位阻效应越明显,而绿色表明相应位置平均密度值较低,对应于很弱的作用,即范德华色散作用。图4示出了C.I.分散棕19染料分子与2种溶剂分子在各自染色条件下的弱相互作用类型的图形化分析。如图所示,染料分子与CO2分子和水分子间等值面内外几乎均为绿色,表明染料分子与CO2分子和水分子间的弱相互作用均主要为较弱的范德华色散作用,因而分散染料在2种溶剂中的溶解性均较低。然而从图4(b)可看出,染料分子酯基上的氧原子与水分子间等值面上有极小部分偏红色,表明其中存在微弱的斥力。这可能是导致C.I.分散棕19在超临界CO2体系中溶解性稍差的原因。

图4 C.I.分散棕19在超临界CO2及水中的弱相互作用分析(等值面=0.35)Fig.4 Analysis of weak interactions between C.I. Disperse Brown 19 and supercritical CO2 molecules (a) and water molecules (b) (isosurface of NCI=0.35)
在aNCI方法中,通过计算TFI指数也可得到不同颜色的等值面,反映弱相互作用的稳定性,其中红色到绿色的渐变表示分子间弱相互作用由稳定到不稳定的变化。图5示出了C.I.分散棕19染料分子与2种溶剂在各自染色条件下弱相互作用稳定性的图形化分析。可以看出,当染料分子在超临界CO2中,其等值面内外均为红色,说明了分子间弱相互作用极不稳定(见图5(a));当染料分子在水中, 其等值面外部有大范围的红色,但是
其内部有相当一部分是绿色的,说明虽然其弱相互作用整体上也不稳定,但是相比于超临界CO2,染料分子与水分子间的弱相互作用相对较稳定(见图5(b))。
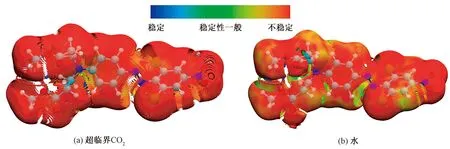
图5 C.I.分散棕19在超临界CO2及水中的弱相互作用稳定性分析(等值面=0.35)Fig.5 Stability of weak interactions between C.I. Disperse Brown 19 and supercritical CO2 molecules (a) and water molecules (b) (isosurface of NCI=0.35)
通过分析染料分子与溶剂分子间的弱相互作用可以看出,C.I.分散棕19染料与超临界CO2分子及水分子间的弱相互作用类型及稳定性相似,均只存在较弱的范德华色散作用,因此其在二者中溶解性相似,且均不佳。相较于在超临界CO2中,染料分子中酯基上的氧原子与水分子间存在微弱的斥力,且其分子间相互作用相对更稳定,因此解释了C.I.分散棕19染料分子在超临界CO2中溶解性更差的原因。
2.3 分散染料在超临界CO2及水中溶解度
为进一步从实验角度验证分子动力学模拟研究结论中C.I.分散棕19在超临界CO2和水中溶解性相当这一重要结论,并验证其对不同分散染料的适用性,表4总结了目前已有文献中报道的多种不同分散染料在2种溶剂中的溶解度数据。为方便比较
分散染料在2种体系中的溶解度大小,染料在水中的溶解度单位由文献中记载的mg/L换算成了mol/mol[26]。在不同体系中,不同分散染料溶解度的测定方法及测定条件均不同,因此溶解度数据大小的对比应考虑较大范围的误差。
从表4可看出,超临界CO2染色在一般压力和温度范围内,不同分散染料的溶解度在1×10-9~1×10-5mol/mol范围内。在水中,在60~90 ℃较高温度下,分散染料溶解度在1×10-8~1×10-6mol/mol;在130 ℃时,溶解度在1×10-7~1×10-6mol/mol范围内,因此,在各自的工作压力温度下,分散染料在超临界CO2及水中的溶解度应该是相当的,只是对于不同的染料,在不同条件下采用不同的测量方法,溶解度值会有所差异。

表4 不同分散染料在超临界CO2和水中的实验溶解度数据Tab.4 Solubilities of different disperse dyes in supercritical CO2 and water
3 结 论
本文基于分子动力学模拟方法,研究了C.I.分散棕19在超临界CO2及水中各自染色条件下的溶解性大小,得到如下结论。
1)C.I.分散棕19染料在超临界CO2和水中的自由能绝对值均较小且相差不大,染料在二者中的溶解性均不佳且大致相当,但是,C.I.分散棕19在超临界CO2中的溶解自由能绝对值稍小于水,结合自由能绝对值稍大于水,说明C.I.分散棕19在超临界CO2中的溶解性比在水中稍差。
2)C.I.分散棕19染料分子与超临界CO2分子和水分子间弱相互作用类型及稳定性相似,均为较弱的范德华色散作用,因此染料在2种溶剂中溶解性均不佳;但是染料分子酯基上的氧原子与水分子间存在微弱的斥力,且染料分子与超临界CO2分子间的弱相互作用更不稳定,导致了C.I.分散棕19染料在超临界CO2中的溶解性稍差。
