露天矿相邻采区间先压帮后留沟内排方式研究
2021-01-05白润才郭伟强刘光伟李浩然徐晋文
白润才,郭伟强,刘光伟,李浩然,徐晋文
(1.辽宁工程技术大学矿业学院,辽宁阜新 123000;2.辽宁工程技术大学煤炭资源安全开采与洁净利用工程研究中心,辽宁阜新 123000)
我国大型露天矿为了使建设初期乃至露天矿的整个服务周期内产生的经济效益最优,通常采用分区开采。相邻采区间合理压帮内排方式的选择就显得尤为重要,方式选择不得当,则会严重影响剥离物运距、运输成本、内排空间、剥采排工程的接续[1-4]。
压帮为露天矿相邻采区间公共端帮处与内排土场之间进行内排。露天矿内排方式根据压帮程度主要有全压帮、半压帮和全留沟3 种方式。全压帮是指压帮高度与开采深度相同,其特点是卡车可进行双翼内排,减小运距,节省运输成本,最大限度的释放内排空间,但二次剥离量多,导致剥离费用高;压帮高度小于开采深度时为半压帮,其特点是有重复剥离量,部分卡车进行双翼内排,部分卡车进行单翼内排。压帮高度等于0 时为全留沟,其特点是完全无重复剥离,但卡车只能进行单环内排,运距增大,且对相邻的采区而言,也无法进行双翼内排,运输成本提高,内排空间利用不充分。
国内学者对露天矿内排留沟与压帮问题的研究不是很多。顾正洪等[5]分析了压帮高度与各技术参数之间的关系,建立了相应的数学模型,并运用相关费用最小法,得出了最佳压帮高度在不同条件下的取值范围;刘光伟等[6]采用费用补偿法确定了最优的压帮高度,并运用最小重复剥采比确定了最优的重复剥离深度;周伟等[7]推导出了计算最佳压帮高度的公式,并分析了最佳内排压帮高度的影响因素;赵俊等[8]建立了全压帮和半压帮内排条件下的重复剥离计算公式和留沟深度的数学模型。
综合上诉分析,专家学者大多对内排压帮高度和重复剥离深度进行了优化研究,对于内排压帮方式研究甚少。针对上述问题,通过对露天矿相邻采区间内排压帮方式进行分析,提出了先压帮后留沟的内排方式,该内排方式结合全压帮与全留沟二者的优点,相比全压帮减少二次剥离费用,相比全留沟减少了运输费用。具体为内排初期先进行全压帮内排,内排土场发展到一定位置时再进行全留沟,采用费用补偿法,证实了该方法的经济合理性,并确定了最优压帮位置。
1 内排运距
露天矿卡车内排时有2 种运输方式,分别为单翼内排和双翼内排。将先压帮后留沟内排方式分为2 个时期,分别为压帮期和留沟期。在压帮期进行的运输方式为双翼内排,在留沟期由于相邻采区公共端帮可以使用,仍然能进行一段时期双翼内排。由于内排土场不断发展,留沟长度越来越大,当双翼内排运距大于单翼内排运距时,运输方式改变为单翼内排。先压帮后留沟内排运距示意图如图1。对留沟期双翼内排转为单翼内排的条件进行分析。采用数学期望法对运距进行计算,即在同一水平下,最长运距与最短运距的平均值为该水平的内排运距[9]。为简化计算过程,取运输重心,并假设采场工作线和剥离工作线相等。

图1 先压帮后留沟内排运距示意图
1.1 压帮期内排运距计算
压帮期内排时,相邻采区公共边帮处能用于卡车运输,采用双翼内排可缩短运距,双翼内排(压帮期)如图1(a)。最长运距(图中I→A→D→F)和最短运距(图中A→D)的平均值为压帮期的双翼内排运距:

式中:L′s 为双翼内排运距,m;L0为采掘或内排工作线长度,m;H 为采深,m;a 为采场与内排土场的坡底距离,m;α 为采掘工作帮坡角,(°);β 为内排工作帮坡角,(°);γ 为端帮(实方)帮坡角,(°)。
1.2 留沟期内排运距计算
留沟期内排分为双翼内排和单翼内排。因此,需分别对其进行计算。
1)双翼内排运距。双翼内排(留沟期)如图1(b)。最长运距(图中J→B→C→D→E)和最短运距(图中A→G)的平均值即为留沟初期的双翼内排运距LS:
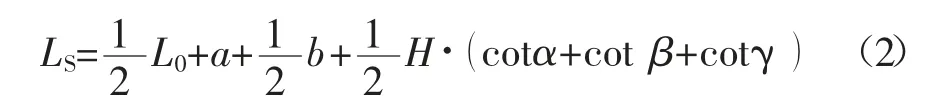
式中:Ls 为双翼内排运距,m;b 为双翼内排留沟期留沟长度,m。
2)单翼内排运距计算。单翼内排(留沟期)如图1(c)。最长运距(图中B→A→D→C)和最短运距(图中A→D)的平均值为留沟期的单翼内排运距LD:

式中:LD为单翼内排运距,m;c 为留沟宽度,m。
当留沟期双翼内排运距大于单翼内排运距时,即LS-LD≥0,整理得:

由式(4)可以得出,影响留沟期内排运输方式转变的变量为留沟长度。当留沟长度大于1 个定值时运输方式由双翼内排转变为单翼内排,此定值由工作线长度、留沟宽度、采深和内排工作帮坡脚共同决定。所以,各露天煤矿需根据其各项开采参数计算求得该矿的最优运输方式转变工程节点。
2 压帮转留沟位置确定
受多种因素影响,大部分露天矿山都面临着排土空间严重紧张的问题[10-11]。因此我国大部分露天矿山很少采用全留沟内排方式。将比较全压帮与先压帮后留沟两种内排方式。将相邻2 个采区命名为Ⅰ区和Ⅱ区。采用费用补偿法,先压帮后留沟方式相对于全压帮方式Ⅰ区和Ⅱ区增加的运输费用与Ⅱ区减少的重复剥离费用和重复剥离运输费用进行综合比较,以此确定先压帮后留沟的经济合理可行性。取采区重心,则采区长度为D,m,压帮长度为X,m;垂直于工作线方向剖面示意图如图2。

图2 垂直于工作线方向剖面示意图
在先压帮后留沟内排方式可行的基础上,随着压帮长度X 的不断变化,增加的运输费用和减少的重复剥离费用都会依次随之改变,那么合理的压帮位置直接影响露天矿先压帮后留沟内排方式的经济效益。
2.1 Ⅰ区增加的运输费用
Ⅰ区在留沟期采用留沟内排时,产生的剥离物运输距离增大,卡车运输费用增高。先压帮后留沟相对于全压帮运距增量△L 可由先压帮后留沟内排方式的双翼内排运距减去全压帮的双翼内排运距计算得到。全压帮内排方式为双翼内排,其运距的数学公式与先压帮后留沟内排方式压帮期的双翼内排公式相同。

式中:F0为I 区增加的运距费用,元;V0为I 区剥离物体积,m3;△L 为运距增量,m;J 为单位运输成本,元/(km·m3)。
2.2 Ⅱ区增加的运距费用
Ⅰ区进行了部分留沟内排,在开采Ⅱ区时,部分剥离量仍不能进行双翼运输,从而导致Ⅱ区运费增加。Ⅰ区的压帮位置进行二次剥离开采,导致这一位置端帮角变缓,Ⅱ区运距相对于Ⅰ区发生改变。重复剥离示意图如图3。

图3 重复剥离示意图
分别计算出Ⅱ区在压帮期和留沟期的内排运距,由此可以得出Ⅱ区先压帮后留沟相对于全压帮的运距增量△L1。则Ⅱ区增加的运距费用为:


式中:F1为II 区增加的运距费用,元;V 为II 区部分剥离体积;△L1为II 区运距增量,m;θ 为端帮(松方)帮坡角,(°)。
2.3 Ⅱ区减少的重复剥离费用
对相邻采区公共端帮位置进行压帮内排,当下一采区开采时,为了回收相邻采区公共边帮处压的三角煤,必然需要进行重复剥离[12]。
先压帮后留沟内排方式压帮期增加的二次剥离费用与压帮的程度有关。全压帮时的重复剥离体积与压帮期的重复剥离体积做差即可求出先压帮后留沟压帮期对于全压帮减少的重复剥离体积V′。那么,减少的重复剥离费F2为:

式中:F2为I 区减少的重复剥离费用,元;V′为II 区重复剥离体积;J′为单位重复剥离费用,元/m3。
2.4 Ⅱ区减少的重复剥离运输费用
Ⅱ区单翼内排运距即为减少的重复剥离量V′的运距L3。所以,先压帮后留沟相对于全压帮减少的重复剥离运距费用F3为:

式中:F3为II 区减少的重复剥离运距费用,元;L3为减少的重复剥离运距,m。
2.5 最佳压帮内排转留沟工程位置确定
运用费用补偿法,即先压帮后留沟相对于全压帮在Ⅰ区和Ⅱ区增加的运输费用是否能通过Ⅱ区减少的二次剥离费用和二次剥离运输费用得以补偿。相邻采区的采剥工程推进往往存在时间差异。考虑现金的时间效应,二次剥离需滞后内排压帮n 年,且假设每年的内排剥离物都在相同的年以后进行二次剥离。则费用补偿值△F 为:

式中:△F 为费用补偿;p 为存款利率,%。
当△F<0 时,表示此压帮位置所减少的重复剥离费用和重复剥离运输费用的折现不能补偿两相邻采区共增加的运距费用。
当△F=0 时,表示此压帮位置所减少的重复剥离费用和重复剥离运输费用的折现恰好能补偿两相邻采区共增加的运距费用。
当△F>0 时,表示此压帮位置所减少的重复剥离费用和重复剥离运输费用的折现能充足的补偿两相邻采区共增加的运距费用。
因变量△F 是以压帮位置X 为自变量的一元二次函数,利用其性质建立函数图像。
因此,当△F>0 时的X 为最优压帮位置。影响△F 的因素很多,需要根据各露天矿的开采参数确定该矿合理的压帮位置。
3 实例分析
平庄煤业集团有限公司白音华一号露天煤矿采用分区开采,首采区和二采区为相邻采区。通过查看设计及咨询矿山技术人员综合得出计算所需参数,白音华一号矿各项开采参数见表1。

表1 白音华一号矿各项开采参数
将上述开采参数代入式(1)~式(8),计算可知:留沟长度在455.5 m 时,由双翼内排转为单翼内排。△F 的极值点在区间[0,4 000]内,且在有效区间内△F 为凸函数,因此存在最大值点。△F 与压帮长度变化曲线如图4,当压帮长度X=1 764 m 时,△F=0,此时减少的重复剥离费用和重复剥离运输费用的折现恰好能补偿两相邻采区共增加的运距费用。当压帮长度X=465 m 时,为最优压帮位置,此时△F=85万元。

图4 △F 与压帮长度变化曲线
4 结论
1)结合压帮与留沟内排的特点,提出了先压帮后留沟的内排方式,可以合理释放内排空间,减少运输费用和重复剥离费用,进而提高矿山生产的经济效益。
2)将先压帮后留沟内排方式分为压帮期和留沟期,建立了2 个时期运距的数学模型,确定了双翼内排转换为单翼内排时的条件为Hcotβ,为运输方式的转变提供理论依据。运用费用补偿法进行公式推导,建立一元二次函数,分析计算得出最优压帮长度。
3)结合白音华一号露天煤矿开采参数,确定留沟长度为455.5 m 时,双翼内排转变为单翼内排,确定最优压帮位置为X=465 m。
