曲率半径对凹边坡稳定性的影响

2021-01-05张晓敏黄皓轩

露天采矿技术 2020年6期

张晓敏，刘干，黄皓轩

（中煤科工集团沈阳设计研究院有限公司，辽宁沈阳 110015）

在露天煤矿的开采过程中，随着剥离上覆岩层，揭露埋藏的矿体，从而形成了边坡，在不断推进的过程中，边坡面与水平面的交线不断的变化，边坡面和水平面的交线呈直线分布的叫直边坡，如果交线呈曲线，曲率中心在采场的内侧叫凹边坡，曲率中心在采场的外侧叫凸边坡。在露天矿边坡工程中，在工作帮和端帮的交结处常会形成凹边坡。

在国外，ZHANG X[1]对凹边坡的三维稳定性进行了研究，认为稳定性与曲率有关。D W Rassam 和D J Williams[2]研究了矿上废石堆的极限稳定角，认为凹边坡的最大，平坡次之，凸边坡最小，其中凹边坡比平边坡大2°，凸边坡比平边坡小0.5°；朱乃龙和张世雄[3-4]研究了深凹边坡的稳定角，确定了稳定角的理论公式；李列列[5]和田钧[6]分别以瑞典法和bishop 法为基础，研究了边坡的旋转半径和土条侧向土压力的影响，分析了三维凹边坡的稳定性。

1 凹边坡力学分析

取一均质凹边坡进行力学分析，坡面形态为指向采场内侧的圆弧。R 为边坡的平面曲率半径，m；r为滑体内某一分条的平面曲率半径，m；H 为坡高，m；取圆弧角为dθ 的一段边坡作为研究坡体，g、s 分别为描述坡面和和滑面的函数；Ea为环向侧压力，kPa，方向与滑体下滑的方向相反。

由莫尔-库伦强度准则有：

式中：τ 为剪应力；σ 为正应力；Fs为安全系数；c为滑体黏聚力；φ 为滑体内摩擦角。

根据滑体的平衡条件，引入莫尔-库伦强度准则，设滑体面上的水平方向受力为E，切向受力为T，则：:

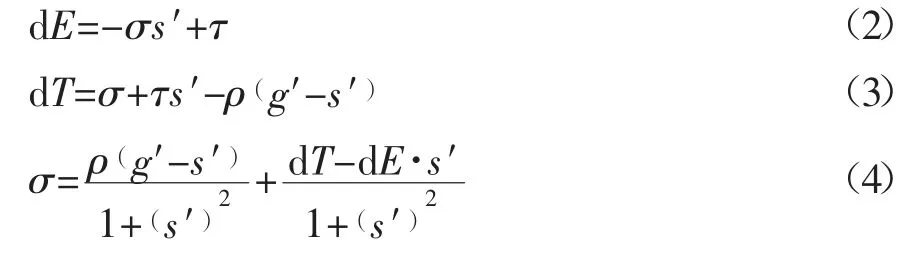
式中：s′、g′分别为s、g 的一阶导数；ρ 为密度。

从式（3）可以看出滑面正应力一部分是由滑体的体积力提供，另一部分是由土体条间作用力提供，卢坤林等经过大量的研究认为体积力为滑面正应力的贡献高达80 %，土体条间作用力只占20 %[7]，则可以认为滑面正应力σ 的分布情况即为滑体体积力的分布

根据静力平衡，可以建立3 个平衡方程：

式中：Ka 为朗肯主动土压力系数；a、b 分别为滑体出口与入口的坐标值。

由于滑面正应力的分布函数与半径有关，但其分布规律比较复杂，这里不做讨论。当c、φ、ρg 这些岩体参数不变，边坡高度H 不变时，可以知道Fs是1 个与半径r 有关的函数，半径越大边坡的稳定性越低，曲率半径越小的边坡稳定性越高。

2 数值模拟

2.1 数值模拟方法

数值模拟方法是确定边坡岩体某一区域内全部质点的应力和位移的分布情况[8]，分析边坡岩体变形破坏形式、范围和边坡稳定性的应力分析方法。采用数值分析方法，能够对具有复杂地形地貌、地质条件的边坡进行计算，不受边坡几何形状、边界条件以及材料的不均匀性限制，能够模拟边坡的渐进破坏过程，并提供应力、应变和位移等力与变形的全部信息，这些计算往往具有独特的结构、复杂的本构关系、载荷多样、计算量大的特点。边坡稳定性分析常用的数值分析方法有有限单元法[9]、边界元法[10]、离散元法[11]、不连续变形分析法[12]、拉格朗日法[13]。

数值模拟采用有限元强度折减法（SRM）[14]。为了衡量边坡的稳定性，使用强度折减法（SRM）进行计算，强度折减法在求解安全系数时，不需要假定潜在滑动面的形状和位置，也无需进行条分，而是由计算程序自动求出滑动面，强度折减法将衡量边坡稳定性的指标--安全系数Fos作为折减系数，将黏聚力c 和内摩擦角φ 进行折减，循环折减岩体强度直到边坡刚好达到临界失稳状态，以此获得边坡的稳定系数；通过分析模拟得到的位移云图、剪应变增量图和速度矢量场，获取边坡的滑移模式及力学机制。数值模拟使用大型数值模拟分析软件FLAC3D进行分析计算，该软件采用了显式拉格朗日算法和混合-离散分区技术，通过调整三维网格中的多面体单元来拟合实际的结构，单元材料可采用线性或非线性本构模型，当在外力作用下，网格能够相应发生变形和移动，非常适合于土质岩石和其他材料的三维结构受力特性模拟和塑性流动分析; 在计算分析中采用Mohr-Coulomb 准则，同时考虑剪切破坏和拉伸破坏，能真实地模拟边坡体的应力-应变关系[15]。

2.2 凹边坡数值模拟分析

为研究凹边坡曲率半径对边坡稳定性的影响，首先需要建立不同曲率半径的边坡，分别建立最下面的台阶半径为100、200、300、400、500 m 的5 个模型，由于要考虑模型的边界效应，所以模型采用不同的尺寸，模型尺寸见表1。模型的边坡高度H 为100 m，边坡角24°，坡面角34°。边坡采用均值模型，模型的岩体物理力学参数为：①密度:1.39 t/ m3；②黏聚力:25 MPa；③内摩擦角:13°；④弹性模量:680 MPa;⑤泊松比:0.27。

表1 模型尺寸

通过大型数值模拟软件FLAC3D对不同曲率半径的凹边坡进行强度折减计算，得到的边坡曲率半径与安全系数的关系如图2，不同曲率半径凹边坡边坡的位移云图如图3，不同曲率半径凹边坡剪切增量图如图4。

图4 不同曲率半径凹边坡剪切增量图

由图2 可知，凹边坡的曲率半径逐渐增大的过程中，边坡稳定系数逐渐减小，呈指数型下降趋势；这是由于相对于直线边坡，内凹边坡两侧环向侧压力合力不为0，合力作用方向与抗滑力方向一致，增加了边坡抗滑力；而当曲率半径大于400 时，安全系数的变化趋于稳定。由曲率半径对边坡稳定性的影响可知，曲率越大，边坡的安全系数越大，在工程实践中，工作帮与端帮的交接处会形成凹边坡，而提高凹边坡的曲率便可以提高边坡的稳定性，当曲率由1/500 提高到1/100，边坡的稳定性可以提高22 %，对边坡的安全生产有重要意义。

通过分析位移云图和剪应变增量图可知，位移呈现均衡分布，最大位移均出现在中间的台阶上，这是由于中间的台阶受到周围岩体的挤压作用，导致中间的台阶产生了较大的位移。剪切带在不同曲率半径下都已经贯通，并且在坡脚处的剪切应变最大，由剪切带的形式可以知道凹边坡的滑坡模式为圆弧滑动，并且在坡脚出容易出现失稳。