基于Rhino-Python的多圈高簇绒地毯三维仿真
2021-01-05代振兴陈广锋
代振兴,陈广锋,陈 革
(东华大学 机械工程学院,上海 201620)
织物外观模拟对于织物的设计生产意义重大,近年来已成为计算机图形学领域的研究热点。簇绒地毯在生活中可用于悬挂、垫坐或地面覆盖物等生活装饰用品,应用广阔,占据了地毯行业的主要市场份额[1]。但多圈高簇绒地毯绒圈空间结构复杂,高度不一,而且考虑到地毯美观方面的要求,其花型组合方式多变,大大增加了多圈高簇绒地毯外观仿真的难度。
国内有关地毯外观仿真的研究主要集中在地毯辅助设计工具的开发上,如浙大经纬CAD、蓝艺地毯集团的地毯CAD、China Dream等[2]。上述工具只能平面地模拟地毯花型设计图案,不具备簇绒地毯的外观结构模拟功能。另外,国内已对簇绒地毯外观模拟开展了一系列研究,但一定程度上忽略了簇绒地毯空间结构上的细节问题,仿真效果较差;国外学者对织物仿真方面的研究主要集中在多股加捻纱线模型构建以及服装面料真实感模拟等方面,如Zhao等提供了一种自适应构建多股纤维加捻及带有毛羽效果的纱线模型的方法;Cirio等在建立编织物三维模型时将经纬纱抽象为弹性杆模型来处理接触摩擦,但由于编织物与簇绒织物结构上的差异,该方法并不适合簇绒类织物的仿真[3-4]。国外有关簇绒地毯外观整体三维仿真方面的研究少见发布。
基于上述问题,针对簇绒地毯绒圈位置分布不规律、结构复杂等特点,本文通过设计算法基本实现了簇绒地毯的外观仿真。其中利用B样条曲线拟合原理建立了绒圈几何模型并真实地模拟了绒圈空间位置的偏转变形,增强了簇绒地毯外观仿真的真实感。
1 簇绒地毯三维仿真原理
1.1 簇绒地毯外观分析
簇绒地毯是通过簇绒针的往复机械运动将纱线穿过底布从而形成具有绒头的特殊织物;同时在簇绒过程中,通过改变喂纱量的大小来生成不同高度的绒圈,最终形成表面具有浮雕效果的多圈高簇绒地毯[5]。簇绒地毯基本结构如图1所示。
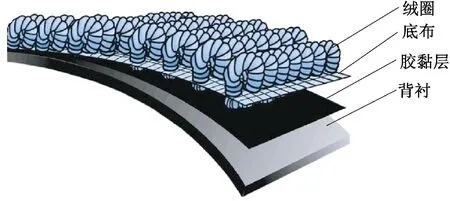
图1 簇绒地毯基本结构示意图Fig.1 Schematic diagram of basic structure of tufted carpet
可以看出,簇绒地毯的绒圈栽植和依附在地毯底布之上,并非整齐规则排列,而是经过栽绒定型、后整理等工艺阶段后受到相邻绒圈的挤压发生偏转变形[6]。并且绒圈空间结构上的受力变形极其复杂,具有一定的随机性。进一步发现,绒圈的变形主要有2种:绒圈自身在成圈过程中受到纱线张力的影响所产生的形变;绒圈整体受到其他绒圈的挤压后在原有针脚位置基础上发生了随机偏转。考虑到绒圈受力情况复杂,而且柔性纱线织物的受力研究起来比较困难,本文主要针对第2种偏转变形对簇绒地毯外观进行仿真模拟。
另外,簇绒地毯实际生产时绒圈是由多股单纱加捻后送入簇绒地毯织机织造而成的,为提高仿真效率,本文将绒圈看作由单股无加捻纱线织造而成。同时簇绒地毯结构只考虑底布的模拟,而胶黏层及背衬起到保护和固定绒圈的作用,文中簇绒地毯的外观仿真不再考虑二者的模拟。目前簇绒地毯底布多数为聚丙烯编织底布和非织造布底布,文中将底布简化为具有一定厚度的长方体模型,模拟时先生成底布,然后在底布上完成簇绒过程。
1.2 簇绒地毯三维仿真过程
考虑到簇绒地毯空间结构的复杂性,本文利用Rhino软件所支持的PythonScript模块通过程序算法实现了簇绒地毯整体外观的三维仿真。Rhino是一款适用于建立高精度的复杂三维非均匀有理B样条(NURBUS)模型的建模软件,结合PythonScript能够实现通过算法生成几何模型,并且可以自动执行大量重复的计算任务,提高了仿真效率。图2示出基于Rhino-Python的簇绒地毯三维仿真流程图。
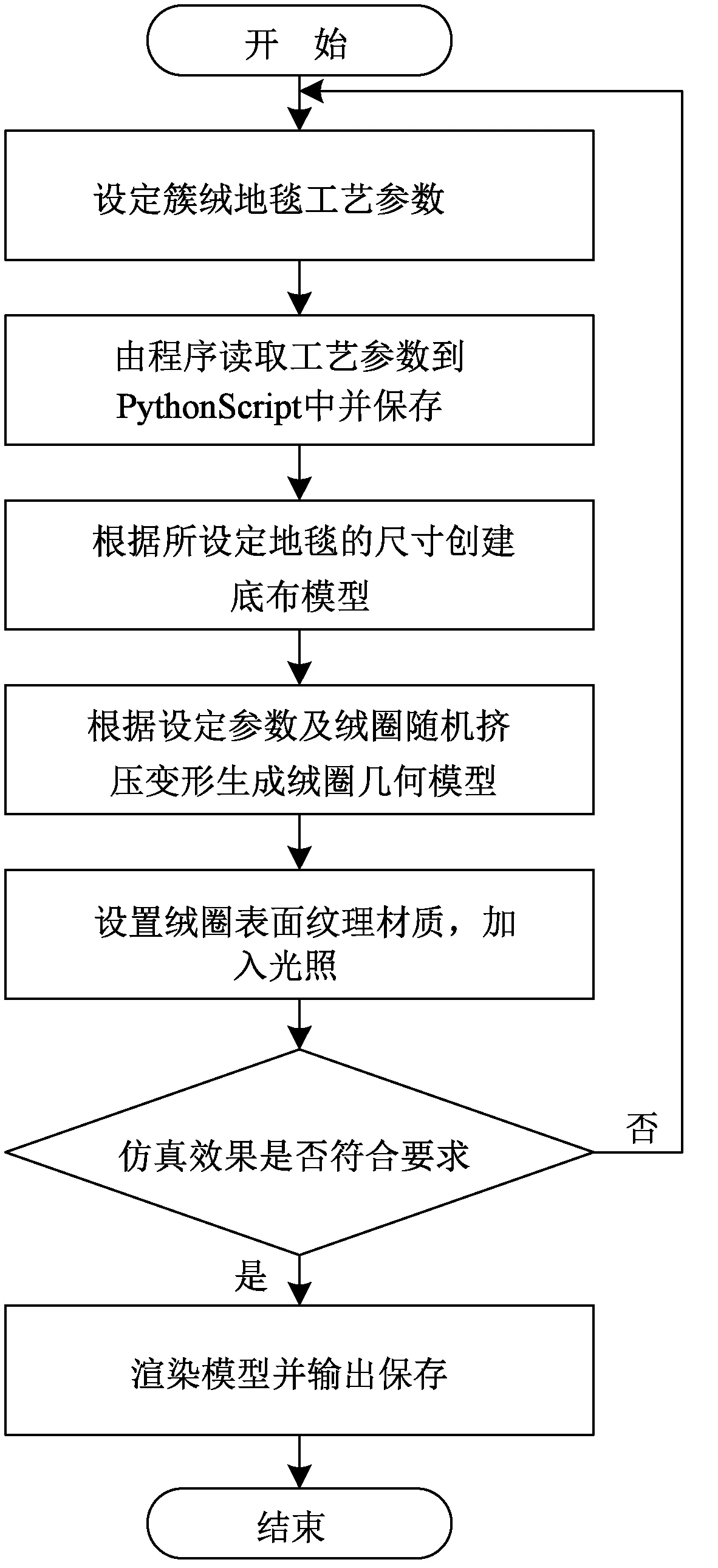
图2 簇绒地毯三维仿真流程图Fig.2 3-D simulation flow chart of tufted carpet
文中PythonScript开发环境下编写的簇绒地毯三维模拟程序采用模块化设计,主要包括地毯工艺参数读取、模型绘制、纹理添加等部分。其中,模型绘制程序对地毯绒圈受到挤压后所产生空间位置角度上的随机变化进行了描述,反映出地毯织造完成后绒圈分布的不规则性。绒圈表面纹理及光照的添加使地毯外观模拟获得更加真实的效果。本文最终初步实现了簇绒地毯的整体外观仿真,提供了一种可行的簇绒类织物三维仿真方案。
2 绒圈几何模型建立
对簇绒地毯的外观进行仿真,首先需要准确地建立绒圈的几何模型。单个绒圈几何模型的建立包括绒圈中心线的拟合以及绒圈截面形状的确定,本文均采用B样条曲线对二者进行拟合。文献[7]中提出将服装面料离散化成若干曲面后,在每个曲面上局部进行模拟计算[7]。同样地,本文将绒圈中心线及截面形状曲线离散分割成多段B样条曲线,分别局部计算各段样条曲线控制点值后再根据控制点坐标拟合出完整的绒圈中心线和截面形状。
2.1 绒圈中心线的B样条拟合
B样条曲线是一种分段多项式曲线,能够通过改变控制点坐标来改变曲线形状,而且计算速度快,效率高,常用于各类织物的三维仿真[8]。B样条曲线有均匀B样条曲线、准均匀B样条曲线和非均匀有理B样条曲线(NURBS)几种。理论上,NURBS可以表示任何曲线曲面,其他2种B样条都是其特殊形式。目前,通用的B样条曲线数学表达式为:
(1)
式中:P(t)代表B样条曲线;Pi代表控制点;Ni,k(t)为均匀B样条基函数;k用于控制曲线连续性的阶次;n等于控制点数目减1[9]。
工程界常用二次和三次B样条曲线(曲面),本文将绒圈中心线看成是由多段二次B样条曲线段衔接而成,来准确地描述绒圈中心线的屈曲形态。根据式(1)经过变换,可以得到由P0、P1、P2这3点定义的二次B样条曲线P(t)的表达式为:
(2)
再进一步,二次B样条曲线各段数学表达式均可写为关于t的抛物线式:
(3)

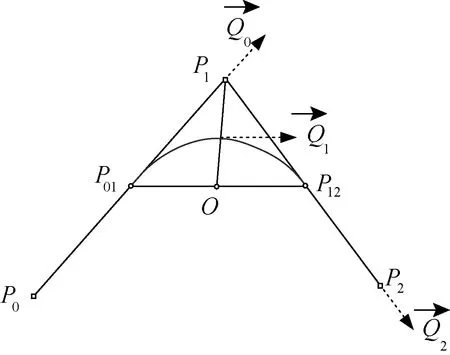
图3 二次B样条曲线拟合原理Fig.3 Principle of quadratic B-spline curve fitting
二次B样条曲线总是与特征多边形相切,根据二次B样条曲线端点位置向量以及端点切向量的性质[10],可以得到如下方程组:
(4)
利用高斯消元法结合MatLab求解方程组(4),可以求出控制点P0、P1和P2;然后将控制点代入式(2) 中求得表示绒圈中心线的二次B样条曲线;最后,利用坐标变换,结合绒圈中心线控制点值及切向量方程拟合出绒圈中心线。
本文将簇绒地毯绒圈中心线看成由多段二次B样条曲线拼接而成,利用上述方法分段进行求解,然后拟合出绒圈中心线。图4示出绒圈中心线的二次B样条曲线拟合,将绒圈中心线分割成5段二次B样条曲线(L1~L5),计算11个控制点值(P0~P10)来完成整个中心线的拟合。需要注意的是,每相邻2段B样条曲线衔接处会共用1个控制点(P2、P4、P6、P8),在计算过程中共用的控制点方程将作为隐含的条件辅助求解。
完成绒圈中心线的二次B样条曲线分割拟合设计后,按照上述求解方法计算出各控制点值,如表1 所示。但多圈高簇绒地毯各绒圈高度不同导致各个绒圈中心线控制点坐标也不相同,因此表1列出的是圈高为9 mm时未经扭转变形下的中心线控制点坐标,其他高度下控制点值计算方法相同。

图4 绒圈中心线的二次B样条拟合Fig.4 Quadratic B-spline fitting of center-line of the loop

表1 圈高为9 mm时绒圈中心线控制点坐标Tab.1 Coordinates of center-line control point of loop at loop height of 9 mm mm
将控制点值导入Rhino中,使用绘制控制点曲线命令便可以得到拟合出的二次B样条绒圈中心线,如图5所示。至此,完成了绒圈中心线的二次B样条拟合,后续整块地毯大量绒圈中心线的绘制遵循相同的拟合原理和求解方法,而且通过算法实现。

图5 Rhino中绒圈中心线绘制Fig.5 Establishing center line model of loop in Rhino
2.2 绒圈截面的近似表示
实际绒圈是由多股纱线经过加捻后形成的,其截面形状沿中心线方向并非处处相同,整体看来,地毯绒圈属于变截面实体[11]。本文为提高计算效率,将绒圈适当简化为等截面实体,且截面形状为圆形截面。将绒圈截面看作由4段90°圆弧连接而成,每段圆弧由3个控制点完成二次B样条曲线拟合,整个圆形截面曲线共由8个控制点拟合。
按照同样的计算方法,将求得的8个控制点坐标导入Rhino中,通过添加控制点曲线绘制出绒圈截面,如图6所示。
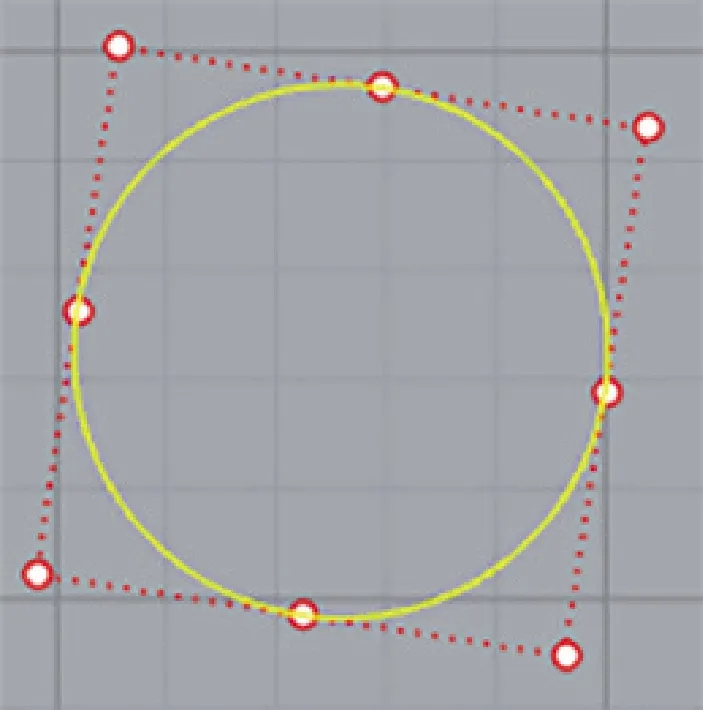
图6 Rhino中绒圈圆形截面表示Fig.6 Loop′s cross section in Rhino
完成绒圈中心线和截面形状的拟合后,在Rhino中通过绘制实体命令的调用,将绒圈截面沿中心线进行扫掠后得到绒圈的几何模型,图7示出2种不同圈高的绒圈几何模型。

图7 圈高为8 mm(左)和10 mm(右)的绒圈几何模型Fig.7 Geometric model with loop′height of 8 mm(left) and 10 mm(right)
通过分析利用B样条曲线构建绒圈几何模型的原理,同时研究如何求解出用于B样条曲线的控制点值,然后结合Rhino环境初步建立了单个绒圈实体模型,为整块地毯的仿真模拟作以铺垫。
3 簇绒地毯整体外观仿真
簇绒地毯在织造过程中经过簇绒、定型、覆胶及平整等工艺处理后,导致绒圈之间由于相互挤压发生了偏转变形[12],由前文簇绒地毯的外观展示也可以看出该特点。如何准确地模拟绒圈位置的偏转变形成为簇绒地毯外观仿真需要解决的关键问题。
3.1 绒圈偏转变形模拟
绒圈整体空间位置的偏转变形是受到绒圈挤压后随机产生的,主要表现为绒圈以毯面法线方向为旋转轴偏转了一定的角度[13],图8示出绒圈产生空间位置偏转变形示意图,未偏转绒圈与偏转绒圈之间形成了偏转角β。经过观察地毯实物测量统计得出,绒圈受到挤压后在空间位置上的偏转角度不超过±45°。因此,簇绒地毯外观仿真的关键在于准确地表征偏转角(允许范围为±45°)。

图8 绒圈空间位置偏转变形示意Fig.8 Deflecting and deforming about spatial position of loop
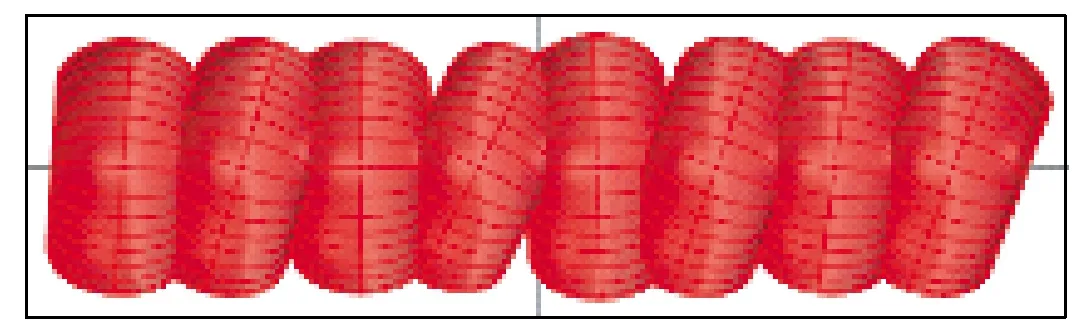
图9 绒圈偏转变形模拟效果Fig.9 Effect of loops deflecting simulation
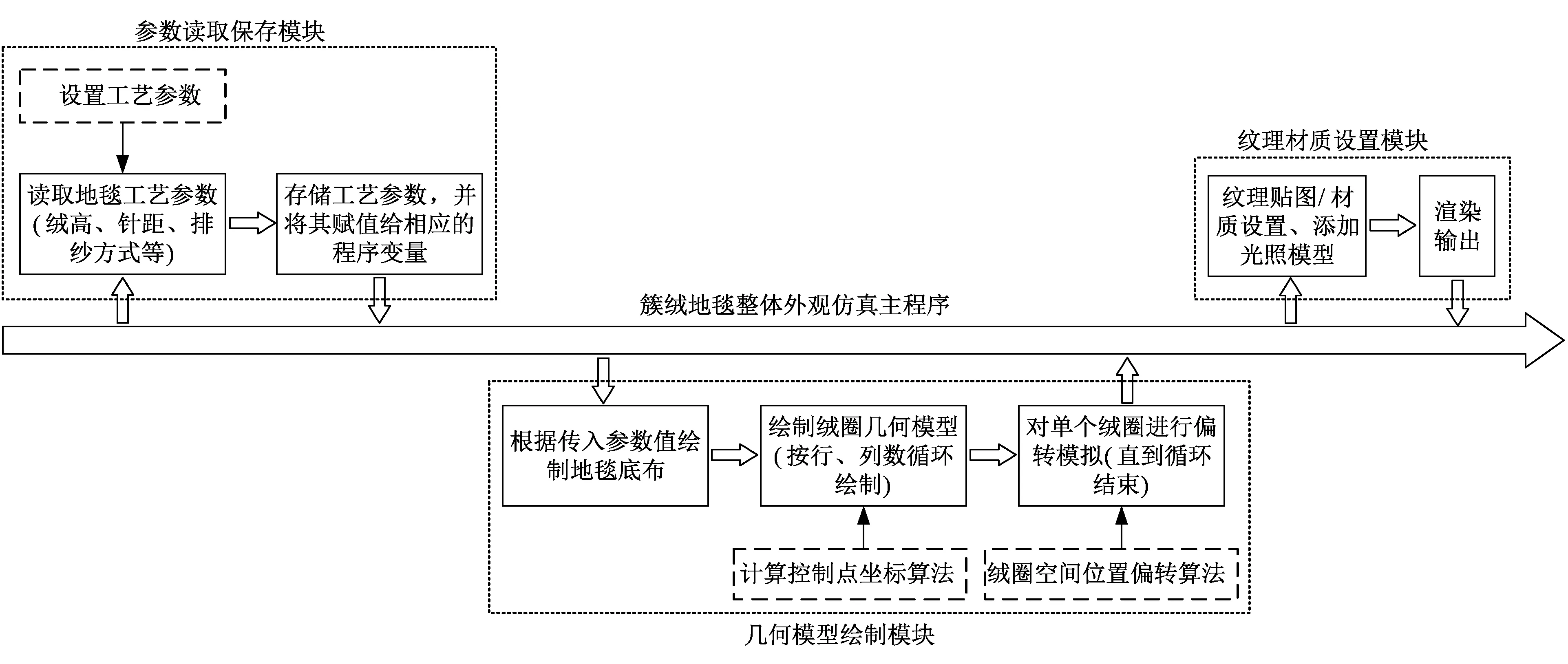
图10 簇绒地毯外观整体仿真程序框架Fig.10 Tufted carpet appearance overall simulation program framework
由于绒圈受力情况复杂,各个绒圈受力均不相同导致其发生偏转变形并且呈现随机性,因此本文对偏转角β的随机模拟借助Python中随机数生成函数random()来完成。通过设计程序算法在每次完成绒圈几何模型绘制后,调用以随机数为主要参数的位置偏转函数对绒圈空间位置进行偏转,偏转角度在允许范围(±45°)的计算公式为:
β=(random(t)-0.5)×90
(5)
式中,random(t)为随机数生成函数,在Python中该函数可以生成(0,1)内的任意实数,为保证偏转角在±45°范围内,添加权重为90。
那么对应到Python中偏转角的计算和偏转实体相应的程序代码为:
xform=rs.XformRotation2((random.random()-0.5)×90, [0,0,1],center_point)
其中,xform在Python中表示绒圈偏转后的实体对象。XformRotation2()为偏转实体函数,该函数所需的3个参数分别为偏转角度,偏转中心轴向量以及偏转轴起始点。
例如,在绒圈高度分别为3,4,5,…,9,10 mm时,根据程序运行结果,各绒圈高度下对应的绒圈偏转角度为-5.181°,-24.466°,3.501°,…,-12.098°,-28.921°,每个绒圈所偏转的角度均保证在允许范围内。当然,每次程序运行后所生成偏转角的值都是不一样的,确保绒圈偏转的随机性。实际绒圈随机偏转的模拟效果(从左至右绒圈高度递增)如图9所示,完成了对绒圈空间位置偏转的随机模拟。
3.2 簇绒地毯的仿真实现
在完成单个绒圈几何模型绘制及其随机偏转模拟的研究后,本文基于Rhino中的PythonScript开发环境设计了簇绒地毯整体外观仿真算法,实现了对簇绒地毯外观的整体仿真。程序主要由3大模块组成,包括参数读取保存模块、几何模型绘制模块以及纹理材质设置模块,程序整体框架组成如图10所示。
其中,对于簇绒地毯工艺参数的设置包括绒圈高度、绒圈数量、地毯尺寸规模以及多种地毯花型、材质的设置,以获得不同风格外观的地毯。绘制绒圈几何模型时按所设置的绒圈行、列数共2层循环完成所有绒圈的绘制,可以满足任意大小的地毯尺寸要求。纹理贴图及材质的设置通过将纱线的材料纹理映射到绒圈表面来增强仿真效果。
区别于前人有关簇绒地毯仿真模拟的研究,文中将簇绒地毯外观仿真程序按照功能划分为多个模块,通过模块间的相互协作实现簇绒地毯的外观仿真。例如运行参数读取子程序获得当前仿真地毯工艺参数,包括纱线信息、排纱规律以及花型数据,将其传递给几何模型绘制模块完成地毯整体仿真模型构建,提高了程序的易读性和可维护性,使得簇绒地毯的外观仿真实现起来更加便捷。
将仿真结果与地毯实物样品进行对比,如图11所示。通过运行程序可以发现,绒圈偏转变形的模拟达到了较为真实的效果,同时对比结果充分表明上述簇绒地毯三维仿真方案的可行性。

图11 簇绒地毯外观仿真效果与实物对比Fig.11 Comparison between tufted carpet appearance simulation and product. (a)Simulation; (b)Finished product

图12 不同花型簇绒地毯整体外观仿真效果Fig.12 Overall appearance simulation of tufted carpets with different patterns. (a) Pattern of "DHU"; (b) Pattern of wave; (c) Pattern of hound′s-tooth; (d) Pattern of Twill
另外,不同的花型设置可通过改变绒圈高度及绒圈排列方式任意组合获得,以下列举出了多种花型图案的多圈高簇绒地毯仿真结果,如图12所示。相比于传统的二维模拟,三维仿真技术使得地毯外观看起来更加真实。其中,图12(a)模拟的是带有字体花型图案的簇绒地毯,通过控制字体突出位置的绒圈高度高于其他位置的绒圈,使字体图案凸显出来,形成高低绒圈遮挡效果。实际簇绒地毯织造过程中是通过控制簇绒针排中的某根单针系统的传动比改变其喂纱量以及将多个针排模块并联组合后再进行织造,从而在相应字体位置形成高绒圈而其他位置仍保持同一高度。图12(b)~(d)中通过相同的方法模拟出高低绒圈组合出的不同花型的簇绒地毯。
另外,与之前国内有关学者开展的簇绒地毯外观仿真方面的研究相比,本文模拟了簇绒地毯绒圈在经历复杂的工艺过程(栽绒、定型、后整理等)后发生不规则形变的状态,设定绒圈高度相同的条件下,每个绒圈由于受到挤压产生变形导致其高度、大小、偏转角度及方向各不相同。如图12所示,达到的整体仿真效果相较于已有的研究更加真实。从图中还可以看出,文中提出的簇绒地毯外观仿真方法对结构复杂的簇绒地毯取得了较好的仿真效果。理论上,该方法适用于多种圈高组合的任意花型簇绒地毯外观三维仿真,但对于由多股单纱加捻后编织的簇绒地毯以及割绒地毯的仿真仍需进一步研究。
4 结 论
本文基于二次B样条曲线建模理论,利用Rhino软件中的PythonScript对簇绒地毯进行三维仿真,达到了更加真实的效果。在绒圈几何模型建立过程中,分析了利用B样条曲线控制点拟合绒圈中心线及截面轮廓的方法,完成了绒圈几何模型的绘制。考虑到实际绒圈之间因相互挤压作用会产生形变,对绒圈的随机偏转变形进行了模拟。最终,将控制点求解过程及绒圈空间位置偏转算法写入到簇绒地毯外观仿真算法程序中,实现了簇绒地毯整体外观的基本仿真,并且模拟出了多种花型图案、绒圈高度变化的簇绒地毯。通过比较模拟图与实际地毯样品,仿真结果具有一定的可靠性。
