自润滑关节轴承衬垫弹性参数的计算

汪久根，郭 昊，洪玉芳，陈芳华

(1. 浙江大学 机械工程学院，浙江 杭州 310027； 2. 浙江省机电产品质量检测所，浙江 杭州 310051)

衬垫关节轴承是一种球面滑动轴承，因为具有良好的承载能力、减摩抗磨能力，常用于汽车、矿山机械和航空领域[1-2]。衬垫关节轴承主要结构是一个带内球面的轴承外圈、粘贴在轴承外圈内球面的自润滑衬垫和一个带外球面的轴承内圈组成。目前衬垫关节轴承的衬垫普遍采用纤维编织复合材料[3]。纤维编织复合材料是摩擦因数较小的纤维与其他材料(例如碳纤维、玻璃纤维等)通过一定的方式编织而成，与轴承内圈外球面相接触的工作面以摩擦因数很低的聚四氟乙烯纤维(PTFE)为主，与轴承外圈内球面相接触的黏结面以高强度、易黏附的纤维(如Kevlar纤维等)为主[4]。

衬垫宏观上属于正交各向异性材料，目前主要通过细观力学方法，利用复合材料各组成部分预测其宏观弹性性能[5]。左中鹅等[6]基于平纹织物层合板内纱线的细观分布, 建立具有双凸结构的特征体积单元有限元模型，通过数值分析计算复合材料模量, 并根据复合材料内纤维与基体的失效准则预测单胞强度。刘召磊等[7]通过研究玻璃纤维和碳-50基体编织织物衬垫，在刚度平均的基础上结合几何模型，提出了斜纹织物衬垫弹性性能解析模型。王东宁等[8]建立了平纹织物三维细观几何模型，对弹丸冲击响应进行了模拟。陈纪刚等[9]用数值模拟和解析法对修正的衬垫特征体元模型进行了计算，并与实验数据进行比对验证。卢建军等[10]提出了PTFE/Kevlar斜纹编织衬垫不同磨损深度下的磨损模型，并与实验进行对比。上述研究中建立的衬垫特征体元几何模型与实际偏差较大，且弹性参数计算值与实验值相对误差较大。

本文结合自润滑关节轴承衬垫的压紧预处理过程，对衬垫的特征体元细观几何模型进行了修正。在此基础上，利用桥联矩阵[11]，提出了改进的编织衬垫弹性参数的预测模型，并与其实验结果进行比对，以验证本文提出模型的准确性。

1 编织方式

纤维编织衬垫材料的编织方式主要分成机织、编织、针织3类。机织的编织方式分为平纹、斜纹、缎纹等[11]。本文采用的平纹、一上二下右斜纹(以下简称为斜纹)、五枚二飞缎纹(以下简称为缎纹)3种编织结构如图1所示。

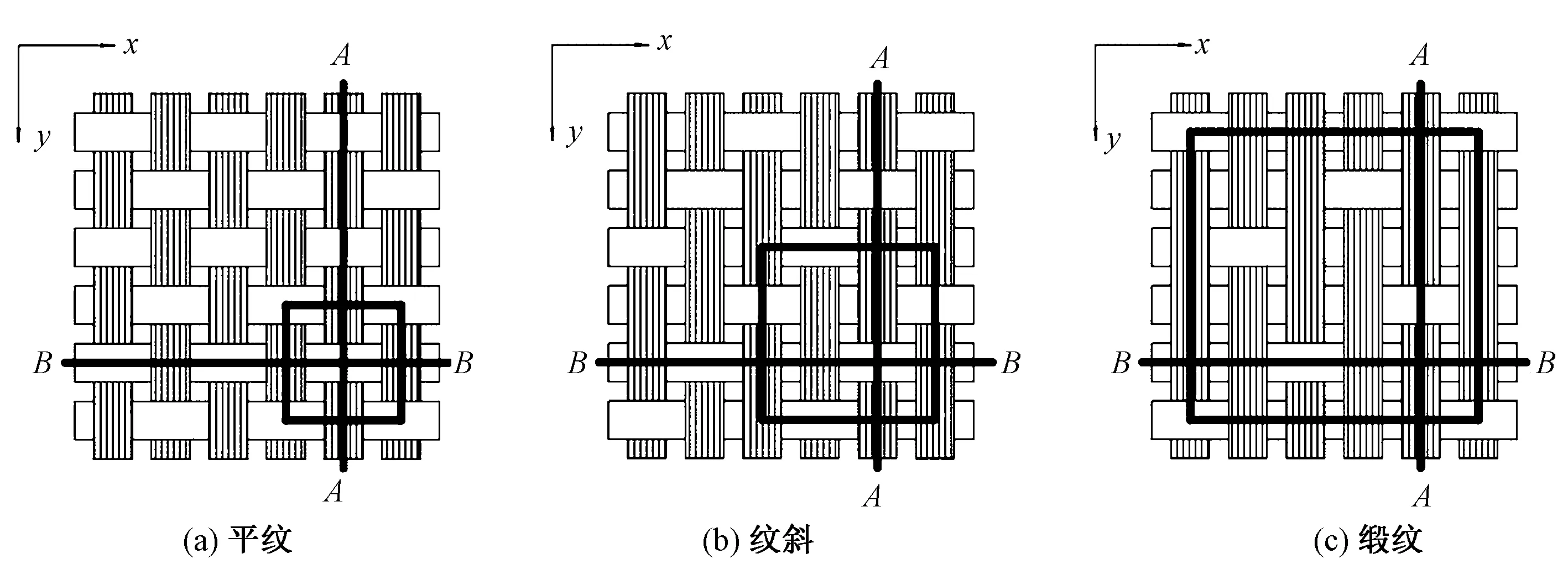
图1 平纹、斜纹、缎纹衬垫结构示意图Fig.1 Microcosmic structures of plain(a), twill (b) and satin (c) fabric liners

2 桥联矩阵

对于复合材料，通常的做法是取特征体元进行研究。特征体元有如下特征：

1)整个复合材料可以由特征体元的重复叠加得到。

2)复合材料的等效力学量相对特征体元而言是连续或者有定义的。

特征体元是具备前2条特征的最小体积单元，相当于各向同性材料中的一个几何点，各力学量必须相对特征体元取平均值。

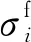
(1)

式中，Aij为桥联矩阵，在弹性范围内，正应力与剪应力不耦合。桥联矩阵具有如下形式[13]：

(2)

式中：aij为桥联矩阵元素。

本文主要用桥联矩阵计算自润滑关节轴承衬垫纤维束特征体元的横向弹性模量、面内剪切模量、横向剪切模量，从而进一步计算得到衬垫宏观等效弹性参数。

3 编织衬垫弹性参数理论分析模型

衬垫经向和纬向纤维束都假定为横观各向同性，对称轴为纤维束的轴线。近年来在对于衬垫的细观结构研究中，纤维束截面都依照Lee等[14]给出的透镜形状，如图2所示。

实际上在编织衬垫使用之前，为达到最终的高纤维体积分数，还需对衬垫进行压紧预处理，经过有限次的加载、保持、卸载的循环之后，纤维束截面形状和波形都发生了变化[15-18]。

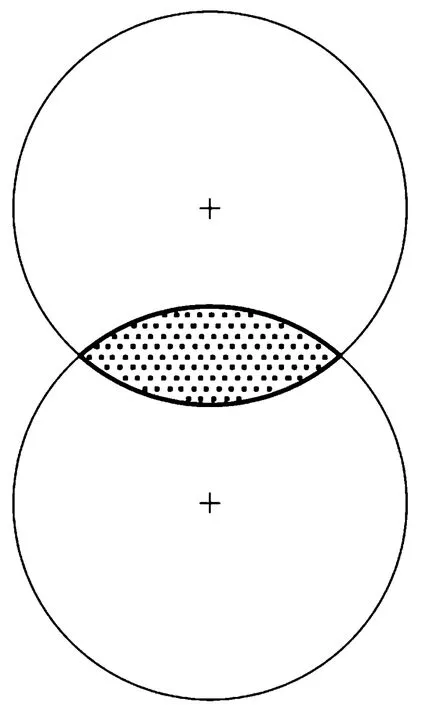
图2 透镜形纤维束截面示意图Fig.2 Lenticular cross-sectional shape of yarn

以平纹编织衬垫为例，压紧预处理前后的纤维束波形和截面形状如图3所示。图中：w0、d0、H0为压紧预处理前纤维束宽度、厚度、衬垫厚度；w、d、H为压紧预处理后纤维束宽度、厚度、衬垫厚度。纤维束截面形状由椭圆形变为趋近于由正弦曲线段和直线段围成，纤维束波形由正弦曲线变为趋近于由直线段和正弦曲线段组成。

为此，提出了修正的衬垫特征单元细观几何模型。纤维束截面形状如图4所示，上下轮廓线对称，由2曲线段和1直线段组成。为表示方便，取纤维束厚度方向为z轴，宽度方向为x轴，记纤维束厚度为d，纤维束宽度为w。

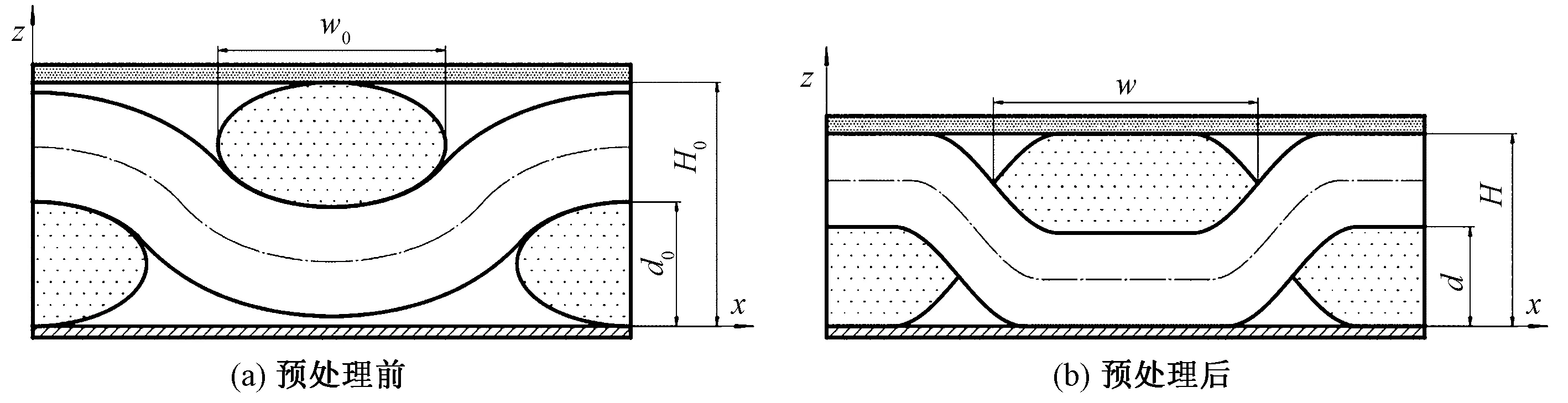
图3 平纹衬垫压紧预处理前后结构示意图Fig.3 Structure of plain fabric liner before(a) and after(b) compaction preform

图4 纤维束截面示意图Fig.4 Cross-sectional shape and size of yarn

纤维束截面轮廓线第1条曲线段方程如下：

(3)

纤维束截面积A为：

(4)

3.1 纤维束体积分数

平纹衬垫特征体元(RVE)沿A-A的截面如图5所示。下角标w、f、m分别表示经向纤维束参数、纬向纤维束参数、基体参数。

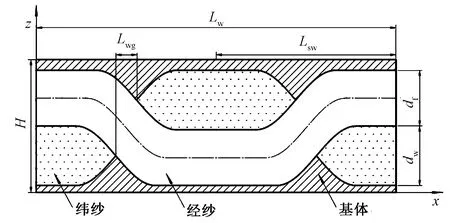
图5 平纹衬垫特征单元A-A截面示意图Fig.5 A-A cross section of RVE of plain fabric liner

dw、df分别为经向纤维束和纬向纤维束的厚度；H为特征体元厚度。

经向纤维束直线段长度

Lsw=wf+Lwg

(5)

式中：wf纬向纤维束宽度；Lwg是经向纤维束间隙。

纤维束弯曲部分长度

(6)

式中，z′为z的一阶导数。

经向纤维束的总长度

Law=nLsw+Lwg+Lcw,n=1,2,3

(7)

式中，n=1,2,3，分别对应平纹、斜纹、缎纹结构。

特征体元经向长度

Lw=kLsw,k=2,4,5

(8)

式中，k=2,4,5，分别对应平纹、斜纹、缎纹结构。

特征体元内经向纤维束体积

Vw=kALcw

(9)

特征体元的体积

V=LwLfH

(10)

式中，Lf为特征体元纬向长度，Lf=Lw。

特征体元中经向纤维束的体积分数φw为：

φw=Vw/V

(11)

Vf为纬向纤维束体积，特征体元中纬向纤维束的体积分数φf为：

φf=Vf/V

(12)

因此得到特征体元中基体的体积分数φm为：

φm=1-φw-φf

(13)

3.2 衬垫弹性常数

衬垫柔度矩阵计算流程如图6所示。

图6 衬垫柔度矩阵计算流程Fig.6 Flow chart of compliance matrices of liners

计算经向纤维束的5个独立弹性常数的公式如下式所示。其中：轴向弹性模量E11以及轴向泊松比ν12用Chamis模型[19]计算；横向弹性模量E22、面内剪切模量G12以及横向剪切模量G23用桥联模型[12]计算。

(14)

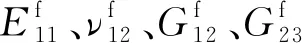
(15)

mi(i=1,2,3,4,5,6)[12]分别为：

(16)

文献[13]给出了桥联矩阵Aij的元素：

(17)

式中：α和β是桥联参数，取值范围在0～1之间[19]。对不同的纤维和基体组成的纤维束，可根据实验测得的横向模量和剪切模量来调节桥联参数取值。

另外，横向泊松比ν23可由下式求得：

(18)

经向纤维束在局部坐标系下的柔度矩阵Sij为

(19)

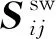
(20)

经向纤维束弯曲部分可以看成是有限个微小直线纤维束段组成，各纤维束段的局部坐标系(x1,x2,x3)与整体坐标系(x,y,z)下的柔度矩阵的转换矩阵Tc为[20]

(21)

经向纤维束弯曲部分整体与局部坐标系关系如图7所示。

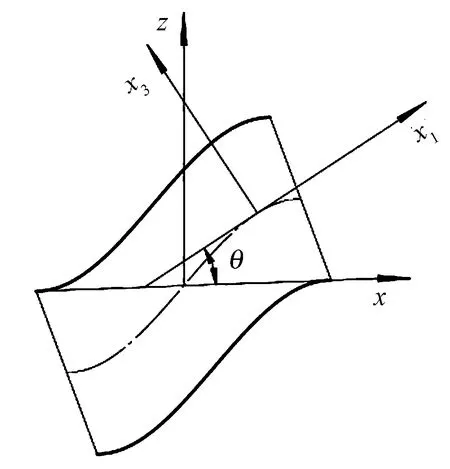
图7 纤维束弯曲部分示意图Fig.7 Curve part of fiber yarn

x轴与x1轴夹角θ为

(22)

由此得到经向纤维束弯曲部分在整体坐标系下的柔度矩阵：

(23)

经向纤维束直线部分和弯曲部分的长度分数λs、λc分别为：

(24)

λs=1-λc

(25)

经向纤维束整体坐标系柔度矩阵：

(26)

(27)

(28)

(29)

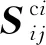
(30)

式中，φf为特征体元中纬向纤维束的体积分数。

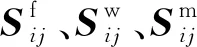
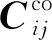
(31)

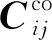
(32)

4 实验结果对比分析

利用上述几何模型和弹性参数计算模型，对文献[9]中斜纹衬垫和文献[21]中平纹、缎纹衬垫的宏观弹性参数进行计算。

文献[21]中平纹衬垫经向和纬向纤维束为PTFE纤维束，基体为酚醛树脂。在Zwick/Roell公司的BZ2.5/TS1S型电子织物强力机上，以 0.2 mm/min 恒定的加载速度对平纹和缎纹衬垫试样进行拉伸强度测试。CCD相机放置在样品的表面，以便在加载过程中对试样的应变进行图像记录，应变测量的精度为0.005%。用数字图像相关分析方法来处理得到的顺序图像，从而得到衬垫的拉伸应力应变图，以及平纹和缎纹衬垫的x方向和y方向弹性模量、沿x方向剪切模量。

文献[21]中平纹和缎纹衬垫的纤维束宽度0.100 mm，厚度0.190 mm，间隙 0.067 mm，纱线填充率0.700。材料参数如表1所示。

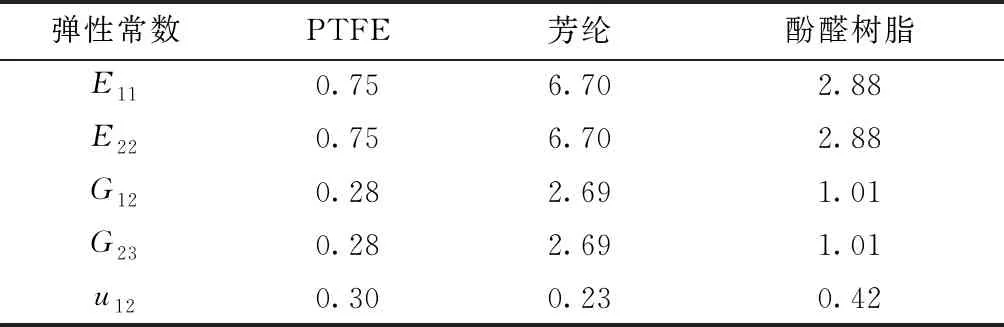
表1 平纹和缎纹衬垫材料弹性参数Tab.1 Elastic parameters of materials of plain and satin fabric liners GPa

将上述参数代入文中提出的模型计算，得到整体坐标系下平纹衬垫弹性参数。与实验值比较结果如表2所示。综合对比发现，经向和纬向纤维束计算中α和β分别取0.6、0.1时准确度最高，最大误差4.76%，最小误差0.51%，本模型计算该平纹织物衬垫的宏观弹性参数具有可行性。

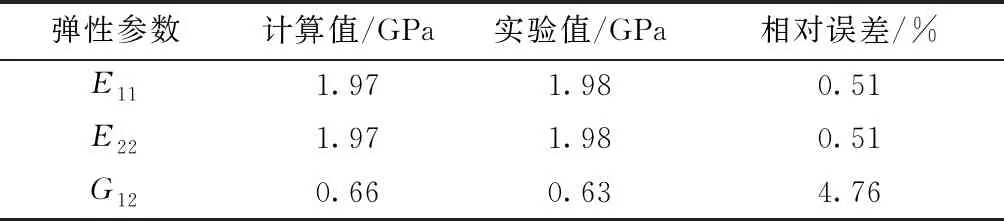
表2 平纹计算结果与实验比对Tab.2 Comparison between computational and experimental results of plain fabric liner

文献[9]中斜纹衬垫经向纤维束为 PTFE纤维束，纬向纤维束为芳纶纤维束，基体为酚醛树脂。取有效宽度为50 mm、有效长度为100 mm的斜纹衬垫，在Y511B型电子织物强力机上以 20 mm/min 测试拉伸强度。在自制的实验机上沿衬垫的布面方向进行压缩实验，记录压缩力与变形数据。依据实验数据获得斜纹衬垫x方向和y方向弹性模量。纤维束的几何参数和材料参数分别如表3、4所示。

表3 文献[9]中斜纹衬垫纤维束几何参数Tab.3 Geometric parameters of yarn of twill fabric liner

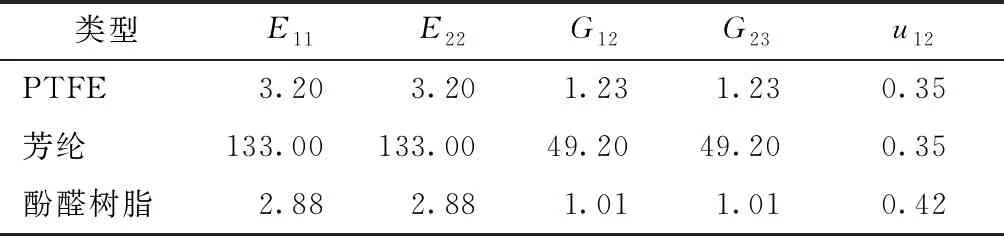
表4 文献[9]中斜纹衬垫材料弹性参数Tab.4 Elastic properties of materials of twill fabric liner GPa

将上述参数代入文中提出的模型计算，得到整体坐标系下斜纹衬垫弹性参数与实验值比较，结果如表5所示。综合对比发现，经向纤维束计算中α和β分别取0.2、0.6，纬向纤维束α和β分别取0.1、0.4时准确度最高，最大误差5.47%，最小误差2.58%，本模型计算该斜纹织物衬垫的宏观弹性参数具有可行性。

表5 斜纹计算结果与实验比对Tab.5 Comparison between computational and experimental results of twill fabric liner

文献[21]中缎纹衬垫经向纤维束为 PTFE和芳纶纤维束，纬向纤维束为芳纶纤维束，基体为酚醛树脂，纤维束的几何参数与平纹衬垫相同。

将上述参数代入文中提出的几何模型和弹性参数模型计算，得到整体坐标系下缎纹衬垫弹性参数，与实验值结果比较如表6所示。综合对比发现，经向纤维束计算中α和β分别取0.9、0.4，纬向纤维束α和β分别取0.4、0.9时，准确度最高，最大误差4.39%，最小误差小于0.01%，本模型对于计算该缎纹织物衬垫的宏观弹性参数具有可行性。

表6 5/2缎纹计算结果与实验比对Tab.6 Comparison between computational and experimental results of satin fabric liner

用于计算不同纤维束弹性常数的桥联参数，可通过对纤维束进行简单拉压剪切实验确定。

5 结 论

本文对编织衬垫几何模型进行了修正。利用桥联模型提出了适用于多种编织衬垫的弹性参数解析模型。

1)通过与实验进行比对，进行模型与计算方法的有效性验证。结果表明，本文提出的模型得到的计算结果与实验结果吻合性较好。

2)在运用本文提出模型计算编织衬垫弹性参数时，若纤维束中纤维和基体沿轴线方向弹性模量比值较大，所得结果较为准确。后续可对衬垫纤维束进行拉压剪切实验来确定桥联参数值。

3)通过此方法获得的结果，为衬垫轴承的磨损分析提供衬垫宏观弹性参数，可用于自润滑关节轴承进一步研究中。