基于介电谱的醋酸酯水刺非织造布含水率估算

吕汉明，王翔宇，刘凤坤

(1. 天津工业大学 纺织科学与工程学院，天津 300387； 2. 中国纺织信息中心，北京 100025)

在水刺非织造布的生产过程中，厂家通过烘燥来控制下机非织造布的含水率。目前常用的纤维材料水分测试方法有烘箱法和直流电阻测湿法，其中烘箱法测试结果准确、稳定，被GB/T 9995—1997《纺织材料含水率和回潮率的测定 烘箱干燥法》定为仲裁检验和纺织厂质量控制检验的基本方法。快速方便的直流电阻测湿法也被众多纤维材料收购部门和纺织厂质检部门广泛使用。烘箱法耗时耗能，不利于快速检测，直流电阻测湿法因纤维的直流电阻很大，极板易被极化而导致测量稳定性差，误差大，通用性差[1]。

电容传感器具有成本低、分辨率高和相对容易实现等优点，可以不破坏被测物表面对其进行含水率检测[2-3]。在工频50 Hz时，干燥纺织材料的介电常数约为2～5，而液态水的介电常数为20，吸附水分子的介电常数为80。纺织材料吸水后其含水率增大介电常数也随之增大。Peeters[4]搭建了测量羊毛干态质量和回潮率的实验装置，该装置也能测试吸湿性较差的纺织材料。文献[5-6]研究了机织物的介电常数，比较了不同组分的空气-纤维混合体的介电常数，研究了空气、水分、锦纶6长丝三相混合体的介电常数，并发现介电常数与织物体积分数呈二次曲线关系。Lü等[7]指出在电场频率为0.9～20 MHz时干燥醋酸纤维试样的体积分数与介电常数呈线性关系，醋酸纤维束的介电常数随着样品中水的体积分数增加而增加，随着频率的增加而减小。当电场频率大于100 kHz时，棉纤维的介电常数与回潮率呈线性关系，当电场频率远小于100 kHz 且棉纤维回潮率小于3%时，棉纤维的介电常数与回潮率近似线性关系[8]。

本文测量并分析醋酸酯水刺非织造布的介电谱，建立了非织造布体积分数与其介电常数的关系，水体积分数与其介电常数的关系以及含水率与试样单位质量介电常数变化率之间的关系，为用电容传感器检测水刺非织造布含水率提供了基础。

1 实验部分

1.1 实验材料和仪器

实验样品为：15片直径4 cm、面密度53 g/m2、 厚度0.8 mm的圆形醋酸酯水刺非织造布。

Novocontrol BDS50型介电谱仪(电场频率为1～1×106Hz)。 OHAUS先行者分析天平(量程为0～220 g，标尺分度为0.000 1 g)。Sartorius MA150型水分分析仪。

1.2 实验方法

1.2.1 特定含水率非织造布的制备

由于醋酸酯纤维在140～150 ℃条件下开始发生变形，在温度为176 ℃时醋酸酯纤维会发生黏结，因此在含水试样制备中所使用的烘燥温度为105 ℃。

烘燥过程中，水分分析仪会显示挥发水分质量和试样湿态质量的比值，本文称之为烘燥量。当试样被完全烘干时，烘燥量就是试样的含水率。

由于停止加热后试样中的水分还会继续挥发，为能比较准确地制备特定含水的试样，采用3段式烘燥法对试样进行烘燥。具体过程为：

1) 取1～5片醋酸酯水刺非织造布试样烘干并记录其干态质量，将干燥的非织造布浸入去离子水中至其不再有白色气泡时用镊子取出悬空，待相邻2次滴水时间间隔大于15 s时，对其进行第1次烘燥，烘燥量为40%。

2) 更换样品盘进行第2次烘燥，烘燥量为50%。

3) 更换样品盘进行第3次烘燥。先用式(1)计算预设含水率为a时非织造布的湿态质量，再用式(2)计算第3次的烘燥量A，第3次烘燥过程中，当水分分析仪显示烘燥量为A时停止烘燥，此时非织造布的含水率在a左右。

w=M(1+a+0.05)

(1)

A/100=(1-w/w1)-0.05

(2)

式中：w为具有特定含水率的试样湿态质量，g；w1为第2次烘燥后试样的湿态质量，g；M为试样的干态质量，g；a为预设含水率，%；式(1)中0.05为试验得出的修正值，主要用来弥补因试样余热造成水分挥发而形成的误差。

水刺非织造布的下机含水率一般控制在6.0%左右[9]，本文所制备试样的含水率为0%～15%，完全涵盖水刺非织造布的下机含水率范围。

1.2.2 样品电容的制备

用1.2.1制备的具有一定含水率的非织造布样品制备样品电容。用2个直径为40 mm的镀金铜电极片2和内径为32 mm、高为5 mm的聚四氟乙烯垫圈1组成1个空的电容器，称之为空电容器，如图1所示。聚四氟乙烯垫圈可以使上下2片电极定位对准且保持5 mm的间距，从而使样品3处于一个体积恒定(4.021 2 cm3)的空间[10]，在电极之间放入非织造布的电容器称之为样品电容。改变样品(醋酸酯纤维非织造布)的片数和含水率，研究其体积分数与水分体积分数对介电常数的影响。

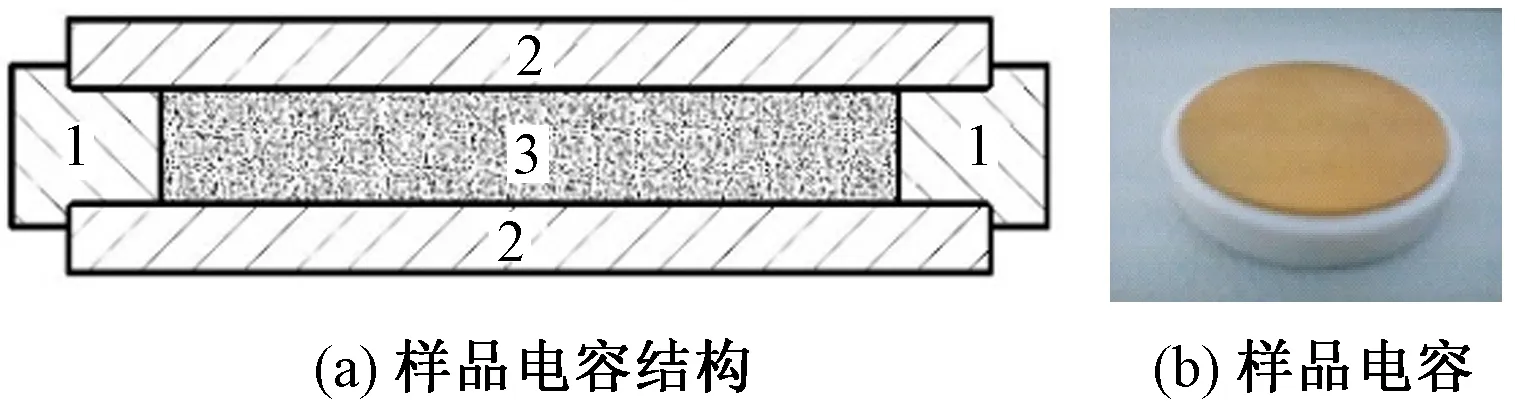
1—聚四氟乙烯垫圈； 2—镀金铜电极片； 3—样品。图1 样品电容的结构与电容器Fig.1 Sample capacitor structure and capacitor. (a)Sample capacitor structure; (b)Sample capacitance

1.2.3 性能测试

在介电谱仪操作软件中输入空电容器的参数和测试频率，为抵消分布杂散电容和边缘电容对实验结果的影响，应在操作软件中输入补偿值，使空样品电容介电常数实部接近1.0。

在空电容器中放入不同片数的干燥试样来研究非织造布体积分数对介电常数的影响。在空电容器中放入不同片数及含水的试样测试，结合非织造布的体积分数对介电常数的影响来分析水的体积分数对介电常数的影响。综合所有数据研究试样含水率与其单位质量介电常数变化率的关系。在测试过程中，试样的含水率会有少许的改变，因此在测试前和测试后对试样进行2次称量，以2次称量的平均值计算试样测试时的含水率h。

式中：M1为干燥试样的质量，g；m1为测试前试样的质量，g；m2为测试后试样的质量，g。试样为醋酸酯纤维制成的水刺非织造布，醋酸酯的密度为 1.36 g/cm3。

则试样在电容器中的体积分数Vf为

水的体积分数Vw为

2 实验数据与分析

试样应被看成是非织造布-水-空气的三相集合体，由于空气的介电常数接近真空的介电常数，可以将试样看作非织造布-水的两相集合体。

2.1 含水率与介电常数的关系

图2示出5片非织造布试样含水率分别为15.00%、12.77%、11.44%、8.97%、7.14%、5.76%及3.85%时的介电谱。可以看出非织造布-水两相集合体的介电常数随着测试频率的增大而减小，在低频段时，介电常数随着频率的增大而快速减小。在高频段时，介电常数随频率的变化幅度比较小。这种现象是由电容器内的材料和水产生介电弛豫现象而引起的[11]，由于偶极取向运动总是滞后于电场频率，当频率增加时，这种滞后会变得更加明显，因此在低频段，频率对介电常数的影响非常明显，而在高频段，频率对介电常数的影响变得不明显。同时由图2还可以看出，在相同频率下试样的介电常数随着含水率的增大而增大。在低频段，含水率越大，介电常数随频率变化越大，对于低含水率的试样，其介电常数随频率的变化不明显。在高频段，含水率对集合体介电常数的影响减弱。正如Donald等[12]指出的，当纤维的含水率接近于0时，介电常数与频率几乎无关。

图2 不同含水率试样的介电谱Fig.2 Dielectric spectra of samples with different moisture contents

2.2 非织造布体积分数与介电常数的关系

图3示出不同体积分数的干燥非织造布的介电常数，其中体积分数7.42%、6.04%、4.31%、2.89%、1.49%分别对应5、4、3、2、1片干燥非织造布的体积分数。可以看出干燥试样的介电常数随干燥试样的体积分数增大而增大，并且在低频段增大的幅度更大。

图3 干燥试样不同体积分数的介电常数Fig.3 Dielectric constant of different volume fractions of dried samples

由图3中选取出频率为1×106Hz和1 Hz时非织造布体积分数与其介电常数的数据绘制成图，如图4所示。可以看出在电场频率为1 Hz和1×106Hz时，干燥试样的体积分数与介电常数之间存在线性关系，但是1 Hz比1×106Hz时直线的斜率大，这是由于在低频段介电常数增加的速率比高频段大产生的。

对图3中所有频率点干燥非织造布体积分数与其介电常数之间的关系进行拟合，结果如表1所示。可以看出，干燥非织造布的体积分数与其介电常数之间在所有的频率下均为线性关系[13]，并且随着频率的降低，直线斜率不断增加，同样体积分数增量导致的介电常数其增加值更大。

图4 干燥试样1 Hz与1×106 Hz频率下试样体积 分数与介电常数关系Fig.4 Relationship between volume fraction and dielectric constant of samples at 1 Hz and 1×106 Hz in dry samples

表1 不同频率时干燥试样的体积分数 与介电常数的关系Tab.1 Relationship between volume fraction and dielectric constant of sample at different frequencies

2.3 水体积分数与介电常数关系

将试样看作非织造布-水的两相集合体，假设集合体的介电常数由2部分组成：一部分为非织造布；另一部分为水。即ε=ε1+ε2，其中ε1为试样中水的介电常数，ε2为试样中非织造布的介电常数。2.2中已知ε2与非织造布体积分数的关系，将集合体与非织造布的介电常数作差得到试样中水的体积分数与其介电常数的关系，如图5所示。可以看出，在高频段集合体的介电常数对水的体积分数不敏感，而在低频段集合体的介电常数对水的体积分数非常敏感且随着水的体积分数的增大而增大。在水的体积分数较小时，介电常数对电场频率也不敏感。这是因为试样中少量水分会与非织造布的醋酸酯紧密结合形成结合水，这部分水对电场频率不敏感，几乎不随电场频率的变化而变化。

图5 试样中水的体积分数与介电常数的关系Fig.5 Relationship between volume fraction of water and dielectric constant in samples

为对比高频段与低频段水分的体积分数对其介电常数影响的差异，图6分别示出1 Hz、1×106Hz时水的体积分数与其介电常数之间的关系，均为指数函数关系。可看出，介电常数随着水的体积分数增大而增大，当水的体积分数比较小时，介电常数增大速率非常小，随着水的体积分数增大，介电常数也快速增大。这是因为当水的体积分数比较小时，试样中的水分主要以结合水的形式存在，这部分水分对介电常数的影响比较小，当水的体积分数继续增大，试样中开始有自由水出现，这部分水分会对介电常数产生很大的影响。

图6 水的体积分数与介电常数的关系Fig.6 Relationship between volume fraction of water and dielectric constant at 1 Hz (a) and 1×106 Hz (b)

2.4 含水率与单位质量介电常数变化率关系

图7分别示出试样在1×106Hz与1 Hz时含水率与介电常数的关系。可以看出，试样的含水率与其介电常数在1×106Hz和1 Hz时都存在着明显的指数函数关系。设

E=(εl-εh)/m

(3)

式中：E为单位质量介电常数变化率；εh为试样在高频(1×106Hz)时的介电常数；εl为试样在低频(1 Hz)时的介电常数；m为试样的湿态质量，g。

图7 含水率与试样介电常数的关系Fig.7 Relationship between water content and dielectric constant of sample at 1×106 Hz (a) and 1 Hz (b)

将图7中的数据根据式(3)求出得到含水率与单位质量介电常数变化率的关系，见图8。可以看出E与含水率之间存在着明显的幂函数关系。在含水率比较低(4.37%～6.45%)时，E的变化幅度比较小，变化速率也较小。随着样品含水率的继续增大(7.84%～15.44%)，E的变化幅度越来越大，变化速率也越来越快。醋酸酯纤维的公定回潮率为6%～7%，此时醋酸酯纤维所对应的含水率为5.66%～6.54%。由此可以看出，当醋酸酯纤维非织造布的含水率低于醋酸酯纤维公定回潮率对应含水率时，单位质量介电常数变化率随含水率增长而增长的幅度比较小。随着含水率逐渐增大，单位质量介电常数变化率快速增大。

图8 含水率与单位质量介电常数变化率的关系Fig.8 Relationship between water content and rate of change of dielectric constant per unit mass

3 结 语

醋酸酯水刺非织造布的含水率对其介电常数有着很大的影响，在非织造布含水时其介电常数对电场频率比较敏感，在介电弛豫作用下非织造布-水两相集合体的介电常数随着电场频率的增大而减小。干燥状态下，非织造布的介电常数对电场频率的变化不敏感，其介电常数与非织造布的体积分数呈线性关系，且随非织造布的体积分数增大而增大。具有一定含水率的非织造布的介电常数可以认为是由非织造布和水2部分的介电常数组合而成，其中非织造布的体积分数与其产生的介电常数存在着线性关系，试样中水分的体积分数与其产生的介电常数存在着指数函数关系。在电场频率为 1 Hz 和1×106Hz 时，试样的含水率与试样的介电常数存在着指数函数关系。含水率与单位质量介电常数变化率之间存在着幂函数关系，单位质量介电常数随着含水率的增大而增大，且增长速率越来越快。在试样含水率小于公定回潮率所对应的含水率时，单位质量介电常数的变化幅度比较小，当试样的含水率大于公定回潮率所对应的含水率，单位质量介电常数的变化幅度会明显增大。