货物升降对叉车横向稳定性影响及控制策略研究

张之路, 肖本贤

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

随着物流产业的发展,叉车作为运输物料的重要设备,其应用领域越来越多,发展前景越来越大。不同于汽车等传统车辆,叉车由于存在货物升降的特殊性,对其稳定性评估需要考虑叉车载荷情况下货物升降导致的叉车合成重心变化对横向稳定性所造成的影响。为改善叉车在运行过程中发生倾覆及稳定性失控的风险,国内外研究工作者针对叉车的特殊性进行了大量的控制策略及控制器方面的技术研究。文献[1]建立了叉车防倾覆模型并设计了基于模型预测控制的防倾覆控制系统，保证了叉车的稳定性;文献[2]研究了叉车在过速转弯时最大速度、轮胎性能及重心位置等对于叉车横向稳定性的影响;文献[3]提出了利用小波网络动态逆内模控制实现对叉车主动后轮转向和直接横摆力矩解耦控制提升叉车状态跟踪和解耦控制;文献[4]基于提出的叉车制动转向工况半车动力学模型，对转向制动工况下的叉车进行最优控制并取得了良好的效果。

上述控制方法考虑了叉车合成重心对于叉车横向稳定性及纵向倾覆的影响,但并未考虑叉车在行驶过程中货物升降导致叉车合成重心动态变化对于叉车横向稳定性的影响。基于此,本文提出了一种新的考虑货物升降对于叉车横摆角速度和质心侧偏角影响的车辆模型,在上述模型的基础上提出一种基于简化混沌粒子群算法(simplified chaotic particle swarm optimization,SCPSO)的横向稳定性控制器,控制器利用SCPSO算法所具有的实时快速性来实现对理想横摆角速度和质心侧偏角的良好跟踪,最后利用Matlab/SIMULINK在双移线工况下对控制策略进行仿真评价分析并进行试验,仿真及试验结果验证了上述控制策略,改善了货物升降对叉车横向稳定性造成的影响,叉车在转弯条件下可以对货物进行升降而不会影响叉车稳定性,提高了叉车的工作效率。

1 叉车动力学模型及理想跟随模型

1.1 叉车动力学模型

考虑货物升降情况下,对叉车在x、y、z方向建立叉车动力学模型,如图1所示。

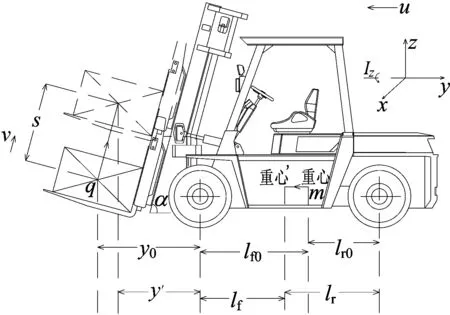
图1 叉车动力学模型

图1中,m为叉车自重;q为货物重量;lf0为叉车未加货物情况下重心距前桥中心线的距离;lf为考虑货物情况下重心距前桥中心线的距离;y′为货物经过t时间后重心距叉车前桥中心线水平距离;y0为初始情况下货物重心距叉车前桥中心线的水平距离;v为货物上升速度;α为叉车后倾角;u为叉车前进速度。定义kf、kr分别为前、后车轮的侧偏刚度。δf、δr分别为前、后车轮转角;β为整车质心侧偏角;γ为绕z轴横摆角速度。结合车辆二自由度模型[5]

及叉车合成重心变化模型

(2)

作如下假设:货物升降是一个相对独立的系统,只对叉车合成重心位置在y、z轴变化产生影响,对上升距离设定阈值以忽略合成重心在z轴变化造成的纵向稳定性影响。由此推出考虑货物升降情况下叉车横向稳定性模型,即

(3)

1.2 理想跟随模型

本文控制原理采用反馈控制,由上述叉车模型作为理想跟随模型,期望横摆角速度为:

(4)

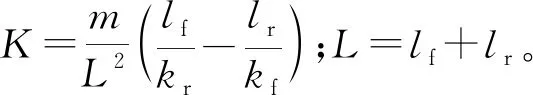
(5)

其中,Gr为前轮转向汽车横摆角速度对前轮转向角的稳态增益。

从叉车行驶的安全角度考虑,无论前轮转角输入为多少,质心侧偏角应恒等于0,这样转弯时车辆纵轴线与行驶方向保持一致,便于驾驶,按上述思想,期望质心侧偏角为:

βd=kεδf

(6)

其中,kε为比例增益,在此取0。

2 叉车横向稳定控制系统设计

2.1 叉车横向稳定性控制原理

由于单独采用差动制动会对叉车的横摆运动造成较大的冲击,单独采用四轮转向控制在侧向加速度较大情况下控制效果不佳。因此采用四轮转向和差动制动联合控制,既可以利用四轮转向分担一部分的横摆力矩,减少差动制动所造成的冲击,也弥补了四轮转向单独控制时的缺点。基于此,本文采用的控制结构如图2所示。

图2 叉车横向稳定性控制原理框图

控制系统以货物下降速度v、前轮转向角δf,货物重量Q作为输入量,以横摆角速度β、质心侧偏角γ作为控制输出量。横向稳定控制器以理想横摆角速度、质心侧偏角和实际横摆角速度、质心侧偏角偏差作为输入,输出后轮补偿角和附加横摆力矩,并通过差动制动分配制动力矩来实现叉车稳定性控制。

在文献[6]基础上,结合(3)式给出的叉车模型,四轮转向和差动制动联合控制的叉车模型微分方程如下:

(7)

其中,MBS为附加横摆力矩;δr为后轮补偿角。

差动制动轮选取规则见表1所列[7]。

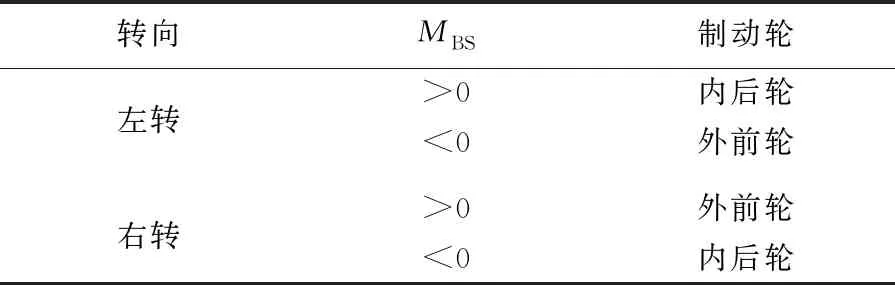
表1 制动轮选取规则

2.2 基于混沌的简化粒子群算法

粒子群算法(particle swarm optimization,PSO)是一种模拟鸟群和鱼群觅食过程中迁徙和聚集行为的进化算法,该算法赋予每一粒子位置和速度2个特性[8]。粒子位置作为待解决问题的可能解,目标函数(利用粒子的位置坐标求解)作为适应度来衡量群体中每个粒子优劣的标准。利用位置和速度2个特性,粒子通过跟踪个体极值与全局极值来不断更新自己在解空间中的位置,从而找到问题的最优解。目前常用的更新粒子速度和位置的公式如下:

(8)

其中,t为当前迭代次数;P为粒子当前位置;V为粒子的速度;ω为惯性权重;c1、c2为学习因子;r1、r2为[0,1]上产生的随机数;Pbest为粒子个体最优解;Gbest为全局最优解。

传统的粒子群算法需要不断更新个体历史最优解和全局最优解,并以此来更新当前粒子位置,本文舍弃个体历史最优解Pbest以加快粒子群迭代速度,简化的PSO算法迭代公式如下:

(9)

其中,ω为惯性因子;c为学习因子;r为[0,1]上产生的随机数。采用(9)式加快了粒子迭代速度,但多样性缺失导致粒子更易陷入局部最优解,因此引入混沌理论来优化该问题,具体操作为通过计算粒子群的适应度方差来判断粒子群粒子是否陷入局部最优并通过混沌来更新陷入局部最优的粒子群位置,相应的算法流程如图3所示。

基于本文的控制器要求,目标函数选取为minf(xi)=K1|β-βd|+K2|γ-γd|。β、γ为其中关于后轮补偿角δr和附加横摆力矩M的函数;K1、K2为归一化因子,可分别选取为K1=1/βmax,K2=1/γmax。混沌初始化粒子群位置及更新粒子群采用立方映射，并将混沌区间[0,1]映射到对应变量的取值区间。

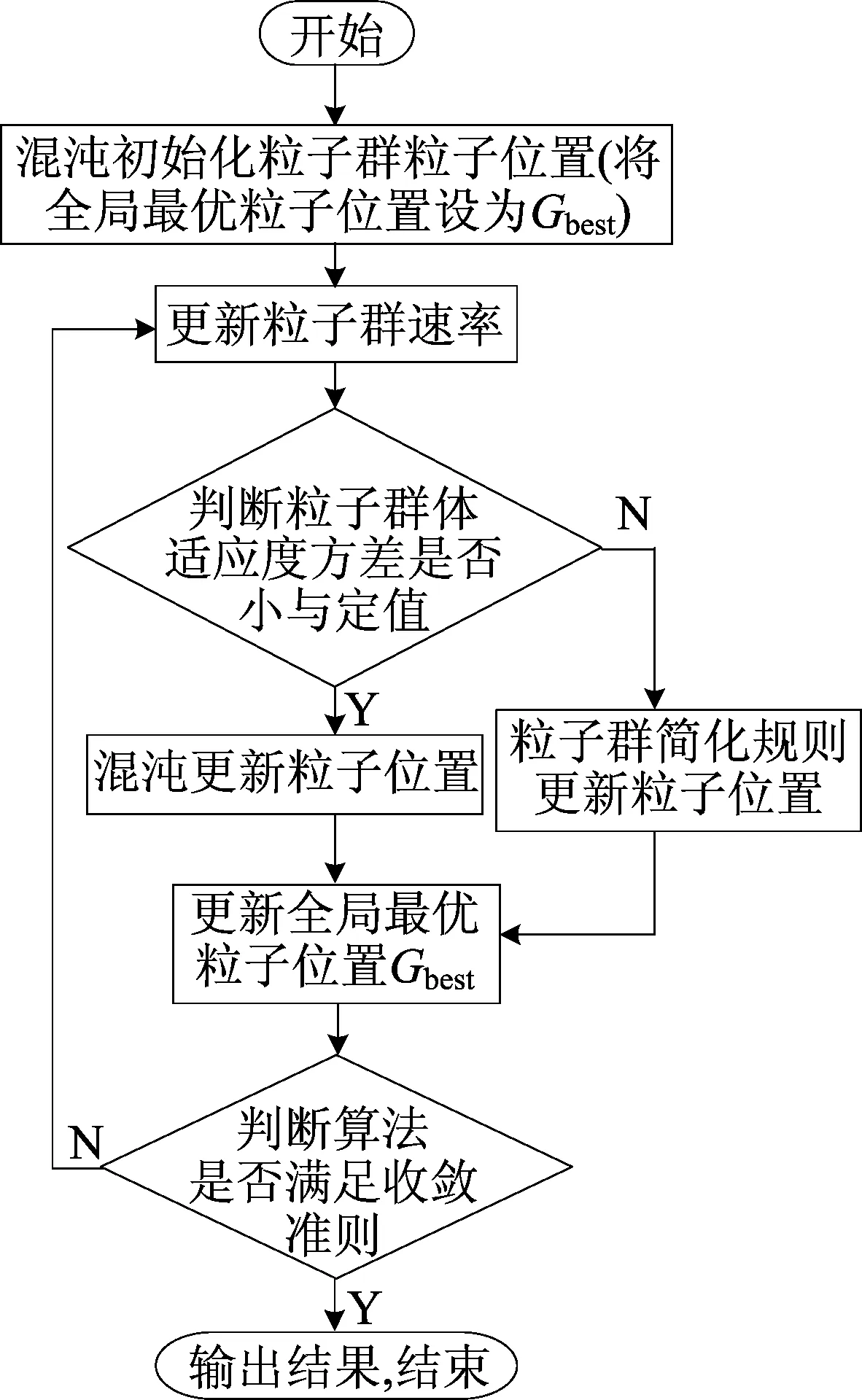
图3 基于混沌的简化粒子群算法流程

立方映射表达式为:

(10)

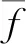
(11)

考虑本文叉车横向稳定性控制系统参数随着举升系统的运行实时变化,相比准确性,实时跟踪性更为重要,因此采用上述算法比一般传统算法更符合本文的控制要求。

为验证算法的有效性,本文分别比较了基本PSO算法、基于自适应惯性权重的均值粒子群优化算法(a mean particle swarm optimization algorithm based on adaptive inertia weight, MAWPSO)与SCPSO分别在不同适应度函数下的性能与效果。Griewank函数和Rastrigin函数是用来测试算法寻优性能的常用函数,它们具有多个局部最优解,可以用来测试算法的收敛速度及跳出局部最优解的能力。选取PSO学习因子c1=1.5,c2=1.5,惯性权重ω=0.8;CSPSO学习因子c=1.48,惯性权重ω=0.8搜索空间维数为10维,初始化群体个体数目为30,最大迭代次数为100。测试效果如图4所示。

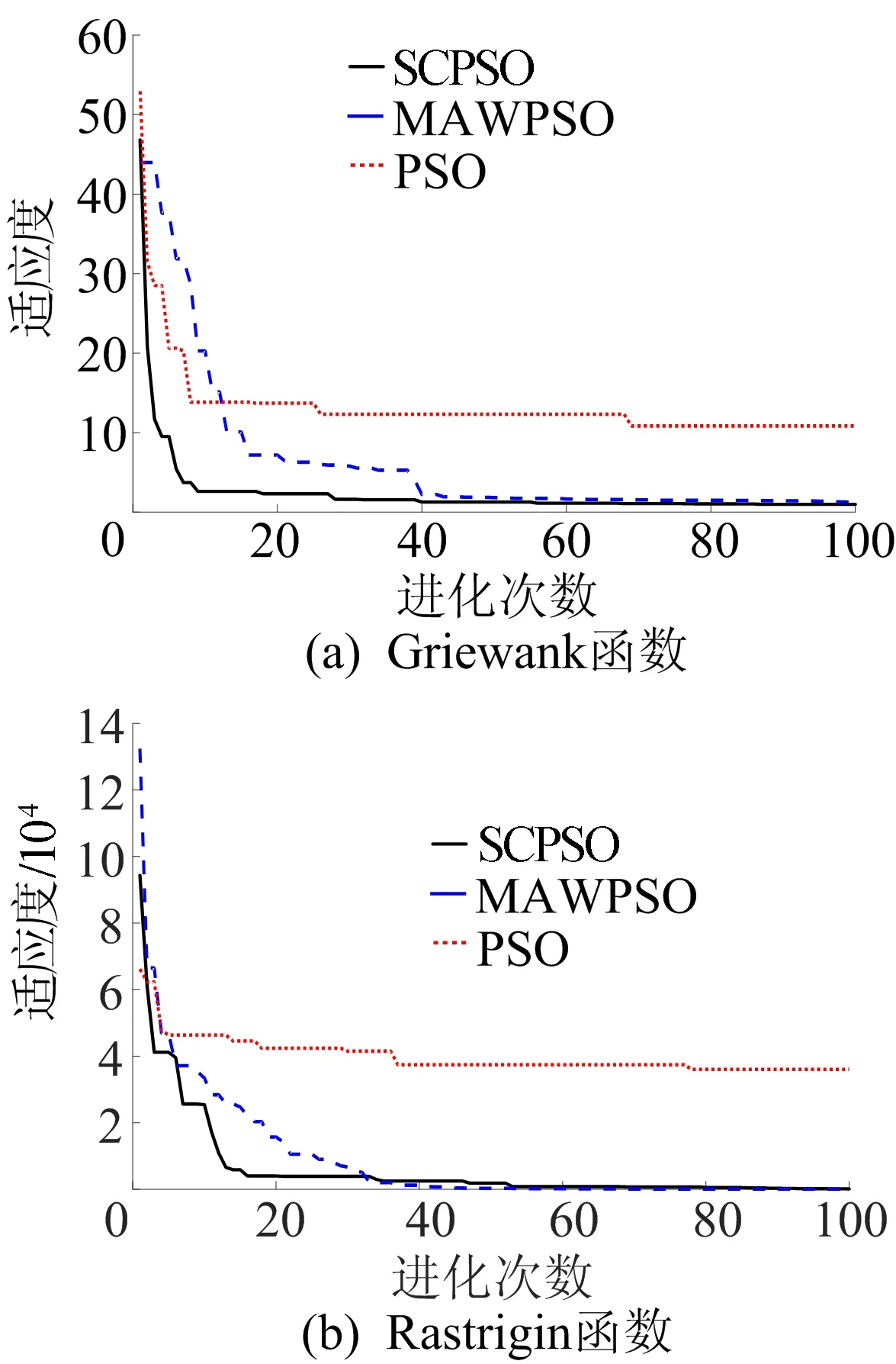
图4 Griewank、Rastrigin函数测试结果

从图4可以看出,本文提出的SCPSO算法虽然在精度上相对于MAWPSO算法没有太大的优化,但是在算法的快速性上明显优于MAWPSO算法,而相比于传统的PSO算法又具有很好的跳出局部最优解的能力,在进化至第40代左右就能进入符合控制要求的误差范围,能够很好地满足本文叉车横向稳定性控制要求,在满足一定精度的条件下使叉车质心侧偏角与横摆角速度快速跟随理想值。

3 仿真与试验分析

为验证本文提出的叉车理想模型和控制策略的正确性及有效性,采用Matlab/SIMULINK进行仿真,叉车模型具体参数设置见表2所列。

表2 叉车仿真模型参数

3.1 双移线换道工况分析

双移线换道工况是用来测试车辆横向稳定性的常用工况[9],仿真试验时选用MacAdam驾驶员模型模拟方向盘的转角输入,最大转向角为0.13 rad,如图5所示。

图5 转向盘转角输入曲线

设定叉车行驶速度为10 km/h,分别在货物升降速度为0、0.15、0.25 m/s条件下进行仿真,结果如图6所示,从图6可以看出,双移线工况下随着货物上升速度的增大,横摆角速度与质心侧偏角也相应增大,在4.9 s左右达到峰值,这是由于货物合成重心后移速度越快,相应地横向稳定性会越差[10]。因此,有必要设计控制器来改善由于货物升降对叉车横向稳定性的影响,为能够实现良好地对理想模型的跟踪,采用上述基于CSPSO算法的稳定性控制器。

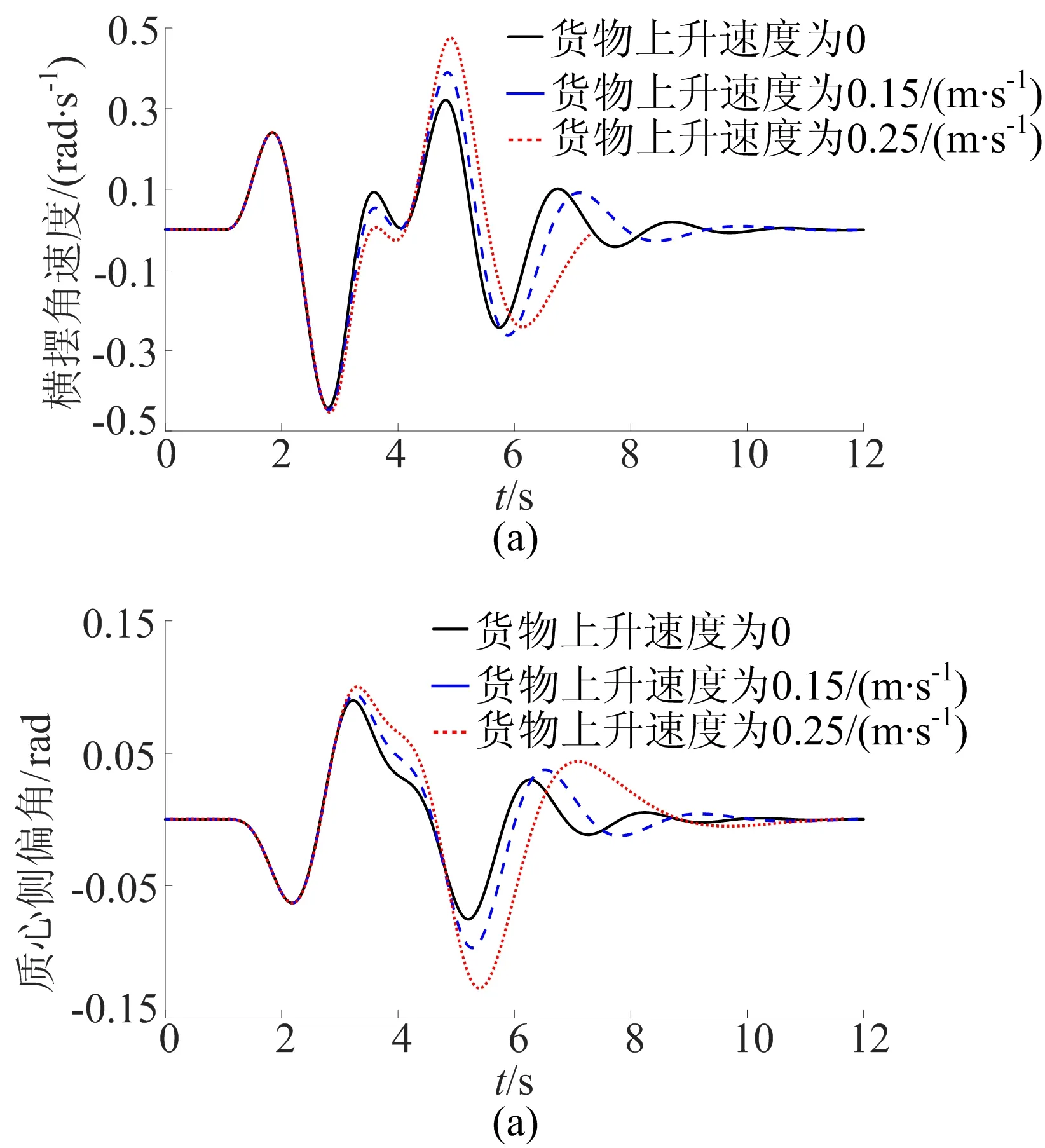
图6 双移线工况下叉车不同速度货物升降仿真结果

对上述双移线工况采用本文所提出的控制策略并与基于PSO算法控制器进行比较,其中,CSPSO算法中参数设定分别为σ2=0.01,βmax=0.5,γmax=0.13,c=1.48,ω=0.8,PSO算法中参数设定分别为c1=1.5,c2=1.5,ω=0.8,初始化种群数目为30,迭代次数设置为100,具体仿真结果如图7所示。

从图7可以看出,通过控制器的优化作用,叉车在双移线工况下横摆角速度及质心侧偏角具有明显的改善,相比于传统PSO控制器,SCPSO控制器具有更好的跟随性能。

图7 双移线工况下CSPSO控制横摆角速度和质心侧偏角响应曲线

无控制状态下,横摆角速度在2.8 s时达到峰值0.5 rad/s,质心侧偏角在5 s时达到峰值0.11 rad,在实际叉车行驶过程中,已明显处于失稳状态。采用传统PSO控制,质心侧偏角在2.6 s时达到峰值0.053 rad;采用SCPSO控制,质心侧偏角在4 s时达到峰值0.03 rad,且相比于传统PSO控制器,横摆角速度对理想值的跟随性能更好,系统的动态控制效果更好,整车稳定性得到很大提升,改善了叉车举升系统运行时叉车横向稳定性变差的缺点。

3.2 双移线换道工况试验分析

试验采用电动平衡重叉车,试验平台如图8所示。

图8 试验平台

采用上述基于SCPSO算法控制器及传统基于PSO算法控制器进行实地叉车试验分析以测试其在双移线工况下车辆稳定性能。记录叉车实验时的横摆角速度、前轮转角和车速,按照上述控制策略对理想横摆角速度进行跟踪,以改善叉车货物升降情况下转向过程稳定性。试验在较好路面下进行,分别比较施加控制和未施加控制的试验结果。

设定叉车行驶速度为10 km/h,货物上升速度为0.25 m/s,控制器参数设定与3.2节相同,未施加控制与施加PSO及SCPSO控制试验结果如图9所示。

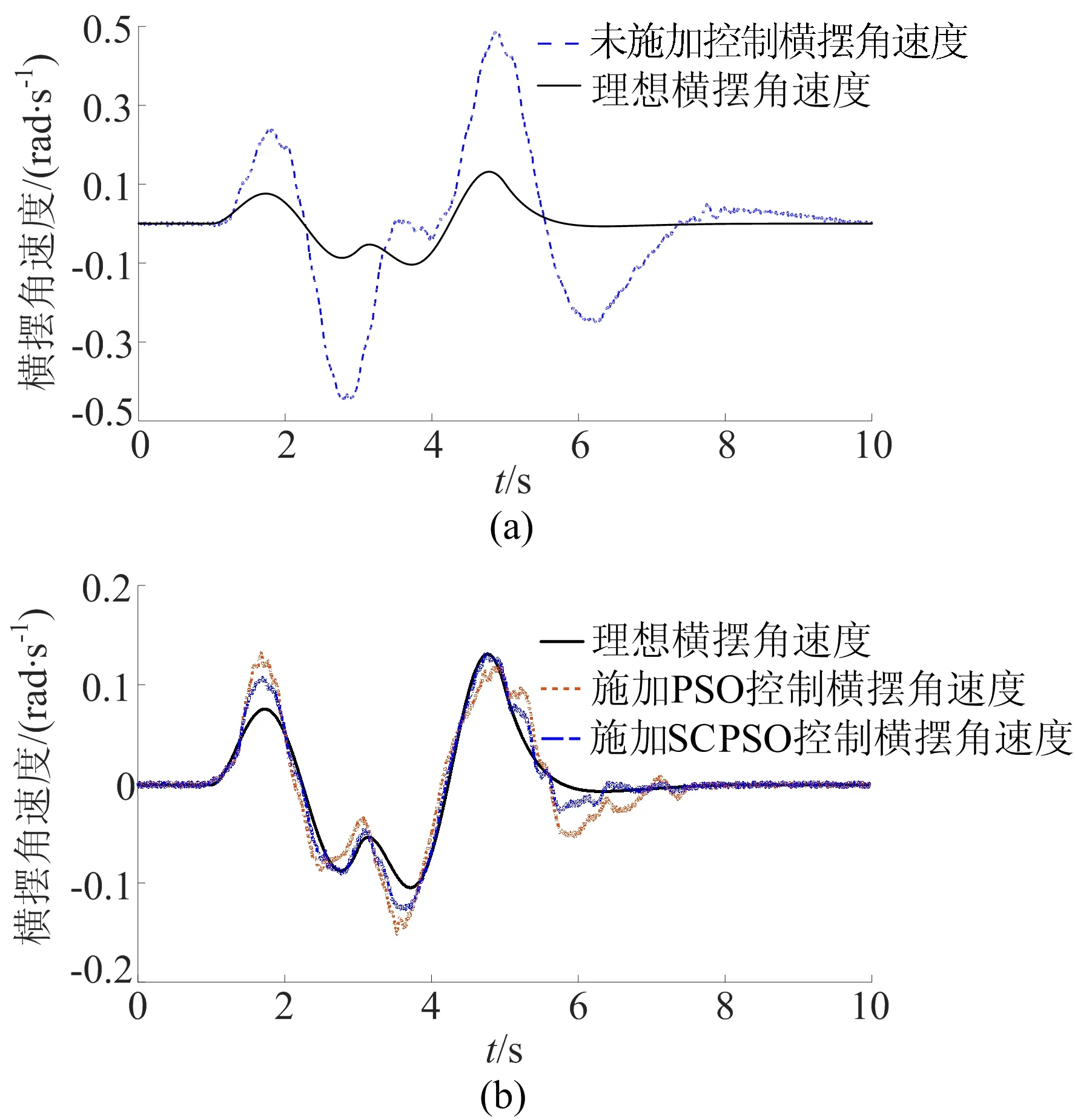
图9 双移线换道工况试验

通过分析可知,在未施加控制时,横摆角速度由于货物上升明显增大,在4.8 s达到峰值0.48 rad/s,此时,车辆已经接近不稳定状态,提升了驾驶员的操作难度。与传统PSO控制相比,采用SCPSO控制后,横摆角速度更接近于理想值,提高了车辆在转弯过程中的稳定性。

试验结果表明,本文SCPSO算法的横向稳定性控制器能够改善叉车在转弯过程中由于货物升降造成稳定性变差的影响。

4 结 论

本文首先在车辆模型的基础上,结合叉车举升系统运行特点,提出了一种考虑叉车货物升降的横向稳定性模型;其次提出了一种SCPSO算法的横向稳定性控制器,该算法在原始PSO算法基础上简化了粒子群位置寻优公式,并加入混沌理论改善算法易于陷入局部最优解的缺点,通过与基本PSO算法、MAWPSO算法比较,验证了该算法在快速性方面得到显著提升,符合本文系统需要快速跟随的特性;最后通过双移线工况下仿真及试验结果,验证了提出的控制策略具有较强的瞬态响应能力和动态控制性能,抑制了横摆角速度的波动,使得质心侧偏角接近于期望值,取得了良好的转向特性,叉车在货物升降情况下转向稳定性得到了明显改善,提升了叉车工作效率。