异型钢结构制作及安装精度控制技术分析

2021-01-05唐寅兵

中国金属通报 2020年17期

唐寅兵

（中国水利水电第八工程局有限公司，湖南长沙 410004）

钢结构构件的体积比较大、结构设计上也比较复杂，具有更好的抗震性能和可靠性，如今，在人们的日常生活和现代工业生产中发挥着十分重要的作用，也被广泛应用到建筑、工业厂房、机场以及大型海洋石油平台等领域中[1]。在异型钢结构的制作以及安装过程中，通常采用从下到上的建造方法，导致钢结构的施工时间变长，因此，在现代工业领域中，异型钢结构分层同时建造、最后以整体的方式组装早已经成为现代工业发展的主要流行趋势[2]。

异形钢结构在制作过程中，上层与下层甲板、钢结构的层间立柱都存在一定的制造误差，为了保证异型钢结构在制作和安装过程中符合精度要求，需要适当调整异型钢结构的定位位置和安装误差[3]。在异形钢结构的施工过程中，通过调整甲板片所处的位置，来判断异型钢结构所处的位置是否满足其制作和安装精度要求，还要将甲板片与安装位置吊离，校正甲板片和立柱的同时，还要经过反复的吊装和测量，直到异型钢结构的制作和安装精度满足技术要求[4]。对于异形钢结构来讲，可以通过事先装配的方式，减少安装位置上的返修，提高异型钢结构制作以及安装的精度，但是对于异形多层钢结构而言，事先装配是很难实现的，因此，可以看出异型钢结构制作及安装精度控制是异形钢结构在整体组装方面的一个技术难点。

1 异型钢结构制作及安装精度控制技术设计

1.1 钢结构制作及安装变形的有限元分析

采用ANSYS软件对各层钢结构安装变形进行分析计算。钢结构具有结构复杂、构件众多的特点，细长杆结构是其主要结构[5]。针对钢结构的规模及以构件作为主体结构的特点，一般采用梁单元进行建模。梁单元是一种基于一维简化的三维结构，采用梁轴变形运动代替实体变形运动；相对于实体单元和板壳单元，计算效率有很大提高，因此，采用APDL语言对ANSYS进行参数化建模，实现钢结构制作及安装变形的有限元分析。

假设钢结构的施工区域为一块强夯土区域，根据施工场地的岩土勘察报告，将强夯土地基划分为四个层次，每一个层次的参数如表1所示。

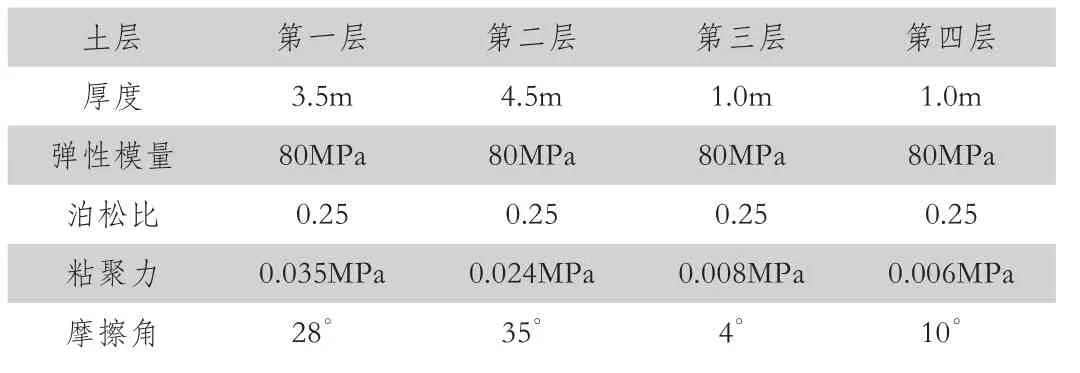
表1 钢结构施工场地强夯地基的各层参数

将SRID 92和SRID65应用到强夯地基建模过程中，利用Solid65能较好地模拟钢结构施工土体的非线性特征，而Solid92能较好地划分施工场地的不规则网格。用Drucker-Prager理想弹塑性模型计算土料的特性，由内摩擦角φ、膨胀角β和粘聚力℃定义，其中β是由φ决定的。钢结构施工地基的约束条件为：底部约束垂直方向，不允许基础横向位移[6]。

经过钢结构制作及安装变形的有限元分析，钢结构在前三层甲板片安装时经常会出现比较大的变形，因此，在施工过程中，需要在设备的下方增加一个临时的支撑点，以此来加固钢结构[7]。

根据钢结构的规模及特点，采用APDL语言对ANSYS进行参数化建模，结合钢结构施工场地强夯地基的各层参数，对钢结构制作及安装变形进行了有限元分析，接下来通过建立异形钢结构制作及安装精度控制模型，来消除脉冲频率对异型钢结构制作及安装精度的影响。

1.2 建立异型钢结构制作及安装精度控制模型

异型钢结构在制作及安装过程中，采用计数法来建立精度控制模型，计数法的原理是采用相同的自变量对钢结构的主轴转动频率进行离散化变形，钢结构制作设备的主轴转动频率为f(t )，钢结构安装设备的转轴频率为f(s )，设备的转动角度为θ，设备的行进步数为s ，那么异型钢结构制作及安装精度控制阶段在离散化变形前后的f(s )-f(t )模型如图1所示。

从图1的模型中可以看出，f(t )异型钢结构经过离散化变形后，将变得更加紧凑，说明异形钢结构制作及安装精度控制有所加强。在控制过程中，精度控制的时间间隔是越来越小的，这样可以有效避免精度控制指令由于设备转速比较低而出现失效现象。

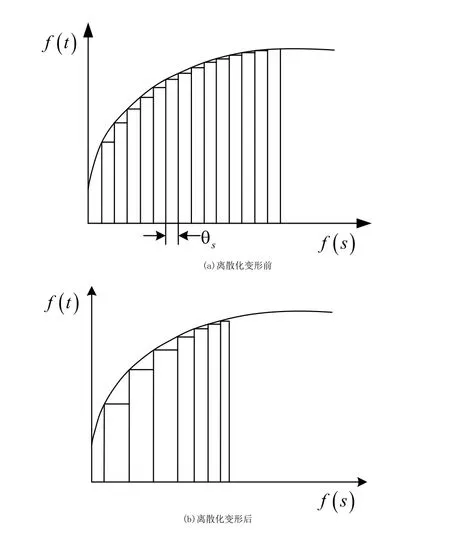
图1 离散化变形前后的f(s )-f(t )模型

采用函数来表示异形钢结构制作及安装精度的控制模型，将脉冲设为自变量，异型钢结构制作及安装过程中产生的脉冲信号，都会使钢结构施工设备产生转动和步数[8]。假设异型钢结构在制作和安装中一共产生N 个脉冲信号，采用k 表示脉冲当量，设备的转动角度可以表示为θ=Nk ，那么制作及安装设备逆向转动速度与转动角度之间的函数关系为：

根据设备逆向转动速度ω与转动角度θ之间的函数关系，可以求出设备逆向转动速度ω 对异型钢结构制作及安装中负载的运动模型，表示为：

其中，J 表示负载的转动惯量，KT表示负载的转矩因子，T0表示磁力转矩。

初始化异型钢结构的制作及安装工作，设精度的控制是从0时刻开始的，分析图1可以求解得到异型钢结构负载运动模型的解，将其表示为：

以上通过对异型钢结构在制作及安装精度控制阶段进行离散化处理，得到了离散化变形前后的模型，根据制作及安装设备逆向转动速度与转动角度之间的函数关系，求出逆向转动速度对异型钢结构制作及安装中负载的运动模型，利用异型钢结构制作及安装精度控制模型的函数，建立了异型钢结构制作及安装精度控制模型，接下来通过异型钢结构制作及安装精度控制流程，来实现异型钢结构制作及安装精度的控制。

1.3 控制异形钢结构制作及安装精度

基于异型钢结构制作及安装精度控制模型，需要采用细分驱动的控制方法，来实现异型钢结构制作及安装精度的控制。细分驱动控制的原理如图2所示。

图2 细分驱动控制原理图

细分驱动技术是利用分片驱动，将制造安装设备的旋转角度划分为小范围进行控制的一种技术。该控制技术的控制效果显著、稳定性强，可有效减少制造及安装设备中低频振荡对精度控制指令的影响[9]。利用单片机控制器来调用滤波电路，消除制造安装设备旋转信息中的滞后角，实现细分驱动控制。滤波器电路可以去除的最大噪声对比表见表2。

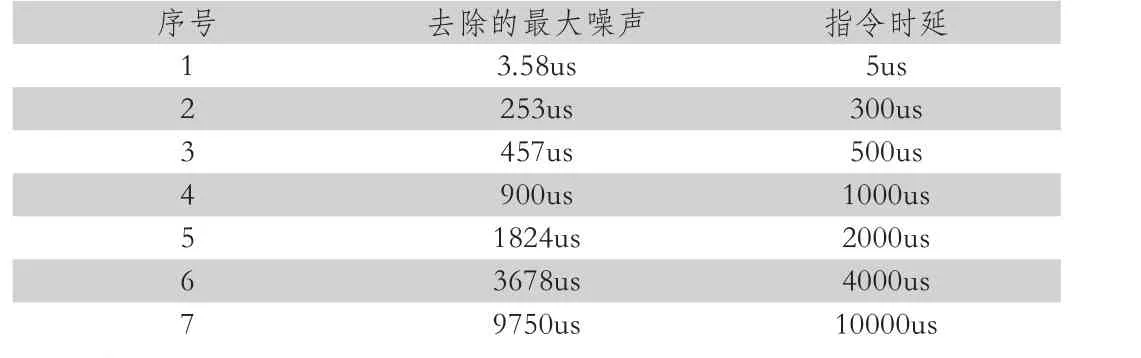
表2 滤波器电路可以去除的最大噪声对比表

消除了制作安装设备的滞后角，可以实现对制作及安装设备旋转信息的双向操作。滤波电路将制造安装设备无迟滞角的旋转信息反馈给单片机控制器，通过细分驱动控制，将制造安装设备的旋转角度细分为N个区域进行精度控制，得到N个交流电信号。将N个交流电讯信号进行电压放大，并将电压放大传送至存储器；另一方面，滤波电路需要在制造安装设备的旋转信息的MCM电路中进行模数转换，然后进行差分放大，最后传送到存储器[10]。

以上提出的精度控制方法对制作及安装精度的控制结果，将与细分驱动控制指令的结果呈现出一种正弦规律或余弦规律，那么异型钢结构制作精度控制指令信号和安装精度控制指令信号分别为：

综上所述，通过对钢结构制作及安装变形进行有限元分析，建立了异型钢结构制作及安装精度控制模型，结合异型钢结构制作及安装精度控制流程设计，实现了异型钢结构制作及安装精度的控制。

2 实验对比分析

2.1 异型钢结构制作及安装精度控制速度对比测试

实验以脉冲频率为自变量，分别采用提出的精度控制技术、传统精度控制技术测试了异型钢结构制作及安装精度控制速度情况，实验结果如表3所示。

表3 精度控制速度对比结果

从表3的实验结果可以看出，采用传统精度控制技术来控制异型钢结构的制作及安装精度时，由于该技术缺少对钢结构制作及安装变形的有限元分析，导致钢结构的稳定性变弱，从而减慢了精度控制速度；采用提出的精度控制技术来控制异型钢结构的制作及安装精度时，该方法不仅对钢结构制作及安装变形进行了有限元分析，还建立了精度控制模型，使得异型钢结构制作及安装精度的控制速度明显比传统精度控制技术快。

2.2 异型钢结构制作及安装精度控制误差对比测试

实验以脉冲频率为自变量，分别采用提出的精度控制技术、传统精度控制技术测试了异型钢结构制作及安装精度控制误差情况，实验结果如表4所示。

表4 精度控制误差对比结果

从表4的实验结果可以看出，在异型钢结构制作及安装精度控制误差方面，提出的精度控制技术明显优于传统精度控制技术，经计算，提出的精度控制技术得到的控制误差平均值为8.743 kHz，而传统精度控制技术得到的控制误差平均值为353.63 kHz，因此，可以得出提出的精度控制技术可以有效减小异型钢结构制作及安装精度的控制误差。