基于多变量混沌时间序列的航班运行风险预测模型
2021-01-04王岩韬李景良谷润平
王岩韬,李景良,谷润平
中国民航大学空管学院,天津 300300
近年不安全事件表明,民航工作高质量发展依赖于航班运行风险防控能力的提升[1].针对航班运行风险影响因素繁杂、随时间变化、等级界定困难等问题,欧美国家最早从1991年开始航班风险评价研究[2].从近年研究成果看,研究理论和手段仍使用事故树等传统方法[3-4].而在实践方面,自2007—2012年间美国、加拿大民航局研发了Flight risk assessment tool (FRAT)[5]、RA check[6]等飞行风险评估工具后,至今未有可信的使用报告和精度分析;除此之外,近年也未见其他突破.在国内,航班风险评估研究最早从1999年起步[7],而后王岩韬等[8-9]建立了具有指导性、实用性的航班运行风险评估体系,并运用多算法协作的方式将航班风险分类正确率提高至95%.对于民航非动态风险评估,上述研究已取得较好成果.但将前续成果应用于民航一线运行后发现,航班评估技术只能做到随航班要素快速变化而变化,评估结果代表已有状态,而风险管控工作需要时间提前量,因此风险预测技术才是风险防控实质所亟需.
2012年,欧盟开展航空运行主动性安全管理项目(Proactive safety performance for operations,PROSPERO),旨在通过对航空运输系统的风险主动预测,降低人为差错和空中交通事故率,但详细方案和结果报告一直未见报道,并且最新消息表明该项目已于2015年戛然而止[10].2018年Lalis等[11]使用线性回归模型和ARMA模型对航空安全绩效指标进行预测,但以月为单位的、本身就波动很小的时间序列严重削弱了其实用价值.2019年,Zhang与Mahadevans[12]融合支持向量机和深度神经网络两种算法应用于航空风险预测中,对单一事件预测精度达到了81%,但其过程实质上与风险评估类似,预测周期过短,预测能力不足.在国内,王岩韬团队于2019年提出了基于动态贝叶斯网络的航班运行风险预测模型[13],但该模型主要针对单个航班的进近、着陆阶段的风险预测,在预测周期很短的情况下精度达到了80.4%,无法体现航空公司的整体运行状况.由上,航班风险预测相关研究较少,至今缺乏精度较高的技术和方法,是民航安全领域尚未有效解决的关键问题之一.
深入分析其他领域的研究成果,发现多变量混沌时间序列预测方法是一种较好的短期预测技术,早期应用于经典的混沌序列中,证明了其比单变量预测更优[14-16].近年来,该方法广泛应用于工程领域,典型研究成果包括:2013年,侯公羽等[17]对煤矿斜井的盾构小时施工风险进行预测,均方根误差(Root mean square error, RMSE)为 0.4754;2016年,钟仪华等[18]对油田日产油量进行预测,均方根误差为0.0061;2017年,杜柳青等[19]对数控机床的日运动精度进行预测,均方根误差低于0.02;2018年,张淑清等[20]对电力日负荷进行预测,平均误差为0.813%;2018年,黄发明等[21]对滑坡的月波动项位移进行预测,均方根误差为23.71.上述工程应用均表明多变量混沌时间序列预测方法具有良好的预测效果.
由上,本文首先对运行数据时间序列进行混沌识别和相空间重构;然后,采用基于奇异值分解(Singular value decomposition, SVD)的主成分分析(Principal component analysis, PCA)法对相空间进行降维处理;进而,构建极限学习机(Extreme learning machine, ELM)、RBF神经网络、回声状态网络(Echo state network, ESN)和Elman神经网络4种风险预测模型,采取迭代方式进行风险预测;最后计算并分析不同模型的预测精度,判断其实践操作价值,旨在构建一种精度较高的航班运行风险预测方法,
1 航班运行风险时间序列及混沌特征识别
1.1 航班运行风险
“风险”一词最早仅代表客观的危险,狭义风险是指损失的不确定性,如工程建筑风险关注人员伤亡和设备损失;而广义风险强调表现的不确定性,如经营风险关注未来市场走向,如金融风险关注收益变化.“风险”最受认可的定义是由Coleman与Marks于1999年提出的,风险是结果严重程度和发生概率的综合[22].国际民航组织(ICAO)附件19中,延用了此定义,风险为某一危险源预计产生的可能性与严重性相乘,并以风险矩阵划分等级.如表1,绿区为可接受风险,即航班可以正常执行;红区为不可接受风险,即航班不可执行;而黄区需要进行有效风险缓解后,航班才可执行.
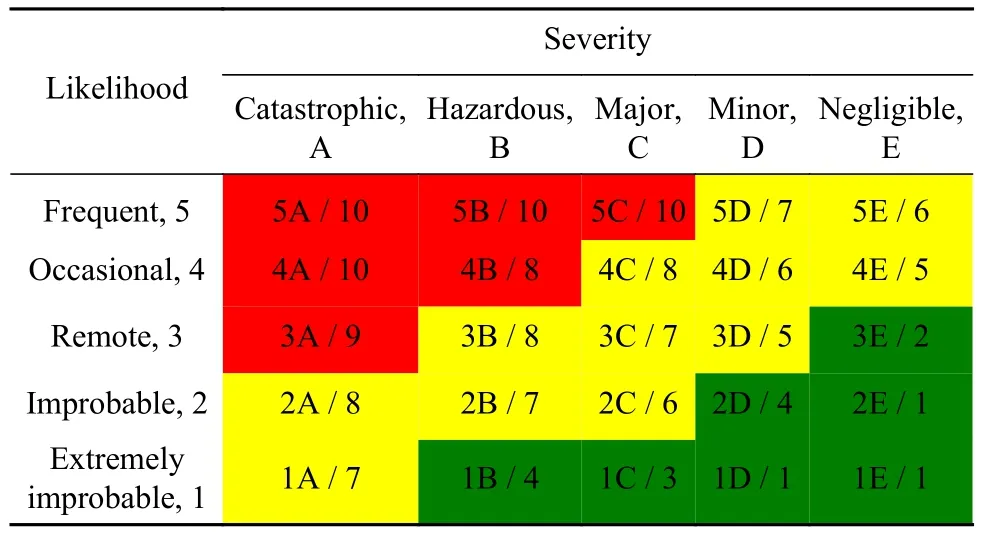
表1 ICAO风险矩阵与中国民航局(CAAC)风险值Table 1 ICAO risk matrix and CAAC risk value
但是在使用风险矩阵评判航班风险等级时,存在两个问题:①对于中国民航,任一人员伤亡、飞机损伤报废都无法接受,风险严重程度无法如金融行业等以金钱数字衡量;②根据《2019年民航机场生产统计公报》,我国持续安全记录已达112个月、8068×104h,而2019年航班已达1166万架次,事故、事故症候、不安全事件等发生概率接近极小值.
因此,为了解决风险矩阵的半定量化,进而发展风险评估与预测技术,民航局于2015年颁布《航空承运人运行控制风险管控系统实施指南(AC-121-FS-2015-125)》以政府指导的方式量化了风险,经实践多年已验证有效.其中,将风险矩阵中1E~5A转化为数字1到10,即风险数值化,如表1.该体系具有一定科学性,应用于数值化评估与预测时存在两个问题:①尚有少量的半定性/半定量和定性指标,需要依赖专家判断;②部分指标不具备可预测性,如人因和航空器类指标是不含时间维度特性的.
1.2 运行数据选取
由上,延续AC-121-FS-2015-125中对风险评定方式,使用可定量的数据来源.提取国内某大型航空公司风险管控系统和航空安全系统中风险源指标,统计2016—2018年连续以天为单位的航班数据,形成航班运行风险数据项1096组,数据类型和数据样本见表2和表3.
首先,处理15个风险项的数据,使用SPSS软件,取置信区间95%,使用SNK法和Dunnet-t法对数据列做多个均数多重比较,检验结果概率均小于0.05,说明数据间具有独立性;然后,再经飞行、运控、机务、安监等联合专家组检验,确认数据可信,故作为后续计算的标准样本.
1.3 混沌识别
根据航班运行风险数据样本,分别构建A1~A15和总风险时间序列,其中总风险时间序列如图1.采用Wolf法计算,结果表明总风险时间序列具有混沌特征,同理对15个风险源时间序列进行混沌识别,计算结果见表4.
从表4可见,16个风险序列均满足 λ>0,具有混沌特征.因此,首先通过对总风险时间序列进行单变量混沌预测,得到未来1 d的相对误差均值(Mean absolute percentage error, MAPE)为 21.33%.发现单一序列输入,不足以构建精准模型.故后续采用多变量时间序列增加输入,通过15个风险源序列预测总风险.
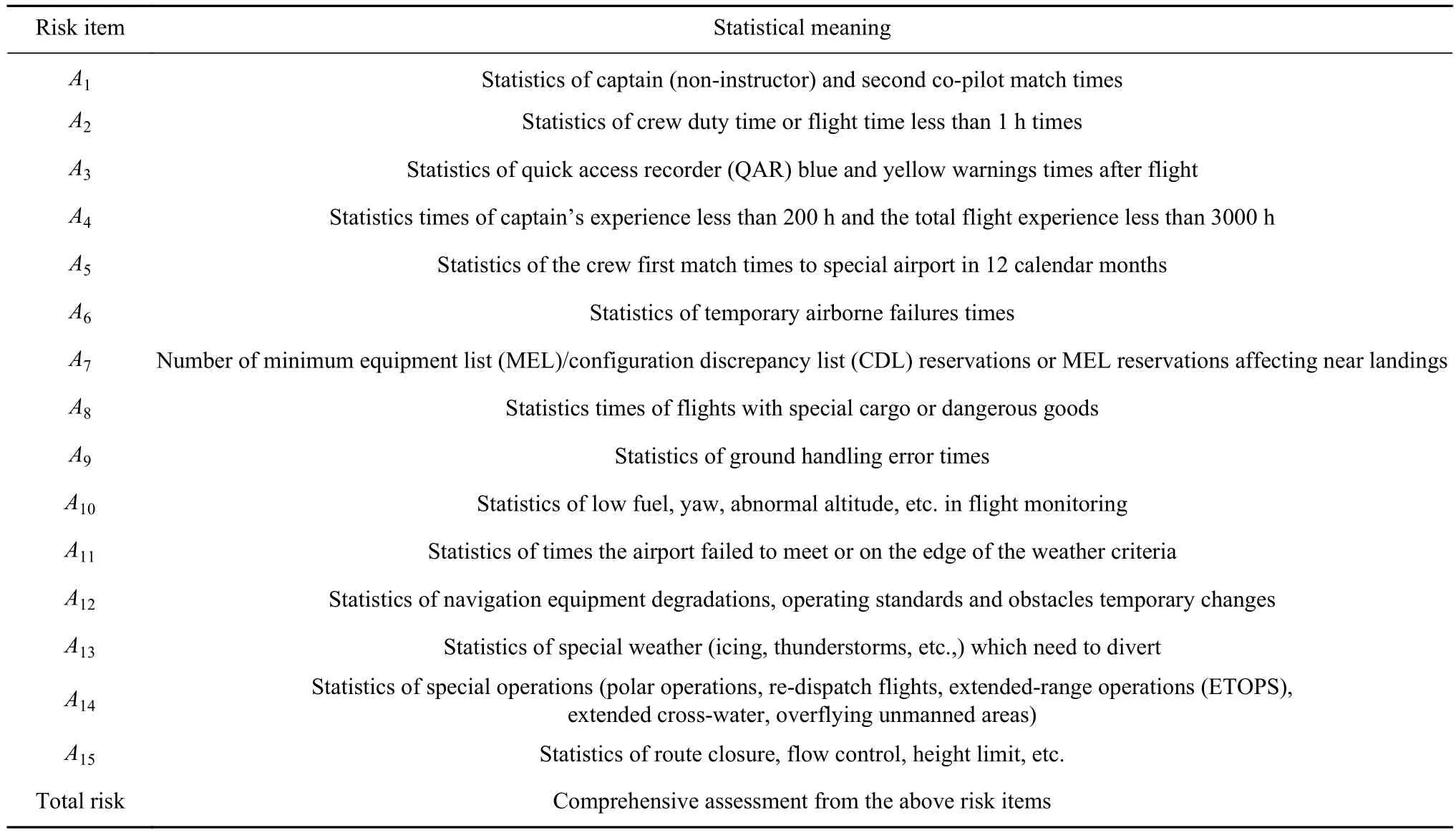
表2 航班运行风险统计数据Table 2 Risk assessment statistical data
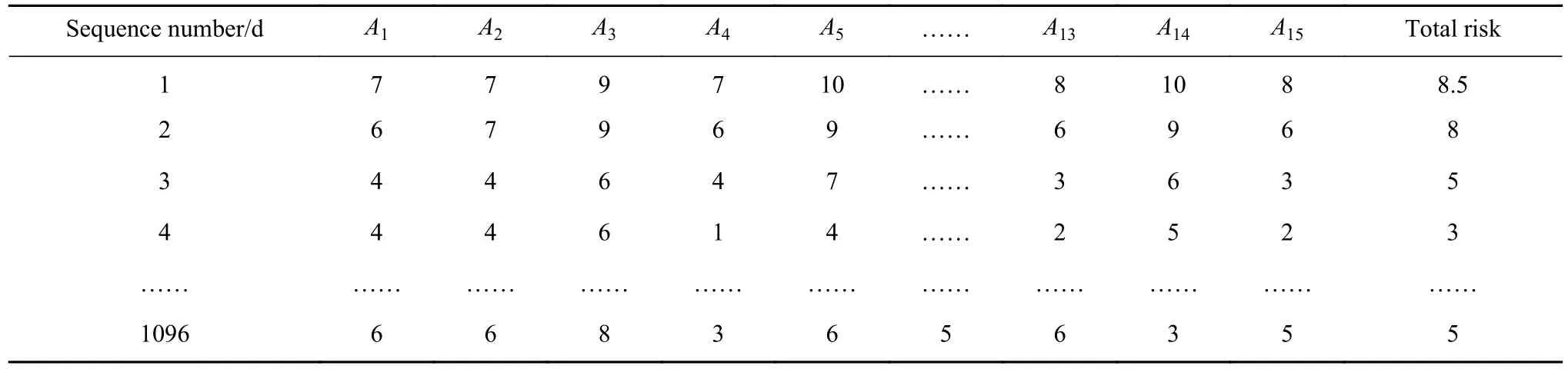
表3 航班运行风险时间序列局部数据样本Table 3 Time series sample data of flight operation risk
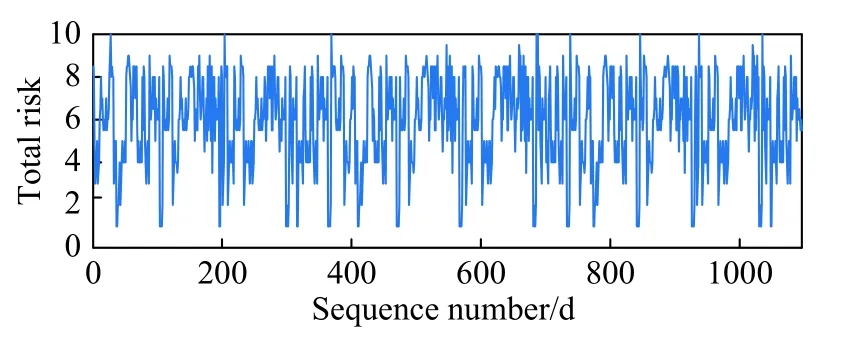
图1 航班运行总风险时间序列Fig.1 Time series example of flight operation total risk
2 多变量混沌预测模型构建
2.1 多变量时间序列相空间重构
多变量时间序列相空间重构由单变量相空间重构发展而成.以15个风险序列的多变量相空间重构结果作为预测模型的输入,可使模型输入包含各个风险序列的历史信息.
对于长度为N的n个时间序列,j=1,2,···,n,时间延迟为τj和嵌入维为mj,运用坐标延迟重构法如式(1),则多变量时间序列重构后的相空间如式(2):
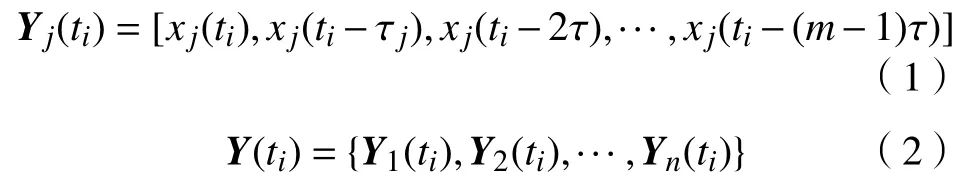
式中,ti=max{(mj-1)*τj}+1,···,N-1,N.
τj和mj选择是相空间重构的关键.根据Takens定理,设d为混沌吸引子的维数,若m≥2d+1,则可在m维空间中重构出与风险序列混沌吸引子保持微分同胚的轨线[23].采用C-C方法计算风险序列的最佳τj和mj.以风险时间序列Xj(t)为例,计算过程如下:
(1)设N是风险序列数据的个数,σ是标准差,并定义为:
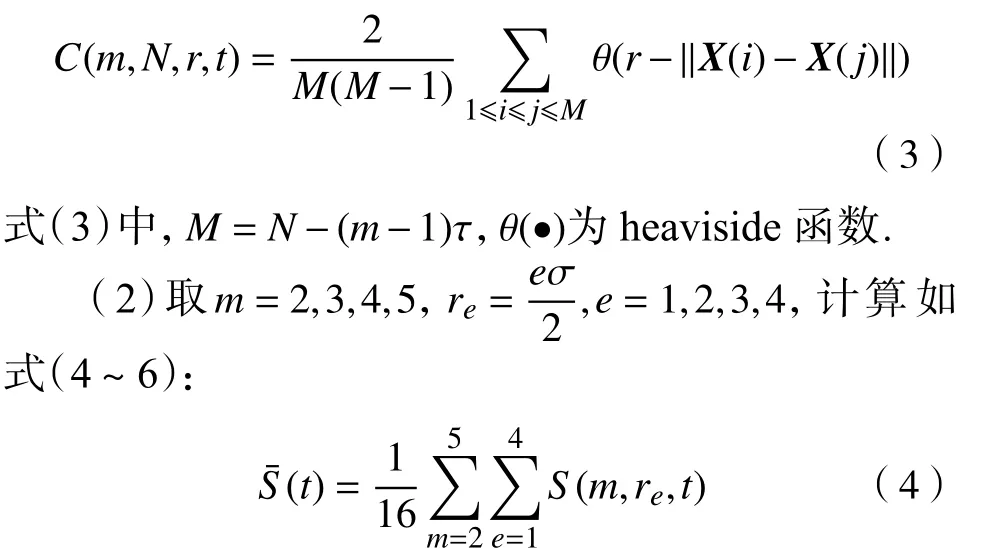
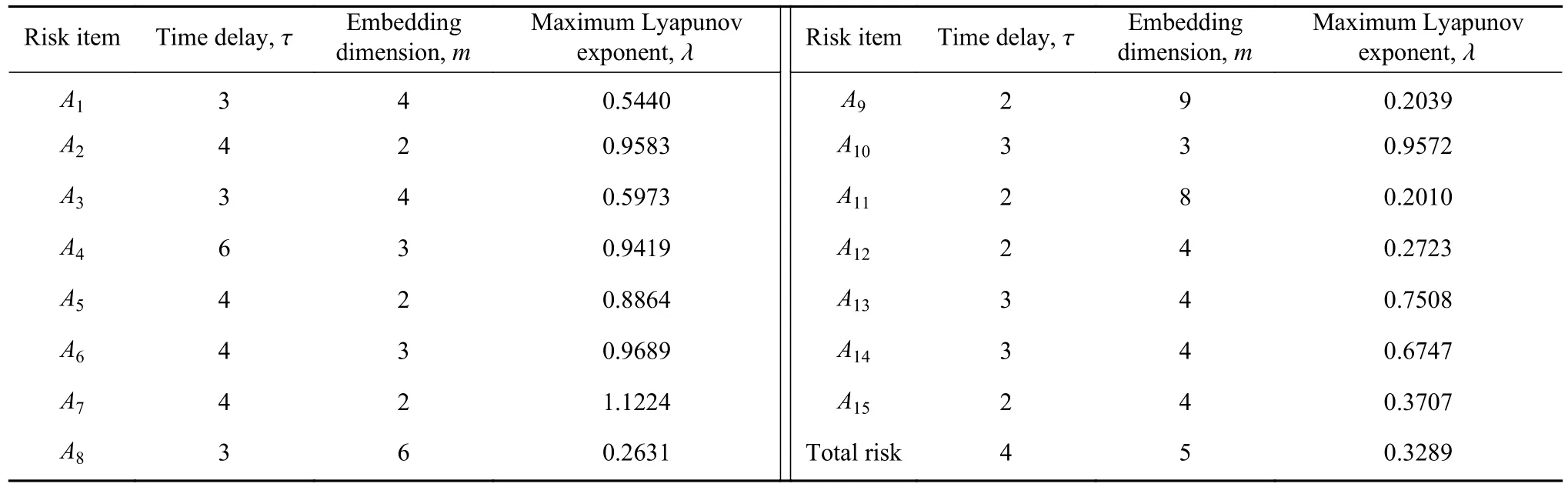
表4 时间序列的时间延迟、嵌入维和最大Lyapunov指数Table 4 Time delay, embedding dimension, and maximum Lyapunov exponent of the time series
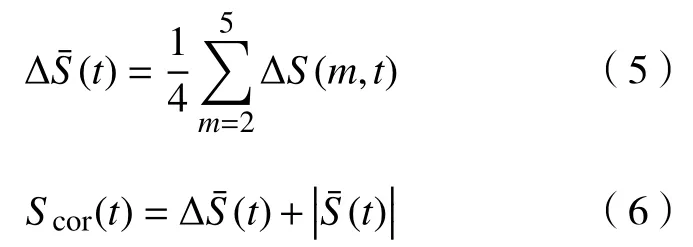
式中,S(m,re,t)=C(m,re,t)-Cm(1,re,t),ΔS(m,t)=max{S(m,re,t)-min{S(m,re,t)}.
τj和mj的合理选择有助于对混沌系统的拟合和预测,表4为15个风险时间序列的最佳延迟时间和嵌入维,据此可进行多变量时间序列相空间重构,重构后的维度为各个序列的总嵌入维
2.2 基于 PCA的相空间降维方法
由于航班运行风险各指标变量均代表不同含义、混沌重构过程的τj和mj也不尽相同,所以在多变量相空间重构后,不同变量在不同历史时期的观测数据混合在一起,可能造成了信息冗余或噪声干扰,产生预测误差.采用PCA抑制此问题.PCA基本思想是将一组具有一定相关性的变量重组为互不相关的主成分,通过保留方差贡献率较大的主成分代替原变量,实现数据降维.采用PCA改进航班运行风险的预测过程,可以保证:①预测模型的不同输入成分之间相互独立、信息不重叠;②输入的状态空间在保证尽量多信息的情况下实现维度降低.
PCA常用的主成分提取方法有特征值分解(Eigen value decomposition, EVD)和奇异值分解(SVD),相对于EVD,SVD在数据重构上误差较小,故本文采用基于SVD的PCA进行降维处理,设ξ1≥ ξ2≥ ···≥ ξq> 0为原相空间Y的奇异值,通过SVD进行分解如式(7):

式中,Q=[q1,q2,···,qN-τw]为Y的左 奇异矩阵,为Y的右奇异矩阵,D=diag(ξ1,ξ2,···,ξd).
假设前 γ个主成分的累计方差贡献率为Gγ,见式(8),一般认为,当满足Gγ≥85%时[24],可将γ个主成分构成的状态空间,见式(9),代替原相空间,实现降维.

2.3 预测模型
混沌时间序列预测理论中常用方法有:全域法、局域法、基于Lyapunov指数预测法、基于Volterra自适应滤波器预测法、基于神经网络预测法等.此处在选取方法时,一方面总结以往研究,发现神经网络类方法在混沌预测中表现较为突出;另一方面,通过查阅文献,筛选出预测结果最好的几种方法,包含了极限学习机[18]、RBF神经网络[25]、回声状态网络[26]和Elman神经网络[21]等.而后,通过原理分析发现,上述4个模型均由传统神经网络发展而来.两方面相互印证,决定采用该4种方法,后续分别构建短期预测模型,通过误差分析,提出具有较好适应性的预测方案.
对于给定的N个不同样本{(u(i),O(i)),i=1,2,···N},其中u(i)=[u1(i),u2(i),···,ul(i)]T∈Rl为输入层,O(i)=[O1(i),O2(i),···,Ov(i)]T∈Rv为输出层.统一设定隐含层神经元个数为h,隐含层神经元与输入层的连接权值为、与输出层的连接权值为,其中j=1,2,···,h.不同模型的原理如下:
(1)极限学习机ELM.
ELM是单隐层前馈神经网络,如图2.设ELM隐含层神经元的阈值为b,训练过程中,win和b随机产生,并保持不变,加快了神经网络的训练速度并使之具有较好的泛化能力.
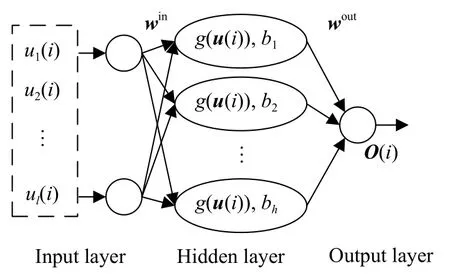
图2 极限学习机结构Fig.2 ELM structure
图2中,从输入到输出的函数表达式为:
式中,i=1,2,···N;只需设定隐含层神经元个数h,并确定激活函数,并通过求解式(11)即可得出wout,其中,激活函数多选用sigmoid函数.

式中,H†为H的伪逆,H为隐含层输出矩阵,即
(2)RBF 神经网络.
RBF是从三层前向型网络发展而来,不同之处在于其隐含层的神经元变换函数使用径向基函数.RBF神经网络的优点在于输入层和隐含层之间不需通过权值连接,当RBF中心点确定以后,即可确定二者的映射关系,从而使网络结构简单、训练简洁.
图3中,{Rj,j=1,2,···,h}为激活函数,常使用高斯函数如式(12),由此,从输入到输出的函数表达式为:
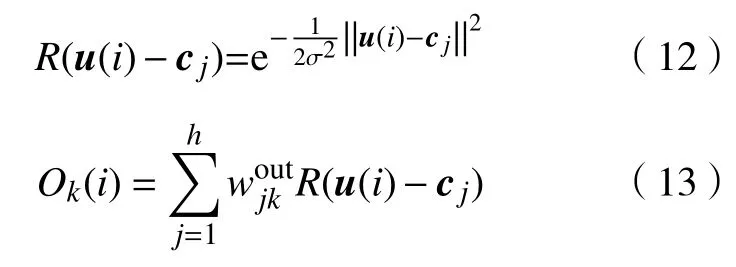
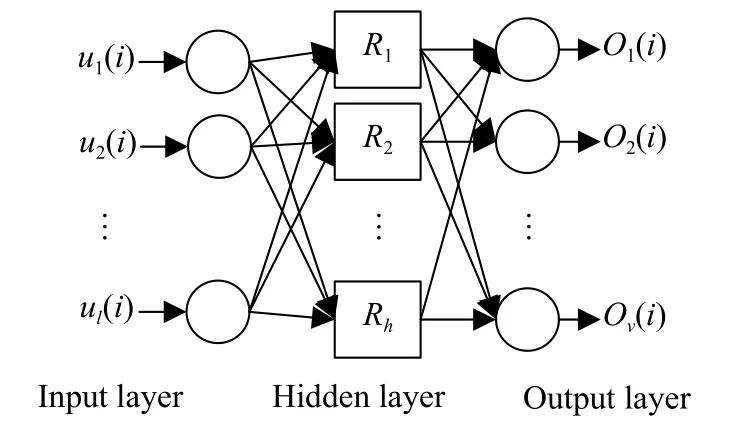
图3 RBF神经网络结构图Fig.3 RBF neural network structure
(3)回声状态网络.
回声状态网络(ESN)是一种递归神经网络,结构如图4,与传统神经网络相比,ESN使用大规模随机连接的递归网络形成一个储备池,取代隐含层,通过预先设定储备池权值矩阵的谱半径可保证网络的稳定性.
ESN从输入到输出的表达式为:
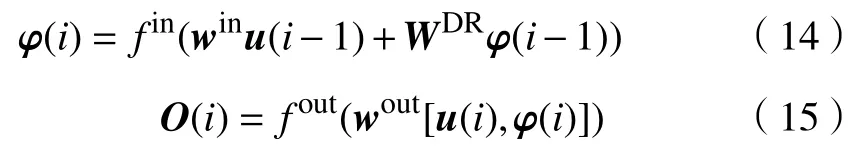
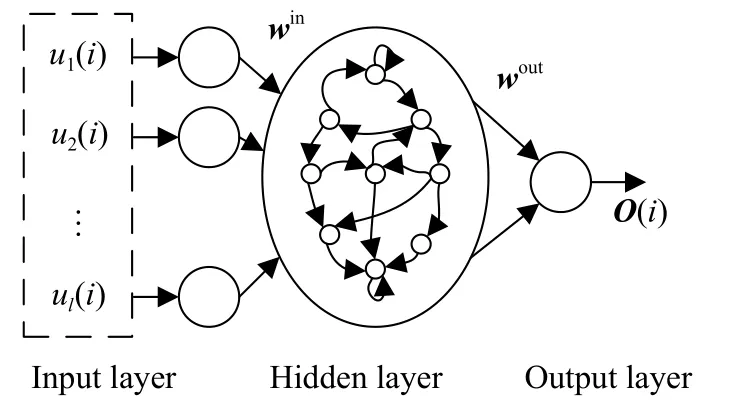
图4 回声状态网络结构图Fig.4 ESN structure
式中,φ(i)为储备池的状态向量,WDR为储备池内部连接权值矩阵;fin为激活函数,常取双曲正切函数;fout为输出函数,常取恒等函数,此时wout可通过下式求解:

式 中,B†为B={u(β+1),u(β+2),···,u(N)}的伪 逆,{u(1),u(2),···,u(β)}为舍弃的一段初始数据.
(4)Elman神经网络.
Elman是一种典型的局部回归网络,属于反馈神经网络,如图5,它与前向神经网络不同之处在于隐含层中增加了一个承接层,构成局部的反馈.承接层用于接受隐含层前一时刻的输出信号,并作为下一时刻输入信号的一部分重新输入到隐含层中,形成一个一步延时算子,使网络具有动态记忆功能.由于承接层具有可以记忆过去状态的特性,非常适合时间序列预测问题.
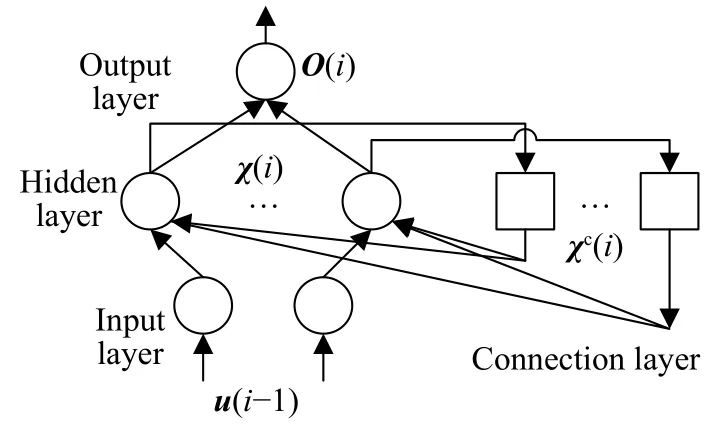
图5 Elman神经网络结构图Fig.5 Elman neural network structure
Elman从输入到输出的表达式为:
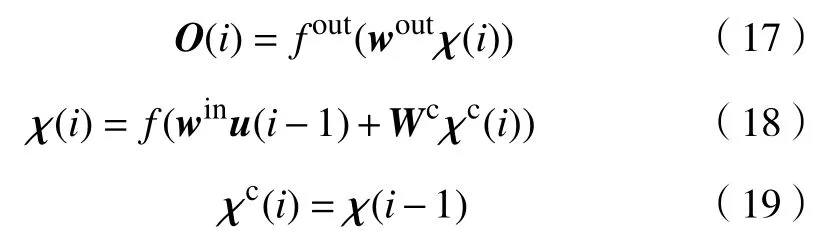
式中,χ(i)为隐含层神经元向量,χc(i)为承接层的反馈向量,Wc为承接层到隐含层的连接权值,f为隐含层神经元的传递函数,fout为输出函数.
2.4 预测流程
根据A1~A15风险时间序列,对未来pd的总风险值进行短期预测,预测流程如图6:
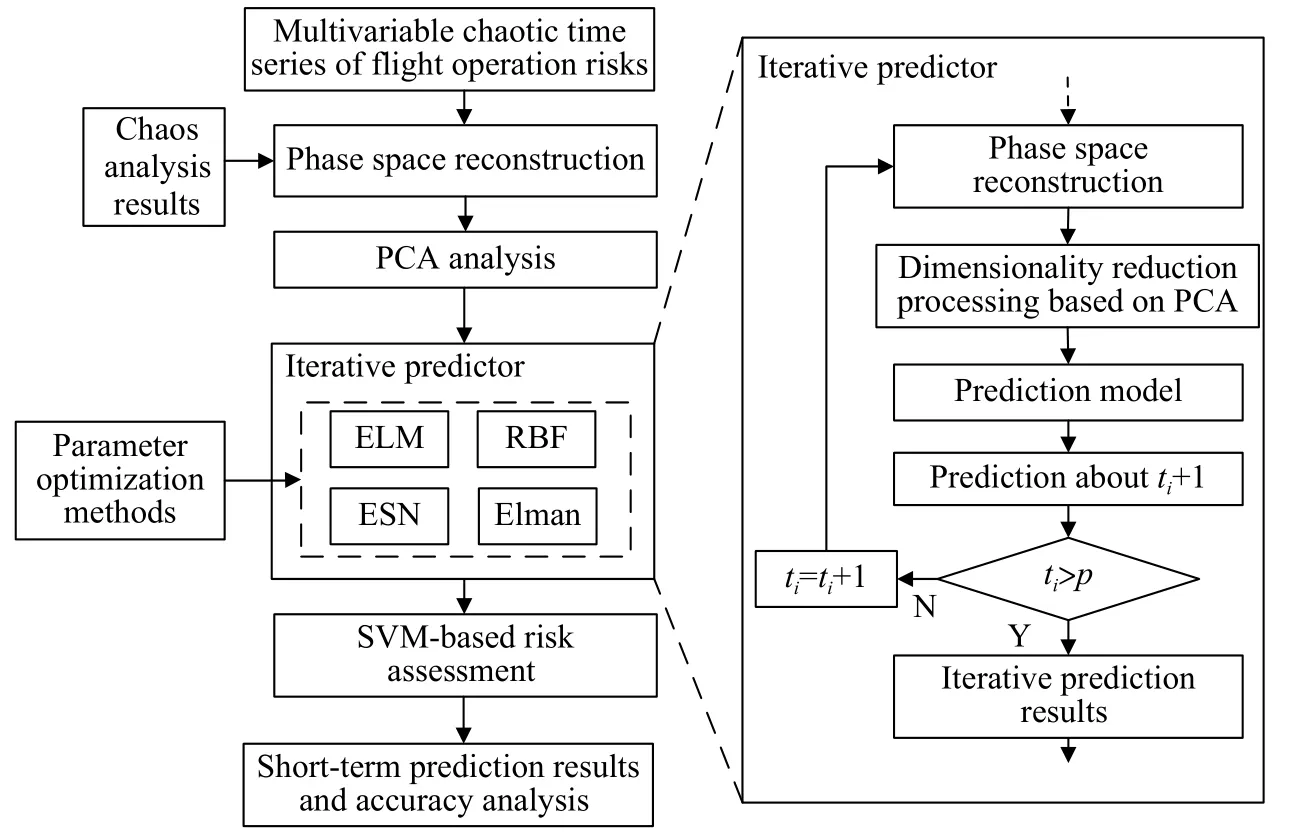
图6 预测流程Fig.6 Prediction process
1)根据风险项A1~A15的混沌特征分析结果,确定延迟时间和嵌入维,进行多变量相空间重构;
2)对相空间进行PCA分析,确定前若干个主成分构成的状态空间,实现相空间的降维;
3)根据迭代预测方法,分别构建ELM、RBF、ESN和Elman风险短期预测.假设当前时刻为ti,在迭代预测过程,首先以第ti天降维后的状态空间作为预测模型的输入,预测出第ti+1天A1~A15的风险值;然后,利用第ti+1天的预测值,重新进行多变量相空间重构并作降维处理,再将此时降维后的状态空间输入至预测模型中,预测出第ti+2天A1~A15的风险值.以此类推,直至完成第ti+p天的预测,得到A1~A15的pd预测结果.
4)采用支持向量机(SVM)进行风险评估,得到总风险值的pd预测值,通过与总风险的真实值比较,计算预测误差并分析不同模型的预测精度.
3 实例分析
3.1 主成分降维
将15个风险源时间序列数据作为预测样本,其中,将前900 d作为训练集,剩余196 d作为测试集.经过多变量相空间重构后再使用PCA降维,各主成分的方差贡献率如表5.
根据PCA原理,PCA处理后得到的主成分应能解释原始变量尽量多的信息,累计方差贡献率达到85%以上为宜;同时,当变量之间相关性较强的时候,少数几个主成分的累积贡献率就能达到较高水平,当变量之间相关性较弱的时候,则需较多的主成分才能达到较高的累积贡献率,但更为重要的是保证计算后达到有效的降维效果.因此,在较高的累计方差贡献率基础上结合碎石图拐点出现位置,再综合选择.通过采用85%、90%和95%不同阈值,经上文预测流程计算得到,当保留前31个主成分累计方差贡献率为90%时,此处预测结果最为理想,即维数由62维压缩至31维.
3.2 参数优化
根据训练集数据,采用交叉验证法、遗传算法和粒子群算法对预测模型的参数进行优化.但由于后续预测过程采用多步迭代方式,过程复杂且易受预测步长的影响,因此假设多步迭代预测最优的前提为单步预测结果最优,综合衡量不同参数优化方法和多次试验的输出,参数优化结果如表6所示.
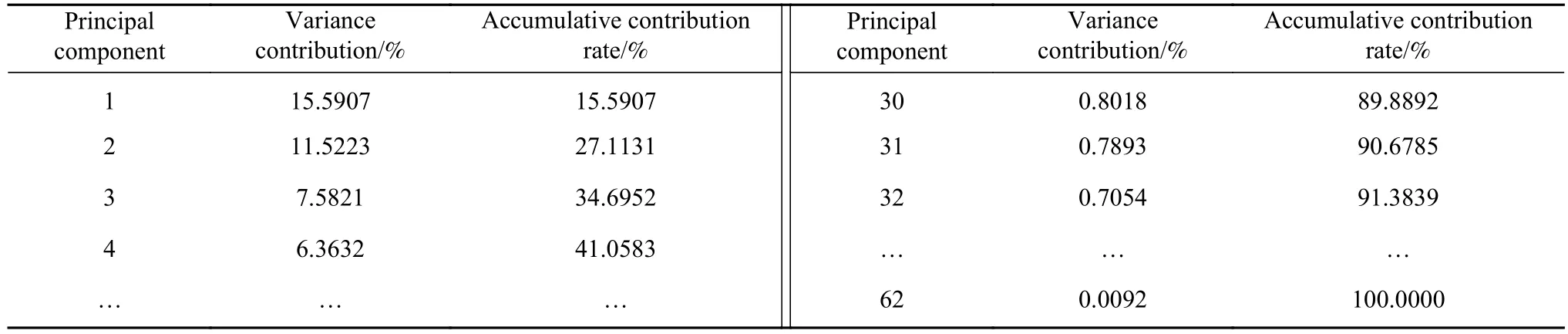
表5 主成分分析的方差贡献率Table 5 Partial variance contribution rate of PCA
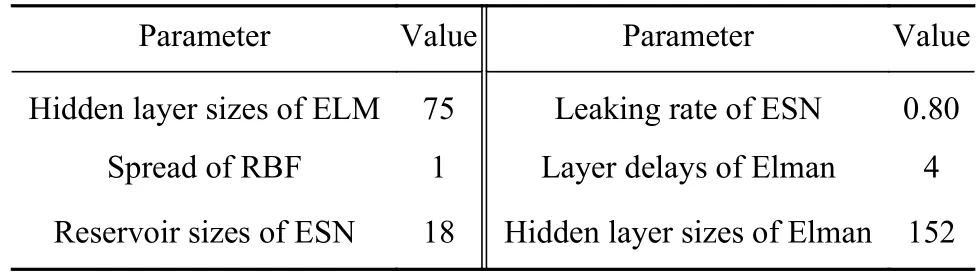
表6 预测模型的参数优化结果Table 6 Parameter optimization results of the prediction models
3.3 短期预测的测试结果
结合航空公司实际需要,设定预测范围为未来7 d,以第900天为起始点,向后预测得到第901~907天风险值,如图7.但仅从一组数据无法说明模型预测精度,再从第901天至第1090天依次预测,总计190次,每次均得到7 d预测结果.统计所有预测的第1、3、5天结果如图8;其中,图8(a)均为第 1 天预测结果,其范围为 [901,1090];图8(b)是第 3 天结果,范围为 [903,1092];图8(c)是第 5 天结果,范围为 [905,1094],图8(a)(b)(c)均包含190个数据.
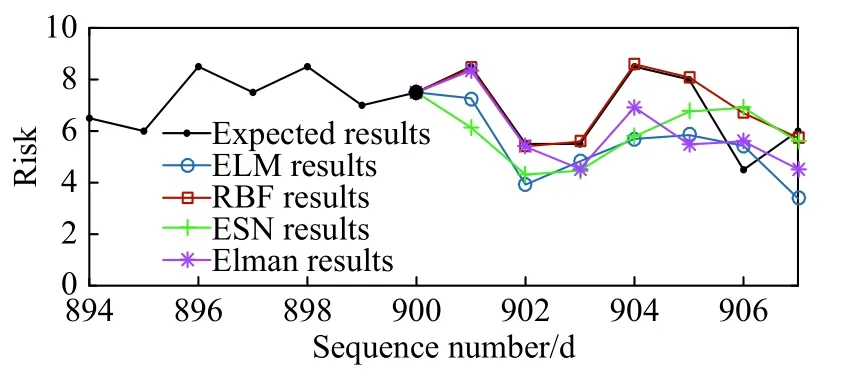
图7 从第900天向后预测样例Fig.7 Example of prediction results from the 900th day
3.4 结果分析
计算ELM、RBF、ESN和Elman等不同模型短期预测结果的相对误差.统计相对误差(Relative error, RE)的频数分布,并以降维前的预测作对比,如表7.
从表8可见,RBF降维后的预测效果最佳,对于RE<25%的预测结果,未来第1天占比达到82.62%,第3天为78.95%,第5天仍高于75%,随预测范围的增加,预测精度逐步递减.4种预测模型在降维后,第1天预测结果RE<50%的出现频数平均为90.65%,第3天为 86.18%,第5天为 85.26%,表明RE>50%的异常结果出现次数较少,4种预测模型均可行有效.进一步对比降维前后结果发现,降维后RE<50%占比相对于降维前提高了约6%,说明降维处理有助于提高RBF的预测精度.
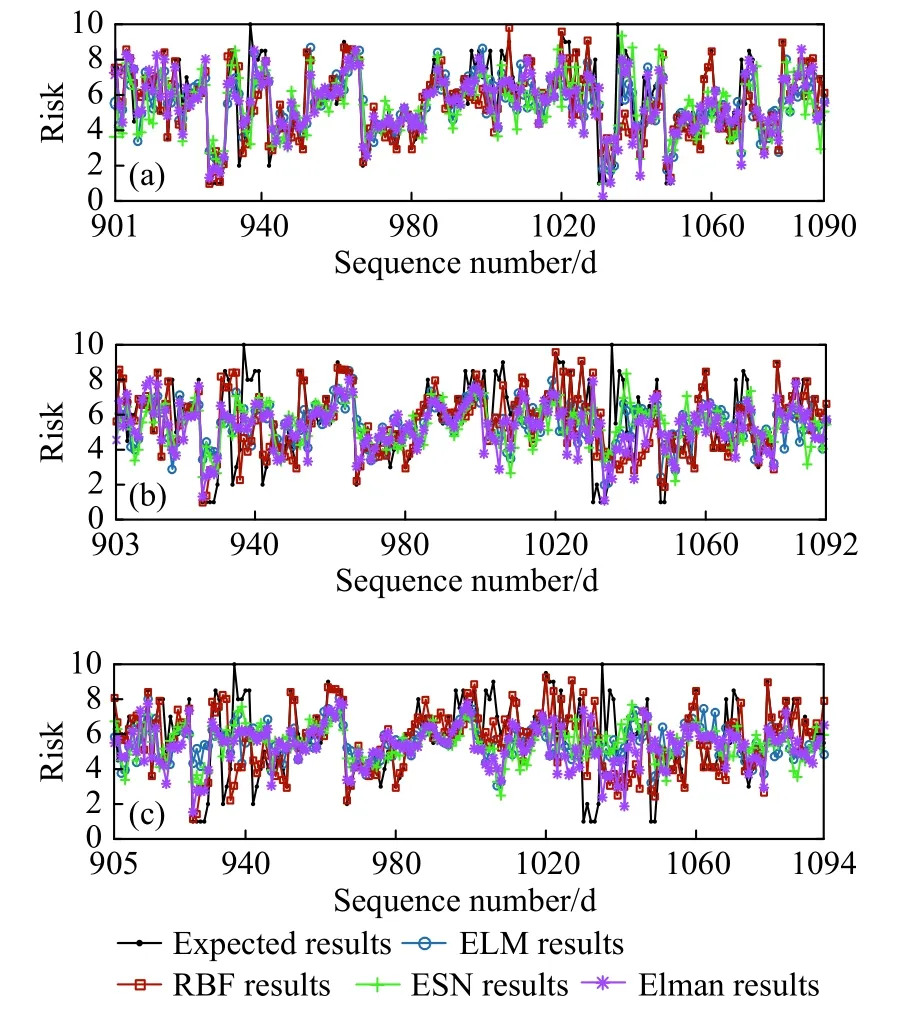
图8 预测结果示例.(a)第 1 天;(b)第 3 天;(c)第 5 天Fig.8 Example of prediction results: (a) day 1; (b) day 3; (c) day 5
3.5 误差分析
从表7可见,不同模型预测相对误差的频数分布均呈右偏,若以均值反映相对误差的集中趋势,结果会偏大.因此,为使相对误差均值(MAPE)更具代表性,采用修正的MAPE值,即去掉最大5%和最小5%的数据后所求得的MAPE值,结果见图9~10.
从图9可见,当训练样本为300时,误差较大;随着训练样本增加,误差开始下降;当训练样本从300增加至500时,7 d内的修正MAPE值平均下降5.48%,预测效果明显提升;当训练样本从700增加至900时,修正MAPE值平均下降1.27%,效果提升开始放缓;当训练样本从800增加至900时,修正MAPE值平均仅下降0.21%,可视为无明显变化;因此,基于现有数据情况,后续使用训练样本为900进行计算.
图10是基于降维后的RBF预测结果,修正MAPE值随预测周期增长而逐步递增,从第1天至第7天平均每天增加2.35%,呈现误差累积现象.第1天修正MAPE值仅为11.32%,精度较高;第5天MAPE值仍为18.21%,其预测精度和预测周期均优于文献[12]和[13].根据国内航空公司使用要求,当预测相对误差低于20%时,结果具有实践操作价值,因此该方法所得未来5 d预测结果均可作为依据进而指导生产实践.
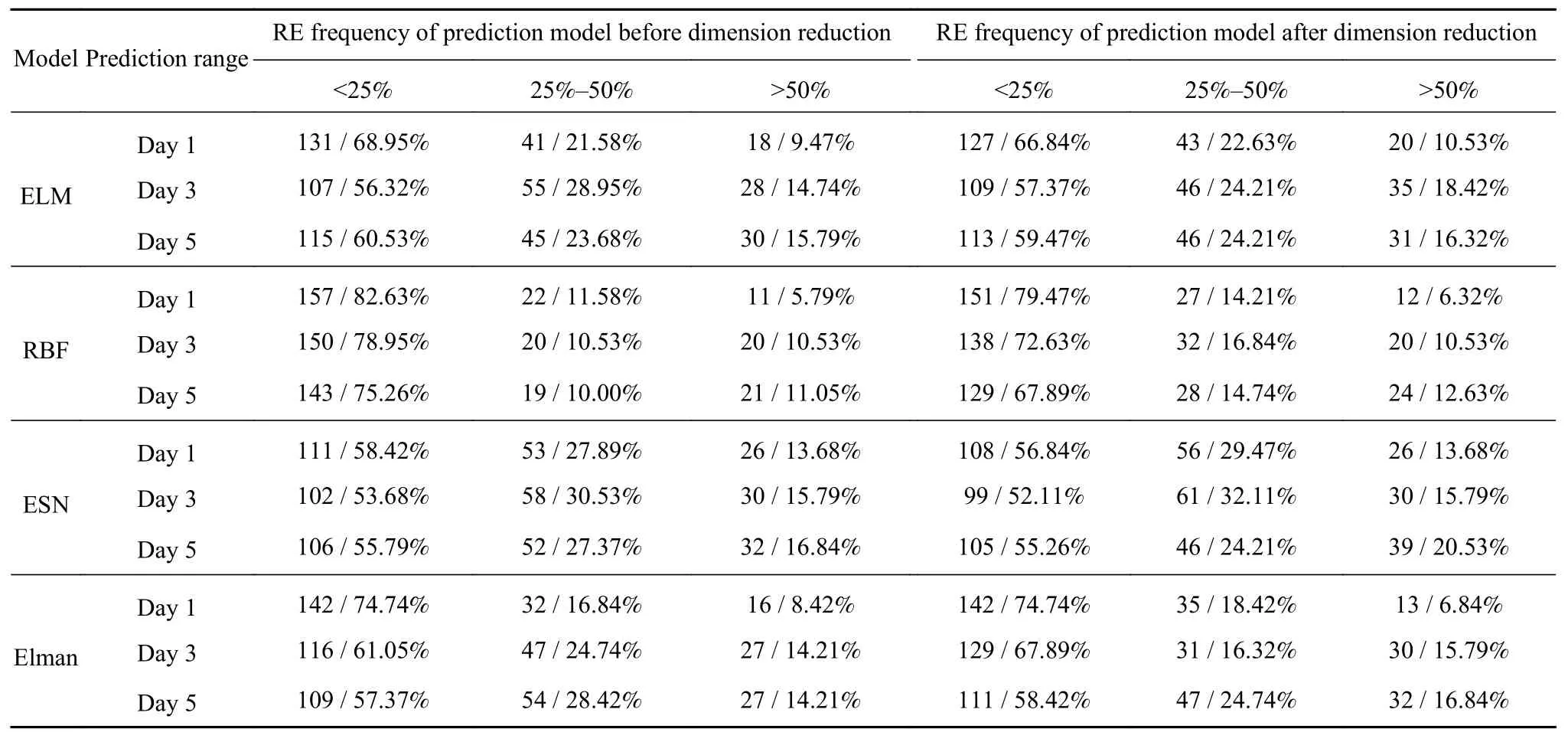
表7 各模型降维前后预测相对误差频数Table 7 RE frequency of each prediction model before and after dimension reduction
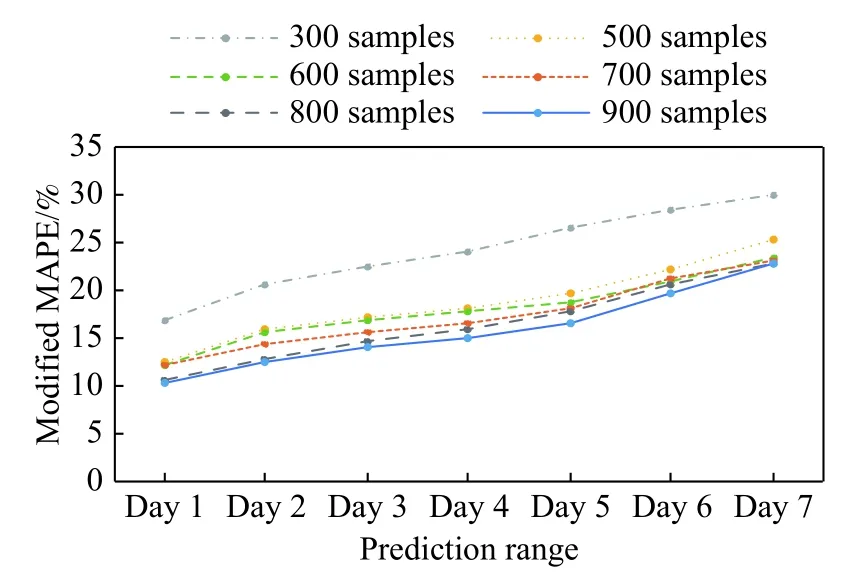
图9 训练样本数量与预测精度Fig.9 Number of training samples and prediction accuracy
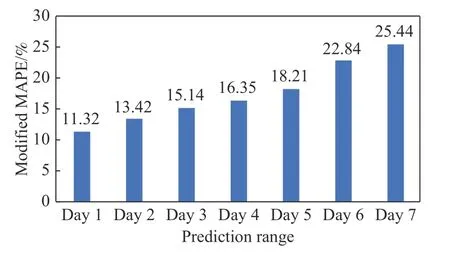
图10 RBF降维后的多变量预测精度Fig.10 Prediction accuracy of the RBF model after dimension reduction
4 结论
通过混沌识别和相空间重构,构建的4种风险预测模型在迭代预测后发现:在降维前后的ELM、RBF、ESN和Elman预测模型中,降维后的RBF预测模型效果最佳;其未来第1天预测结果RE<25%的频数可达到82.62%,修正MAPE值仅为11.32%;至第5天MAPE值仍为18.21%,说明未来5 d的预测结果均可满足航空公司实践操作要求.从预测精度和周期两个角度综合评判,多变量时间序列方法对航班运行风险的预测可行且有效.
国内航空公司以周为单位制定航班计划,因此可在文中结果基础上,最早于5 d前从飞机调配和人员调度等方面调整计划编排,提前降低运行风险.该方案还可扩展至其他领域,适用于结果受多变量综合影响的、各变量为混沌时间序列的短期预测问题,其预测周期随多变量的混沌时间序列特性而定.
