卷积神经网络在矿区预测中的研究与应用
2021-01-04袁传新贾东宁周生辉
袁传新,贾东宁✉,周生辉
1) 中国海洋大学信息科学与工程学院,青岛 266000 2) 青岛海洋科学与技术试点国家实验室高性能科学计算与系统仿真平台,青岛266000
富钴结壳是继大洋多金属结核之后发现的又一深海固体矿产资源,堆积在海底岩石和岩屑表面,主要由氢氧化物和铁锰氧化物组成.结壳除了钴元素外,还富含稀土元素和其他的许多金属,例如铁、镁、镍、铜、锌等,具有非常高的开采价值[1].富钴结壳的形成和其他矿产资源一样,是非常缓慢的自然生成过程,每100万年只能产生1至6 mm的结壳.矿床主要分布于碳酸盐补偿深度(CCD)以上、最低含氧层以下水深 500~3500 m的平顶海山、海台顶部和斜坡的表面[2-4].海洋里有诸多海山,仅仅在太平洋区域广义海山有约50000多座,高度大于1000 m的海山就有约8000多座[5].富钴结壳矿床有非常高的经济价值,估计潜在资源量达10亿吨[6].富钴结壳是海洋中典型的水成成因的矿产资源,由于形成于古海洋和古沉积环境,除了资源本身的经济价值,富钴结壳还记录了海洋和气候的演化历史,具有非常高的环境研究价值[7].正是由于具有巨大的经济价值和环境价值,钴结壳资源一直是海洋调查的重点.我国富钴结壳资源的调查开展的比较晚,90年代末才系统的开展起来,投入巨资开展了若干综合航次调查,至今20多年的时间也仅仅调查了几十座海山.1997~2002年的航次主要是选择靶区的侦察性调查,使用多波束、浅剖、重磁、海底摄像和温盐探仪(CTD)等的环境勘测和使用抓斗、拖网等的地质取样调查.2002年以后的航次对部分调查过的海山进行加密采样,调查方法增加了可视抓斗、可视浅剖等[7].无论是初始侦察点的选择还是之后对整个矿区的圈定,都需要对大范围的诸多海域进行大规模的海山结壳资源调查.科考船需要对未知的区域进行随机靶点调查,且对于确定的结壳矿区的边界的界定还需要进行大量的勘察工作,这些都将耗费大量的人力、物力和时间.
科考船对不同海域多年的普查工作积累了大量的宝贵资料和数据,并且这些数据正在以指数级的形式增长.如何把这些数据合理的运用起来,促进海洋地质的研究进展,成为了科研工作者关注的热点问题.作为大数据分析和处理的重要技术手段,机器学习方法在找矿领域也得到了广泛应用.研究发现,地形是结壳富集的一个重要因素,富钴结壳富集区具有坡度、平整度等明显的地形特征.随着遥感等技术的进步,海拔高度的获取更加精确,利用密集采点的海拔高度矩阵作为区域地形特征,具有较高的区分度.机器学习的分支深度学习善于处理多维数据错综复杂的关系,运用大量的输入和输出得出映射关系[8].其中卷积神经网络从复杂数据中提取特征表现突出,在诸多领域被广泛应用,特别是图像分类领域取得了非常好的效果[9].卷积神经网络结构与数值矩阵能够更好吻合,自动完成特征提取,其权重共享机制可以降低网络复杂性,适合本文基于数值矩阵的地形特征区分类找矿任务.
本文从结壳矿区的地形特征出发,利用卷积神经网络对大量的数值矩阵训练学习得到预测模型,对矿区靶点进行预测.另外,对本文方法的应用及后序研究工作进行了展望.
1 研究现状
自1959年国内就开始出现了找矿靶区的相关研究,随着研究的深入,出现越来越多与“找矿靶区”相关的关键词[10].找矿使用的方法一般有经验类比法、综合信息法和数学模型法等,逐渐从经验找矿向理论和科学找矿过渡.如,刘泉清等提出利用经验法和化学普查相结合的方法[11],杨恒书等创用浓度级次值特征对比模型和相近率线性模型[12],中国科学院地质与地球物理研究所总结提出“三场异常互相约束”预测新理论[13],张庆华等提出物探、化探与遥感相结合的方法[14].随着科学技术的发展与研究的不断深入,诸多新技术、新方法被应用到找矿中来.智能找矿方法是在地质类比法和模型法应用的基础上,结合计算机技术,将已有的专家经验和一定的矿床模型输入计算机,建立起预测模型系统,将研究区的有关资料输入,在此基础上进行评判.如,王世称主导的综合信息矿产预测系统[15],赵鹏大的大比例尺矿床统计预测专家系统[16]等.深度学习和机器学习迅猛发展,硬件技术的进步,简洁的python语言、完善的深度学习框架Tensorflow以及基于Theano/Tensorflow更简单易上手的高阶框架Keras,推动了智能找矿发展.已有许多学者投入到机器学习与找矿以及成矿预测的研究中来,如徐述腾和周永章以吉林夹皮沟金矿和河北石湖金矿的黄铁矿、黄铜矿等为例,设计了Unet卷积神经网络模型,实现了镜下矿石矿物识别分类[17];刘艳鹏等通过卷积神经网络算法挖掘Pb分布特征与矿体地下就位空间的耦合相关性进行矿产资源预测[18],肖壮等提出基于深度学习的矿区韧性剪切带找矿研究[19]等.然而,大部分研究是以陆地矿为基础的,海洋底部矿区的找矿工作要复杂许多,迫切需要在找矿靶区的选取方面进行改进,增加成功找到矿区的可能性,减少时间和人力、物力成本.
2 地形特征与理论方法
2.1 海山富钴结壳矿区地形特征
结壳的形成及其丰度变化受控于诸多因素,经纬度、区域地质构造、水深、地形和水文等都会对结壳的生长产生重要影响[20].例如,海山经纬度位置决定了海山洋流速度以及流向,进而决定了结壳的附着程度、丰度以及类型;大量的研究成果以及统计数据表明,水深影响结壳的生长和富集,结壳大部分分布在水深1000~3000 m范围内;结壳的产生来源于海水中的微生物和钙质粒子,水文环境也是一个重要因素.研究认为,结壳分布与海山的地形特征具有一定的关系,控制作用效果也比较明显[21].结壳产生于各大洋区的水下高地,海山和岛屿斜坡是主要富集区,海山对结壳成矿具有重要意义.三大洋中,太平洋海山富钴结壳矿点的分布比例占到了73.3%.在空间上,海山山顶区一般为微结核发育区,在海山的局部高地会有结壳生长成矿[22].海山分为尖顶海山和平顶海山两大类,尖顶海山山顶、边缘、上部斜坡及中部斜坡区山脊部位最容易成矿,平顶海山边缘和除陡崖外的上部斜坡区成矿率也较高[23].
图1表征了本文数值矩阵反应的地形特征,横纵坐标表示各海拔取值点相对于第一个点的水平方向距离d1和d2,竖坐标轴表示各取点海拔高度h,均以米为单位.从形态学上讲,海山的形态要素主要包括海山坡度、海山表面平整度[24],因此要考虑的因素主要有坡度和海山微地貌特征.地形坡度太小,海水中的物质不容易沉积;在地形坡度较大的地方,结壳生长过程中容易塌落[25].坡度较大和坡度较小都不利于结壳的形成.根据矿物质沉积理论,颗粒最容易在凸起的部分聚集,山坡上的裸露岩石成为结壳生长有利位置.对本文获得的数值矩阵计算坡度值得表1,坡度大部分处在8°~12°范围内,坡度较陡的地形较少.
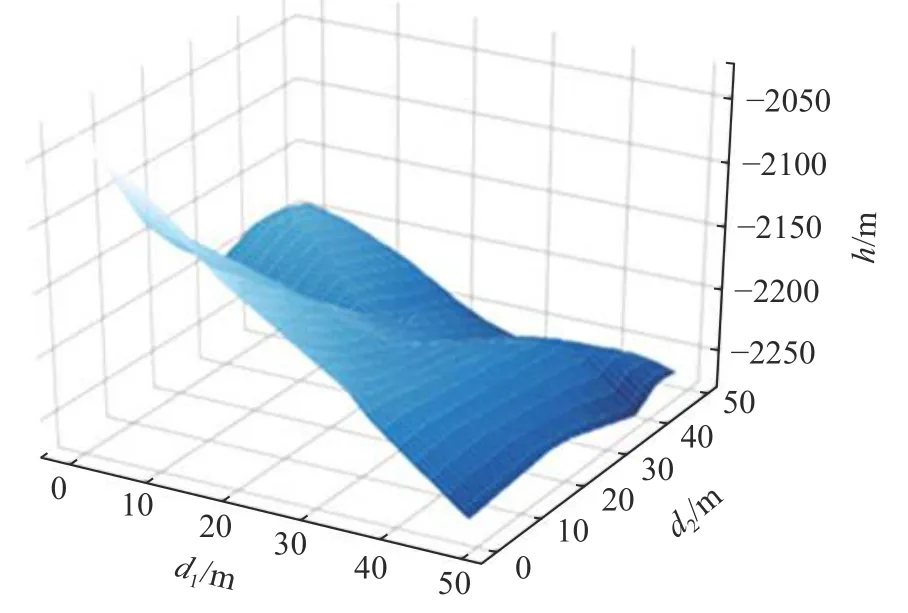
图1 局部海山地形Fig.1 Local seamount terrain

表1 地形坡度统计Table 1 Topographic slope statistics
分析认为,富钴结壳在一定范围内的坡度和平整度的海山区域容易生长富集,具备明显的分类特征,可以作为找矿靶点的依据.运用容易获得的海拔高度矩阵作为地形特征,并采集大量的正负样本,使用在分类问题上表现优异的卷积神经网络进行二分类,进而成为富钴结壳矿区和结壳富集海山选定的参考依据,具有现实意义.
2.2 数据处理方法
2.2.1 数据标准化
数据标准化(归一化)的目标是突出主要特征的作用,弱化次要特征的影响.富钴结壳在不同海拔高度位置均有站点,地形矩阵数值分布在-4000~-800 m之间,跟前文提及富钴结壳主要分布在1000~3000 m范围内基本一致.不同的矩阵数值的平均高度差别很大,而需要考虑的主要因素是整个矩阵反应的地形特征,高度数值的大小属于次要因素,因此要处理高度之间的差别.
常用的两种数据标准化的方法是min-max和Z-cores.min-max标准化对原始数据进行变换,把结果值范围映射到0~1之间,函数为(1),min和max分别为最小值和最大值.Z-cores标准化处理数据使之符合标准正态分布,函数为公式(2),μ和σ分别为样本均值和方差.本文对min-max标准化方法做了改变,首先计算所有矩阵的max与min之差,取差值的最大值MAX,然后将公式(1)中分母部分替换为MAX,函数为公式(3),目的在于防止崎岖地形与平缓地形混淆.
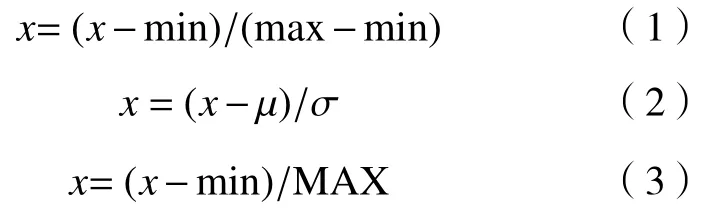
2.2.2 插值算法
双线性插值算法根据插值点最接近的4个点的像素值进行计算.设(i+u,j+v)为坐标变换后浮点坐标,f(i,j)为坐标(i,j)位置的像素值,f(i+u,j+v)即为坐标变换后的像素值,其中i、j为整数部分,u、v为小数部分[25].则这个像素值可由公式(4)得出.该算法保证了插值曲线的平滑性,弥补了最近邻算法的不足,是插值效果和运算速度相对较优的算法,也是使用最广泛的.
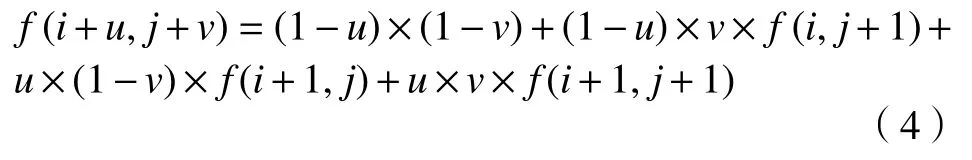
2.3 模型结构
本文的数值矩阵代表的是矿区地形,每一个数值都有空间位置关系,相当于图像中的像素点.因此,与特征提取和支持向量机(SVM)、随机森林等传统统计方法结合相比,使用更适合图像处理的卷积神经网络.卷积神经网络与传统深层神经网络相比,可以明显降低模型规模,并且识别性能最好,泛化能力最强[26].
针对数据集特性,搭建了适合本文区分类找矿研究的Conv-3模型.图2给出了Conv-3模型的结构图,该卷积神经网络网络共包含7层:一个输入层,三个卷积层C1、C2和C3,两个全连接层F4和F5,一个输出层.在该模型中,输入层的输入为50×50的数值矩阵,卷积层均使用16个5×5的卷积核,全连接层分别使用2048和128个神经元,输出层使用softmax函数进行分类.
VGGNet16是一种深度卷积神经网络结构,通过不断深化网络结构提高性能[27],在此结构中卷积层均使用3×3的卷积核,池化层使用的是Maxpooling.为了满足实验要求,本文使用插值算法对输入的数值矩阵进行扩充,修改两层全连接层神经元个数为2048、512,又分别采用(1)更改池化层为Max-pooling和(2)更改卷积层卷积核为3×3进行对比实验.
3 实验过程
本文使用已知的富钴结壳站点的坐标和未知区域坐标数据提取了网格型数值矩阵,对数据进行调整后,分别使用Conv-3、VGGNet 16和两个修改后的VGGNet 16结构进行对比实验.
3.1 数据来源
正样本原始数据来源于国际海底管理局(ISA)的富钴结壳主量元素标准数据集,由国家海洋科学数据共享服务平台提供.数据量共计1203站,3286个样品,空间范围覆盖全球大部分海域(-180°~180°E,-64.18°~56.17°N).剔除一些坐标分布较密集区域的坐标,实际使用1100个站点用来作为提取数值矩阵正样本的基准数据.调用Google Earth软件的API,在全球以100 km为步长提取共计12万坐标以及海拔高度信息,从中随机均匀选取15200个海拔高度在-4000~-800 m之间的坐标信息作为原始数据的负样本的基准坐标数据.在负样本中有一定的存在噪声的可能性(即可能为富钴结壳矿区),因为可能性非常小,可以认为有较高的可信度.
正负样本基准地理坐标信息被存储为26份文本,分布于26台计算机上.在每一台电脑上运行Google Earth和在Visual Studio上基于C++的数据提取程序.程序自动读取文本文件的每一个坐标(A,B),以(A,B)为中心点,以C为步长的度数表示,在 0.8~1 km2范围内从经度A-25×C到A+25×C、纬度B-25×C到B+25×C调用Google Earth软件的API提取50×50的海拔高度数值矩阵.
本文最终获得了共计16200个存储海拔高度数值矩阵的文本,其中正样本1100个,负样本15200个.因为正样本数据量过小,而地型特征具有旋转、翻转的不变性,利用这些特性将正样本的数据扩充为原来的8倍,得到8000个正样本,最终使用正负样本共计24000个地形数据.
3.2 数据处理及算法实现

图2 Conv-3 结构图Fig.2 Conv-3 schematic
对于正负样本的数据,使用文件名作为标签的标注,在程序中使用OS模块读取文件名,将正负样本分别标注为1和0.使用Numpy数值计算库以矩阵的形式读取每一个文本,对矩阵的每一个数值x1,更新数值x1= (x1-min)/MAX,更新后的数据如图3所示.
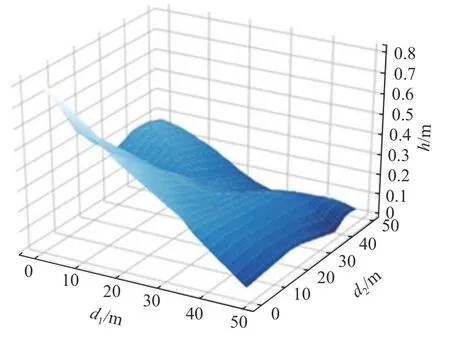
图3 处理后的数据示例Fig.3 Example terrain of processed data
此种做法针对本文实验数据存在两点优点,一是如前文所述,计算所有矩阵最大值与最小值差值,取最大差值MAX为分母,解决了使用原始方法平地和崎岖地形分不开问题;二是取得每一个矩阵的最大值max1和最小值min1,使用MAX和(max1-min1)的最大值Max为分母,防止对于新数据处理后出现矩阵大于1的情况.如图4所示,橙色表示使用min-max方法数据标准化的结果,任何矩阵都被拉伸至范围0~1,会混淆平地和陡坡,影响各矩阵相对坡度特征;蓝色表示使用统一参数MAX标准化的结果,保留了各矩阵原有的相对坡度特征不变.
另外,VGGnet 16要求数值矩阵的大小至少为48×48,且必须为3通道.为了网络模型的要求,并保证原始矩阵反应的地形特征不变,在进行对比实验时本文使用双线性插值将数值矩阵扩大为112×112,使用opencv的cvtColor函数将单通道数值矩阵转换为3通道.
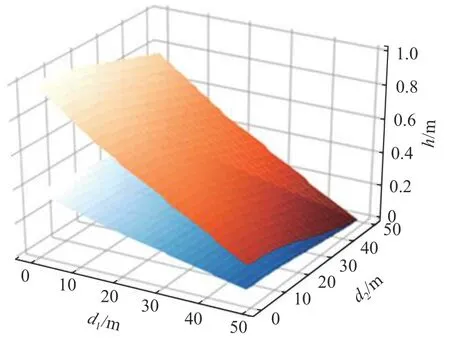
图4 同一陡坡矩阵的两种标准化结果Fig.4 Example of processed data
本文算法的实现基于python语言,使用Numpy数值计算库和Opencv计算机视觉库进行数据读入和预处理,基于深度学习高阶API Keras搭建了4种神经网络结构,实验结果的展示使用python的Matplotlib模块.
3.3 实验结果与分析
对24000个地形矩阵数值矩阵进行区分类,19200个作为训练集,4800个作为测试集,其中训练集划分20%作为验证集.本文使用多种网络结构对训练集进行训练,并对几种取得较好结果的模型效果图进行展示.
从图5来看,左图训练集和验证集的Loss值逐渐下降,右图训练集和验证机Accuracy逐渐上升,且两图曲线均呈收敛态势,说明Conv-3训练模型对已有数据是有效的.从Loss曲线可以看出在训练到65轮后验证集Loss开始高于训练集Loss且差值有扩大的趋势,产生过拟合,说明在65轮时模型取得最好效果,此时准确率为0.8246,Loss为0.415.
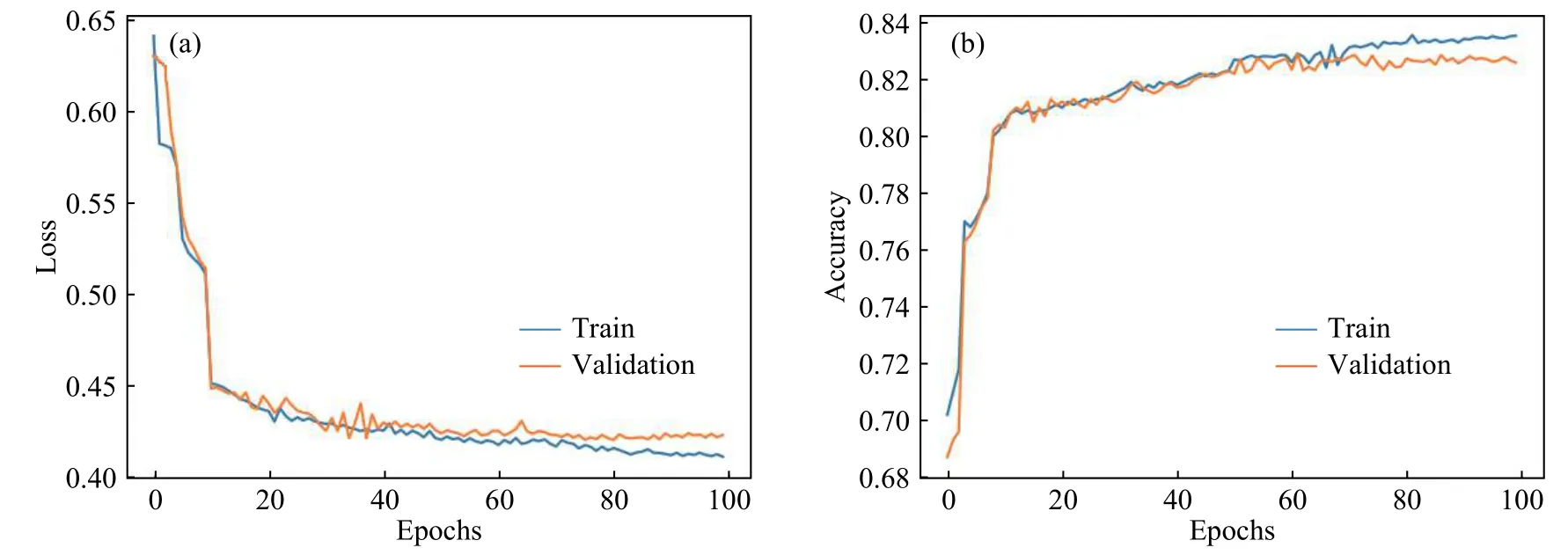
图5 Conv-3的损失曲线(a)和准确率(b)Fig.5 Conv-3 loss (a) and accuracy (b)
图6、图7和图8是使用VGGNet 16及其变式运用控制变量法进行的对比实验.和前面的Conv-3模型的结果一样,三种模型在训练集和验证集的Loss曲线和Accuracy曲线均收敛,充分证明了本文获取的地形特征数值矩阵数据集是可训练的.另外,图6和图7可以得出,VGGNet 16使用5×5和使用3×3的卷积核相比在模型准确率上更高,且收敛性更好.由图7和图8可以得出,在本文的研究中图8使用的Mean-pooling和图7使用Max-pooling相比,准确率上有所提高,模型的收敛和稳定性也较好.
使用训练得到的4种模型,在4800个测试集上进行预测,表2是预测得到的准确率的结果.可以得出,4种模型可靠性都比较高,使用VGGNet 16(5×5,Mean-pooling)上的准确率为 0.8346,分类效果最好.
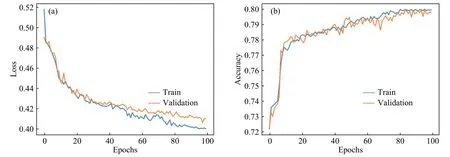
图6 VGGNet 16 损失曲线(a)和准确率(b)Fig.6 VGGNet 16 loss (a) and accuracy (b)
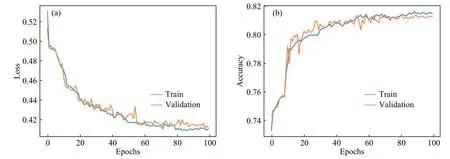
图7 VGGNet 16(5×5,Max-pooling)损失曲线(a)和准确率(b)Fig.7 VGGNet 16 (5×5, Max-pooling) loss (a) and accuracy (b)
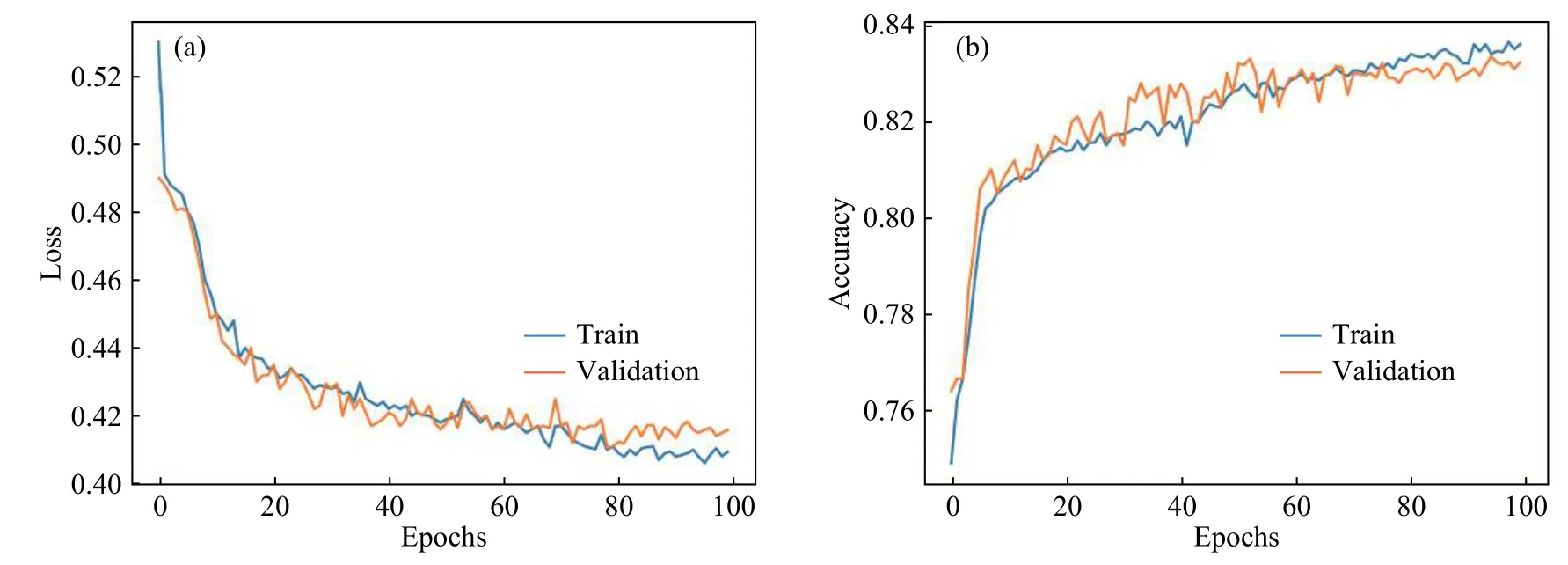
图8 VGGNet 16(5×5,Mean-pooling)损失曲线(a)和准确率(b)Fig.8 VGGNet 16 (5×5, Mean-pooling) loss (a) and accuracy (b)
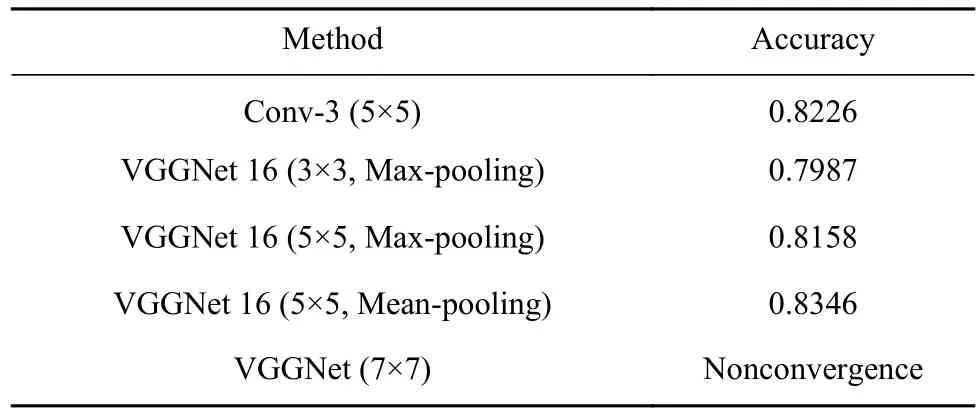
表2 实验结果Table 2 Results of experiments
从实验结果可以得到:本文从富钴结壳矿区地形特征出发,利用卷积神经网络对海拔数值矩阵训练得到预测模型.相对于已有的数据,对找矿靶点进行预测是可行的.
4 结论
(1)传统的预测方法通过一定的规则集合将专家观点、地质背景、成矿类型等因素综合考虑,影响找矿预测成果的最大因素是找矿者的先验知识.以富钴结壳矿区地形特征为出发点,运用目前非常热门的卷积神经网络模型学习特征,进行结壳矿区预测的初步研究,VGGNet 16(5×5,Meanpooling)在本文的富钴结壳地形数据集中实现较好的预测效果.
(2)通过实验结果可以得出,利用地形特征进行富钴结壳矿区进行找矿靶点预测切实可行,在准确率方面仍有提升空间.
(3)富钴结壳矿区分布受诸多因素影响.相信在不久的将来,随着数据量和精度的增加以及更深入的研究,可以把更多的影响因素放入深度学习模型当中,得到更精确的预测,可以普遍应用于勘探找矿生产环境中.
