基于最短距离调度原则的电梯群控技术研究
2021-01-04徐新仁李淑兰朱恩芳刘海峰郑萍徐东辉
徐新仁,李淑兰,朱恩芳,刘海峰,郑萍,徐东辉*
(1.南昌师范学院 数学与计算机科学系,江西 南昌330046;2.江铃汽车股份有限公司 江西省多功能乘用车工程研究中心,江西 南昌330052)
电梯作为最常用的纵向运输工具,在楼宇控制中有着不可替代的重要地位。随着当前社会高速发展,一栋大楼通常安装多台电梯才能满足乘客需求,然而当各部电梯独立运行时,则容易造成“扎堆”现象,严重影响电梯的使用效率[1]。因此需要电梯群控技术在保证环境安全、舒适的前提下,缩短乘客候梯时间,减小能量损耗。目前由PLC组成的电梯运行逻辑群控系统具有维护方便、开发周期短、可靠性高、适应性强、操作灵活等优点,现已成为电梯控制的重要发展方向[2]。
1 群控算法现状
电梯群控算法大致分两类:基于调度原则的群控和智能群控技术[3]。基于调度原则的群控主要包括分区调度原则、最小候梯时间调度原则和最短距离调度原则三个研究方向。分区调度原则包括动态分区和固定分区两种方法。动态分区外呼信号是随机的,解决了电梯忙闲不均的问题,但该算法较为复杂,且无法准确预测其响应的时间,不能进行合理分配;固定分区将导致电梯忙闲不均,运行效率较低。最小候梯时间调度原则是根据各台电梯所产生的呼梯信号,预测各部电梯响应呼梯的时间,从中选择时间最短的电梯响应呼梯信号,但该算法把停层时间和每层运行时间过于理想化,忽略手动开门信号对时间的影响。最短距离调度原则[3-4]主要是根据当前电梯位置与外呼信号位置之间的距离,通过算法选取距离最小的电梯响应呼梯信号,该算法可以解决电梯忙闲不均的弊端,有效缩短乘客的候梯时间,使电梯能量损耗降到最低。
智能群控技术主要包括遗传算法、模糊控制及神经网络等人工智能算法。遗传算法[5]主要是将候梯满意度、乘客满意度、能量损耗等因素作为评价函数协调多部电梯的运行,但在候梯时间方面考虑得较少;模糊控制算法[6-7]主要是建立在用隶属函数关系来表示数据差异状况基础理论之上所形成的,通过对电梯诸如货运、运输人力等交通方式进行分门别类划分,并依据不同的类比对电梯的控制策略予以优化,但存在模糊逻辑结果不够精确的缺陷;神经网络方法[8-9]具有网状结构,非线性问题的处理能力上较强,能对储存的信息进行合理分配,但神经网络方法精确度受样本训练数据空间大小及其精确度的影响,不能有效确保较高反应速度。
因此本文选择最短距离调度原则的电梯群控技术,对传统的最短距离调度原则群控技术进行有效的改进,经仿真验证表明本算法具有以下优点:(1)充分考虑电梯的指示与静止两种情况,克服了传统群控算法仅考虑指示情况的不足;(2)根据目标楼层与呼梯信号的距离最短原则判断电梯响应,有效缩短乘客的候梯时间,克服了传统算法在未有电梯满足条件时,通常采用等待措施的弊端;(3)本文的群控算法具有较好的普适性,梯形图清晰明了易于理解。
2 最短距离调度原则
2.1 以9楼外上呼为例进行分析
记1,2,3,4,5,6梯为A,B,C,D,E,F梯;记A,B,C,D,E,F梯当前楼层为x1,x2,x3,x4,x5,x6;
当A 梯x1≤9,且满足静止或上行指示的条件下,记y1up=9-x1;
当B梯x2≤9,且满足静止或上行指示的条件下,记y2up=9-x2;
当C梯x3≤9,且满足静止或上行指示的条件下,记y3up=9-x3;
当D 梯x4≤9,且满足静止或上行指示的条件下,记y4up=9-x4;
当E梯x5≤9,且满足静止或上行指示的条件下,记y5up=9-x5;
当F梯x6≤9,且满足静止或上行指示的条件下,记y6up=9-x6;
用博图V14min指令,记miny1up,y2up,y3up,y4up,y5up,y6up 结果为z1。
(1)当仅仅只有一个值等于z1时,无须判断优先级,立即锁定该梯响应:
z1=y1up,1梯响应;z1=y4up,4梯响应;
z1=y2up,2梯响应;z1=y5up,5梯响应;
z1=y3up,3梯响应;z1=y6up,6梯响应。
(2)当有两个及两个以上的值等于z1时(如:z1=y1up=y2up,z1=y4up=y6up),则必须考虑优先级的大小,否则将出现多部电梯响应1个信号。在此,记优先级大小为A>B>C>D>E>F,电梯响应记为1,不响应为0,易得共有2^6=64种情况[7],当A取1时,共有2^5=32种情况;当B取1时,共有2^4=16种情况;当C取1时,共有2^3=8种情况;当D取1时,共有2^2=4种情况;当E取1时,共有2^1=2种情况;当F取1时,共有2^0=1种情况;6部均取0,1种情况。32+16+8+4+2+1+1=64,检验正确,如表1所示。
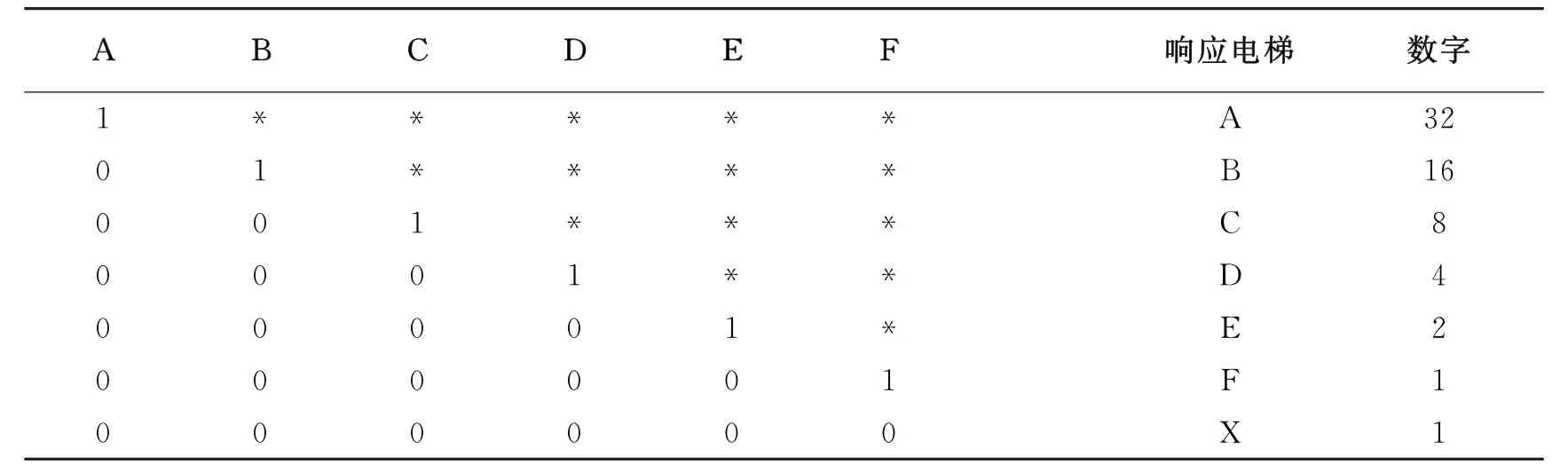
表1 6部电梯优先响应情况(*为任意值)
(3)当6部电梯均不响应时,可能6部电梯都处于下行指示状态,也可能电梯在9层上,导致响应电梯的不确定性,记X 梯响应。记A,B,C,D,E,F梯的下行目标楼层为d1(do),d2(do),d3(do),d4(do),d5(do),d6(do);记A,B,C,D,E,F梯下行目标楼层与9层的距离为L1(do),L2(do),L3(do),L4(do),L5(do),L6(do)。则L1(do)=9-d1(do);L2(do)=9-d2(do);L3(do)=9-d3(do);L4(do)=9-d4(do);L5(do)=9-d5(do);L6(do)=9-d6(do);
记min L1(do),L2(do),L3(do),L4(do),L5(do),L6(do)结果为L1(min)
当L1(min)=L1(do)时,则X=A;当L1(min)=L2(do)时,则X=B;
当L1(min)=L3(do)时,则X=C;当L1(min)=L4(do)时,则X=D;
当L1(min)=L5(do)时,则X=E;当L1(min)=L6(do)时,则X=F;
当有两个及两个以上的值等于L1(min)时,则优先级大小依然为A>B>C>D>E>F,如图1所示。
2.2 以2楼外下呼为例进行分析
当A 梯x1≥2,且满足静止或下行指示的条件下,记y1down =x1-2;
当B梯x2≥2,且满足静止或下行指示的条件下,记y2down =x2-2;
当C梯x3≥2,且满足静止或下行指示的条件下,记y3down =x3-2;
当D 梯x4≥2,且满足静止或下行指示的条件下,记y4down =x4-2;
当E梯x5≥2,且满足静止或下行指示的条件下,记y5down =x5-2;
当F梯x6≥2,且满足静止或下行指示的条件下,记y6down =x6-2;
博图V14min指令,记miny1down,y2down,y3down,y4down,y5down,y6down 结果为z2。
(1)当仅仅只有一个值等于z2时,无须判断优先级,立即锁定该梯响应:
z2=y1down,1梯响应;z2=y4down,4梯响应;
z2=y2down,2梯响应;z2=y5down,5梯响应;
z2=y3down,3梯响应;z2=y6down,6梯响应。
(2)当有两个及两个以上的值等于z2时,则必须考虑优先级的大小。同上。
(3)当6部电梯均不响应时,可能6部电梯都处于上行指示状态,也可能电梯在2层下,导致响应电梯的不确定性,记X 梯响应。记A,B,C,D,E,F梯的上行目标楼层为d1(up),d2(up),d3(up),d4(up),d5(up),d6(up);记A,B,C,D,E,F梯下行目标楼层与9层的距离为L1(up),L2(up),L3(up),L4(up),L5(up),L6(up)。
则L1(up)=9-d1(up);L2(up)=9-d2(up);L3(up)=9-d3(up);L4(up)=9-d4(up);L5(up)=9-d5(up);L6(up)=9-d6(up);
记min L1(do),L2(do),L3(do),L4(do),L5(do),L6(do)结果为L2(min)。
当L2(min)=L1(up)时,则X=A;当L2(min)=L2(up)时,则X=B;
当L2(min)=L3(up)时,则X=C;当L2(min)=L4(up)时,则X=D;
当L2(min)=L5(up)时,则X=E;当L2(min)=L6(up)时,则X=F;
当有两个及两个以上的值等于L2(min)时,则优先级大小依然为A>B>C>D>E>F,如图1所示。
3 最短距离调度原则的逻辑实现
(1)PLC 选择S7-1200 CPU1214C DC/DC/DC,工作存储器内存为7.5 K。选择EET 电梯仿真软件,PLC 与EET 软件采用通信速度快,稳定性好的Ethernet以太网通讯。PLC 的编程软件采用的是博图V14,其是西门子公司打造的集成自动化编程软件,能支持S7-1200、S7-1500、S7-300/400 控制器。
(2)当前楼层号即x1,x2,x3,x4,x5,x6的实现。第一步,电梯进行初始化,碰到上端站第二限位传感器,把11赋给楼层号标志;第二步,当上行碰到下平层传感器,则电梯楼层号加(ADD)1,如图1所示;当下行碰到上平层传感器时,则电梯楼层号减(SUB)1,如图2所示;第三步,本程序中用了FB块,当“楼层号标志==1”时,“楼层号为1标志”接通,如图3所示。
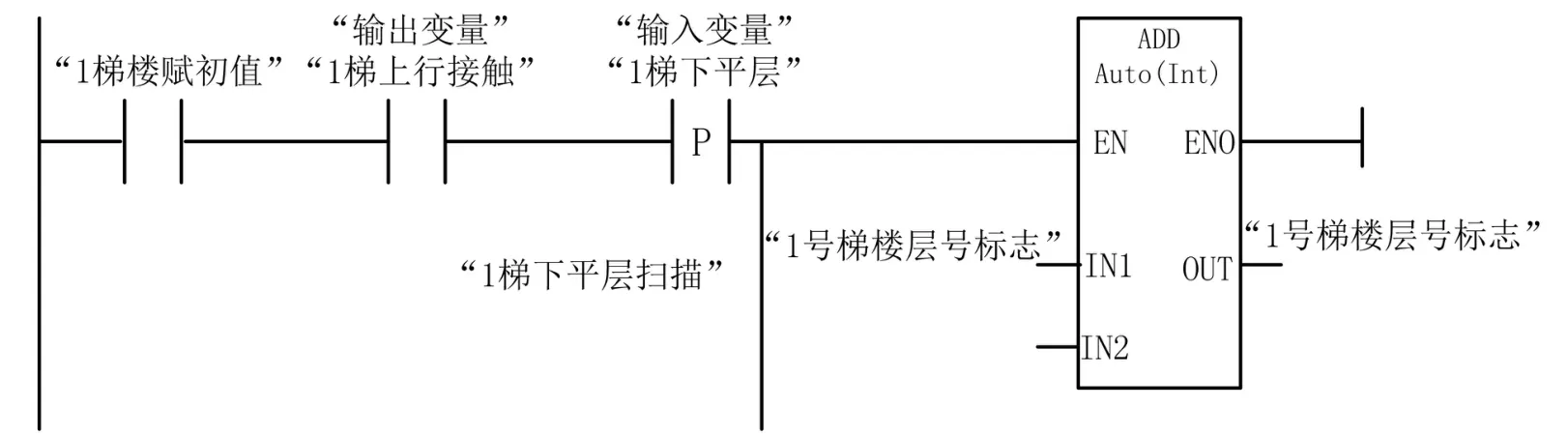
图1 上行计算当前楼层号
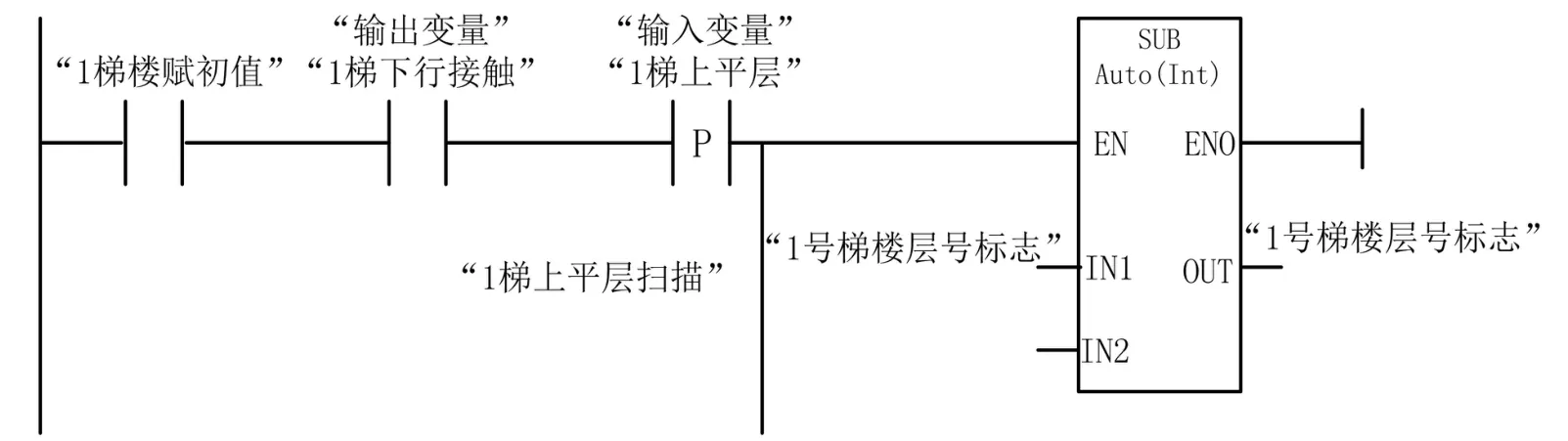
图2 下行计算当前楼层号
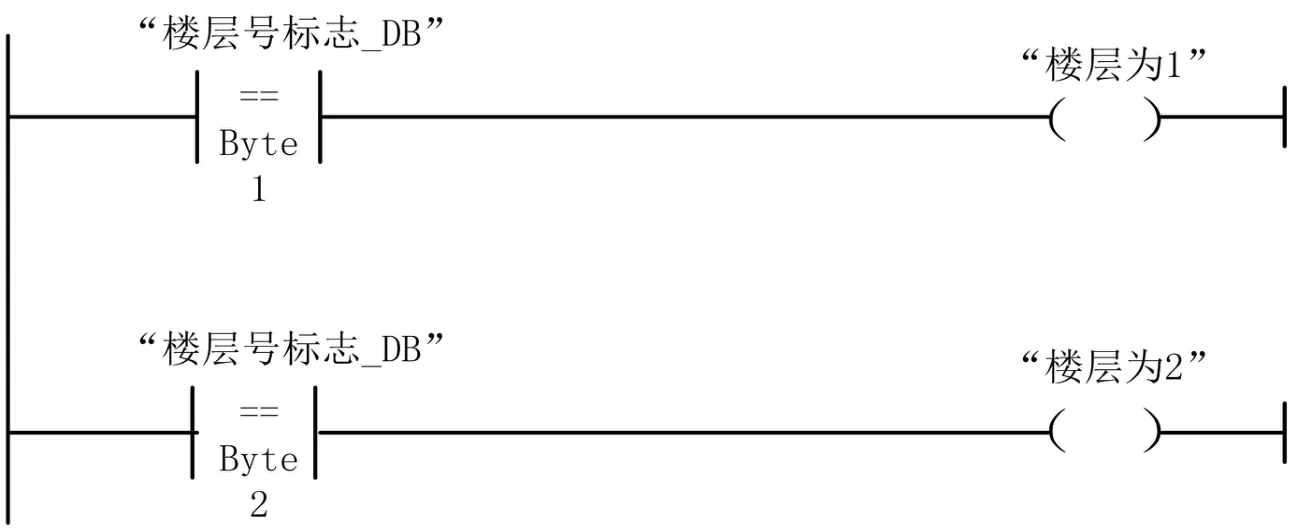
图3 当前楼层号的传递
(3)y1up,y2up,y3up,y4up,y5up,y6up的实现。第一步,只有当电梯楼层号小于9时方可计算;第二步,静止,上行指示为或关系;第三步,计算环节:9-“1号梯楼层号标志”=“梯1距9数上”。如图4所示,显然,y1up即为“梯1距9数上”,同理可求y2up-y6up。
(4)z1的实现。MIN 指令左边的输入端口IN1,IN2,IN3,IN4,IN5,IN6,即为y1up,y2up,y3up,y4up,y5up,y6up。输出OUT“距9位置差最小上”即为z1的值,如图5所示。
(5)优先级的实现。即A>B>C>D>E>F。
当A 响应时,梯形图中“用1梯标志1”为1;
当B响应时,梯形图中“用2梯标志1”为1;
当C响应时,梯形图中“用3梯标志1”为1;
当D 响应时,梯形图中“用4梯标志1”为1;
当E响应时,梯形图中“用5梯标志1”为1,如图6所示。
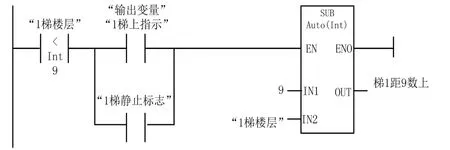
图4 计算1号梯距9层距离
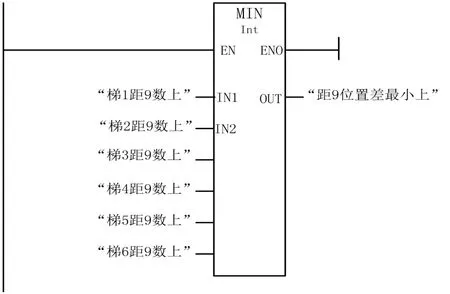
图5 计算6部梯离9最近数值

图6 优先级的实现
4 结语
(1)针对电梯群控多目标、非线性、不确定性等特点,采用最短距离调度原则对现有电梯群控算法进行了改进,针对电梯当前楼层与呼梯楼层距离问题,充分考虑了电梯静止的情况,弥补了传统算法仅考虑指示情况的不足。
(2)通过西门子S7-1200PLC控制,在博图软件上编写程序,实现了最短距离调度算法。经EET 仿真验证了该算法的平均候梯时间较短,整体效果较好。
(3)调度算法无须建立精确的模型,具有较强的普适性,对于电梯群控设计具有一定现实指导意义。
(4)人工智能已经与电梯群控技术牢牢结合,使电梯的自动化运行及调度更加安全、合理、人性化,高度智能化的电梯群控系统研究将是未来电梯研究的主要方向。
