基于最大衰减因子模型的服装热防护性能预测

何佳臻，薛萧昱，王 敏，李 俊

(1. 苏州大学 纺织与服装工程学院，江苏 苏州 215021； 2. 苏州大学 现代丝绸国家重点实验室，江苏 苏州 215021； 3. 东华大学 现代服装设计与技术教育部重点实验室，上海 200051)

消防救援、工业冶金、军事反恐等行业的从业人员经常遭受各种潜在的环境热灾害，包括爆炸烈火、高温热辐射、熔融金属、热蒸汽或热气体等。热防护服装是保护作业人员免受各类环境热侵袭的必备个体防护装备，其热防护功能的不足将引起皮肤烧伤，甚至对作业人员的生命安全造成严重威胁。根据美国消防协会的资料，2015年仅在消防救援中，遭受皮肤烧伤的作业人员达到2 020名[1]。在热灾害环境下，充分发挥防护服装的热防护功能是保障作业人员生命安全和有效执行任务的唯一途径。

如何准确全面地评价防护服装的热防护性能对于科学装备防护服装、机构产品研发、产品控制及用户产品选择具有重要作用。目前防护服装的热防护性能评价主要采用织物试样测试与燃烧假人轰燃实验，它们各有优缺点。总体而言：织物试样测试具有测试成本低、实验可控性好、实验效率和测量精度高等优点；燃烧假人轰燃实验可通过对灾害环境下仿真人体的烧伤程度评估，获取服装整体热防护性能信息，但该方法不仅要求具备价格高昂的燃烧假人测试系统，而且需要对完整服装进行破坏性实验，因此测试成本很高，实验效率较低且可重复性相对较差[2]。为此，实现基于织物试样测试的防护服装热防护性能预测，对于降低测试成本、节约资源具有重要意义。

近年来，防护服装热防护性能的评价原理突破发展。研究表明，热防护服装实际上对人体皮肤存在截然相反的双重作用[3]：一方面，在热危害暴露阶段通过阻隔环境热发挥了热防护的作用；另一方面，在热危害暴露结束后通过向人体皮肤不断释放蓄热又实施热危害作用。长期以来，防护服装领域广泛使用的热防护性能(TPP)、耐热辐射性能(RPP)测试等，均仅评估了热暴露阶段防护服装的隔热防护作用，却忽略了离开热源后其对人体皮肤产生的放热危害作用，这会对评价结果的全面性造成影响，也会高估甚至是误判了防护服装的真实热防护性能，对防护服装的可靠性造成挑战。

目前，在织物试样测试和假人轰燃实验方面均已分别建立了相关测试方法用于评价热防护服装对人体皮肤的双重作用，但是现有的织物试样测试和燃烧假人实验仍存在较大差异性和局限性。首先，二者的测试原理和测试程序不同。假人轰燃实验采用固定热暴露时间法，例如ISO 13506∶2008《防热和防火防护服·完整服装的试验方法·用装备假人对燃烧伤害的预测》建议单层热防护服装的热暴露时间为3 s或4 s，而双层服装的热暴露时间为4 s或5 s，以最终考察衣下皮肤在整个数据采集时间段内所能引发的烧伤程度。而织物试样测试则要求将织物持续暴露于闪火热源中直至皮肤达到二级烧伤为止。为与假人轰燃实验程序进行统一，Schoppee等[4]也曾尝试设置相同的热暴露时间，将不同织物暴露于闪火热源中，但发现最终只能判断衣下皮肤是否达到了二级烧伤，而不能进一步区分不同织物的热防护等级。其次，二者的评价指标不同。假人轰燃实验最终获得的是人体皮肤烧伤图谱，显示了人体烧伤分布和烧伤百分比；但织物试样测试的输出结果为衣下皮肤达到二级烧伤的时间。另外，也需注意，2种方法中所使用的烧伤预测模型不同。织物试样测试普遍采用Stoll二级烧伤准则作为皮肤烧伤的阈值，而假人轰燃实验采用Henriques烧伤积分模型。研究发现，这2种烧伤评价方法可能导致不同的烧伤预测结果[5]。上述差异最终造成了平面织物与立体服装间的测试结果不能直接进行比较，因此，长期以来绝大多数研究均是针对织物和服装分别展开。20世纪90年代起开展了针对织物试样和假人轰燃实验的比较研究，但也仅进行了简单的关联性分析[6-7]。可以看出，传统的评价方法无法完成对织物试样和服装整体热防护性能的统一联合表征，这也成为了实现基于织物性能测试的防护服装热防护性能预测的瓶颈问题。

文献[8]提出了一种新型的热防护性能评估模型：二级烧伤最大衰减因子(MAF)模型。首先该模型从皮肤烧伤预测角度，全面评价了热防护织物或服装对人体皮肤的热防护和热危害双重作用；最重要的是，该模型统一了织物试样测试和服装整体测试的实验程序和评价指标，使得织物和服装的测试结果可以直接进行比较，这为实现基于织物试样测试的服装整体热防护性能预测提供了实践基础。本文将利用MAF评价模型，首先对防护织物和服装的MAF评价结果关联性进行探讨，然后利用MAF评价模型，建立基于织物试样测试的防护服装热防护性能和皮肤烧伤预测模型，为热防护服装的性能评价提供更有效、更具成本效益的手段。

1 实验设计

1.1 实验面料

本文研究选用了9种当前市场上常用的热防护服装面料，利用这些面料共制成符合标准要求的统一规格服装试样。参照ISO 13506∶2008对实验服装的款式和规格进行设计。服装款式为上下连体式，腰部有横向分割线设计，前中门襟有拉链开口，衣领为立领，衣袖为直身袖。实验服装的基本规格符合标准尺寸175/96A。测试服装面料的性能如表1所示。这些服装代表了不同的热防护等级，可分为单层服装和多层服装，其中单层服装G1～ G7用于森林火灾战斗灭火服、工业和军事防护服，多层面料服装G8和G9用于建筑火灾消防战斗服，该类服装包含外层、防水透气层和隔热层。

1.2 燃烧假人实验的实施

本文实验采用“东华火人”燃烧假人测试系统，该系统满足ISO 13506∶2008的相关技术要求。假人本体尺寸符合中国男性体型，身高为175 cm。假人表面均匀设置了135个传感器，可对闪火全程假人体表温度和热流数据进行实时采集。实验时燃烧室内的模拟热暴露环境为(84±2) kW/m2，由6组 12个喷火头提供，燃烧器均匀分布在假人周围。通过燃烧假人测试，可预测各传感器部位的皮肤烧伤程度以及人体烧伤百分比，进而实现对服装整体热防护性能的综合评估。

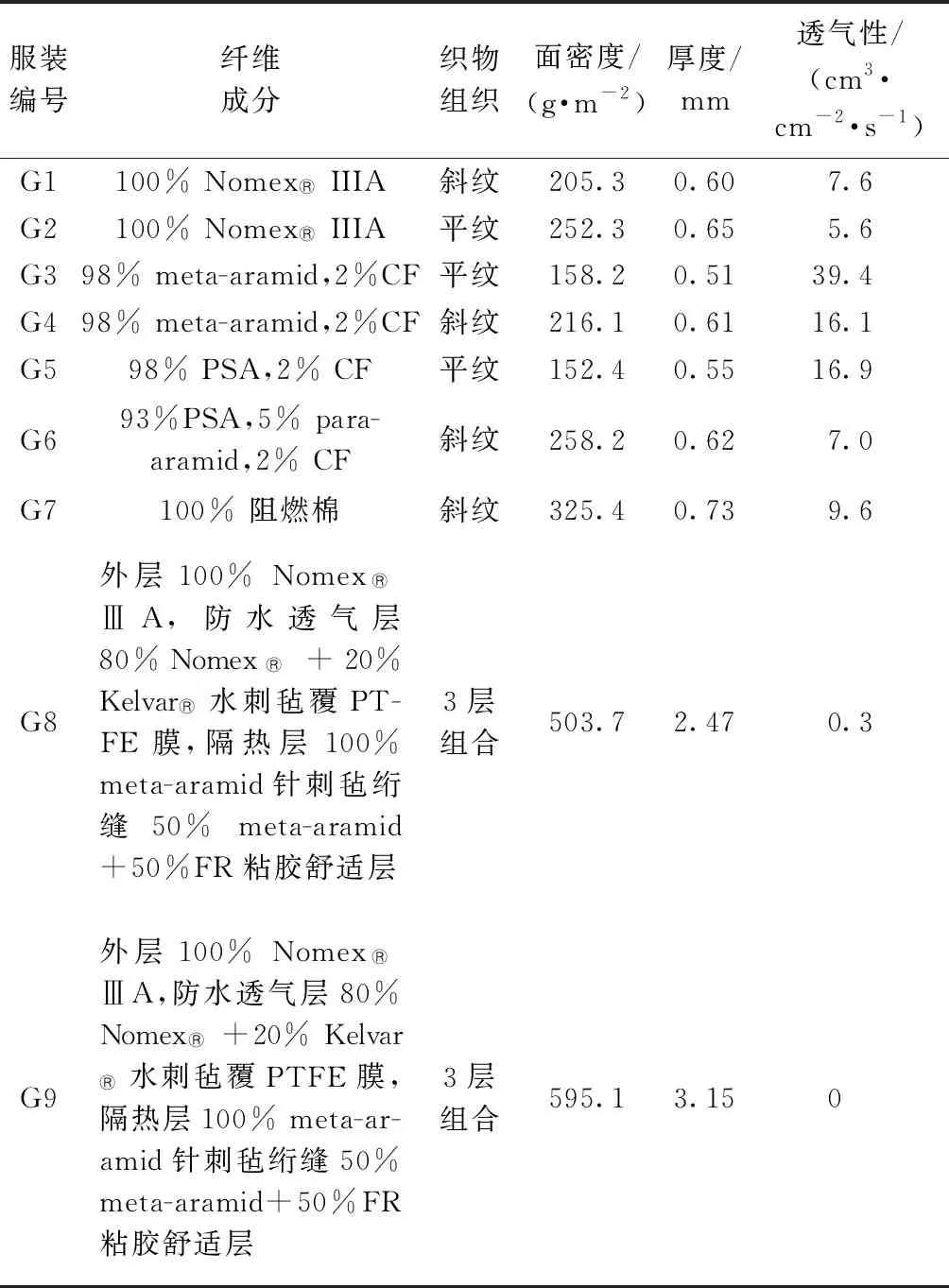
表1 实验面料的基本性能Tab.1 Specifications of fabric

对于单层服装，参考ISO 13506∶2008标准将热暴露时间设置为4 s；对于多层服装，热暴露时间设置为6 s。为评估热暴露结束后服装的蓄热释放作用，传感器的数据采集时间应包含热暴露结束的冷却阶段。参考测试标准，单层和多层服装的数据采集时间分别设定为60 s和120 s。

1.3 织物试样测试方法

采用织物热防护性能测试仪CSI-206(美国)对实验服装所采用的对应面料进行测试。模拟火场环境由2个Meker燃烧器(与测试织物成45°)和9个石英灯管提供，它们所产生的热流密度与燃烧假人实验相同，为(84 ± 2) kW/m2。织物试样架和热源间设置了电子触发式气动水冷遮板，可在热暴露前将织物与热源隔绝并准确控制热暴露时间。铜片热流计采用直接接触的方式置于织物背面，测量模拟皮肤位置的温度。与燃烧假人实验相同，单层和多层织物试样的热暴露时间分别设置为4 s和6 s。热暴露结束后，将试样推车移离热源，持续采集传感器数据，直至单层织物和多层织物的总数据采集时间分别达到60 s和120 s。通过上述步骤，统一了织物试样测试和燃烧假人实验的测试程序。

1.4 热防护性能评价新模型

1.4.1 织物热防护性能评价

采用MAF评价模型[8]，评价织物和服装的热防护性能。该模型可用于判断在传热全程中传感器的能量响应与Stoll皮肤烧伤准则的关系。该模型将铜片热流计所吸收的热量Q(t)与根据Stoll准则预测的皮肤达到二级烧伤所需热量S(t)进行逐时比较，并计算数据采集总时间tT内Q(t)与S(t)比值的最大值：

(1)

式中，εMAF为二级烧伤最大衰减因子，为无量纲量。

事实上，织物热防护性能测试中铜片热流计记录的是传感器的温度变化，根据ASTM F2703—2008《基于烧伤预测的阻燃服装材料非稳态传热评估的标准试验方法》，可将该温度转化为传感器所吸收的热量，即式(1)中的Q(t)，其计算公式为：

(2)

式中：Q(t)为t时间内铜片热流计所吸收的热量，kJ/m2；M为铜片热流计的质量，g；Cp为升温过程中铜片的平均比热容，kJ/(g·℃)；A为铜片热流计的表面积，m2；Ti和Tf分别为铜片热流计的初始温度和t时刻的温度，℃。需注意，式(2)忽略了传感器背面和周围由于热传导所引发的热量散失。

此外，式(1)中所涉及的Stoll烧伤准则反映了皮肤吸收能量与二级烧伤的时间关系。自2008年开始，美国材料与试验协会在新版的ASTM系列标准中[9]，将Stoll准则作为皮肤二级烧伤的阈值，其可按照式(3)进行计算：

S(t)=50.204t0.290 1

(3)

式中：S(t)为根据Stoll准则预测的皮肤在t时刻达到二级烧伤时所吸收的能量，kJ/m2；t为热暴露开始后所经历的时间，s。

图1示出织物试样测试时传感器的能量响应曲线与Stoll准则曲线的示意图。从MAF的计算原理可以看出，MAF评价模型评估的是传热全程皮肤烧伤的最大危险性。若εMAF值小于1.0，则表示传感器所吸收能量不足以引起皮肤二级烧伤；若εMAF值刚好为1.0，则表示传感器所吸收能量刚好达到皮肤烧伤的阈值；若εMAF值大于1.0，则表示传感器的能量响应曲线会超过Stoll准则曲线，皮肤达到二级烧伤。

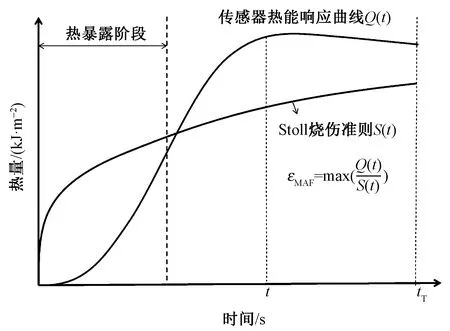
图1 传感器能量响应曲线和Stoll准则曲线示 意图以及MAF的计算示例Fig.1 Schematic representations of sensor response and Stoll criteria, and determination of MAF

1.4.2 服装热防护性能评价

MAF模型同样适用于燃烧假人测试。在燃烧假人测试中，假人表面第i个传感器所对应部位的服装局部二级烧伤最大衰减因子(εMAFi)的计算式为：

(4)

式中：S(t)为根据Stoll准则预测的皮肤在t时刻达到二级烧伤时所吸收的能量，kJ/m2,可按照式(3)进行计算；Qi(t)为假人表面第i个传感器在t时间内所吸收的能量，其计算式为：

(5)

式中：qi(t)为t时刻假人表面第i个传感器的热流密度，kW/m2；Δt为采样时间间隔，s。

服装整体二级烧伤最大衰减因子(εOMAF)的计算如式(6)所示：

(6)

式中：Ai为第i个传感器所代表的假人体表面积，m2；A为假人体表总面积，m2；n为假人体表传感器数量。由于实验中假人头部、手和脚未被服装覆盖，这些部位不纳入计算。

2 结果与讨论

2.1 织物试样实验和假人着装实验的关系

首先对织物试样测试和假人着装实验结果的关联性进行分析。服装的εOMAF值与织物的εMAF值关系如图2所示。可知，实测织物试样的εMAF值与其服装整体的εOMAF值呈显著线性正相关关系(P< 0.01)，拟合方程可决系数R2=0.764，表明织物试样测试结果与服装整体的测试结果具有显著的相关性。这为进一步建立基于织物试样测试的服装整体热防护性能预测模型奠定了基础。

图2 实测服装εOMAF值和织物εMAF值的相关性Fig.2 Correlations between experimental εOMAF of garments and εMAF of fabrics

2.2 服装整体热防护性能预测模型建立

服装对人体皮肤的热防护性能不仅取决于面料的热防护性能，而且还与服装的结构设计和测试条件有关。衣下空气层厚度是反映服装结构设计特征的主要参数[10]，而热暴露时间是测试条件的主要可控参数。因此在建立服装热防护性能预测模型时，选取无空气层状态下织物的εMAF值、服装平均衣下空气层厚度和热暴露时间作为模型输入参数，分别表征织物的热防护性能、服装结构特征以及测试条件因素。其中，服装平均衣下空气层厚度的测量可采用三维人体扫描技术，获取着装和裸体状态的三维点云数据，进而计算服装衣下空气层的平均厚度εTAG值，具体方法请参见Wang等[11]的研究。利用多元线性回归方程建立服装整体的εOMAF值预测模型，如式(7)所示。模型的可决系数R2=0.921，显著性水平P< 0.001，说明因变量的方差中，自变量能解释92.1%，模型具有较好的拟合优度。

(7)

式中：εOMAFpre为服装二级烧伤最大衰减因子的预测值；εMAFtest为面料二级烧伤最大衰减因子的实测值；εTAG为服装平均衣下空气层厚度的实测值；texp为热暴露时间的预设值。需注意，在获得εTAG值的过程中，并不需要开展实际的燃烧测试，只需采用具有与人体形态一致的模型(例如人台、暖体假人、燃烧假人)进行三维扫描测量即可。此外，Texp可根据实际情况进行直接设定，例如参考ISO 13506∶2008标准将单层服装的热暴露时间设置为3 s或4 s，在设定了服装的texp值之后，需确保在织物试样测试中采用相同的热暴露时间，以获得在相同测试条件下织物的实测εMAF值，进而利用式(7)进行预测。

基于上述预测模型，图3比较了模型预测值与实验测量值的关系。进一步采用平均绝对百分比误差(EMAPE)对预测模型的准确性进行评价，如式(8)所示[12]。模型的平均绝对百分比误差仅为4.82%，说明模型具有较高的预测精度。

(8)

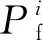
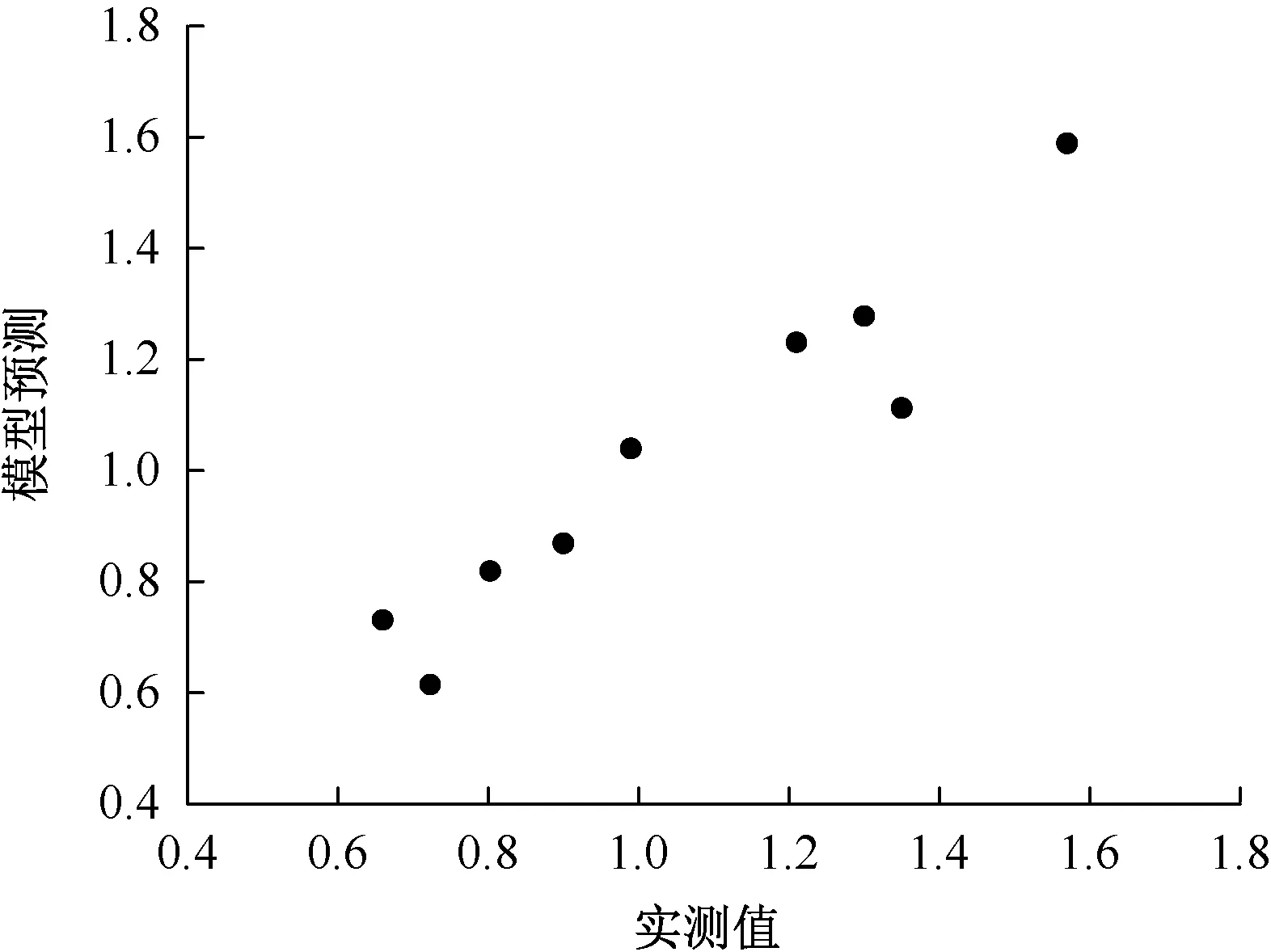
图3 服装εOMAF的实测值与预测值比较Fig.3 Comparison of measured and predicted εOMAF of clothing

传统燃烧假人测试的评价指标为皮肤烧伤百分比，即达到皮肤烧伤的面积占皮肤总面积的百分比程度。利用MAF评价模型，同样可对皮肤烧伤百分比进行预测。根据MAF模型的评价规则可知，当εMAF值大于或等于1.0时，则表示皮肤会达到二级烧伤。在燃烧假人测试中，通过预测假人表面所有传感器位置的εMAF值并判断其是否大于或等于1.0，进而可计算皮肤的二级烧伤百分比，如式(9)所示。

(9)

式中：PTBP为二级烧伤的百分比，%；Ai，εMAF≥1为εMAF值大于等于1.0时，假人第i个传感器所代表的假人体表面积，m2；A为假人体表总面积，m2；n为假人体表传感器数量。实验中假人头部、手和脚这些部位不纳入计算。

图4示出假人着装实验中服装的εOMAF值与皮肤烧伤百分比之间的关系，其回归方程如式(10)所示。方程的可决系数R2=0.960，该回归方程适用于服装的εOMAF值大于0.4的情况。

PTPB=(75.337εOMAF-30.591)×100%

(10)

式中：PTBP为二级烧伤百分比，%；εOMAF为服装的二级烧伤最大衰减因子。

图4 服装εOMAF值与人体皮肤烧伤百分比的关系Fig.4 Relationship between εOMAF of clothing and percentage of burn injury in manikin test

联合方程(7)和(10)，即可实现基于织物试样测试的燃烧假人烧伤百分比预测，其方程如式(11)所示。

(11)

式中：εTBPpre为二级烧伤百分比的预测值，%；εMAFtest为面料二级烧伤最大衰减因子的实测值；εTAG为平均衣下空气层厚度的实测值；texp为热暴露时间的预设值。

2.3 预测模型验证

本文另选择面密度为205 g/m2的100% Nomex©IIIA面料，验证上述服装热防护性能和皮肤烧伤百分比预测模型的准确性，该验证实验的热暴露时间设置为3 s。

利用织物热防护性能测试仪测量实验织物的εMAF值，为1.18。按照前文所述的服装款式和规格制作服装，并将实验服装穿着于“东华火人”燃烧假人本体上，采用三维人体扫描仪获取服装平均衣下空气层厚度信息。利用式(4)和(8)分别预测服装的εOMAF值和衣下皮肤烧伤百分比。为验证预测模型的准确性，还需实际测量燃烧假人实验中服装的εOMAF值和衣下皮肤烧伤百分比。

表2示出了模型预测值和实验测量值的对比结果。可以看出，服装εOMAF的预测值和实测值分别为0.62和0.59，二者间的相对误差仅为5.1%。同时，烧伤百分比的预测值(16.5%)和实测值(14.3%)相对误差为15.4%，但是其绝对误差仅为2.1%。虽然烧伤百分比的相对误差相对较大，但结果是可接受的，这是因为相较织物测试而言，燃烧假人测试在实际测量时的可重复性较差[2]，研究表明燃烧假人测试时皮肤烧伤百分比的标准偏差范围为5.4%～37.1%[13]，而本研究中实测值与预测值的偏差仅为2.1%，由此可见所建立模型仍具有较高的预测精度。

表2 服装热防护性能预测值和实测值比较Tab.2 Comparison of predicted and experimental results of clothing thermal protective performance

3 结 论

虽然近年来在织物试样测试和假人轰燃实验方面均已分别建立了相关测试方法用于评价热防护织物或服装对人体皮肤的双重作用，但是现有的织物试样测试和燃烧假人实验仍存在较大差异性，主要表现在测试原理、测试程序不同以及评价指标不同。传统的测评方法无法完成对织物试样和服装整体热防护性能的统一联合表征，这也成为实现基于织物性能测试的着装人体皮肤烧伤预测的瓶颈问题。

本文利用二级烧伤最大衰减因子评价模型，实现基于织物试样测试的防护服装热防护性能预测，为热防护服装的性能评价提供更有效、更具成本效益的手段。主要得到以下结论：1)织物试样测试的εMAF值与燃烧假人轰燃实验的εOMAF值呈显著的线性正相关关系；2)基于二级烧伤最大衰减因子评价方法建立了服装热防护性能预测模型，经验证该模型具有较好的预测精度。利用织物试样测试的εMAF值、服装平均衣下空气层厚度和热暴露时间，可对服装整体的热防护性能εOMAF值以及烧伤百分比进行直接预测。