基于两级奇异值分解的鲁棒水印算法

陈 青，夏兰婷，卜 莹

上海理工大学光电信息与计算机工程学院，上海200093

由于通信技术、网络技术和计算机技术的飞速发展，数字媒体得到了广泛的应用与发展.目前，数字媒体主要通过网络传输信息.然而，开放的网络环境也给数字作品的信息安全和版权保护带来巨大挑战[1].作为一种安全有效的保护数字版权的技术手段，数字水印技术广泛应用于数字媒体领域[2].

文献[3-4]将奇异值分解的稳定性、缩放不变性运用于图像增强的领域，取得了一定的成果.文献[5]针对医学图像的特征以及医学图像与患者文本信息的相关性，提出一种基于奇异值分解（singular value decomposition, SVD）的水印算法.文献[6]将SVD 分解与离散小波变换（discrete wavelet transform, DWT）结合使用，可减少空域图像里SVD 分解带来的较大运算量.文献[7]基于DWT 和SVD，提出一种鲁棒性较好的的视频水印算法.文献[8]提出一种基于SVD 和DWT 的人类视觉系统的块水印算法，选取边缘熵最小的块作为水印的嵌入区域.文献[9]改进了常规的DWT-SVD 域的水印算法，选择遗传算法来寻求最佳比例系数，平衡了载体的不可见性和鲁棒性.上述几种方法均采用了SVD 分解技术，而矩阵的奇异值具有旋转、缩放不变性，在一定程度上增强了图像的鲁棒性.但单独使用1 次SVD 分解来嵌入水印，对载体的破坏较大.由于奇异值矩阵(1, 1)处的值所包含的能量最高且同步影响较小，本文选择第1 级SVD 变换后坐标为(1, 1)处的奇异值构建特征矩阵，该奇异值特征矩阵继承了载体的主导特征.

现有的水印算法抵抗旋转攻击的能力明显不足，主要的解决方案是在水印提取前进行校正.文献[10]计算出了数字矩阵的Radon 变换不变矩，利用少量低阶Radon 不变矩构建零水印信息.文献[11]提出了一种新的且可靠的基于SVD 和IWT 的图像水印方案，将水印的S和V矩阵用作秘密密钥，水印的奇异向量嵌入主图像的奇异值.文献[12]利用Radon 变换校正待检测图像，提高水印算法的抵抗旋转攻击的能力.文献[13]利用Harris 角点提取原始图像特征点，选取特征区域，然后利用伪Zernike 矩的相位信息对图像进行旋转校正，可有效抵抗旋转攻击.通过上述方法旋转校正后的图像虽能抵抗该攻击，但仍然存在像素值缺失而导致水印值缺失的情况.因此，本文选取旋转后像素近似无损的正方形区域进行水印嵌入，以减少像素的缺损现象，同时保证水印的嵌入容量.

本文提出一种新的基于旋转稳定区域和两级SVD 分解的鲁棒水印算法.本算法选取像素无损的稳定区域进行水印的嵌入，提取水印时用Radon 变换进行校正，保证水印的嵌入容量，增强抵抗旋转攻击的能力.针对常规一级SVD 分解对载体的破坏性较大而导致鲁棒性较差的问题，本文将低频部分SVD 分解后提取第1 个奇异值构建特征矩阵，然后再进行SVD 分解以实现水印嵌入.该方案不仅保证了水印的嵌入容量和不可见性，而且还提高了水印抵抗几何攻击的能力.

1 基本原理

1.1 两级奇异值分解（SVD）

假设图像A是一个N×N的矩阵，那么存在N ×N矩阵U和V，使得

式中，Σ=diag(σ1,σ2,···,σN)是一个对角矩阵，也被称为A矩阵的奇异值，具有抵抗几何攻击和信号攻击的能力.奇异值矩阵的系数大小为，其第1 行和第1 列的值σ1大于其他奇异值，表示σ1具有最大的能量压缩，受同步影响也比较小[14].奇异值矩阵可以写为

选取σ1构建特征矩阵，并再次对所得的特征矩阵进行SVD 分解.两级奇异值分解既保留了载体图像的最大能量信息，又减少了对原始图像的破坏，增强了不可见性.

奇异值代表图像的亮度信息，改变奇异值并令Σε=εΣ，则

若0<ε<1，则A变暗；若ε>1，则A变亮.对于ε>0，令Σε=Σ+ε，则

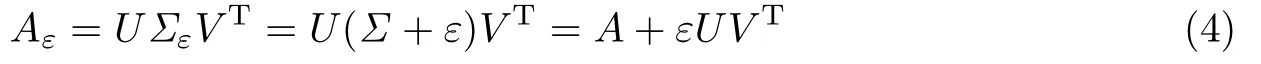
矩阵εUVT值很小，与较大的A值对比可忽略.

图像奇异值分解后大部分数据信息存储在正交矩阵U和V中，图像对U和V的改变较敏感.若令Uε=U+ε，则

矩阵εΣVT是一个数值较大的矩阵，对图像影响大，故本文选择在奇异值上运用加性原则进行水印的嵌入.

1.2 旋转稳定区域

常规的抵抗旋转攻击的方法有两种：一种是在具有旋转不变性的特征区域进行水印嵌入，如SIFT 或SURF 特征点；另一种是对含水印信息的载体图像进行旋转校正，如SURF 旋转校正和Radon 校正，也就是先对已旋转的载体图像进行1◦∼359◦的角度校正，然后再进行水印提取.在特征区域嵌入水印会导致嵌入量的减少，而旋转校正后的图像边缘信息会存在缺失，即使校正也无法弥补之前缺失的像素部分.将图像进行15◦、45◦、75◦、90◦、125◦、145◦的不同角度旋转，得到的图像如图1所示.

图1 旋转攻击后的图像Figure 1 Image after rotation attack

利用Radon 变换后的的旋转校正结果及像素缺失情况见表1.

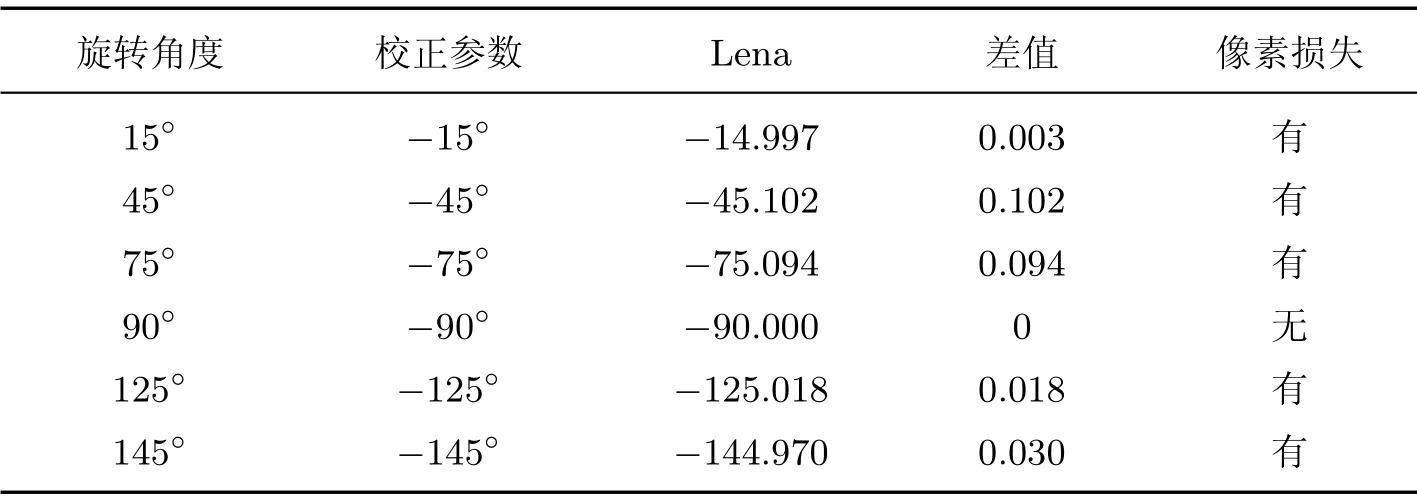
表1 旋转攻击后的旋转校正结果及损失情况Table 1 Rotating correction results and loss after rotation attack

旋转后图像的边缘信息会受到一定的损失，若水印嵌入在完整图像中，那么边缘水印信息也会损失.当旋转角度为45◦时图像损失面积最大，所以在旋转45◦的图像中选择旋转稳定区域，可以保证当旋转其他角度时图像损失最小.选取图1（b）旋转45◦后的内接正方形区域为内接旋转稳定区域，该区域里的像素值不会因旋转角度的不同而丢失.为了验证所选区域在旋转之后是否出现像素数据损失的情况，将载体图像经过各种角度旋转，再进行Radon 校正，得到的攻击效果（正常情况下内切正方形的规模）如图2所示.可见，含水印的载体图像经旋转后其水印嵌入区域仍保持稳定，并无任何像素损失，因此内切正方形区域适合作为水印的嵌入区域.

图2 校正后的旋转稳定区域Figure 2 Corrected rotational stable zone

1.3 Radon 变换

Radon 变换是某个方向上图像的线积分，对于可能受到的旋转攻击有同步性.二维图像f(x,y)的Radon 变换即为图像矩阵在特定角度射线方向上的投影，公式为

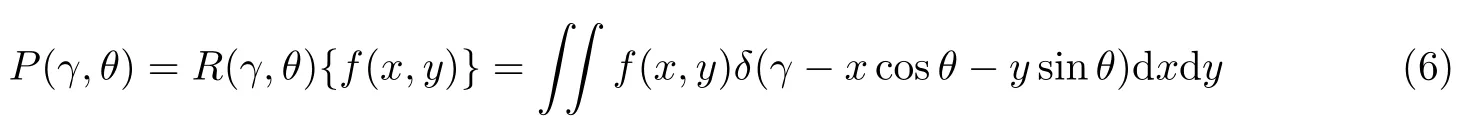
式中，γ为坐标原点到直线的距离，θ为直线与轴的夹角.函数δ为f(x,y)沿直线γ=cosθ+sinθ的积分，目的是获得在任意(γ,θ)处f(x,y)沿着该直线的投影.变换示意图见图3.

图像的校正步骤如下：

步骤1对载体图像进行0◦的Radon 变换得到R0，并将R0送到版权保护中心注册保存，校正时只需与R0进行对比.

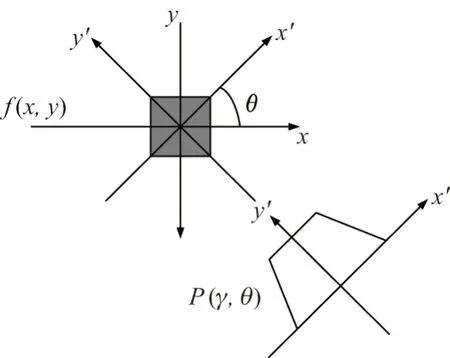
图3 Radon 变换Figure 3 Radon transform

步骤2待检测图像进行0◦∼179◦的Radon 变换，校正增量为1◦，得到180 个检测向量R(θ)，θ ∈[0◦,1◦,···,179◦].

步骤3按照式（6）计算R(θ)与R0的相关系数，得到旋转度数

步骤4对载体按照步骤3 计算的旋转角度进行逆旋转，对颠倒的图像内容进行校正，得到校正后的含水印图像.

2 水印的嵌入和提取

2.1 水印的嵌入

如图4所示，水印嵌入的基本步骤如下：

步骤1根据第1.3 节介绍的方法确定图像中的旋转稳定区域T，大小为M×M，保存其左上角坐标和边长.

步骤2对大小为M×M的旋转稳定区域T进行一层冗余离散小波变换（redundant discrete wavelet transform, RDWT），提取低频分量LL.

步骤3将低频分量LL 分为不重叠的8×8 的像素块，每一个分块的系数矩阵记为Hi.

步骤4对分块Hi分别进行奇异值分解，即

式中，Ui为正交矩阵，Si为对角矩阵.

步骤5选取分块Hi奇异值的第1 行第1 列数值Si(1,1)，构建特征矩阵O，在提取水印时只需要此矩阵信息即可实现盲提取.

步骤6对矩阵O进行二次SVD 变换，计算公式为O=UO×SO×VTO.

步骤7对水印W进行一级DWT 和SVD 分解，计算公式为W=UW ×SW ×VTW.

步骤8将水印图像中的SW与缩放因子α相乘，添加到图像二级奇异值，计算公式为=So+α×SW.

步骤9逆SVD 得到特征矩阵，计算公式为

步骤10的每个元素都带有(1,1).因此，每个来自矩阵的元素将被替换为每个8×8 块的S系数的第1 个元素，新SVD 矩阵为Si(1,1)(1,1).

步骤11对每个矩阵的新奇异值系数与其左右向量进行逆SVD 得到分块信息，再将合成的分块进行逆RDWT 变换，得到含水印图像T∗.

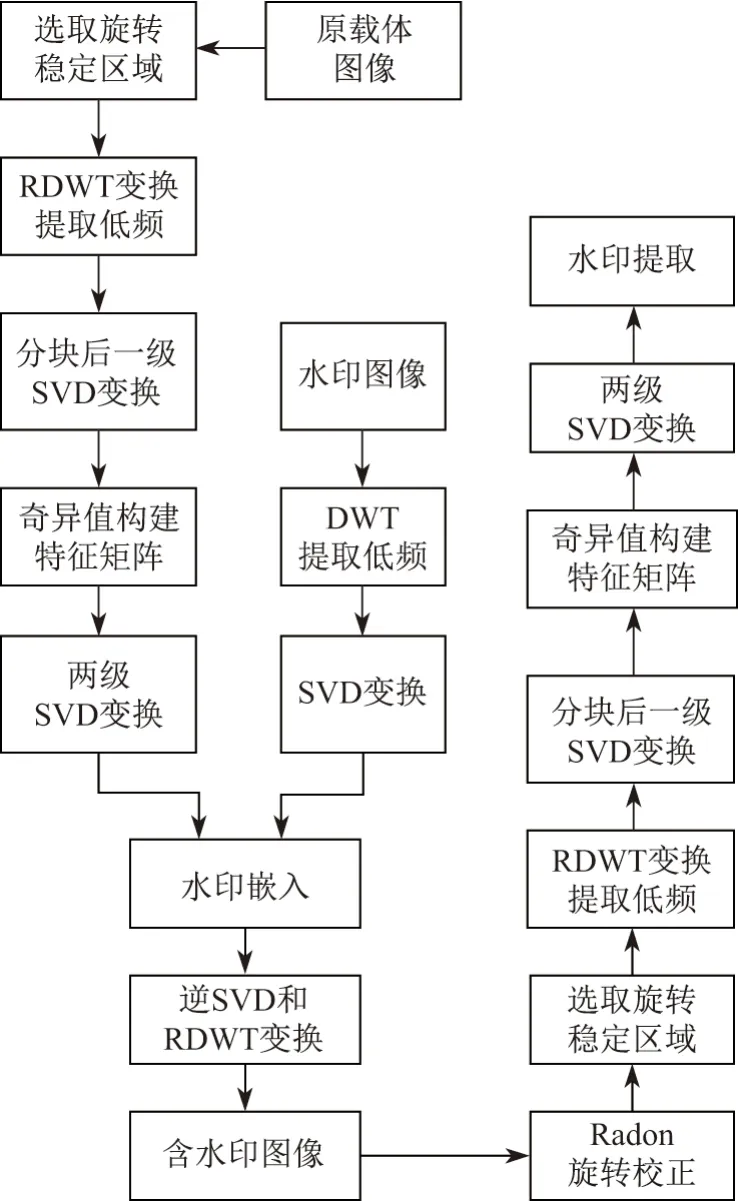
图4 水印嵌入与提取流程Figure 4 Watermark embedding and extracting process

2.2 水印的提取

水印的提取是水印嵌入算法的逆过程，两个过程基本相似.

步骤1将含水印的载体图像T∗进行Radon 旋转校正，得到图像

步骤2依据嵌入时保存的边长和左上角坐标选定含水印灰度图像的旋转稳定区域，其大小为M×M，对进行一层RDWT 变换，提取低频分量LL.

步骤3对低频分量LL 进行2.1 节中步骤3∼6 的操作，得到奇异值矩阵

步骤4根据嵌入时保存的矩阵O，经过SVD 分解得到奇异值矩阵S0，使用强度因子α计算出水印信息的奇异值

步骤5对水印信息的奇异值进行逆SVD 变换，得到含水印信息的图像

3 实验结果与性能分析

本实验的仿真搭建平台是MATLAB 2016a，实验中选取Lena、Baboon、Goldhil、Girl 为载体图像，大小均为512×512 像素，选取的稳定区域为256×256 像素，选取Camera 为水印图像，大小为64×64 像素.图5为4 幅测试图像(a)、(b)、(c)、(d)和水印图像(e).

3.1 不可见性测试

采用峰值信噪比（peak signal to noise ratio, PSNR）来判断含水印图像与原始图像之间的视觉相似性.水印不可见性、鲁棒性不可兼得，故应寻找最佳嵌入强度以取得两者之间的绝佳平衡.调整嵌入强度α，测试4 幅图像的不可见性，验证嵌入强度与不可见性的关系.表2为不同强度下对应水印图像的PSNR 值.

图5 原始宿主和水印图像Figure 5 Original host and watermark image

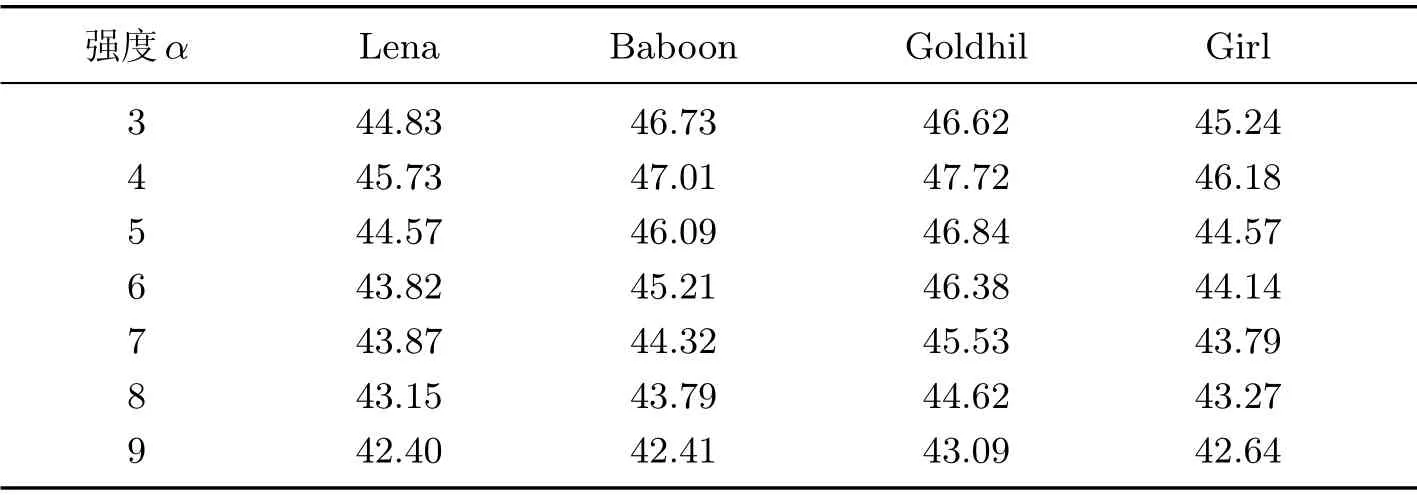
表2 不同强度下的PSNR 值Table 2 PSNR values of different intensities

当α为3∼4 时，PSNR 保持在45∼46 范围内，不可见性处于最佳状态；当α设置为5∼9 时，随着α的增大，PSNR 虽不断变小，但仍保持在40 以上.本文选取α=4 的嵌入强度，不可见性最好，PSNR 值可达到46.图6为嵌入水印后的图像和不受任何攻击下提取出的水印图像.

图6 水印嵌入和提取效果图Figure 6 Results of watermarking embedding and extraction

3.2 鲁棒性测试

对含水印的Lena 图像进行不同类型的攻击操作，并与文献[14]、文献[4]、文献[16]进行比较，如表3所示.从表3可以看出，增大攻击强度会影响一定水印清晰度，但仍能确切辨识出水印，其NC 值保持在0.950 以上.在缩放攻击时，因为缩小图像会导致部分像素丢失，而放大对图像像素信息是无损的，所以放大攻击后提取出的水印归一化相关系数（normalized correlation, NC）值稍高于缩小攻击.本文的NC 值比文献[14]的要高，虽然中值滤波的NC 值略低，但差别不大.另外，文献[4]和文献[16]均采用一级奇异值分解，本文采用的是两级奇异值分解，更好地保持了图像的稳定性特征，对常规几何攻击存在较强的鲁棒性.

表3 常规攻击NC 值对比Table 3 NC comparison of conventional attack

3.3 旋转攻击对比实验

目前水印的旋转攻击抵抗性比较差，文献[16]采用一级奇异值分解，且在水印提取之前没有进行校正；文献[11]把水印的S和V矩阵用作秘密密钥，将水印的奇异向量嵌入主图像的奇异值中；文献[15]先使用SIFT 变换对载体图像进行角度校正，然后进行水印提取.对含水印图像Lena、Baboon、Goldhil、Girl 进行10◦、30◦、50◦、70◦、90◦的旋转攻击，所提取的水印NC 值见表4.

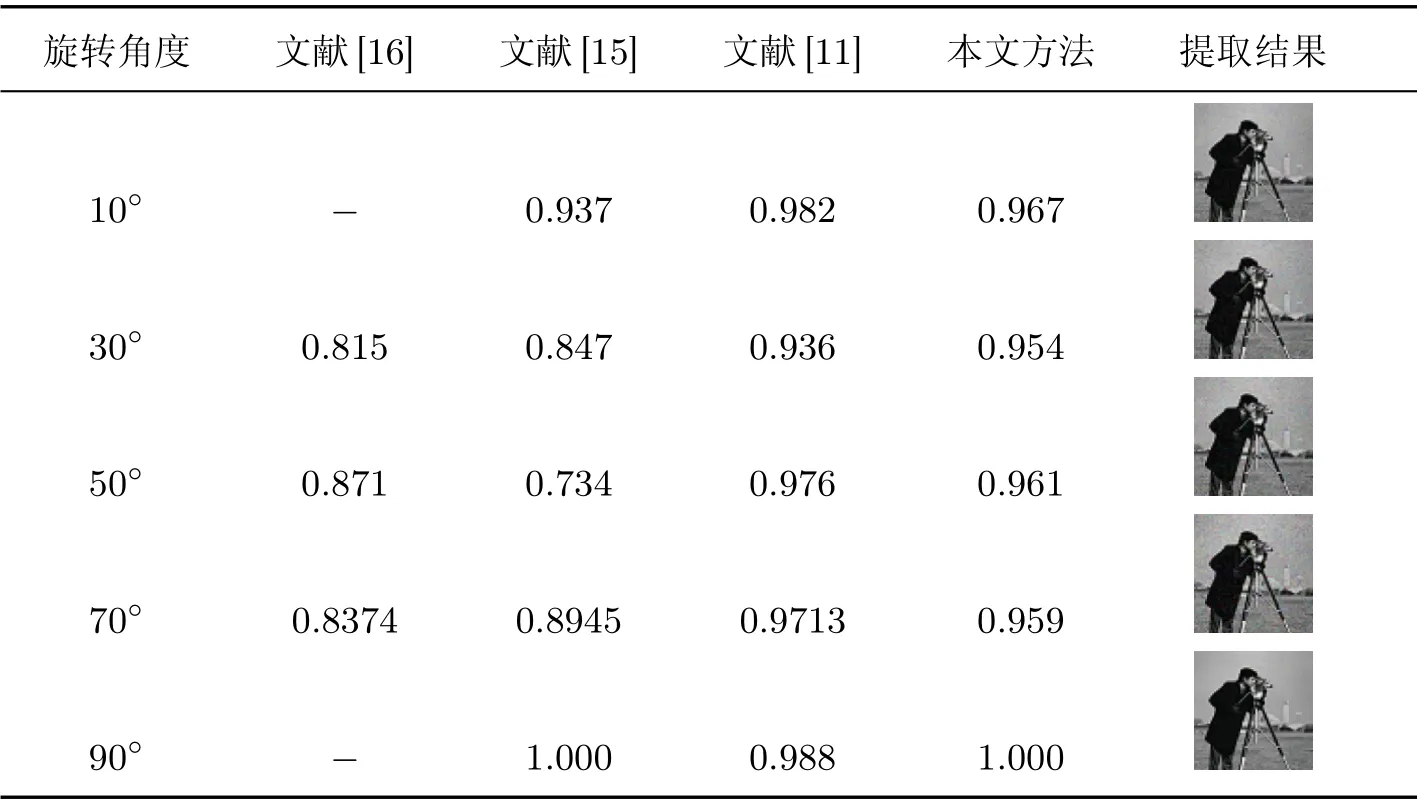
表4 旋转攻击实验及NC值对比测试结果Table 4 Rotational attack experiment and NC comparison test results

从表4可以看出，当含水印图像旋转一定角度时，提取的NC 值均在0.900 以上.当旋转90◦时，因为载体像素无任何损失，保持旋转稳定，所以提取的水印NC 值为1.000；对于30◦、50◦这两种中等程度的旋转，提取的水印信息的可辨性仍很高.本文算法采用了旋转稳定区域嵌入水印，且使用Radon 变换进行旋转角度的校正.在提取水印之前，先对含水印载体图像进行校正，且无需提取和匹配旋转前后图像的特征点.将水印信息嵌入载体的奇异值矩阵中，而奇异值具有旋转稳定不变性，能够有效抵抗旋转攻击.实验表明，本文算法能够有效抵抗旋转攻击.

4 结 语

为了平衡水印系统的不可见性和鲁棒性，解决抗旋转攻击能力较弱的问题，提出一种基于旋转稳定区域和两级奇异值分解的水印算法.将载体图像进行两级SVD 分解，使水印嵌入到第2 次SVD 分解后的奇异值矩阵中，对载体图像的破坏最小，而且也保证了算法的不可见性.选取旋转后像素值无损的稳定区域进行水印嵌入，并对旋转后的水印图像进行Radon 校正，从而提高水印算法的抗旋转攻击能力.理论分析和实验结果表明，在面对常规的几何攻击时，本文算法提取的水印NC值能达到0.90 以上，能保持较强的鲁棒性，具有一定的实用价值.