双时相影像联合不确定性对变化检测精度的影响机理探索

晁 剑，张慧芳，许长军，张鹏林

1.青海省地理空间信息技术与应用重点实验室，青海西宁810001

2.武汉大学遥感信息工程学院，湖北武汉430079

地壳运动（例如地震、火山喷发）、自然力量（例如沙漠化、气候异常、干旱、冰川移动等）和人类活动（例如人类的农、林、渔、牧、矿、工、商、交通、观光和各种工程建设活动等）都可能引起地表的变化.不断变化是地理实体、现象的基本特征之一[1].因此，对地表地理现象的变化检测已成为地球科学的重要研究方向之一，也是自然资源监测与管理、灾害监测、生态环境保护和可持续发展等领域的重要技术.可见变化检测在地理现象的动态监测中扮演着非常重要的角色.在地理现象的动态监测中，多时相遥感影像作为主要的数据源用于提取地表地理现象的变化信息，例如湖泊面积变化、森林砍伐、冰雪融化等.这就需要遥感影像变化检测能准确且可靠地探测真实世界地理现象中发生的变化，以满足地理现象动态监测的应用需求.然而文献[2]指出，不确定性存在于各种类型的影像、传感器和平台中，包括多光谱/高光谱影像、高空间分辨率影像和LiDAR 影像.这主要归因于混合像元、高精度地面控制点的缺乏、大气畸变与地面目标的模糊定义.因此，逐步发展起来的一些新兴技术正是通过评估、度量遥感影像的不确定性，进而抑制这些不确定性来提高遥感影像分析结果的精度.归纳起来，遥感影像不确定性研究成果可分为3 种情况：影像的不确定性度量、影像分析结果的不确定度量以及影像解译中的不确定性分析.

在影像的不确定性度量方面，文献[3]通过对高分辨率遥感影像地物光谱不确定性建模，提出了一种基于区间二型模糊集的且可用于超高分辨率影像的光谱不确定性建模方法.文献[4]研究了影像不确定性的量化度量模型，从空间分布的不确定性和语义的不确定性两个方面定义了遥感影像的不确定性度量指标和模型.

在影像分析结果的不确定性度量方面，文献[5]为了加深对影像固有不确定性的认识，开发了一种通用的数据建模方法，其中包含了对不同类型不确定性的建模；此外还提出了一种随机集方法用于从图像中提取空间目标进行不确定性建模.文献[6]分别对地理空间和特征空间的影像特征的不确定性进行建模和度量.文献[7]研究了多源遥感影像提取火烧迹地面积不确定性问题，以4 种国产卫星影像作为数据源，利用区分指数和确定度指数分析火烧迹地与林地在不同影像中的区分程度，并利用NDVI 多阈值和混合像元分解方法分别提取火烧迹地面积，旨在论证不同影像提取火烧迹地面积的差异.除此之外，文献[8-12]从不同的角度研究了遥感影像分类的不确定性分析和评价.

在影像解译过程中处理不确定性分析方面，文献[13]讨论了多源、多时相遥感影像高原湖泊提取过程的不确定性，包括遥感影像甄选、几何校正误差、数字化容差和目视解译经验等给提取结果带来的不确定性.文献[14]研究了影响面积估算模型性能的土地覆盖特征的不确定性来源.文献[15]在景观单元分类中通过包含与地表要素分类相关的不确定性提出了一种混合分类方法.该方法在超高空间分辨率多光谱卫星图像分类中包含了不确定性信息.文献[16]提出了一种集成不确定性分析的遥感影像尺度驱动变化检测方法，其结论表明该方法在提高变化检测精度方面优于一些当前的变化检测方法.

综上所述，目前有关遥感影像不确定性方面的研究主要聚焦于影像或影像分析结果的不确定性度量和评价，而很少研究影像的不确定性对影像分析和信息提取结果的作用机理.虽然文献[13-16]等在影像处理中考虑了不确定性因素，提高了影像处理结果的精度，但并未研究不确定性对精度的影响机理.另外，从目前的遥感影像变化检测研究成果来看，在影像的联合不确定性对变化检测结果精度影响方面的研究尚属空白.然而，只有探明联合不确定性与变化检测精度之间的关系，弄清影像联合不确定性对变化检测结果的影响机理，才能从根本上建立抑制这些不确定性的方法或模型，进而提高影像变化检测的精度.所以，本文以遥感影像变化检测为研究对象，通过分析影像的联合不确定性与变化检测结果精度之间的关系，探讨联合不确定性对变化检测精度的影响模式和影响机理.

1 研究方法

卫星传感器已广泛应用于地理现象的动态监测中.遥感影像不确定性的存在，要求研发具有鲁棒性的检测方法，且所获取的监测结果精度在可接受范围.因此，在遥感影像变化检测过程中，研究影像的不确定性对结果精度的作用机理是开发鲁棒的变化检测方法的关键.为此，本文提出基于地理统计学的思想以探明该机理，总体思路如图1所示.

图1 本文方法概览Figure 1 Overview of the proposed method

引起遥感影像不确定性的因素很多，例如传感器、天气条件、卫星姿态等，即使相同的传感器、相同的成像条件，因成像地理范围和地表覆盖物的差异性所引起的不确定性也不尽相同.为此，本文首先对输入的配准后双时相影像进行格网化，形成规则的格网单元作为计算单元，以反映不确定性的区域性差异.随后，按单元进行不确定性度量和变化检测，并进行变化检测精度的评价.一般认为输入影像的联合不确定性对变化检测结果的精度是相关的.为了进一步定量度量其相关性，首先基于地理统计学的相关性计算方法，研究变化检测中输入影像间的联合不确定性与精度的相关性.若具有强相关性则进一步探讨两者的关系；反之，如果两者弱相关或不相关，则表明联合不确定性对变化检测结果精度的影响有限.最后基于统计回归理论，以影像联合不确定性作为自变量来探讨变化检测结果精度的影响机理.

2 联合不确定性对精度的影响建模

2.1 数据准备

本文选用同一地理范围、时相间隔为1 个月、分辨率为1 m 的IKONS 影像作为建模数据，如图2(a)和2(b)所示.本文对输入的双时相影像采用200×200 像素的格网大小进行划分，两时相影像分别获得80 个单元格作为建模和检查单元，如图2(c)和2(d)所示.其中，64个单元格作为建模单元，16 个单元作为检查单元，用于检验模型的精度.建模单元与检查单元的分布如图3所示，其中红色填充单元为用于模型精度检查的单元，而其他单元则用于建模.然后，利用双时相变化检测算法对输入的双时相影像进行变化检测运算，以获取变化信息.本文采用了一种监督学习的支撑向量机算法进行变化信息检测，地面真值和变化检测结果如图4所示.

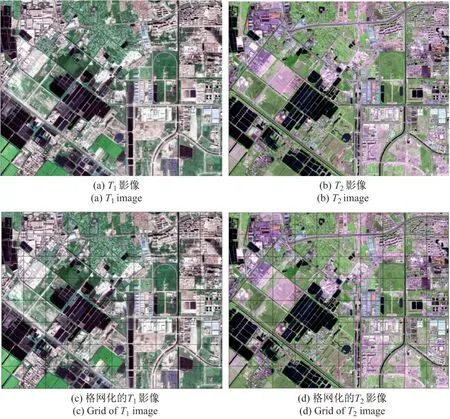
图2 双时相遥感影像及其格网化Figure 2 Bi-temporal remote sensing images and their grid

图3 建模单元与检查单元的分布Figure 3 Distribution of modeling units and checking units

2.2 联合不确定性与变化检测结果精度关系建模

根据图1的研究思路，双时相影像的联合不确定性对变化检测结果精度的影响机理包括联合不确定性度量、联合不确定性与变化检测结果精度的相关性评估、变化检测结果精度（因变量）与联合不确定性（自变量）之间的关系3 部分.

图4 地面真值及变化检测结果Figure 4 Ground truth and result of change detection

2.2.1 联合不确定性及其度量

影像联合不确定性是指参与变化检测的双时相影像之间存在的不确定性，在影像之间固有存在.本文采用归一化联合熵来对影像联合不确定性U进行度量.

式中，IT1和IT2分别为T1与T2时相的影像，p(xi yi)为参与变化检测的双时相影像的联合概率分布，i和j为像元位置的行列编号.

利用式(1)对图3所示的64 个建模单元的联合不确定性U分别进行度量，结果如图5中联合不确定性分布曲线所示.

2.2.2 联合不确定性与变化检测结果精度的相关性

为了探索变化检测结果精度与影像联合不确定性之间的关系，本文利用图4(a)所示的地面真值并以格网为单元来评价每个格网的变化检测精度，获取64 个建模单元的变化检测结果的精度值，结果如图5中精度分布曲线所示.

图5 建模单元精度与联合不确定性分布Figure 5 Distribution of accuracy and joint uncertainty of modeling units

图5从定性的角度反映了影像联合不确定性较高的单元，其变化检测结果精度却较低这一基本趋势.本文进一步利用相关系数计算了建模单元的影像联合不确定性与变化检测精度的相关性，有

式中，X为各单元联合不确定性构成的样本集，Y为各单元变化检测精度构成的样本集.根据式(2)可以得到两者的相关系数r=−0.602，这一结果表明两者之间呈现出比较强的负相关性.

2.2.3 变化检测结果精度与联合不确定性关系建模

为了解释影像联合不确定性和变化检测结果精度之间的关系，使用影像的联合不确定性作为解释变量X，分别利用线性回归和非线性回归拟合变化检测结果精度Y.图6所示为线性拟合的结果.

图6 变化检测结果精度与联合不确定性的回归Figure 6 Regression of change detection result accuracy and joint uncertainty

如图6(a)所示，利用统计线性回归方法可以建立联合不确定性X和变化检测结果精度Y之间的关系模型，公式为

在非线性回归方法中，本文分别采用指数法、对数法、二次、三次曲线进行建模，其中三次曲线的拟合精度最好，如图6(b)所示，模型公式为

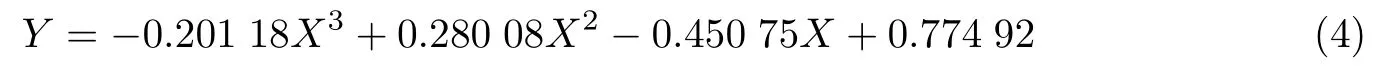
3 模型精度评估

为评估本文模型的精度，分别将建立的线性模型和三次模型应用于16 个检查单元（其分布如图3所示），对这些单元的变化检测精度进行预测，并计算预测结果与实际精度之间的残差和均方根误差，结果如表1所示.其中，残差1 表示一元线性模型预测精度与实际精度的残差，残差2 表示三次曲线模型预测精度与实际精度的残差.

从表1可以看出，有4 个单元的一元线性模型的预测精度与实际精度的残差大于等于0.1，而三次曲线模型的预测精度和实际精度之间的残差大于0.1 的就有3 个单元.从均方根误差来看，线性模型与三次曲线模型的结果非常接近.

4 结 论

不确定性是影像的固有特征，普遍存在于影像中.针对影像不确定性对变化检测结果的影响模式问题，本文基于空间统计学理论方法研究了双时相影像的联合不确定性与变化检测结果精度之间相关性的强度和方向，以及联合不确定性对变化检测结果精度的作用机制.可以得出以下结论：

1）双时相影像的联合不确定性与变化检测结果的精度之间呈现出强相关性，且方向为负.

2）从线性和三次曲线的回归线及精度评估结果来看，双时相影像的联合不确定性对变化检测结果的精度影响模式呈现出线性特征.

尽管本文研究为通过抑制不确定性的方法提高变化检测精度的工作奠定理论基础，但仅仅探索了双时相影像联合不确定性对变化检测结果总体精度的影响模式.今后的研究需要进一步探索影像的其他不确定性对变化检测结果精度的影响以及不确定性对变化检测结果的其他评估指标如Kappa 系数的作用模式等.