基于疯狂自适应鱼群算法的认知无线电频谱分配
2021-01-04苏慧慧曲文博
苏慧慧,彭 艺,曲文博
昆明理工大学信息工程与自动化学院,云南昆明650504
国际电信联盟(International Telecommunication Union, ITU)曾根据目前实际频谱需求的统计预测,2020年国际移动电信的需求约达2 000 MHz[1-3].全国各地频谱资源都面临匮乏问题,在德国、美国的一些区域,20~3 000 MHz 频段范围的频谱利用率不及50%;在新加坡的一些区域,80~5 850 MHz 的频谱利用率不及5%[2,4];据相关机构统计,中国许多频谱资源在时空上的平均利用率不到10%[3-4].充足的频谱资源是决定无线网络发展的关键因素之一,如何解决频谱短缺以及提高频谱利用率是目前无线通信方向的重要课题.频谱分配作为认知无线电技术的一个关键技术,其目的是将主用户未使用的空闲频谱进行合理分配,以实现频谱二次利用和最大化系统网络总效益[2].
目前,频谱分配模型主要有图论模型[5]、拍卖模型[6]、博弈论模型[7]等.图论模型通过选择不同的目标效用函数满足不同应用场景的需求.在固定拓扑下基于图论的频谱分配算法的优化目标主要有公平性最优、复杂度最优和系统传输效益最大化等.文献[8]首次将遗传算法[9]、粒子群算法[10]等智能优化算法应用于图论模型以解决频谱分配问题,并验证了算法的可行性.随后,免疫遗传算法[11]、人工蜂群算法[12]也被用于频谱分配的研究中,这些算法虽然在频谱利用率上进行了改进优化但是寻优精度不高.文献[2]是基于统计特性的蝙蝠算法对认知无线电频谱进行分配的研究,利用蝙蝠位置的统计特性进行网络效益的寻优,大大加快了算法的收敛速度,提高了算法的精度.目前,人工鱼群算法在频谱分配应用中的研究有限.文献[13]提出用人工鱼群算法与遗传算法融合的算法来弥补种群多样性差及精度不高的缺点,但融合过程增加了复杂度.文献[14]中将粒子群算法与人工鱼群算法结合,应用于水位流量关系中,精准度较高.然而,人工鱼群算法在全局搜索能力以及种群多样性的优化方面仍有很大改进空间,并且在认知无线电的频谱分配方面还有待提升.
人工鱼群算法虽然鲁棒性较强、收敛速度快,但若应用在频谱分配优化中时容易出现全局寻优能力弱、保持多样性差的问题,因此需要对其视野和步长参数进行自适应调整,在随机行为模式下引入疯狂算子,产生扰动以增加种群多样性.仿真实验表明,改进后的算法在全局寻优能力以及快速收敛等方面都有明显提升.
1 人工鱼群算法
1.1 基本人工鱼群算法
研究发现,营养物质较多的水域一般是鱼群聚集的位置,因此我们可以利用鱼群觅食过程来模拟实际应用中的寻优过程.人工鱼群的种群可用向量X=(x1,x2,···,xn)表示,种群当前状态用Xi表示,定义xi(i=1,···,n)为寻优变量;Y=f(X)为目标函数,即代表当前人工鱼群所处位置的食物浓度;dij为人工鱼xi与xj之间的距离;Fvisual为鱼群个体视野感知范围;Lstep为鱼群个体移动最大步长;ntry为鱼群个体在陷入局部最优时的最大尝试次数;next代表下一次迭代;δ为拥挤度因子[15].
1)觅食行为
在种群迭代中,每个人工鱼个体在其感知范围内随机选择状态Xj并求得此时刻食物浓度Yj.若Yj > Xi,则向Xj所在方向进行移动;否则在迭代中达到最大尝试次数后执行随机移动.用数学语言表示为
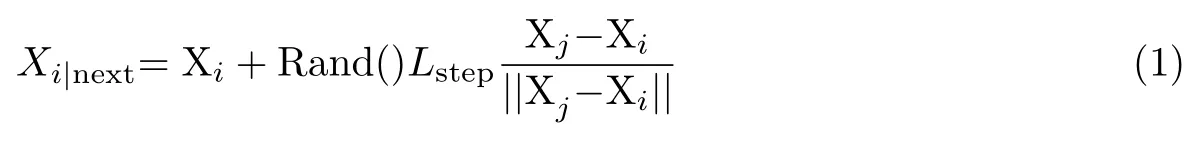
式中,Rand()是一个随机数,取值范围是[0,1].
2)群聚行为
在种群迭代中,每个人工鱼个体根据其视野感知范围内的其余个体数目n以及中心位置Xc进行探索,定义感知密度位Yc/n.若其大于δYi,执行群聚行为;否则执行觅食行为用数学语言表示为
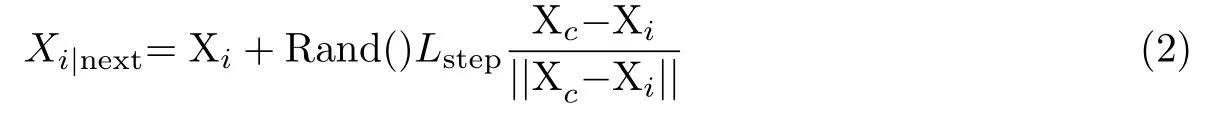
3)追尾行为
设人工鱼的当前状态为Xi,探索当前邻域内伙伴数的最大值Ymax的位置,若Ymax/n >δYi,说明Xmax处食物较多而且不太拥挤,否则执行觅食行为.用数学语言表示为

式中,Xmax为最优值状况下人工鱼群的状态,Ymax为人工鱼群中食物浓度的最优值.
4)随机行为
该行为是指在视野中随机选择一个状态并向其移动,避免出现局部极值.用数学语言表示为

5)公告板
用于记录在算法寻优过程中最优人工鱼个体的状态,即记录最优值.
1.2 改进后的人工鱼群算法
1.2.1 自适应视野和步长
传统人工鱼群算法定义视野范围Fvisual和步长Lstep为常数,两者决定了人工鱼群的寻优范围以及算法寻优精度.但算法在寻优过程的不同阶段对参数有不同要求,前期需要较强的全局搜索能力,后期需要严格的收敛精度[16].因此,定义上述参数为自适应调整参数
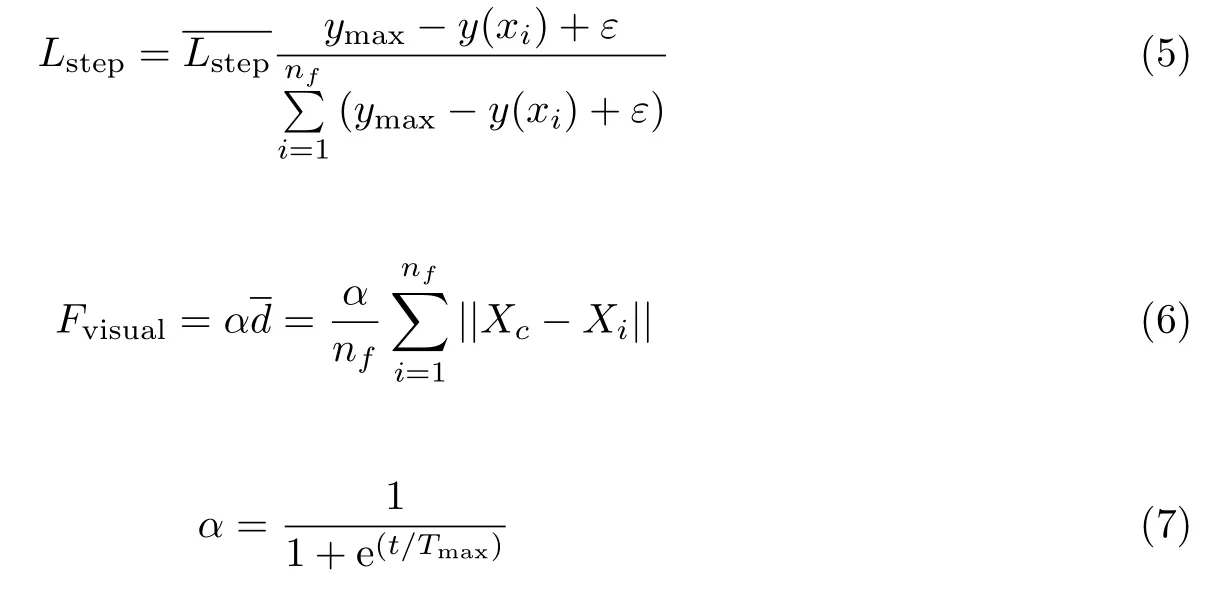
式中,t为当前迭代次数,Lstep为二进制编码的维数,Tmax为最大迭代次数,ε为机器精度(ε=10−6),ymax为最大适应度值,d为个体鱼到种群中心的平均距离.式(5)中的适应度值较大表示食物浓度较高,代表当前邻域内伙伴数目较多,则具有强大范围的探索能力.种群中每个人工鱼个体根据各自的适应度值进行移动来提高搜索精度;Logistic 函数是一种常见的S 曲线,可积分化简为

根据函数(8)的变化趋势可知式(6)中Fvisual值在前期区域值较大.引入S曲线可以提高算法的效率而避免出现局部最优,同时能调整视野变化以及人工鱼个体到鱼群中心的位置,保证了鱼群搜索的精度.
1.2.2 食物源引入疯狂算子
人工鱼群算法中食物源的位置是种群的寻优目的地.在设置最大迭代次数的行为运动中,种群多样性缺失也会造成局部最优现象.在人工鱼个体寻优移动过程中,如果食物源的中心位置陷入局部最优,那么种群范围内的搜索将会停止.因此,人工鱼个体采取行为移动时,引进了疯狂算子[17]来增加扰动,不仅避免了算法早熟收敛现象,而且人工鱼群在预先设定的疯狂概率下对食物源位置进行一定干扰,维持了个体多样性.当搜索完成后进行随机行为时,引入疯狂算子也可以使算法避免局部最优的问题.

式中,c1为[0,1]之间服从均匀分布的随机数;Pcr为预先设定的疯狂概率;xcraziness为一个较小值,此处取0.000 1.
2 基于人工鱼群算法的频谱分配
2.1 图论频谱分配模型
用户允许使用的频谱资源可以等效为色数.临近用户无权接入被占用的信道,为了避免产生干扰,被占用的信道得到释放后也不允许同类用户接入使用.于是把此种干扰情况等效为一条边,应用图论着色模型能很好地简化该问题,便于仿真研究.具体定义如下[5]:
1)在需要分配的认知无线电网络中,存在N个认知用户竞争M个频谱.
2)L={ln,m|ln,m ∈{0,1}}N×M表示空闲矩阵,其中ln,m=0表示用户n不可以使用m频谱.
3)效益矩阵B={bn,m}N×M表示认知用户n在使用频谱m的情况下所获得的效益.
4)干扰矩阵C={cn,k|cn,k={0,1}}N×N,cn,k=1表示用户n,k共同使用同一频谱所产生的干扰.
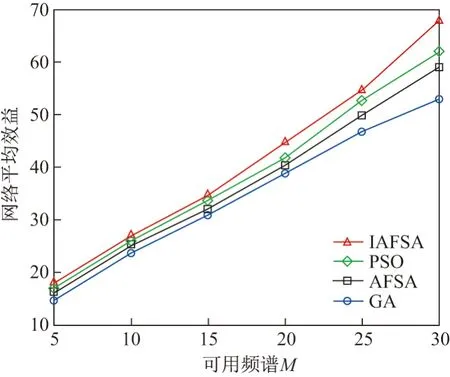
5)频谱分配矩阵A={an,m|an,m={0,1}}N×M,an,m=1表示频谱m分配给认知用户N.A满足的条件是:an,mak,m=0,且有cn,k=1,∀n,k 于是,每个认知用户所获得效益可表示为rn=an,mbn,m,其网络总效益的计算公式为 网络平均效益用UAMNE的计算公式为 在人工鱼群寻优过程中,与每次迭代人工鱼群的位置对应的均是一种频谱分配矩阵到二进制字符串的映射.在以网络总效益为目标函数的衡量下,选出最优值所对应的频谱分配矩阵A. 在图论频谱分配的模型下,改进算法后的频谱分配具体步骤如下: 步骤1初始化参数. 设置参数,包含可用频谱数M,认知用户数N,频谱可用矩阵L. 认知用户随机选择频谱数并生成在矩阵中的对应位置坐标,计算出效益矩阵B和干扰矩阵C,确定分配矩阵,目标函数为网络总效益. 步骤2初始化人工鱼群P(t),计算每个个体的初始网络效益,标记最大值ymax并传入公告栏. 步骤3根据干扰矩阵C进行无干扰约束处理,将种群与频谱矩阵A中的元素进行一一映射. 步骤4记录每次鱼群迭代的个体的网络效益最优值及其相应个体. 步骤5根据视野范围Fvisual和拥挤度因子确定鱼群执行行为类型;比较不同行为的网络效益值从而确定聚群、追尾或觅食操作,以更新人工鱼位置信息. 步骤6与公告板进行比较,获取优良人工鱼个体,更新网络效益最优值. 步骤7查看终止判决条件,若符合条件则输出最优值,否则返回步骤5. 公告板值即为网络效益最优值. 为了验证本次改进在频谱分配应用中的可行性,在Matlab 软件平台上建立仿真环境,并将其与遗传算法、粒子群算法以及未改进的人工鱼群算法的频谱分配进行目标函数对比,此外还对可用频谱M和认知用户数N进行了变量控制分析. 采用不同算法进行相同的频谱分配验证时,将涉及到的频谱矩阵(可用矩阵L、效益矩阵B、干扰矩阵C)与算法前后保持一致.在实验过程中,假设认知无线网络中的用户是无噪和静态的.粒子群算法中的参数设置参考文献[8],遗传算法中的参数设置参考文献[18],最大迭代次数Tmax=200 ,机器精度ε=10−6,nf=20,拥挤度因子[13]δ=0.618,尝试次数ntry=10,疯狂概率Pcr=0.3,xcraziness=0.000 1. 在相同的认知无线网环境下,采用粒子群算法、遗传算法、人工鱼群算法和改进后的人工鱼群算法进行频谱分配,其网络总效益的对比曲线如图1所示,实验中M和N均设置为定值15.从图1中可以看出,4 种算法的的网络总效益都随着迭代次数的增加而增加,直至接近最大值. 图1 不同算法的网络效益值对比图Figure 1 Comparison of network benefits by different algorithms 从图1中发现:当迭代次数为80 时,改进后的人工鱼群算法已经逐渐趋于全局最优,相比于其他3 种算法,其收敛速度占有明显优势;改进后的人工鱼群算法在前80 次迭代时具有良好的全局搜索能力,与遗传算法相比,本次算法的改进在网络总效益值方面还是取得了较好的效果,使最优解的挖掘能力也得到了提高. 图2和3 分别描述了M和N变化时网络平均效益的变化曲线.从图2可以看出,当N为20 时,网络平均效益随着M的递增呈现明显递增趋势;当M较小时,4 种算法之间的差距并不大;当M25 时,其差距明显变大,由此可以体现出本文方法的有效性.由仿真图2可知:当前期M较小时,认知用户之间对于频谱的竞争性较大,因此网络效益值较低;在算法后期当M增加时,干扰冲突减小,系统负荷也在减轻,因此后期网络平均效益增长较快. 图2 可用频谱M 变化下的网络平均效益Figure 2 Average benefit of network under change of available spectrum M 图3 认知用户N 变化下的网络平均效益Figure 3 Average benefit of network under change of cognitive user N 由图3可以看出,在M为20 的仿真对比试验中,当认知用户N不断增加时,用户的通信质量会受到一定影响,所以网络平均效益随着N的递增呈现明显递减趋势,可见改进后的算法与其他算法相比差异并不显著.当N在[10, 25]区间时,本文算法的目标函数值最大,下降梯度最小.可以看出在网络负载增大时,本文所改进算法的系统性能相比于其他粒子群算法、遗传算法、人工鱼群算法,影响最小且鲁棒性较强. 对目前人工鱼群算法存在的问题进行改进并将其应用于图论的认知无线电频谱分配模型中.对该算法中的视野和步长进行自适应调整,并在人工鱼个体觅食过程中执行随机行为时引入疯狂算子以增加种群多样性.研究表明:与其他遗传算法相比,本文所提的改进算法在频谱分配模型寻优时的全局搜索能力更强,不但能避免过早收敛而导致的搜索结果不佳问题,而且增加了种群多样性并提高了最优解精度.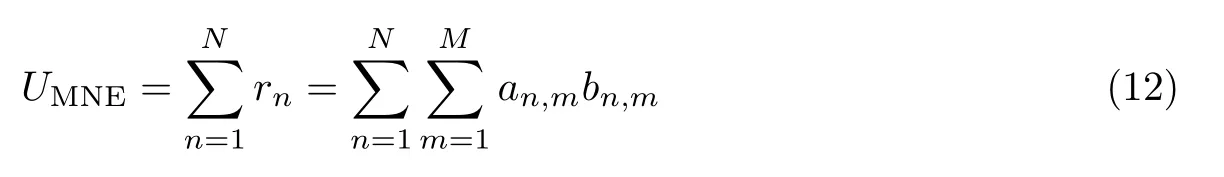

2.2 基于疯狂自适应人工鱼群算法的频谱分配描述
3 仿真实验及结果分析
3.1 不同智能算法的网络效益值对比

3.2 可用频谱M 和认知用户N 对网络效益值的影响

4 结 语
