基于异类类内超平面的模糊支持向量机及其应用

陈继强，余志鹏，张 峰，张丽娜

(河北工程大学 数理科学与工程学院，河北 邯郸 056038)

个人信用评估是指银行等金融机构通过对影响借贷人还款的各种主客观条件环境的综合考察，运用严谨的科学方法评估借贷人的借贷信用及其还款能力，从而对借贷人是否具有履行偿还银行等金融机构的借贷能力进行评估，本质上是一个不平衡数据集的二分类问题。然而，我国的信征体系发展较晚，个人信用评估模型的研究尚不完善，亟需进行深入研究。

专家评分模型[1]是最早被应用于个人信用评估的模型，但是由于其评估结果易受主观因素干扰等问题，逐渐被舍弃。后来，Carter& Catlett[2]将Fisher判别分析运用到个人信用评估领域，Orgler[3]利用线性回归分析方法建立了个人信用评估模型，都取得了一定的成果。然而，这种基于统计学的方法难以处理信贷数据集中的噪声数据。后来，随着机器学习理论的发展，一些学者将决策树与支持向量机等机器学习算法应用于信贷评估[4-12]，均取得较好的效果。但是，这类方法在处理不平衡信贷数据集时的分类能力是有限的。随着科学技术水平的发展，一些学者致力于集成模型在个人信用评估领域中的应用研究。例如，丁岚骆等[13]构建了Stacking集成策略的借贷人违约风险评估模型。夏国斌[14]将基于Bagging集成法的集成支持向量机模型运用于个人信用评估中，饶希[15]将基于Boosting集成法的逻辑回归与支持向量的集成模型运用于个人信用评估中。郭孝敬[16]运用了基于逻辑回归与决策树的集成模型，王思懿[17]将随机森林与逻辑回归的集成模型运用到个人信用评估中，张碧月[18]实验结果表明RF-APSOLSSVM的预测精度比RF模型和APSOLSSVM模型的精度高。王黎等[19]的实验结果表明GBDT模型明显优于支持向量机和逻辑回归的效果。赵天傲等[20]将XGBoost算法应用在个人信用风评估中，与决策树、支持向量机等模型进行对比分析，实证结果表明XGBoost模型比单一模型的预测精度提升效果比较明显。虽然集成模型分类效果相对于其单一模型分类效果较好，但是它们同单一模型一样也没有考虑不平衡信贷数据集中噪声数据对于分类结果的影响。

综上所述，当前关于个人信用评估问题的研究，现有方法没有很好地处理不平衡信贷数据集中噪声对模型分类精度的影响。因此，为了降低噪声数据对模型分类精度的影响，本文考虑了不同样本在分类问题中的不同作用，构建了一种基于异类类内超平面的模糊支持向量机，为信贷评估问题提供了一种新方法。

1 支持向量机简介

支持向量机是20世纪90年代中期由Cortes和Vapink提出的一种有监督的学习方法。其基本思想是通过最大化间隔寻找最优分类超平面，从而对数据进行分类，自提出以来被广泛应用[21-23]。

为不失一般性，这里以二分类问题为例。假设给定的训练集为

T={(x1,y1),…,(xn,yn)}

(1)

其中xi∈Rm,yi∈{-1,+1}为类标签，i=1,2,…,n。对于非线性分类问题，通过映射φ(x),将训练数据集从原空间映射到高维特征空间，使得映射后的数据集在特征空间中线性可分。因此，支持向量机的学习问题可用如下二次规划问题来描述：

s.tyi(ω·φ(xi)+b)≥1-ξi

ξi≥0,i=1,2,…,n

(2)

其中‖·‖表示向量的模，C>0为惩罚参数，ξi为松弛变量。原问题(2)的求解可通过构造拉格朗日函数，转化为如下对偶问题来求解：

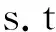
0≤αi≤C，i=1,2,…,n(3)

问题(3)中K(xi,xj)=(φ(xi),φ(xj))为核函数，αi为拉格朗日乘子。

通过求解对偶问题(3)可得分类函数为

进一步可得决策函数为

f(x)=sgn(g(x))

这样，对于新的样本x′,其预测类别为f(x′)。

2 基于异类类内超平面距离的隶属函数

隶属函数是模糊数学中的一个重要内容，可用于为不同样本设定不同的权重[24-27]。本文考虑到在支持向量机中对确定最优分类超平面起决定性作用的只有支持向量，而支持向量的位置一般又位于距离异类点较近的区域。为此将模糊理论引入支持向量机中，设计了基于异类类内超平面距离的隶属函数。该方法的思想是根据每个向量到异类类内超平面距离的不同，将样本输入xi到异类类内平面距离的函数作为隶属函数，对训练集中的输入xi赋予相应的权重(隶属度)来提高支持向量在训练样本中的作用。

如图1所示，对于训练样本集{(x1,y1),(x2,y2),…,(xn,yn)},假设正类样本(在图中用菱形表示)数目为n1，负类样本(在图中用圆形表示)数目为n2,n1+n2=n。在线性不可分时，通过映射φ(x),将数据集从样本空间映射到特征空间，数据集变为{(φ(x1),y1),(φ(x2),y2),…,(φ(xn),yn)}。

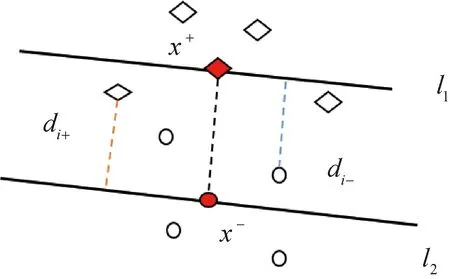
图1 基于异类类内超平面的距离示意图Fig.1 Diagram for the distance of heterogeneous hyperplane

因此，正类样本点xi到负类类内超平面l2的距离可定义为

(4)

同理，负类样本点xi到正类类内超平面l1的距离可定义为

(5)

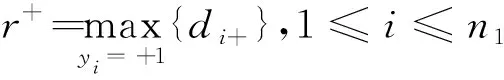
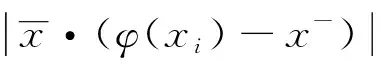
=|(x+-x-)·(φ(xi)-x-)|

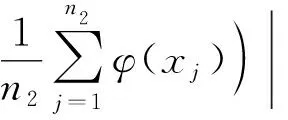
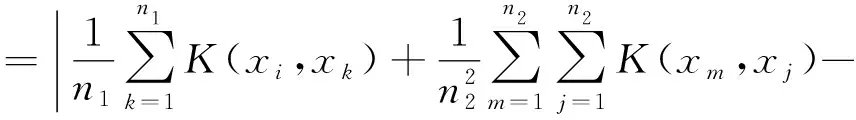
同理，当yi=-1时，di-的分子及r-可分别表示为

这样，为了表示第i个样本隶属于对应类标签的程度，可设计如下基于样本点到异类类内超平面距离的隶属函数

(6)

式(6)中σ是一个给定的很小的正数，目的是为了保证隶属函数μi的取值大于0。

3 基于异类类内超平面的模糊支持向量机

传统的支持向量机是把所有的训练样本看作同等重要的，这使得获得的分类超平面对噪声数据或者非支持向量样本较为敏感，从而导致获得的最优分类超平面存在偏差，进而影响分类器的分类精度。为了克服上述问题，本小节将上节设计的隶属函数赋予每个向量不同的权重，并结合传统支持向量机，构建基于异类类内超平面的模糊支持向量机。

在引入隶属函数μi后，训练样本集{φ(xi),yi}变为{φ(xi),yi,μi}其中0≤ui≤1,i=1,2,…,n,它表示第i个样本隶属于对应类标签的程度。这样，可建立如下二次规划问题：

s.tyi(ω·φ(xi)+b)≥1-ξi

ξi≥0,i=1,2,…,n

(7)

其中C>0为惩罚参数，μi为式(6)给出的隶属函数，ξi为松弛变量。对于原问题(7)，通过构造拉格朗日函数，可转化为如下对偶问题：

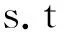
0≤αi≤μiC,i=1,2,…,n

(8)

其中K(xi,xj)=(φ(xi),φ(xj))为核函数，αi为拉格朗日乘子。结合传统支持向量机，可设计求解上述优化问题的求解算法，该算法就称为基于异类类内超平面的模糊支持向量机。

下面将通过UCI数据集和信用评估问题的实验验证所设计算法的有效性。

4 实验

UCI数据库是加州大学欧文分校(University of CaliforniaIrvine)开发的用于机器学习的数据库，UCI数据集是众多学者常用的标准测试数据集。为了验证上述构建的基于异类类内超平面的模糊支持向量机的有效性，本节将首先利用UCI数据集选择部分数据进行实验，然后在个人信用评估问题中验证该方法的有效性。

4.1 模型评估指标

考虑到数据集的不平衡性，选取F1值。F1是非平衡数据集分类问题中有效的评价准则之一[28]，它是基于混淆矩阵的一个评估指标，详见式(9)。

在分类任务中，混淆矩阵是一个N×N的矩阵，其中N是被预测的类别数，在本文中由于是一个二分类任务，所以混淆矩阵是一个2×2的矩阵。表1是一个二分类任务中的混淆矩阵实例表。

表1 基于二分类的混淆矩阵

F1的计算表达式为[25]

(9)

4.2 基于UCI数据集的实验

本小节选取UCI数据库中4个不同的数据集进行实验，各数据集的样本数量、属性数量、正负类样本数量详见表2。

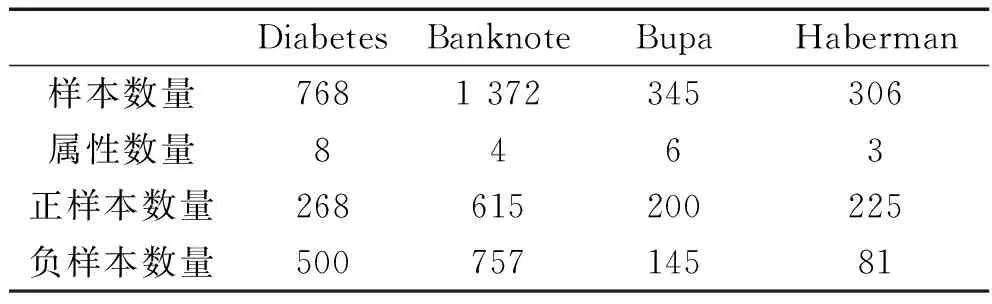
表2 数据集描述

为了验证本文提出的基于异类超平面的模糊支持向量机(DHFSVM)的有效性，将它与传统的支持向量机(SVM)、决策树(DTC)、高斯朴素贝叶斯模型(GNB)三种模型分别在4种UCI数据集上进行实验，实验结果如图2所示。

从图2中可以看出，DHFSVM算法在Bupa、Diabetes、Habeman等3个数据集上的F1值为最高，在Banknote数据集上为第二高。这说明，本文所构建的DHFSVM算法考虑了不平衡数据集中不同样本在分类过程中的不同作用，有效地提高了不平衡数据分类的准确性。

图2 基于GNB、SVM、DTC与DHFSVM在数据集上的F1值柱状图Fig.2 Histogram of F1value with GNB,SVM,DTC and DHFSVM

4.3 个人信用评估中的应用

在个人信用评估问题中，信贷数据涉及到个人隐私等问题，众多信贷数据无法开放获取，因此本文中采用来自Kaggle数据科学竞赛平台上的信贷数据集，该数据集的名称为“Give Me Some Credit”。在该数据集中，包含10个解释变量xi,i=1,2,…,10,一个被解释变量y。具体如表3所示。

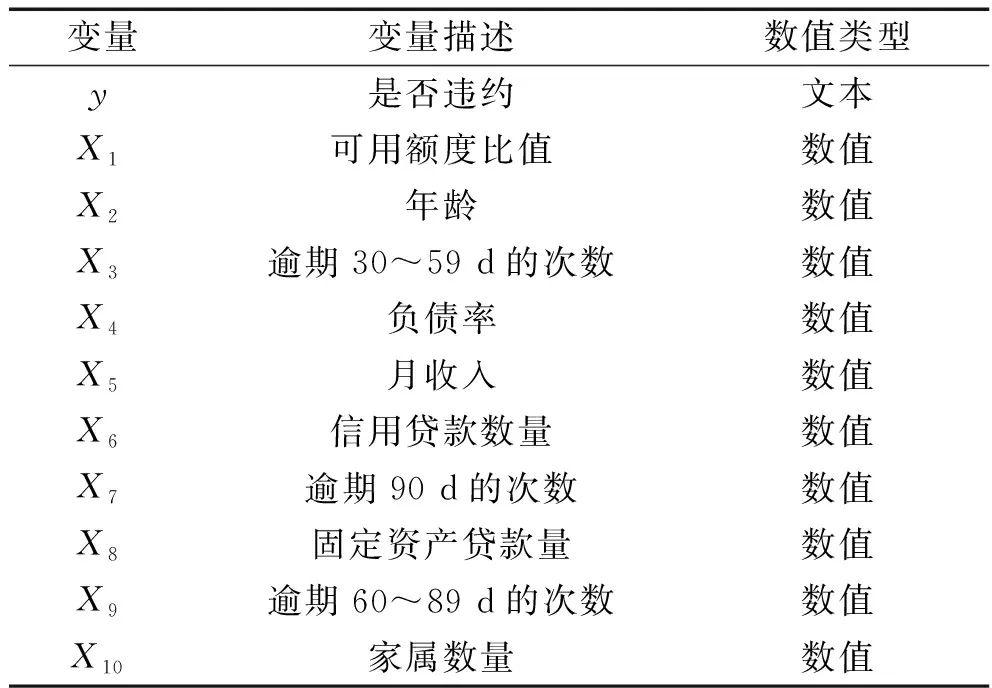
表3 变量及其描述

由于该数据集数量较大(将近15万条)，本实验随机选取了其中的1 000条数据，其中违约数据为200条，未违约数据为800条。在图3中，给出了GNB、SVM、DTC以及DHFSVM基于“Give Me Some Credit”数据集的分类混淆矩阵。

由式(9)F1值及如图3所示的混淆矩阵可以计算得出各个模型对应的F1值，结果如图4所示。

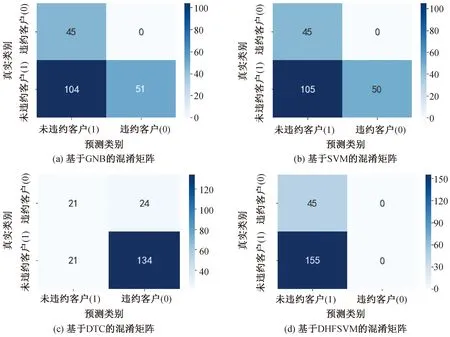
图3 基于GNB、SVM、DTC和DHFSVM的混淆矩阵Fig.3 Confusion matrices with GNB,SVM,DTC and DHFSVM

由图4所示的结果可以看出，在GNB、SVM、DTC和DHFSVM 4种算法中，本文所构建的DHFSVM算法表现最好，取得了最大的F1值0.87。这说明，在分类算法的构建时，充分考虑不平衡数据中不同样本点(包含噪声)所起的不同作用，可有效提高分类算法的精度，也说明了本文所构建的DHFSVM算法可以较好地应用于个人信用评估问题。

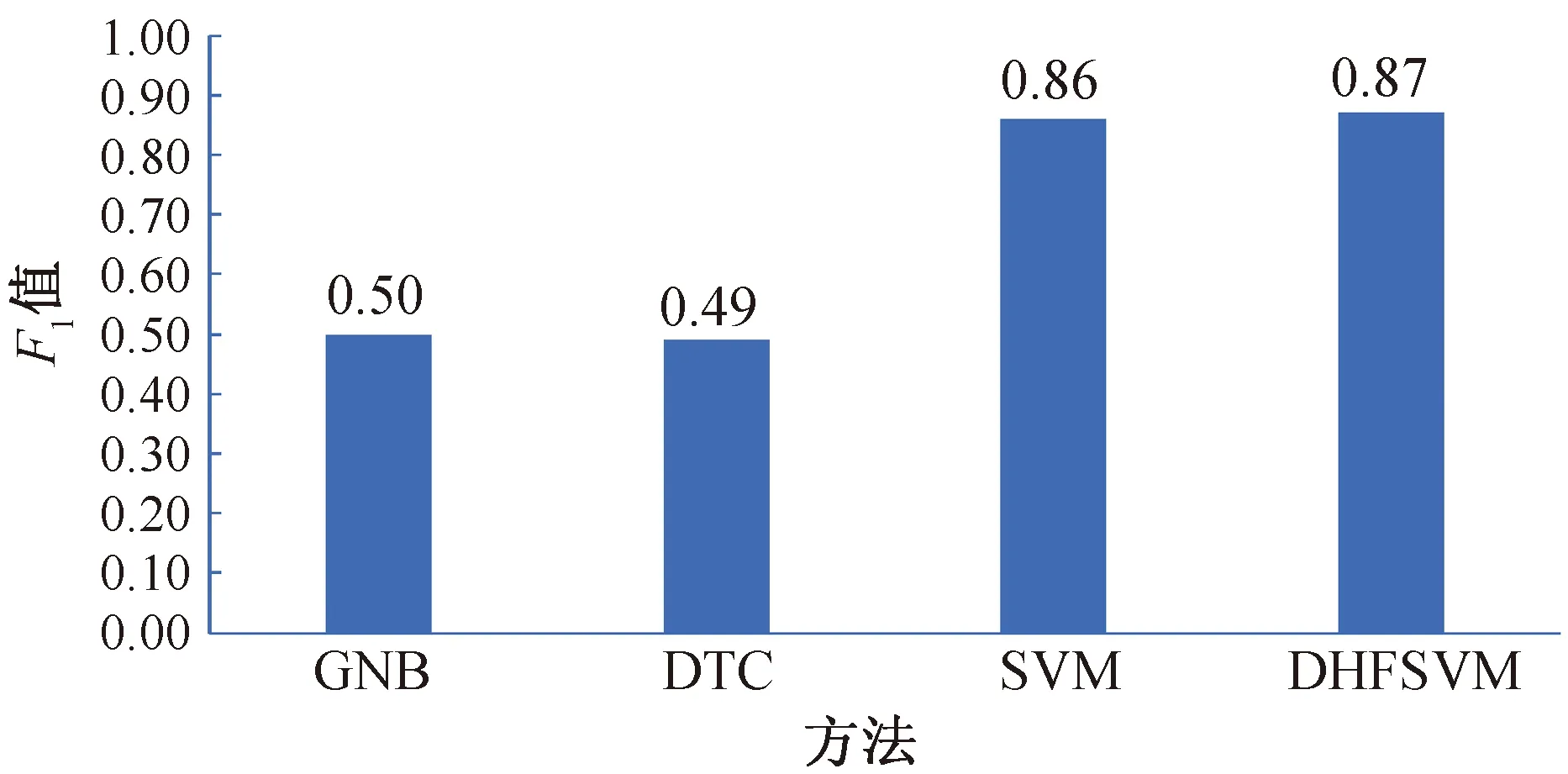
图4 基于GNB、SVM、DTC与DHFSVM在信贷数据集上的F1值柱状图Fig.4 Histogram of F1 value on the credit data with GNB,SVM,DTC and DHFSVM

5 结论

本文结合模糊数学理论、经典支持向量机，构建了一种基于异类类内超平面的模糊支持向量机(DHFSVM)。与GNB、DTC、SVM 3种方法对比发现：(1)DHFSVM算法在Bupa、Diabetes、Habeman等3个数据集上的F1值最高，在Banknote数据集上第二高，表明所构建的DHFSVM算法可通过赋予不同样本不同的权重来降低噪声对风险评估带来的影响；(2)在Kaggle数据科学竞赛平台上提供的真实信贷数据集进行的实验发现，DHFSVM算法表现最好，取得了最大的F1值。表明DHFSVM算法可有效提高不平衡信贷数据集的分类准确性，可为个人贷款业务中个人信用风险评估问题提供借鉴。