基于组合模型的城市轨道交通全线客流预测分析

文晶琳　钟梦娟　吴文谦

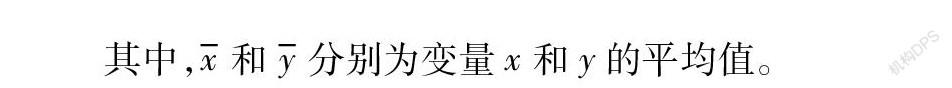
摘要：为合理组织城市轨道交通系统客流，提升城市轨道交通使用效率，本文将基于组合模型，对城市轨道交通全线的客流预测进行分析。通过剖析城市轨道交通客流的影响因素后，基于相关性分析，研究客流与其影响因素的相关度;再基于时间序列及差分的方法，对原始客流数据平稳化处理;最后基于ARIMA模型进行客流预测并检验数据结果，以得出更符合未来实际发展的全线客流数据。

关键词：城市轨道交通：全线客流預测：组合模型

凭借着安全系数高、运行速度快、不易受天气影响等优点，轨道交通逐渐成为大部分出行者的选择。但总体上依然很难满足快速增长的客流需要，需要准确预测客流量信息，规划列车运行方案，合理组织客流。

客流预测拥有较广阔的前景，国内许多学者已经进行了多方面的分析研究，借助方法和建立模型以获得成果。林璐通过相关回归法，解析相关影响因素，再拟合ARIMAX模型进行预测，得出该模型预测效果更好，有实际应用价值的结论;闻克宇等人提出一种短期客流预测方法，通过改进迁移学习得到，再将某铁路局客票数据作为研究案例预测，以更好地提升资源配置效率与客货运服务水平。于颢晨基于四阶段法，针对客流预测中风险指标，分析结果敏感性后，预测沈阳市轨道交通线路客流。

本文基于组合模型，针对城市轨道交通线路，进行月均客流量预测。首先，通过分析客流形成机理及影响因素。借助相关性分析，得出与客流变化有关的影响因素，将其作为研究变量。其次，基于差分和季节性差分的方法，对初始客流数据作平稳化处理，合理化时间序列图。再次，基于ARIMA模型，比较各类模型的相关统计量及拟合值检验数据结果，再对模型进行修改。最后，基于构建的组合模型，以深圳地铁7号线为例，进行客流预测研究。经过不断优化，得到更合适该线的预测模型类型，以及更具针对性、更符合未来发展的客流预测数据。

1城市轨道交通客流分析

1.1客流形成机理

城市轨道交通客流，是指当人们乘坐轨道交通时，在一定的时间及空间范围内有目的地移动，单位时间内人数及移动的总和。主要由基本客流、诱增客流和转移客流三部分组成。基本客流是指在城市轨道交通初期建设时，要求拥有的客流数量，以达到城市轨道交通的建设必要性。诱增客流是指由于新建的城市轨道交通促进其他居民对此的出行行为而增加的客流。转移客流是指由于城市轨道交通运营吸引其他交通方式中的部分客流量转移到该线。

1.2客流影响因素分析

城市轨道交通客流受众多因素影响，对其做出分析，为后续城市轨道交通的建设及相关客流预测做铺垫参考。影客流因素主要包含以下几点：

（1）沿线土地利用。沿线土地利用决定了未来城市发展的情况，能够带动沿线商业发展，促进沿线人流量的增长与市内就业率的增长。同样，线路周边土地的开发利用程度都决定了客流量的大小、出行时间及去向。比如，若车站周边是大型商场、旅游景点等，那么在节假日时客流数额也将非常庞大。

（2）经济水平。城市经济水平，也就是政府的财政能力，都会直接影响着是否可以支付相关建设运营资金。一般来说，当城市的经济发展水平较高、政府财政水平合理时，才能有足够的资金投入。除此之外，还能根据实际情况、市民的承受能力制定出合理票价，提高居民的出行意愿，进一步扩大线路客流量。

（3）服务水平。服务水平的影响因素包括车辆票价、运营配置和乘车环境舒适度等。通过以往对城市轨道交通研究表明，票价变化、设施服务对客流量都会有很大的影响，当降低车辆票价，有可能会吸引到更多的客流量出现。另外，对发车间隔、运营时刻表等进行合理配置，提高服务水平，可以对客流量产生积极影响。

2组合模型的构建

2.1相关性分析

为研究两个变量间的相关关系密切程度，我们最常使用的分析方法是Person，分析法。基于相关分析，可以研究各类影响因素与客流量之间的相关关系，从而确定后续时间序列模型的建立。

相关系数是衡量两个变量之间线性相关强度的量，通常用字母r表示。最常用的是皮尔逊相关系数，其公式如下：

当0≤|r|<0.3时，两个变量之间被认为不存在相关性;当0.3≤|r|<0.5时，变量间存在低相关;当0.5≤|r|<0.8时，变量间存在中度相关;当0.8≤|r|<1时，变量间存在高相关。

2.2时间序列平稳化检验及平稳化处理

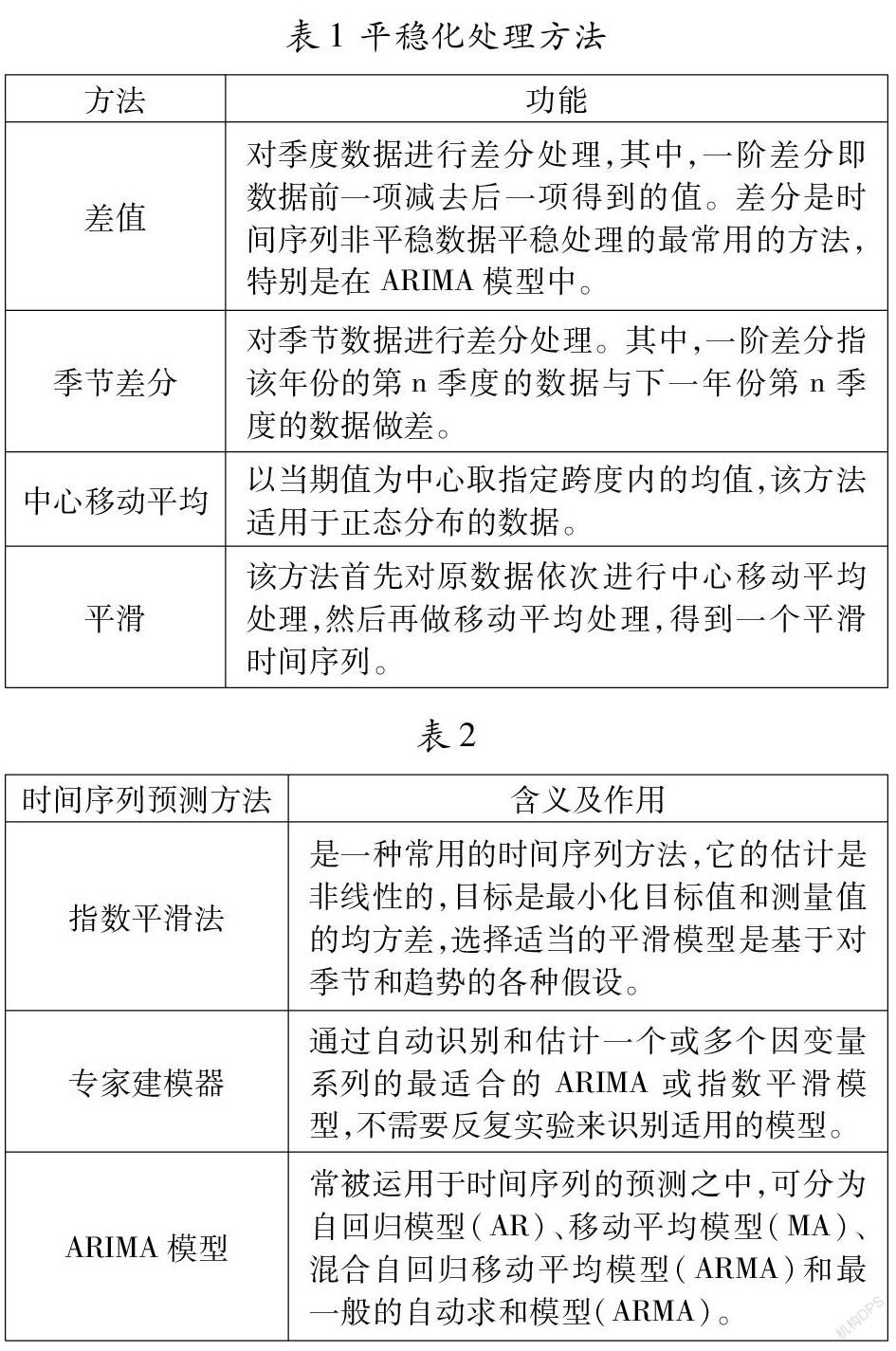
在进行客流预测前，往往需要对历史客流数据进行平稳化检验。时间序列存在非平稳性，需要通过差分处理，并再次进行平稳性检验，直至平稳为止，差分的阶数为模型ARIMA（p，d，q）中d的数值，平稳化处理的方法如表1所示。

2.3模型识别

在spss统计分析软件中，时间序列预测方法大致被分为有三种，在本文研究中，由于影响客流数据的因素较多，我们将直接利用SPSS软件中的专家建模器（仅限ARIMA模型），以建立合适的时间序列预测模型，相对其他方法，此法较为简便且模型适合度更高。如表2：

2.4模型定阶及参数估计

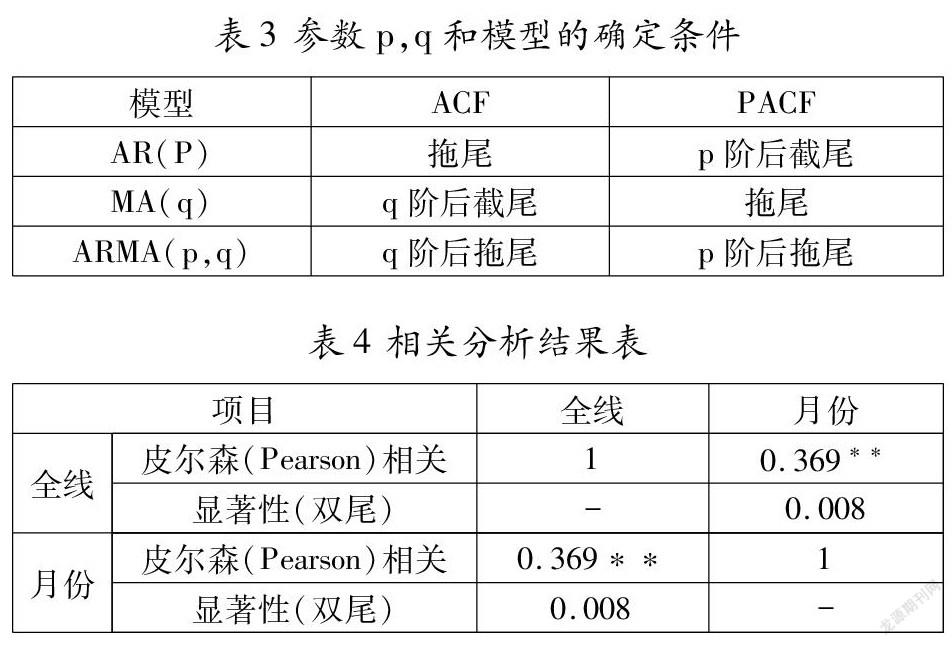
ARIMA（p，d，q）模型通过分析得到的自相关图（ACF）和偏相关图（PACF），分别对平稳序列进行ACF和PACF图分析，综合差分阶数，得到最佳参数p，q和d。将时间序列作自相关图进行平稳检验后，分别观察ACF图与PACF图的截尾性，二者不是拖尾就是截尾，否则判断为非平稳序列。非平稳序列在差分后继续进行平稳性检验，直至满足平稳性条件，则d值确定，参数p、q及模型的确定方式如表3所示。

2.5模型检验

ARIMA模型的验证主要是验证其拟合效果，若时间序列的变化特征可以基本被模型所解释，那么模型的噪声序列则为白噪声序列。具体的检验方法可利用Barlett法检验统计量Q。若求得的模型不能通过检验，那么应该重新拟合模型，直至模型能通过白噪声检验为止。

3预测实例分析

3.1深圳地铁7号线概况

深圳地铁7号线以南山区西丽湖站作为起止点，到罗湖区太安站结束。每天的客运流量、车厢拥挤的程度都在不断发生变化，将面临日常运营、应急组织等艰巨挑战。在这些情况下，提前做好客流预测研究分析显得尤为重要。基于历史客流数据建模将更加具有准确性和可靠性，本文将以该线2016年10月至2020年12月的每月全线的平均客流量作为原始数据，对其进行客流预测研究。

3.2双变量相关性分析

通过研究其全线月均客流量与时间之间的相关关系密切程度，可以验证实验数据的准确性。再利用SPSS软件进行相关性分析，得到表4的分析结果。从表中可以看出，两个变量之间的相关系数为0.369，为正相关，且具有较强的相关性。同时两者之间的显著性水平为0.008，低于0.01，差异性非常显著。由此可以得出，此历史客流数据在预测未来年客流量趋势上具有比较强的可靠性。

3.3原始客流量时间序列预处理

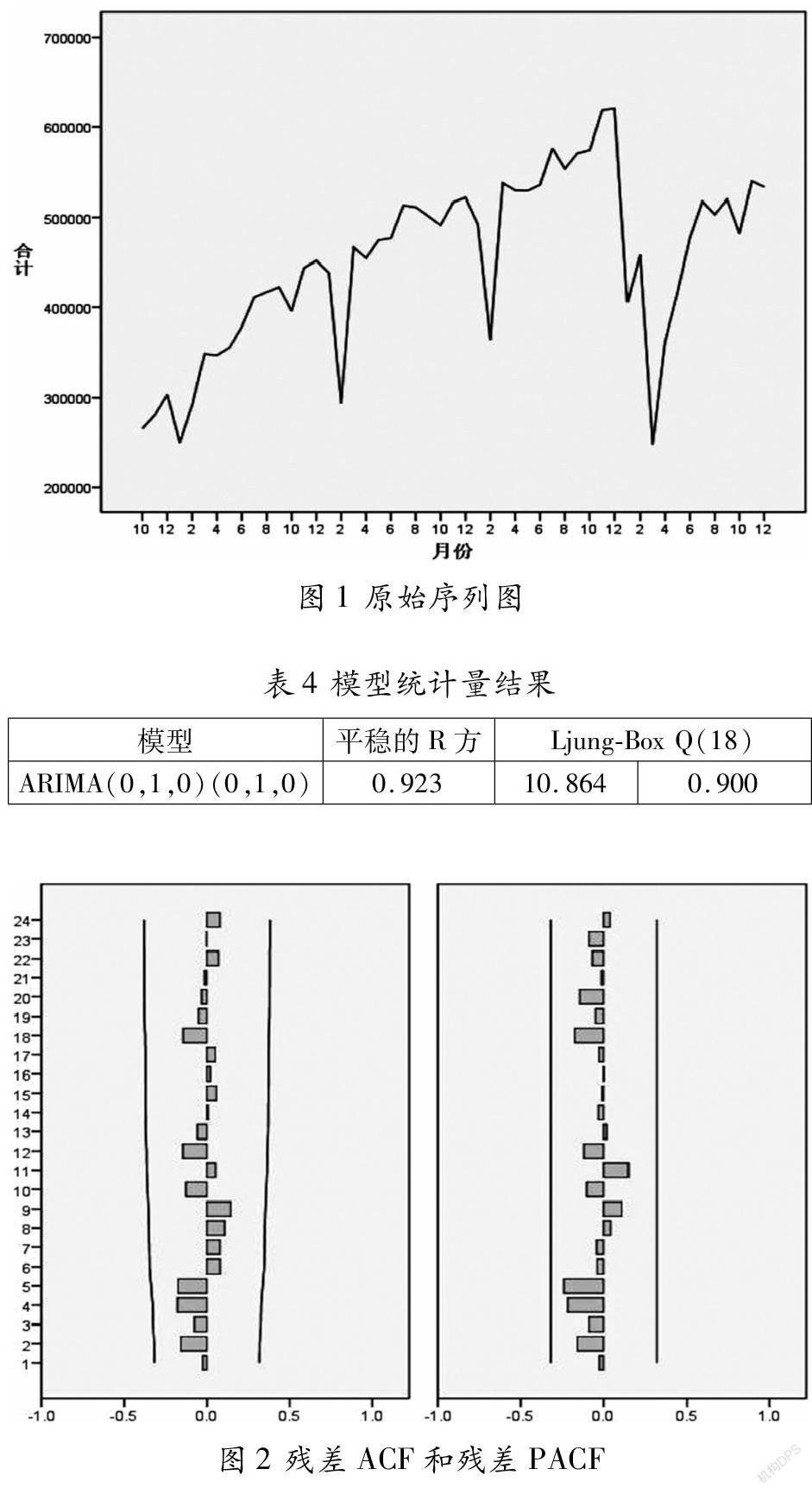
通过SPSS软件对全线的月均客流量进行时间序列图分析，从图1可以看出，该原始序列有一个较明显的季节特征，年度高点位于12月，为了序列图更趋平稳化，采用了差分和季节性差分对数据进行时间序列平稳化处理，得到平稳化序列图。

3.4案例模型构建与验证

通过SPSS软件，创建专家建模器预测模型（仅限ARIMA预测模型），如表4所示，所建立的ARIMA模型的因变量标签为“全线”，模型名称为“ARIMA”，模型的类型为ARIMA（0，1，0） （0，1，0）。

表4给出了模型的拟合統计量和Ljung-Box Q统计量。平稳的R方值为0. 923，与模型拟合图中的平稳的R方一致，能够解释时间序列约92. 3%的变化规律。得出统计量值为10.864，显著水平为0.900。可以说明ARIMA（0，1，0）（0，1，0）模型对全线客流量的拟合情况是非常不错的。

完成模型建立后，对残差序列进行自相关检验，SPSS软件计算的残差做残差序列的ACF和PACF如图2所示。由图可知，残差序列为白噪声序列，ARIMA（0，1，0）（0，1，0）模型通过检验，可以确定ARIMA（0，1，0）（0，1，0）模型为预测深圳地铁七号线未来年客流量较为适合的模型。

3.5未来两年的全线客流量预测

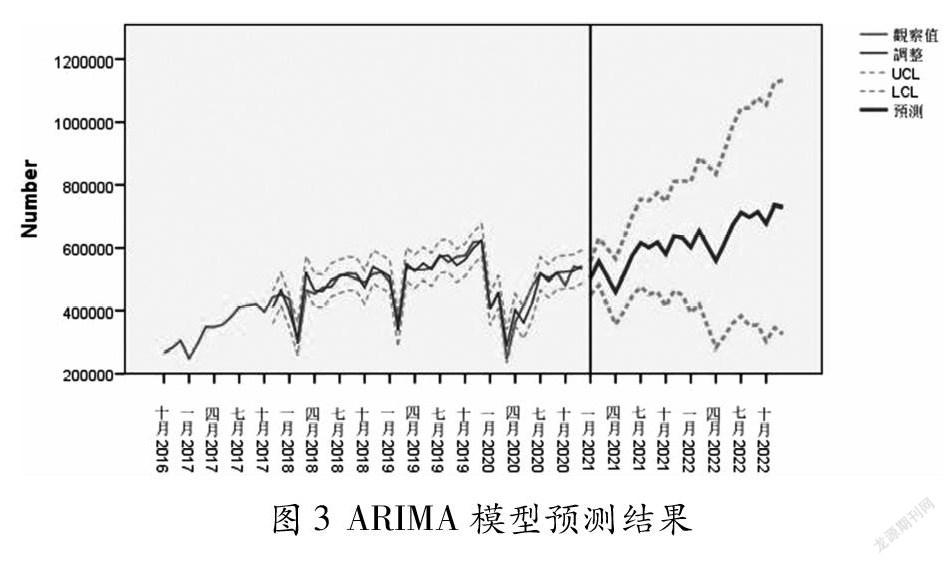
通过ARIMA（0，1，0）（0，1，0）预测模型，对深圳地铁7号线未来两年（2021-2022年）的月均客流量进行预测，预测结果如图3所示：

4结论及反思

运用所建立的组合模型对城市轨道交通线路进行客流量预测，分析其运营状况。另外，还可以寻求出更多针对特点线路的预测方法及拟合模型，以得到更贴近事实发展的客流数据。除此之外，为车站客流控制和安全管理、轨道交通线路的规划与发展提供了理论支持。现得出以下结论：

（1）一般而言，深圳地铁7号线客流量在样本期间波动幅度较大。另外，从指标来看，全线客流量均值较高，可见在样本期间该线的运营状况良好。

（2）深圳地铁7号线客流量在样本期间呈波动上升态势，并且在样本期间的波动不是很大，得出数据拟合较好的ARIMA（0，1，0）（0，1，0）模型，可更好地预测出其未来全线的客流数据。

（3）在城市轨道交通运营管理过程中，通过预测客流，有利于合理规划列车运行方案日后运营能够进行合理判断和决策。但由于客流的分布特征广，客流量影响因素多，目前采用的研究数据样本较少，进行客流预测精准度有限，考虑更多相关变量、使用更大样本数据将是下一步要探索研究的方向。

作者简介：文晶琳（1999— ），女，汉族，广东南海人，本科，研究方向：交通运输规划与管理。