悬链斗卸船机臂架悬挂点的位置计算与优化

2020-12-30杨大海崔益华邵海林

港口装卸 2020年6期

关键词：臂架吊点皮带机

杨大海崔益华邵海林

南通润邦重机有限公司

1 引言

悬链斗卸船机具有卸船效率高、清仓量小、综合使用成本低等优势，但是针对此种机型的设计资料较少，也不够细化。实际项目中，臂架设计的悬挂吊点位置及臂架车轮安装距的设计对整机至关重要，若设计不当会出现整机安全及使用性能不达标等问题。

2 悬链斗卸船机的特点及设计难点

2.1 悬链斗卸船机特点

悬链斗卸船机通过臂架上悬挂的自由悬垂链斗在船舱内进行取料，链斗机构将物料提升后卸载到臂架皮带机上，再通过臂架皮带机转运到码头后方输送系统，从而完成卸料。悬链斗机构安装在可在臂架上来回移动的小车上，主臂架通过钢丝绳与平衡配重相连而悬吊着，臂架的升降依靠俯仰钢丝绳进行(见图1)。臂架为三角形结构，根部上、下分别设有车轮组，沿门架海侧门腿的内、外侧移动[1-2]。整个臂架系统是一个自由状态，由于小车在臂架横梁上运行，根部车轮承载随小车位置变化而变化，继而影响整个门架的受力状态。

图1 整机设备图

2.2 设计难点描述

总体设计中臂架的吊挂点位置至关重要。吊点靠前，臂架的平衡性不够，当悬链机构在非工作极限位置时车轮会脱离轨道，存在安全隐患。吊点太靠后，工作时臂架的车轮轮压会超过许用值。臂架的吊点及车轮安装距的设计直接影响到臂架车轮的轮压、臂架的稳定性、继而影响臂架及门架结构的受力及刚性。

3 现有计算及问题分析

基本受力分析见图2。针对臂架吊点位置的初选，常规的计算方法如下。

图2 受力分析示意图

要保证悬链处于海侧极限位置时，车轮组轮压不大于许用轮压：

(1)

非工作悬链处于陆侧极限位置时轮压为正：

(2)

得出吊点的范围为：L1min≤L1≤L1max。

式中，L为臂架吊点到门架中心的距离，m；∑M为悬链处于海侧极限位置时，臂架上所有零部件的力矩和，Nm；∑G为悬链处于海侧极限位置时，臂架上所有零部件的力矩和，Nm；∑M′为悬链处于陆侧极限位置时，臂架上所有零部件的力矩和，Nm；∑G′为悬链处于陆侧极限位置时，臂架上所有零部件的力矩和，Nm；G1，G2，G3，……Gi为悬链处于海侧极限位置时，臂架上各部件的载荷，如臂架自重、链斗机构自重、皮带机自重等，N；L1，L2，L3，……Li为悬链处于海侧极限位置时，臂架上各部件的载荷选对门架中心对应的力臂，如臂架自重力臂、链斗机构自重力臂、皮带机自重力臂等，m；G′1，G′2，G′3，……G′i为悬链处于海侧极限位置时，臂架上各部件的载荷，如臂架自重、链斗机构自重、皮带机自重等，N；[P]为车轮的许用轮压，MPa；H为上下车轮的距离，m。

按以上步骤可以确定吊挂点的范围，但是存在如下问题：

(1)计算所得值范围较大，具体在哪一个位置是最优值无法得出，不能满足实际工程应用中选取一个确切的点或一个较小的范围值的要求。

(2)在实际项目中，还存在后方皮带机的自重G和吊挂点的拉力F，这2个力对整个臂架的吊点位置选择有很大影响。

(3)以式(1)、(2)计算出来的范围可能会不存在，需要调整上下车轮组间距H的数值才能满足实际工程需要，即H也是一个待优化的变量，需要探究L1与H之间的关系。

4 优化思路及方法

4.1 优化思路

针对以上问题，对此吊点的确定给出一个臂架优化的解决方案，为后续的实际项目提供指导和借鉴。

实际项目中，链斗机构的两个极限位置是根据船型确定的，最大轮压则是根据门架结构受力确定的。在这个系统中，臂架上下车轮组安装间距H及臂架吊点位置L1是可调整的。所以优化思路为：以H、L1两个变量建立优化函数。

4.2 计算方法

以臂架根部上车轮组为铰点建立力矩平衡，以小车在臂架横梁上两个极限位置为计算工况，计算过程如下。

悬链处于海侧极限位置时，移动臂架系统受力分析见图3。

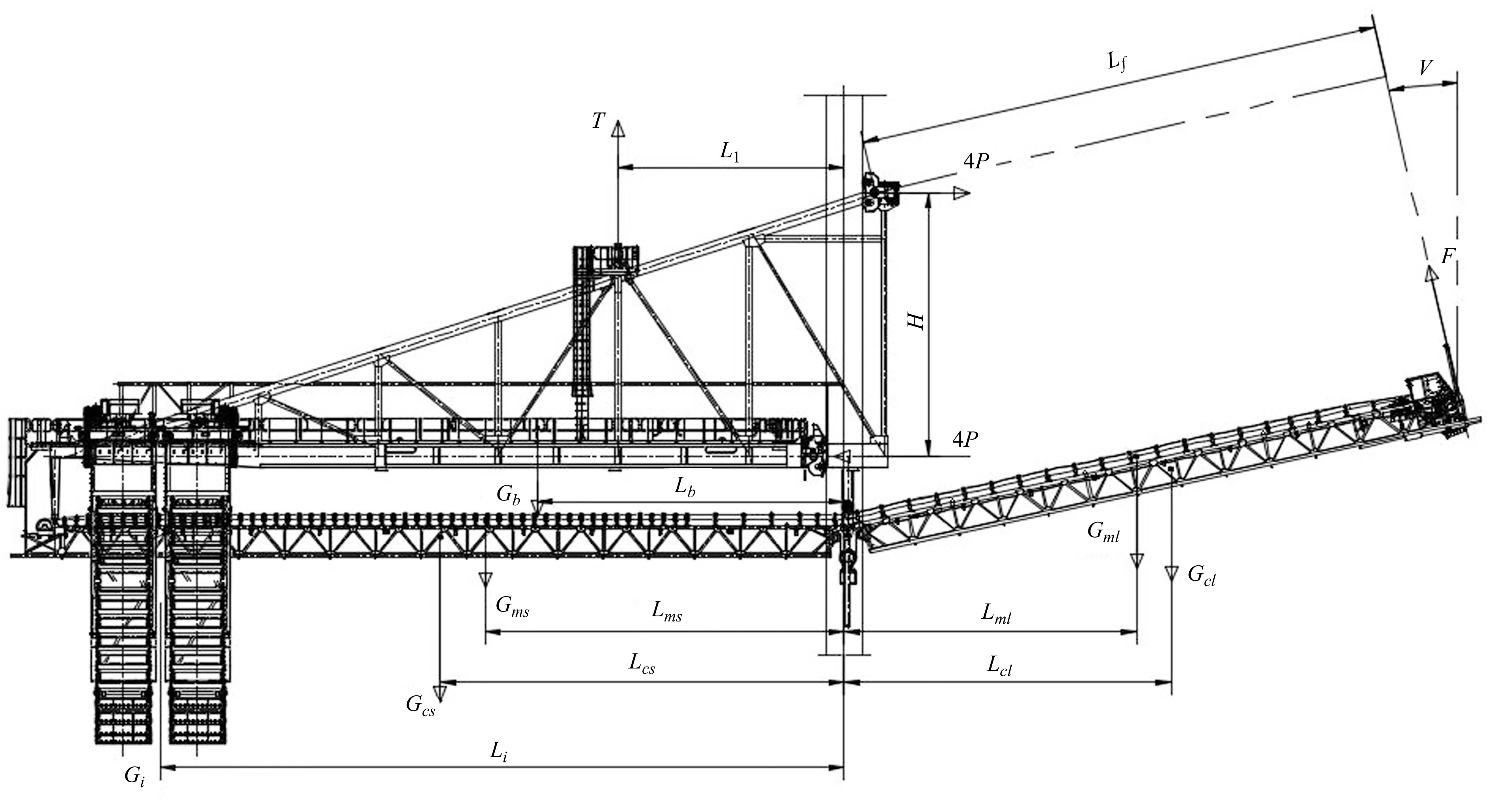
图3 海侧极限位置受力分析图

TL1+4PH=GbLb+GmsLms

+GcsLcs+GiLi+GmiLi-GmlLml

-GclLcl+FLf

(3)

式中，P为工作最大轮压，KN；Gi为链斗及运行小车机构重力，t；Gb为悬臂梁桁架金属结构重量，t；Gms为海侧皮带机物料重量，t；Gcs为海侧皮带机及机架重量，t；Gmi为链斗中物料的重力，t；Gml为陆侧皮带机物料重量，t；Gcl为陆侧皮带机及机架重量，t；F为吊挂点的拉力，kN。

非工作悬链处于陆侧极限位置，移动臂架系统受力分析见图4。

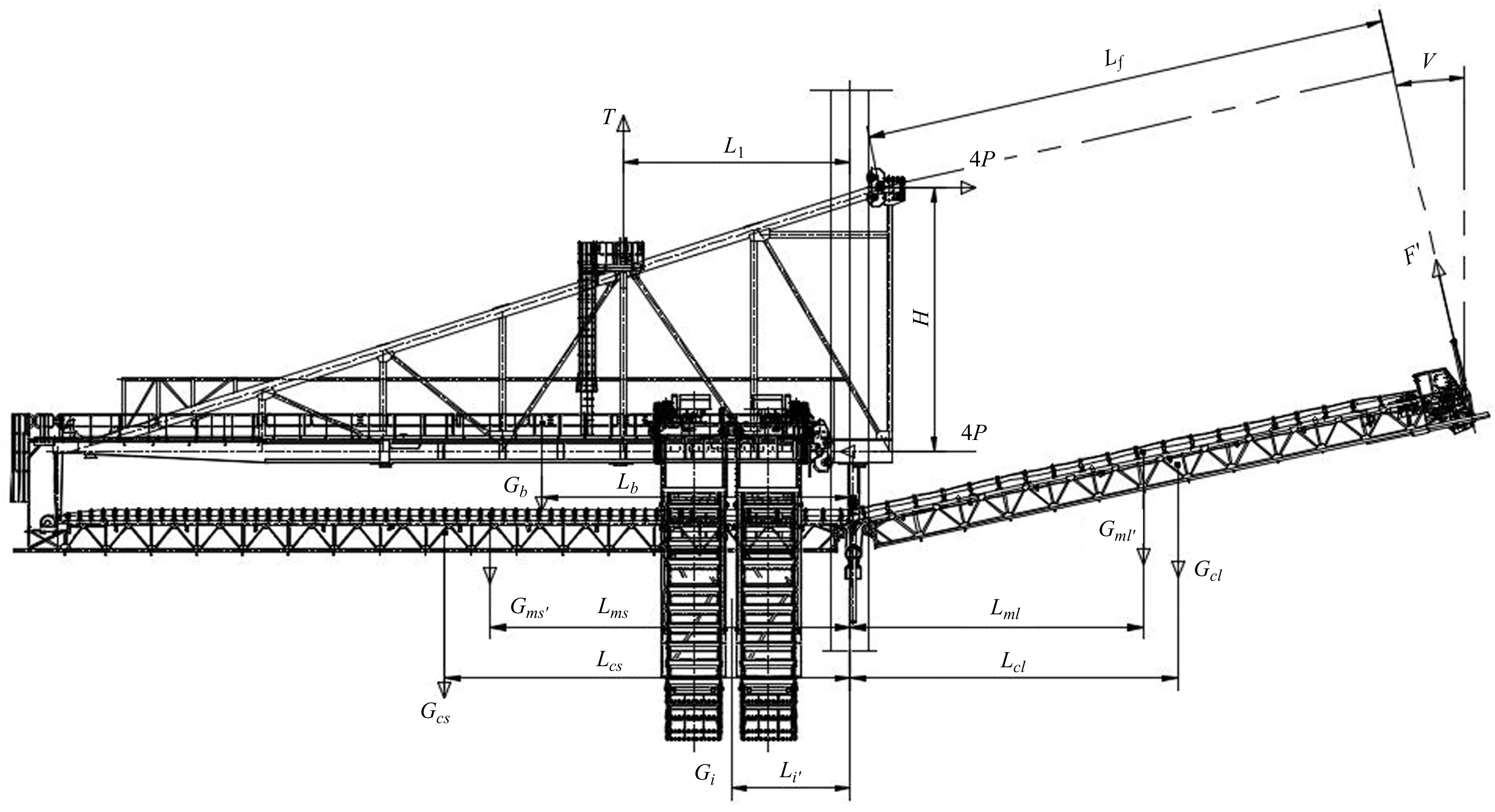
图4 陆侧极限位置受力分析图

(4)

式中，P′为非工作最小轮压；Gms′=0，Gml′=0，Gmi′=0，则：

(5)

以上为两个工况下的力学平衡式，由于其活动载荷一定，现用式(3)减去式(5)，去除无关因素，从而得出与自身结构相关的关键因素：

(T-T′)L1+(4P-4P′)H

=GmsLms-GmlLml+Gi(Li-L′)+GmiLi+(F-F′)Lf

(6)

式中，(F-F′)仅是物料变化引起，即

F-F′=0.5Gml/cosv

(7)

式中，(T-T′)为取料及输送系统上物料变化引起的载荷，即

T-T′=Gms+Gml/2+Gmi

(8)

令GmsLms-GmlLml+Gi(Li-L′i)+GmiLi+(F-F′)Lf=K，整理后得：

(9)

极限状态下，最大轮压为许用轮压，最小轮压为零，则得出吊点与车轮安装距的优化关系式如下：

(10)

L1为臂架吊点X方向水平距离，H为上下车轮组Y方向垂直间距，L1与X的关系见图5。

图5 L1与H的关系图

4.3 设置边界条件

实际工程设计中，臂架吊点位置L1一定大于小车在陆侧极限位置L′i，小于小车在海侧极限位置Li的一半，即：L′i≤L1≤Li/2。在此范围内优化确定H值，从而得出确切的L1值的大小。

4.4 最终验证

通过以上得出吊点位置L1，臂架根部车轮安装距H，从而确定整个臂架的总体结构尺寸，在此基础上再确定门架的尺寸。整机布置确定后进一步验算各工况下车轮轮压和臂架受力。

5 实际应用

现以我司设计制造的额定生产率为800 t/h的悬链斗卸船机为例进行分析计算，基本参数见表1。

表1 基本参数

根据式(1)和式(2)，实际设计H为11.23 m时，计算出L1≤10.21 m，L1≥11.7 m，计算出的L1范围不存在。由于H为固定数值，无法得出想要的结果，必须将H设为变量，不断尝试改变H值的大小才能确定出满足要求的L1的范围。

根据按优化后式(10)的算法：设定工作最大轮压P=[P]=35 t，非工作最小轮压P′=0.1 t，得出：L1=237-17.78H。根据实际情况，L1的大体范围为L′i≤L1≤Li/2，从而计算出12.5≤H≤13。实际项目中，取H=12.5 m，L1=14.75 m。最后校核轮压及整机稳定性，满足使用要求。