拱形抗滑结构设计参数优化分析

2020-12-30夏英志王海恩

河南城建学院学报 2020年5期

夏英志，王海恩

(1.河南城建学院土木与交通工程学院，河南平顶山 467036;2.洛阳腾飞市政工程有限公司,河南洛阳 471000)

拱形抗滑结构是近年来提出的一种将传统抗滑桩和拱形结合起来的新型抗滑结构，其主要优势是可利用拱形结构的抗压性能来提高抗滑桩的加固效果，已有部分工程采用了该种抗滑结构进行加固。关于拱形抗滑结构，已有部分学者开展了相关研究：王辉[1]基于某矢跨比为110的拱形抗滑桩结构采用模型试验的手段对拱形抗滑桩墙的变形特性、受力特征、荷载传递模式进行了探讨，检验了该抗滑结构的成拱效果，并提出了几种拱脚约束手段；张志伟[2-3]基于空间结构的内力分布情况推导了拱形抗滑结构的内力计算公式，并将理论计算结果与模型试验结果对比，通过算例分析与悬臂桩及直线排桩抗滑结构比较，结果表明拱形连系梁对抗滑桩的位移约束效果明显；赵法锁[4]就锚碇拱形抗滑结构的空间布置对结构体系受力的影响进行深入研究，结果表明拱形抗滑结构能充分发挥混凝土材料抗压性能，是一种合理的空间受力体系。同时，以上研究均指出矢跨比和拱脚约束情况对结构的抗滑性能影响较大。

抗滑桩等非连续支档结构发挥作用的关键在于桩间土拱效应[5]，而承受滑坡推力后抗滑桩变形的大小主要是由桩体本身的尺寸和材料决定[6-7]。拱形抗滑结构兼具抗滑桩和拱形的双重结构特性，但抗滑桩和拱形的影响因素的主次关系尚缺乏研究。鉴于此，论文采用有限元法建立边坡的数值分析模型，运用正交试验的方法对拱脚约束条件(拱脚桩桩径扩大比)、拱形矢跨比、桩间距和桩径这4种影响因素对抗滑结构的力学特性和加固效果进行研究，并根据极差和方差分析结果得到参数的最优组合，以期为拱形抗滑结构的设计提供参考。

1 数值分析模型

1.1 模型概况

典型的拱形抗滑结构由桩顶的拱形连系梁和多根抗滑桩组成，如图1所示。以平面呈拱形排布的单排抗滑桩为例，建立拱形抗滑结构加固边坡的分析模型见图2。

以某铁路路堤边坡为例，为了消除模型的边界效应，模型的宽度取抗滑结构平面跨度的两倍；计算约束桩体绕Z轴旋转自由度，土体的底部约束Z方向位移，左、右侧面约束Y方向位移，前后侧面约束X方向位移。

图1 拱形抗滑结构

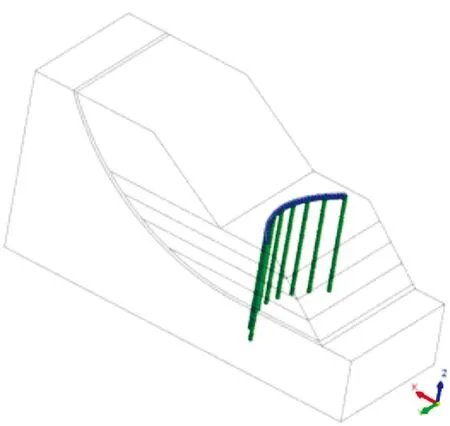
图2 拱形抗滑结构加固边坡示意图

1.2 计算参数

(1)拱形抗滑结构和土体

土体采用实体单元模拟，滑带土采用0.5 m厚的土层模拟，计算时采用摩尔库伦本构模型；抗滑桩采用梁单元，计算时采用弹性本构模型。拱形抗滑结构的抗滑桩和拱形梁材料均采用C30混凝土，桩截面设置为圆形，桩长13.5 m，锚固长度为5 m。土体参数根据该滑坡的详细岩土工程勘察报告进行选取，桩体的混凝土参数根据规范选取，具体的土体和抗滑结构参数见表1。

表1 土体和混凝土计算参数

拱梁的平面形状基于合理拱轴线公式计算所得，采用的合理拱轴线公式为：

(1)

式中：f为拱形梁平面上的计算矢高，l为拱形梁的计算跨径。

2 结构抗滑性能影响因素敏感性分析

敏感性分析是通过测定一个或多个影响因素变化所导致的指标变化幅度来评判该因素对指标的影响程度。对于抗滑结构抗滑性能的影响因素分析可以转化为以桩顶水平位移、桩身应力和坡顶沉降的多指标多因素的敏感度分析和显著性判断[8]。论文采用正交试验方法进行影响因素的敏感性分析，各因素对不同指标的敏感性和显著性分析通过极差分析和方差分析进行判断。

2.1 影响因素的选取

在采用抗滑结构对边坡进行加固时，抗滑结构的设计参数(桩截面形状和尺寸、桩长、桩间距、桩体力学参数等)、坡体参数(内摩擦角、黏聚力、弹性模量、泊松比等)、桩-土接触参数(法向刚度、切向刚度、最终剪力等)都是影响抗滑效果的因素[9-10]；对于拱形抗滑结构，拱形的矢跨比和拱脚的约束条件也是主要影响因素。对于特定的边坡，坡体的参数已经确定，因此不考虑坡体材料参数的影响；桩-土之间的接触特性根据公式基于土体和桩体进行计算，不再专门设置因素水平；拱形抗滑结构涉及桩数量多，宜采用圆形截面。综上所述，论文在进行试验时着重考虑拱形抗滑结构的参数(拱脚约束条件、矢跨比、桩间距、桩径)对结构的抗滑性能进行分析。

2.2 因素水平

选取拱脚位移约束条件(拱脚桩桩径扩大比A)、拱形的矢跨比(B)、桩间距(C)、桩径(D)为试验因素。各因素所代表的含义如图3所示。

图3 抗滑结构各参数含义

(1)拱脚约束条件(A)

拱形抗滑结构在承受水平方向的滑坡推力后，拱形梁体内部弯矩值较小，拱圈截面承受较大的轴向压力，最终拱圈内部的压力传递至拱脚部位，故拱脚部位的约束情况对结构的变形影响较大。部分学者提出在拱脚部位设置大直径抗滑桩或多根桩以约束拱脚处的变形情况[11]，故通过扩大拱脚桩的直径来改变拱脚的约束条件，其控制标准为拱脚桩桩径与内部桩桩径的比值，范围为1～1.75。

(2)拱形的矢跨比(B)

如图3所示，拱形抗滑结构的矢跨比的定义为拱高f与拱形抗滑结构平面跨度l的比值，矢跨比的大小对拱梁内部的内力有显著影响。坡体在滑动方向存在一定的坡度，在采用拱形抗滑结构对边坡进行加固时不宜设置较大的矢跨比，应设置为坦拱形式，故考虑将拱圈的矢跨比设置为0～0.2[12]，矢跨比为0时为直线型排桩。

(3)桩间距(C)

抗滑桩的间距是相邻抗滑桩形成土拱的关键因素，桩间距过大，土体从桩间流失，抗滑效果变差；桩间距过小则不能完全发挥桩体的抗滑作用。对于直线型布置的排桩，学者提出的合理桩间距为(2～5)d，d为抗滑桩的直径。对于拱形抗滑结构，论文所指的桩间距定义如图3所示。

(4)桩径(D)

抗滑桩的直径直接影响桩体的抗弯刚度，论文设置抗滑桩的直径取值范围为1～1.75 m。

根据前述因素水平分析的结果所设计的因素水平如表2所示。

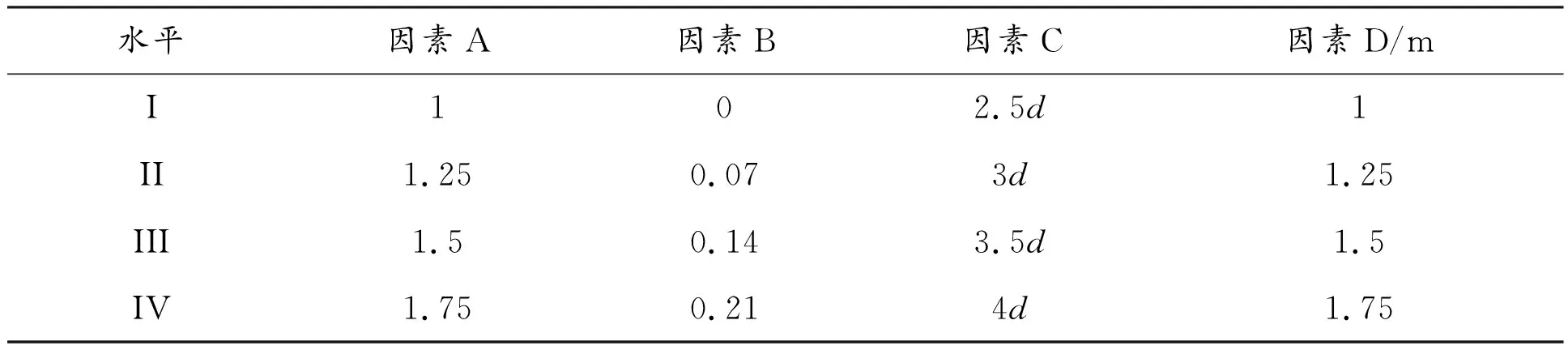
表2 因素水平表

2.3 正交试验设计

根据试验因素和水平情况，一般可采用4因素4水平的正交试验，但考虑到试验过程中可能存在误差，故在根据所选正交表安排完因素后，再设置一列空白列用于考察试验误差。鉴于此，选择L16(45)正交试验表格，根据正交试验表的设计，共进行16次试验，正交试验表如表3所示。

试验过程中，荷载的施加方式为面均布荷载，为了保证每个模型中的抗滑结构承受同样大小的滑坡推力，设定坡顶承受的总压力，采用该压力除以坡顶受荷面的面积得到每个模型坡顶均布荷载值。

表3 正交试验表

2.4 极差分析

正交试验影响因素的敏感度通过极差分析体现，极差指各因素各水平对应试验指标均值中的最大值与最小值之差。极差是衡量数据波动大小的重要指标，极差越大则该因素对指标的影响越大，可以通过各因素极差的排序确定因素对指标影响的主次关系。表4～表6分别为不同评价指标的极差分析表，表中(i=1,2,3；j=1,2,3,4)表示评价指标i在j水平时的试验结果的平均值。R为某个影响因素的最小值和最大值的差值，即极差。各因素对桩顶最大水平位移、桩身最大拉应力和坡顶沉降值影响的极差分析结果见表4～表6，表中A、B、C、D的含义见2.2。

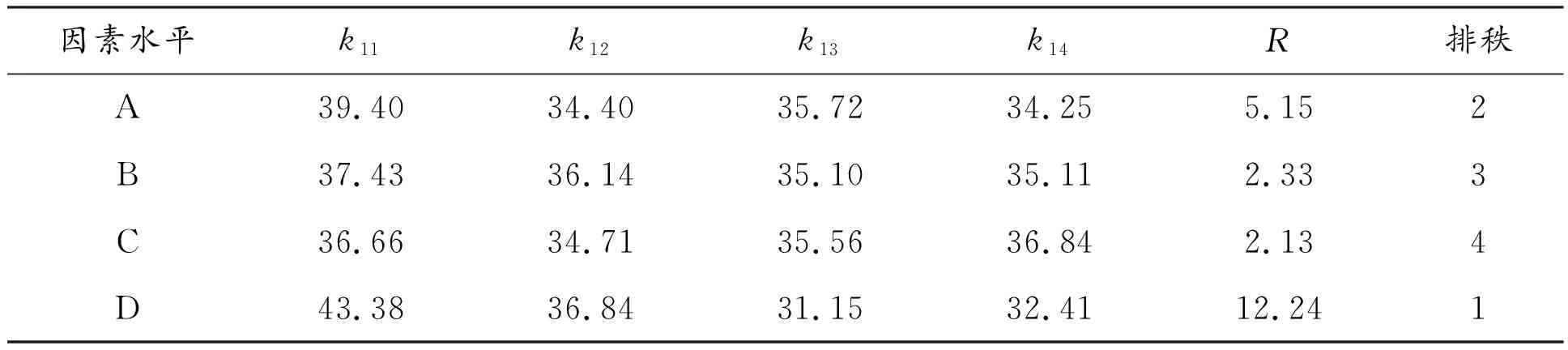
表4 桩顶最大水平位移极差分析结果 mm

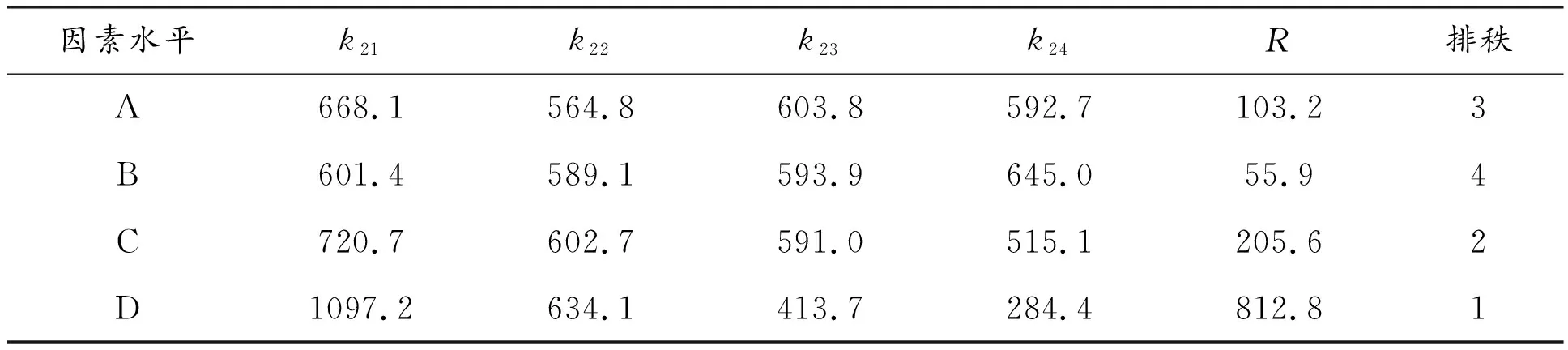
表5 桩身最大拉应力极差分析结果 kPa

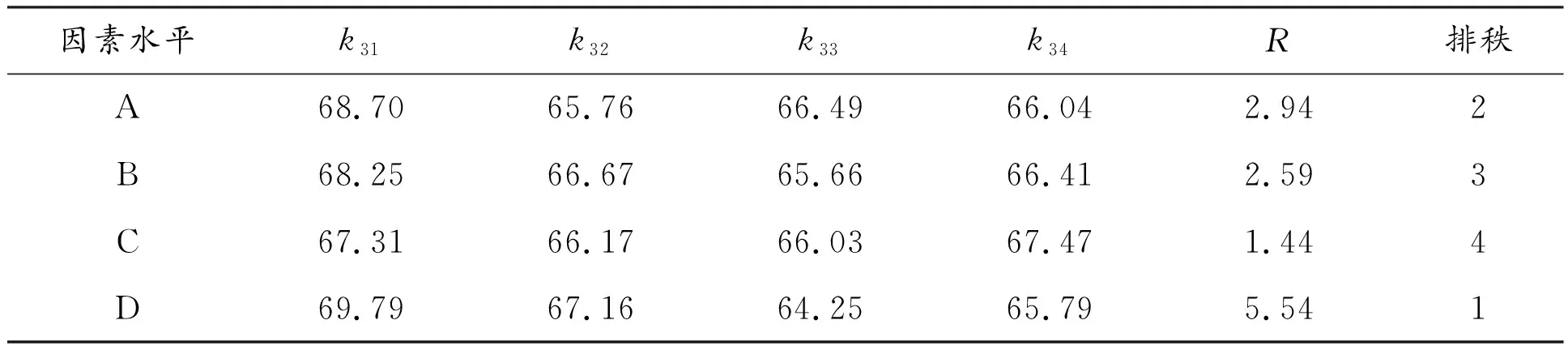
表6 坡顶最大沉降值极差分析结果 mm

由表4可知：对于桩顶最大水平位移，桩径对应的R值最大，桩间距次之，矢跨比对应的R值最小。各因素对桩顶最大水平位移影响的主次顺序为：桩径>拱脚约束条件>矢跨比>桩间距。

由表5可知：对于桩身的最大拉应力值，桩径对应的R值最大，桩间距次之，矢跨比对应的R值最小。各因素对桩身最大拉应力影响的主次顺序为：桩径>桩间距>拱脚约束条件>矢跨比。

由表6可知：对于坡顶的最大沉降值，桩径对应的R值最大，桩间距次之，矢跨比对应的R值最小。各因素对桩身最大拉应力影响的主次顺序为：桩径>拱脚约束条件>矢跨比>桩间距。

2.5 趋势图分析

为了直观反映各影响因素对评价指标的影响情况，寻求最优的因素水平，将影响因素的水平作为横坐标，纵坐标为评价指标，作出参数水平与各评价指标的趋势图，见图4。图4中落差较大的线条代表的因素是主要因素，落差较小的线条表明该因素为次要因素。

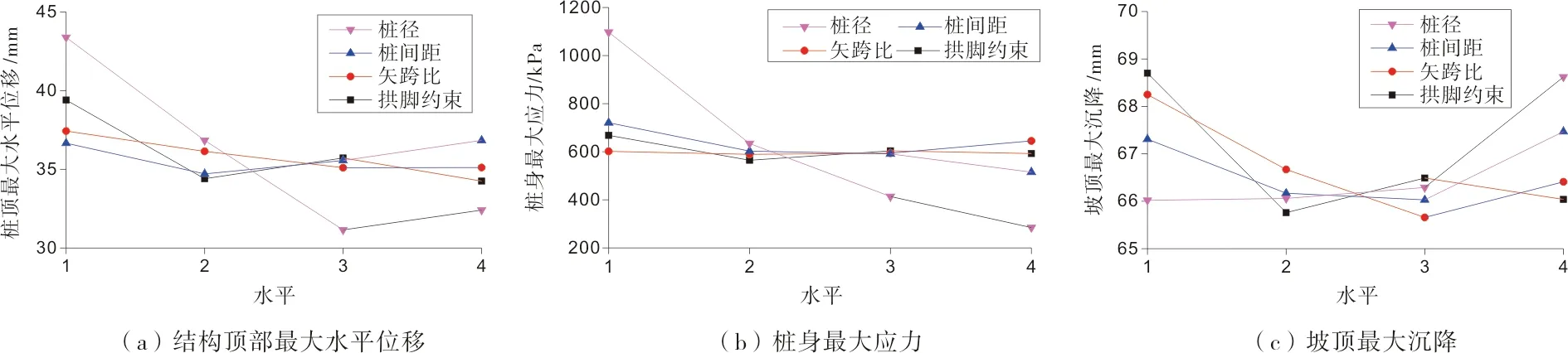
图4 各水平变化趋势

2.6 方差分析及显著性判断

(1)方差分析

根据正交试验结果，各因素对桩顶最大水平位移、桩身最大拉应力和坡顶沉降值影响的方差分析结果见表7～表9。

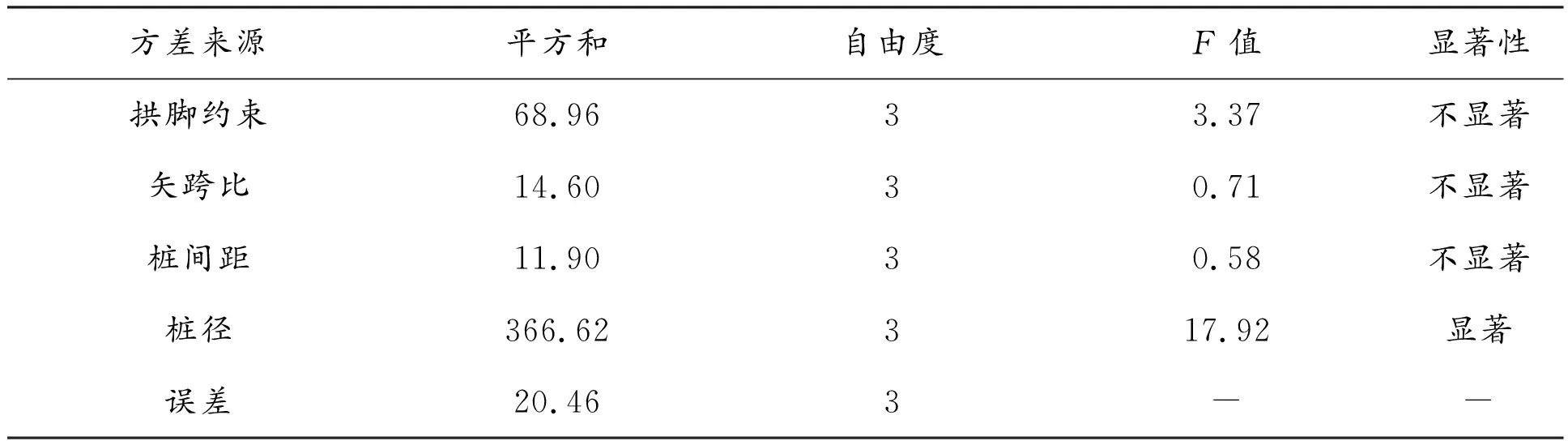
表7 桩顶最大水平位移方差分析结果

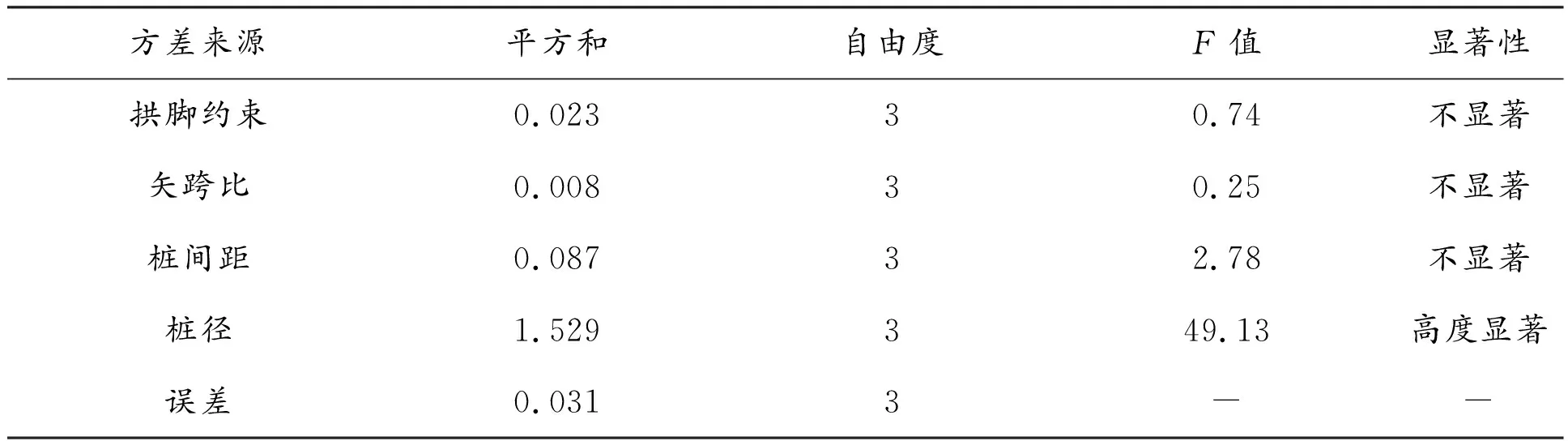
表8 桩身最大拉应力方差分析结果

表9 坡顶最大沉降方差分析结果

(2)显著性判断

为了弥补样本极差值不能判断所考察因素对试验指标影响是否显著，并估计试验误差，进一步采用方差分析的手段判断各因素对指标的影响程度，即判断各因素影响的显著性。在方差分析中，根据统计值F与给定的显著性水平α的临界值Fa进行比较，确定对原假设接收或拒绝。若F>Fa，则拒绝原假设，表明所检验的因素对评价指标有显著影响；若F≤Fa，则接受原假设，表明所检验的因素对评价指标无显著影响。取显著性水平α值为0.01和0.05，当F≤F0.05(r-1,n-1)时，影响因素不显著；当F500(r-1,n-1)≤F≤F0.01(r=1,n-1)时，影响因素显著；当F>F0.01(r-1,n-1)时，影响因素高度显著。r和n分别为误差自由度和影响因素自由度。

查F分布表得：F0.01(3,3)=29.5、F0.05(3,3)=9.28。将表7所得的F值与临界值相比较，可得：桩径对桩顶最大水平位移评价指标的F值大于F0.05，小于F0.01，所以桩径对桩顶最大水平位移的影响显著。将表8所得的F值与临界值相比较，可得：桩径对桩身最大拉应力评价指标的F值大于F0.01，所以桩径对桩身最大拉应力的影响高度显著。其余各影响因素对各评价指标的影响均不显著。

综上所述：桩径对桩顶最大水平位移的影响是高度显著的，拱脚约束、矢跨比、桩间距对桩顶最大水平位移的影响是不显著的；桩径对桩身最大拉应力的影响是显著的，拱脚约束、矢跨比、桩间距对桩身最大拉应力的影响是不显著的；桩径、拱脚约束、矢跨比、桩间距对坡顶沉降值的影响均是不显著的。

3 综合优化分析

最优因素水平的选择应与评价的指标相匹配，若要指标越小越好，则应选择最小指标所对应的水平。反之，则选取最大指标对应的因素水平。对于抗滑结构的抗滑性能来讲，各指标的值均为越小越好，因此可得到不同指标影响因素水平的最优组合，见表10。

表10 不同评价指标最优因素水平组合

结合极差方差分析结果可知：桩径对各评价指标的影响虽然均为最大，但其显著程度却差异较大，桩径对桩身变形和内力的影响为高度显著和显著，但对坡顶变形情况的影响却不显著，可见拱形的存在对结构的加固效果产生了一定的影响。

分析表10可知：对于因素A(拱脚约束)，对桩顶位移指标所对应的最优水平为1.75，其对桩身最大拉应力和坡顶最大沉降值指标所对应的最优水平均为1.25。实际工程中抗滑结构可以发生一定的变形，为了控制加固体的变形情况和结构安全性，因素A取1.25。对于因素B(矢跨比)，其对桩顶最大水平位移、桩身最大拉应力值和坡顶沉降值的影响分别排在第4位、第4位和第3位；由于各试验中桩体的最大拉应力均未超过允许拉应力，从控制坡顶沉降值角度和影响权重考虑，取矢跨比为0.14。对于因素C(桩间距)，在兼顾加固体的变形和结构安全方面，其取值为3.5d；对于因素D(桩径)，其值则需根据滑坡推力和加固要求综合确定。