地震层速度模型编辑系统应用研究

刘旭跃

(中国石化 石油物探技术研究院,南京 211103)

0 引言

随着地震勘探技术快速发展，勘探区域逐渐扩大，地表条件和地质构造越来越复杂。通过收集分析地震波，能够反演地下构造的分布情况，有助于针对性地进行油气勘探，提高开采效率。因此精确地计算出地震波的传播速度是地震资料处理和解释的关键问题。地震勘探的采集精度一直在提高，分析面元不断减小，常规的速度分析方法不能满足精细构造成像的要求[1]，利用有效的地震速度分析方法，建立精确的速度模型成为地震勘探的核心问题之一，关系着整个地震成像的质量和最终解释结果[2]。地震速度建模方法的相关研究非常活跃[3]，就当前的实际应用而言，基于层析反演理论的速度建模方法仍是主流应用技术[4-5]。

在常规叠加处理时，都会进行速度分析，速度分析时，不论是自动或手动拾取速度点，拾取的速度谱以及沿层速度内插后，会存在速度误差[6]，为减少速度异常值，通过分析速度拾取层的谱信息，对速度值进行修整，进一步优化速度场，更新速度模型，以达到提高速度精度的目标。笔者研究开发了层速度模型编辑系统，采用Qt面向对象编程语言，读取绘制层速度模型图像，通过鼠标滑动，实时列出CDP和line对应的速度值，图像的不同颜色代表不同的速度值范围，直观地显示速度变化。在异常值附近选择指定区域，就会出现速度矩形列表分析图，选定某列矩形，就会选定速度区域，清除后，可采用线性插值或优化后的克里金插值法进行速度插值，实现精准去除速度异常值，提高整体速度精度。与国外主流的商业软件相比，本系统采用文件式I/O磁盘读取和自定义数据结构体管理，针对自主研发的复杂区域速度建模方法研究而开发，操作简单，采用Qt语言开发，支持跨平台应用，易于移植、扩展和后期维护。

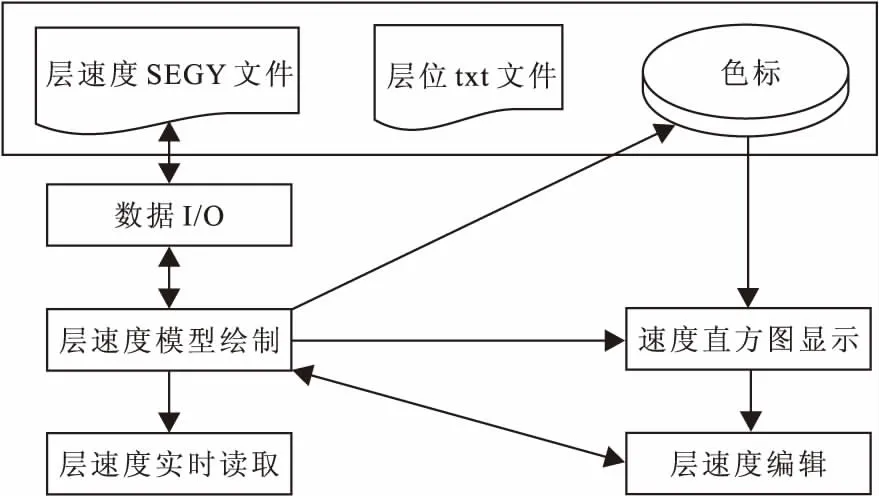
图1 系统架构图Fig.1 System architecture diagram

1 系统设计

根据沿层速度模型编辑的需求，系统开发的功能有：速度模型加载和输出模块、层速度显示模块，速度直方图显示模块、层速度编辑模块、色标显示模块(图1)。

图1中，数据I/O从磁盘中根据层速度SEGY文件的结构和层位文件格式读取数据或输出数据；层速度模型绘制：加载的层速度文件经过坐标转化，将速度值对应于屏幕坐标值，映射为像素颜色值RGB(红、绿、蓝)，转化为二进制图像绘制出来。可以选择层位文件，从文件中读取该层的速度值，并在原来图像上绘制层位图；层速度实时读取：通过图像交互功能，鼠标在图像上移动时，把屏幕坐标转为图像坐标，搜索对应的速度值，在显示区域把速度值显示出来；速度直方图显示：根据存储在二维数组中的速度值和一维数组中的色标颜色值。用鼠标在速度图上拖动一个矩形框，在主界面的右下角区域绘制速度直方图。直方图由多个小矩形组成，每个矩形代表一个速度区域，鼠标选中矩形，在速度图上突出显示相应的速度；层速度编辑：对层速度图像中速度值编辑。

层速度编辑模块操作流程如下：

图2 速度编辑流程Fig.2 Speed editing process

图3 线性插值图Fig.3 Linear interpolation graph

层速度编辑分为两个步骤：①清空;②插值。可以选择3种方式进行插值:①线性插值;②权重线性插值;③克里金插值。色标显示模块可以选择色标面板中的任意一组，色标值变化，直方图也会改变。清空时，会在插差值显示区把清空区域的色标显示出来，便于对比效果。

2 关键技术

2.1 线性插值

线性插值方法在数学和计算图形学等学科领域应用非常广泛,它简便易用，连续性好[7]。

如果有两个点坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间范围内的x在两点直线上的值，如图3所示，计算得到(y-y0)(x-x0)/(y1-y0)(x1-x0)

如果方程两边的值是α，则从x0到x的距离与从x0到x1距离的比值就是求取得到的插值系数。因为x值是之前已经知道的，所以从公式(1)计算得到α的值。

α=(x-x0)/(x1-x0)

(1)

同理,α=(y-y0)/(y1-y0)

(2)

那么，用数学方程式考虑就可以表示成为：

y=(1-α)y0+αy1

(3)

或者，

y=y0+α(y1-y0)

(4)

采用这种计算方法，求取α值就可以直接知道y。事实上，假如x不是[x0,x1]区间范围内的值，并且α也不在[0,1]范围内，上述的数学公式也是成立的。

2.2 距离反比权重插值

距离反比权重插值(Inverse Distance Weighted，IDW)基于样点相近相似的原理，也是一种广泛使用的简单空间插值方法，权重采用插值点与样本间的距离得到，然后进行加权平均，由此可见，距离插值点越近的样本点，对它赋予的权重值就越大,该算法简单且时间、空间复杂度相对都很小[8]。假如二维平面上有一系列的无规则的离散点，给出它们坐标和值为Xj、Yj、Zj(j=1,2,3,…,n)。z点值通过距离加权值求取得到。Z值的计算公式如下：

(5)

(6)

它是一种比较简单又有效的数据内插方法，而且运算速度也算较快。距离反比权重插值的重要影响因子除了权重距离外，查找半径和幂次也是它非常重要的影响因子。定长查找是在指定半径范围内的所有采样点都要运用到栅格单元的插值运算中。假设在之前假定的半径范围内参与内插计算的采样点个数比指定的最小数目小，那么将查找半径继续扩大，使得它能够包含更多的采样点，从而确保参加计算的采样点个数满足之前指定的最小数目。

2.3 克里金插值方法

克里金方法是根据协方差函数对随机过程或随机场进行空间建模和预测的回归算法[9-10]。它是从地统计学里面逐渐发展改进而形成的，能够对z值的离散点通过数学公式进行分析运算，它可以被称为一个线性的数学估计系统。只要固有平稳随机场能用各向同性假设满足的话，都可以采用克里金算法计算。它包含多种算法，也可以叫做空间最优无篇估计器，经过多年发展，衍生出很多改进算法，比如协同克里金、泛克里金等，近年来随着人工智能的发展，它逐渐与其他算法结合起来，形成新型算法，比如神经网络克里金、回归克里金、贝叶斯克里金等。无论怎么改进，它的算法是为了精确地产生预测表面，不断提高度量预测的准确性以及确定性。克里金方法说明表面变化的空间相关性通过假设采样点之间的距离或者方向。它确定每个位置的输出值，采用数学拟合过程，将指定数量的值或者是一定范围内的全部值通过数学函数来计算。而且它不是简单的计算，要经过一个以上的操作才能产生。比如说，它研究方差表面、变异函数等，克里金方法比较适合数据中存在空间相关距离或者方向偏差，通常应用的领域有土壤科学和地质研究中。

克里金方法与反距离权重法有点相似，都可以对附近的测量值进行加权来得出未测量位置的预测，通常将加权总和算法运用到这两种插值方法里面：

(7)

式中：Z(si)为第i个位置处的测量值;λi为第i个位置处的测量值的未知权重;s0为预测位置;N为测量值数。

从上数公式可知，权重的值是由计算点在整个随机场里的位置关系而确定的，不单单由计算点自身所处的空间位置和计算点间的距离得到的，它的固有平稳随机场的数学期望都是一样的，本系统可以选定需要计算点的范围，把数值点的 CDP和Line保存起来，得到计算点的空间位置。在各向同性假设下，计算点的数学期望在固有平稳随机场中，与它自身的空间方位没有任何关系。一般采用变异函数当做它的近似值，在运算中还可以采用拉格朗日乘数法来进行计算，得到克里金算法的方程组。

采用克里金插值方法处理数学计算任务时，一般都是要完成两个目标，首先是要通过分析数据，找到数据相互间的联系和规律。然后就是开始对待求解的数值点通过拟合等过程，进行预估，使之不断逼近精确值。在算法实现方面，最开始要设置一系列运算中需要采用的变量及函数值，比如说变异函数以及协方差函数，拟合模型的统计相关性有关的一些值可以用创建的函数来预估。接着就是通过公式，对需要求解的数值进行预测。在实现的过程中，算法采用的数据是不一样的，最初是估算要求解值的空间自相关，得到该值后，随后再对要求解值预测。

拟合模型或空间建模可以称为变异分析或者是结构分析[11-12]，需要求解的数值，必须放在它自身所处的空间模型中来分析，围绕指定区域内的所有空间点来计算，利用经验半变异函数的图像进行处理。

图4 经验半变异函数示例Fig.4 Examples of empirical semi-variograms

一般情况下，每个位置的数值点之间的空间位置都是固定的，每个点是不一样的，这样的话，它们的空间点对就有很多种表达方式。在很短时间内要找出空间内全部数值点对，并且在图像中显示出来，这将是件困难的事情。比方说，给定一个范围内的数值点，要找出这个范围内全部数值点对的平均方差，采用经验半变异函数来表示的话，如图4所示，横向数值是距离或者表示步长，纵向数值代表平均半变异函数值。

空间自相关是表示变量数值在一个指定区域内与其他数据之间存在的相互依赖关系。在进行空间自相关量化时候，可以遵循空间位置的逻辑规律作为评判准则。认为离待求的数值越近，关联性越高，离待求的数值越远的话，关联性越小。在图4中表示，在坐标轴x轴的最左边，空间数值对的距离相对来说会小，那么它们的关系就更加密切，纵向看的话，就是在y轴的靠下方。在坐标轴x轴的最右边，空间数值对的距离相对来说会大，那么它们之间的关系就疏远，纵向看的话，就在y轴的靠上方。

将经验半变异函数生成的数值进行拟合，得到数值模型。这个过程中，若想精确的对数值空间进行估算和预测，就要注重半变异函数建模的环节。通过对区域内数值点的空间属性估算，利用经验半变异函数来得到待求数值的属性以及它们之间的空间自相关信息。采用计算连续函数来得到经验半变异函数拟合模型，能够让克里金法计算中的克里金方差大于零值，即便不知道所有数值点的空间属性的情况下，也能拟合出连续的函数曲线，以方便分析和预测。

如果在计算时发现经验半变异函数产生的数值与数值模型之间有一些不同，也可认为是存在一些误差，拟合模型的曲线中，有部分数值大于拟合曲线的值，有部分数值小于拟合曲线的值。可以给出一个参考的空间距离值，待求数值就会全部大于拟合曲线的值，或者给出一个参考的空间距离值，待求数值就会全部小于拟合曲线的值，满足这种情况时，这个半变异函数模型就达到要求。

3 系统实现

本系统基于Linux平台开发，采用文件存储方式。由于系统需要图形显示和交互，鉴于Qt跨平台的C++图形用户界面应用程序开发框架，适用于GUI程序开发，故采用Qt作为开发环境。

沿层速度模型加载时，首先从工区里筛选出符合沿层速度模型文件后缀的数据。

1)从中选出沿层速度模型文件。

2)根据该文件结构体，找出与速度模型文件相关的层位文件。

3)选出层位文件，读出层位的速度值。

它们之间的关系采用结构体链表表示(图5)。

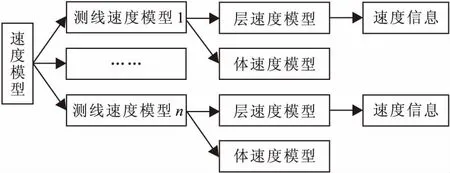
图5 速度模型结构体关系Fig.5 Velocity model structural body relation

在绘图区域里，用不同颜色代表不同速度值进行对应绘制(图6)。

图6 层速度图Fig.6 Interval velocity map

当鼠标在绘图区域滑动时，在信息显示区会根据CDP和Line值显示速度值(图7)。

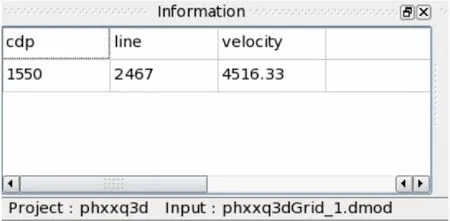
图7 信息显示图Fig.7 Information Display Chart

直方图显示是根据速度范围进行绘制。操作步骤如下：

表1 插值结果

插值完成后，保存速度模型文件

1)速度模型图绘制完成后， 点击直方图按钮。

2)用鼠标在图形中选择需要浏览的区域。

3)利用窗口坐标与速度值之间的关系，计算出区域内的速度值，并进行分组显示。色标采用绘图色标，保持速度分组的颜色与原始速度模型的颜色一致，如图8所示。

速度编辑时，按如下步骤进行操作：

1)首先选择速度区域，右击图像区域，选择清空菜单。

2)同时会在旁边空白绘图区域里把清空的部分显示出来。如图9所示。

清空之后，右击图像区域，在弹出的菜单中选择插值方法，进行插值。插值方法分别是线性插值、反比权重插值、克里金插值。三种插值方法效果如表1所示。线性插值的光滑度不够，速度值变化趋势不明显。距离反比权重插值的幂次越高，结果精确性越高，但计算量越大。克里金插值不仅考虑样点数据值还考虑周边邻近点的位置以及它们之间的关系，结果更为精确。

4 结论

根据速度分析建立精细、准确速度场的需求，研究了对沿层速度模型速度值进行编辑的插值算法和应用工具，开发了具有加载速度模型数据、绘制层速度模型图像、浏览速度值、速度范围直方图、速度编辑等功能的软件系统，实现了有针对性的去除速度异常值，提高速度精度，为后续地震勘探处理和解释工作取得有效结果提供借鉴。