典型模型瑞雷波椭圆率曲线形态特征分析

2020-12-30殷勇

物探化探计算技术 2020年6期

殷勇

(福建省建筑设计研究院有限公司,福州 350001)

0 引言

地球表面每时每刻都在不停的做无规则的微幅振动，称之为环境振动(ambient vibrations)。它是用于表示由人类活动、交通运输、工业生产、气候变化、海浪、潮汐等诸多因素引起的地面周围振动的通用术语。清楚地对所有振动源进行分类非常困难，Gutenberg[1]根据频率列出了不同类型的振动源；Asten[2]和Henstridge[3]在噪声评估中也得出了相同的结论。分析表明，环境振动基本上有两种不同的起源：自然和人文的，并且频率范围不同。这种差异导致了将环境振动分为微震动(microseisms)和地脉动(microtremors)。分别对应于自然和人文的来源，以及相对较低和较高的频率。通常低频(低于1 Hz)源是自然的(海洋、大尺度气象)；在中频(1 Hz～5 Hz)来源是自然的(当地气象)或人文的(城市)；在更高的频率上，源基本上是人文的。

微动勘探是环境振动在浅层工程勘察领域的专用术语，频率范围主要集中1.0 Hz～50 Hz范围，源主要是人文的，低频段可能有部分是自然的。另外一种利用环境振动进行勘探的是地震背景噪声(Seismic Ambient Noise)层析成像，频率范围主要集中0.01 Hz～1 Hz范围，源主要是自然的。这两种方法所采用的频带范围、数据处理方法、源的来源与特征不同，其物理思想相同。

微动是一种由体波(P波和S波)和面波(瑞雷波和勒夫波)组成的复杂振动，通常情况面波占优势。与体波相比，面波能量主要集中在自由地表附近，以柱面波扩散的形式传播，传播距离远、衰减慢、能量大，易于在地表接收。因此，面波勘探方法被广泛应用于地球结构探测和工程勘察及各种无损检测中。面波在勘察中的应用，主要是利用面波的频散特性，即在均匀水平分层介质中，不同频率成分的面波以不同的传播速度传播。频率越低的成分传播速度受到越深介质属性的影响，频率越高的成分传播速度受到越浅介质属性的影响。计算出不同频率的面波速度(频散曲线)，就可以通过一定的反演方法来推断不同深度介质的属性，从而达到探测的目的。利用面波获得剪切波速度结构是面波勘探的一个主要目的，已被广泛应用。

除了频散曲线，瑞雷面波还有表现出与地层结构直接相关的第二个属性：椭圆率(χ)。该参数表示瑞雷波传播中，质点椭圆极化运动的水平轴和垂直轴之间的比率，此参数也为频率的函数。椭圆率受介质厚度(h)、密度(ρ)、纵波速度(Vp)、横波速度(Vs)、纵波品质因子(Qp)、横波品质因子(Qs)的影响，这些因素中，对椭圆率影响最大的是厚度与横波速度。

目前基于微动记录的H / V技术已经变得越来越流行，这项技术首先由Nogoshi等[14]应用，并由Nakamura[15-17]推广，它是一种方便，实用和低成本的工具，可用于城市化区域。微动H/V技术理论尚不完备，目前主要有两个方向的理论研究：①通过考虑整个环境振动波场来描述H / V曲线;②研究瑞雷波椭圆率。对第一个理论分支，存在两种环境振动波场模型，它们分别为分布式表面源法(DSS)和散射场法(DFA)。

我国对微动H/V技术的应用研究，主要是根据场地卓越周期对观测场地进行分类和震害关系这方面而开展。郭明珠等[5-6]结合微动记录的运动学和动力学特征，提出了判定微动波场性质的形态法、轨迹法和基岩微动谱比法，采用统计的方法研究了微动单点谱比法测定场地动力特性的有效性；陈棋福等[7]利用北京市五环内间距1 km～2 km的600多个点位的微动观测记录，采用H/V谱比法得到了北京城区高分辨的沉积层卓越频率(卓越周期)和放大倍数及沉积盖层厚度分布；王伟君等[8]根据台阵观测技术应用H/V谱比法分析获取了北京市五棵松体育馆的场地响应；彭菲等[9]从正演的角度出发，分别建立了水平层状、倾斜层状和不均匀构造三种由简单到复杂的模型，采用时域有限差分方法(FDTD)模拟微动随机源的探测数据，将数值模拟获得的数据利用H/V谱比法进行反推，得出了与原模型设置值相对比符合良好的结论；杨奎[10]等基于微动面波H/V谱的基本原理，通过对给定模型的数值计算，得到了微动面波的介质响应曲线和H/V谱，分析了面波中瑞雷波和勒夫波多模式波的介质响应和H/V谱特征，结果表明微动面波的介质响应特征与地层界面具有一定的对应关系，且在H/V谱中瑞雷波和勒夫波的主频具有一致性，勒夫波利用对H/V谱具有增强作用。

笔者首先通过水平层状介质中几种典型模型的瑞雷波椭圆率一维数值计算，分析各模型瑞雷波椭圆率曲线特征，然后进一步通过工程实例，分析微动H/V曲线与瑞雷波椭圆率的关系。

1 一维数值计算

1.1 瑞雷波椭圆率一般形态

瑞雷波沿不同分层介质传播，质点振幅随深度衰减，能量主要集中在分层界面附近。在瑞雷波的传播方向上，表层质点运动呈逆时针椭圆形，一定深度后质点运动呈顺时针椭圆形，深度进一步加大质点运动又变回逆时针椭圆形，如此循环，直至能量衰减为零。我们将这种质点方向和振幅随深度不断变化的现象，称为瑞雷波的椭圆极化现象。瑞雷波存在不同模态的椭圆率。图1为表1两层模型A数值计算所得的瑞雷波各模式椭圆率曲线。mode0为基阶模态，mode1-mode4为高阶模态。在实际勘探应用中，瑞雷波多数以基阶波占主导，因此，我们主要讨论瑞雷波的基阶椭圆率。

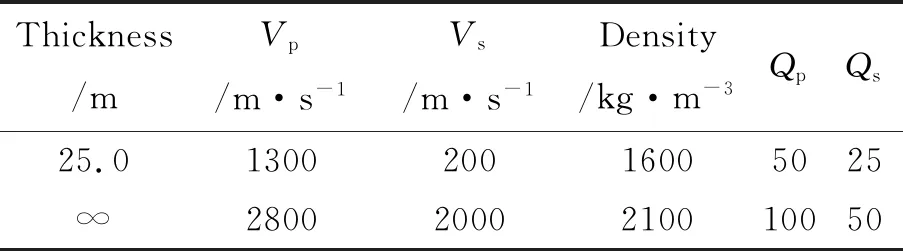
表1 两层模型A

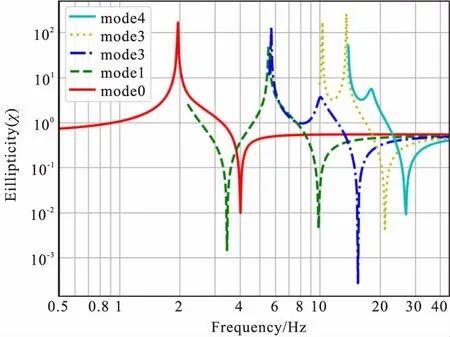
图1 两层模型A瑞雷波多模式椭圆率曲线Fig.1 Rayleigh wave ellipticity curve of two layers model A

在大多数情况下，瑞雷波基阶椭圆率曲线均表现出一些固有的形态，如存在一峰一谷、在峰值频率(fp)处，质点无垂直振动，在谷值频率(fz)、也称零值频率处，质点无水平振动，两者均为椭圆率曲线的奇异点，质点运动方向在奇异点处发生转换。如图2为表1两层模型A瑞雷波基阶椭圆率曲线，fz位于频率4.01 Hz处，fp位于频率1.95 Hz处，从高频至低频，质点运动方向由逆时针-顺时针-逆时针变化。

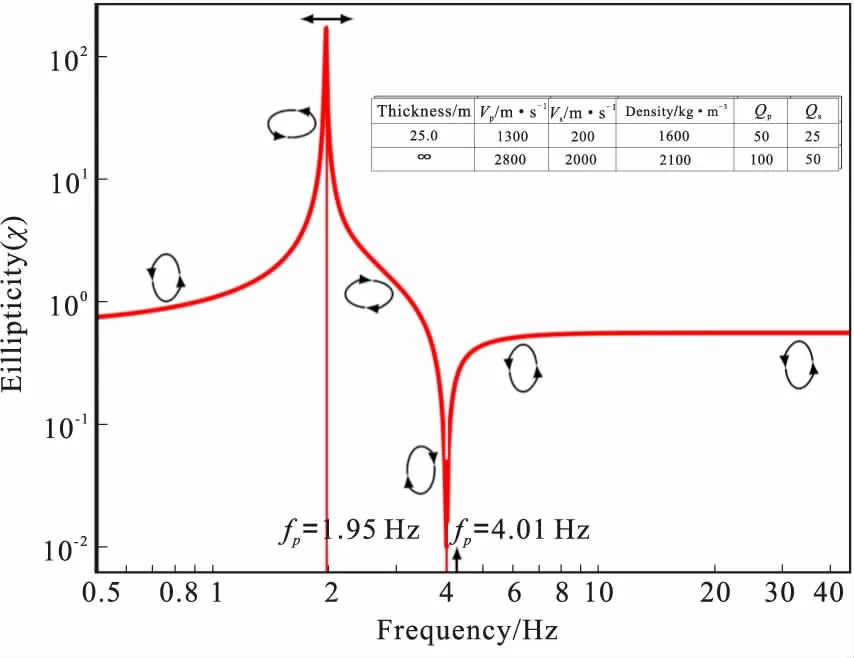
图2 两层模型A瑞雷波基阶椭圆率曲线及质点运动Fig.2 The ellipticity curve and particle motion for the fundamental Rayleigh wave mode in the two layers model A

1.2 数值计算模型系列

为了对应实际浅层勘探工作中遇到各种不同地层情况，采用以下5种地质模型系列来进行数值计算。

1)模型系列A(2层)，此模型系列各层中Vp、Vs、ρ、Qp、Qs参数保持不变，h变化，主要探讨峰值频率(fp)、谷值频率(fz)及两者比(fz/fp)与深度的关系。

2)模型系列B(2层)，此模型系列保持第二层参数及第一层中h、Qp、Qs参数不变，第一层Vs、Vp、ρ变化，主要探讨波速差异较小时，椭圆率曲线的特征。

3)模型系列C(5层)，此模型系列各层Vp、Vs、ρ、Qp、Qs保持不变，各层厚度比例(h1:h2:h3:h4)保持不变，对各层厚度乘不同的比例系数。

4)模型系列D(6层)，此模型系列为含低速夹层模型，模型参数中总厚度(H)、各层Vp、Vs、ρ、Qp、Qs保持不变，h1、h2、h3、h4、h5分别选取其中一个层厚以一定间隔增加至H*80%，其余4层均分剩下的厚度。

5)模型系列E(6层)，此模型系列为含高速夹层模型，模型参数变化与模型系列D相同。

1.3 计算结果

1.3.1 模型系列A(2层)

选用参数Vp1、Vs1、ρ1、Qp1、Qs1分别为: 1 300 m/s, 200 m/s, 1 600 kg/m3, 50, 25;Vp2、Vs2、ρ2、Qp2、Qs2为：2 800 m/s，1 000 m/s, 2 100 kg/m3, 100, 50。h1以5 m为间隔从5 m变化至50 m，第①模型h1为5 m，第⑩模型h1为50 m。

通过数值计算，得到了此模型系列基阶椭圆率曲线(图3)，及各曲线上一些特征点数据(表2)。图3表明各模型椭圆率曲线表现为单峰单谷，形态大致相同，表2数据可以分析出，谷值频率(fz)、峰值频率(fp)均随h1厚度增大而减小，且满足幂指数关系。其中fp=48.82h1-1.001；fz=100.22h1-1.001；fz/fp为固定值2.053与h1厚度无关。其中fp与h1关系转换成传统fp=(4*Vs)/H形式，可求得Vs=48.82*4=195.28 m/s，与第一层剪切波速200 m/s有近2.36%差异。如采用fz=(2*Vs)/H形式，求得Vs=100.22*2=200.44 m/s，与第一层剪切波速差异仅0.22%。

图3 模型系列A基阶椭圆率曲线Fig.3 The ellipticity curves for the fundamental Rayleigh wave mode in the series of two layers model A

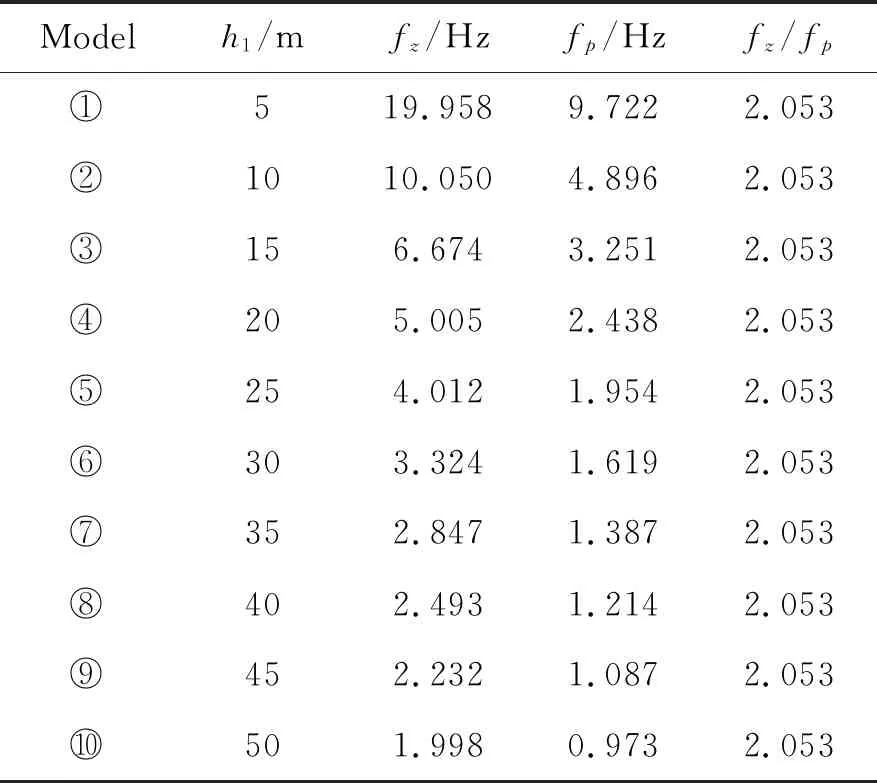
表2 模型系列A基阶椭圆率曲线特征点数据

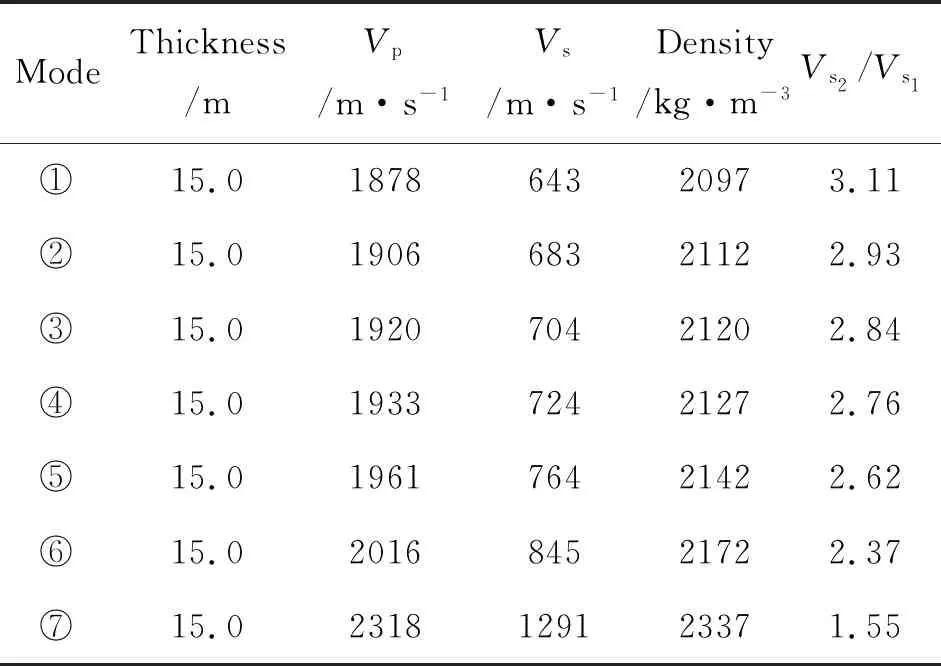
表3 模型系列B曲线剧烈变化位置模型参数

图4 模型系列B曲线剧烈变化位置基阶椭圆率曲线Fig.4 The drastically varied ellipticity curves for the fundamental Rayleigh wave mode in the model B series

1.3.2 模型系列B(2层)

保持第二层参数及第一层中h1、Qp1、Qs1参数不变，其中Vp2、Vs2、ρ2、Qp2、Qs2取值为：2 800 m/s，2 000 m/s, 2 600 kg/m3, 100, 50；h1、Qp1、Qs1取值为：15 m、50 m、25 m。第一层Vs1按间隔约20 m/s由400 m/s变化至2 000 m/s，分为78个模型，Vp1、ρ1随Vs1变化按一定取值进行变化。

通过数值计算，当Vs1从400 m/s变化至704 m/s，各模型椭圆率曲线均表现为单峰单谷，形态大致相同，谷值频率(fz)由13.25 Hz增至20.86 Hz；峰值频率(fp) 由6.46 Hz增至17.48 Hz；fz/fp由2.053减至1.194。峰谷值频率及fz/fp值变化范围均较大。

表4 模型系列C地层参数表

在这一系列模型中，椭圆率曲线由单峰单谷形态变化至近水平直线，我们挑选出了曲线剧烈变化的七个模型(表3)，并绘制出了这七个模型的基阶椭圆率曲线图(图4)。图4表明①模型、②模型、③模型表现为单峰单谷形态，Vs2/Vs1在2.84～3.11之间；④模型表现为单小缓峰及两个零值点，Vs2/Vs1为2.76；⑤模型、⑥模型表现为单小缓峰及单小缓谷，Vs2/Vs1在2.37～2.62之间；⑦模型近水平直线，Vs2/Vs1为1.55。

剪切波速差异的大小Vs2/Vs1直接影响着椭圆率曲线的形态，当Vs2/Vs1小于2.37时曲线表现近似水平直线；当Vs2/Vs1在2.37～2.76时曲线表现小缓峰及小缓谷，个别模型会突变为小缓峰及两个零值点；当Vs2/Vs1大于2.76时，曲线表现单峰单谷，随着Vs2/Vs1增大fz/fp逐渐增大，最后稳定在一个最大值。

表5 模型系列C不同等效速度对比

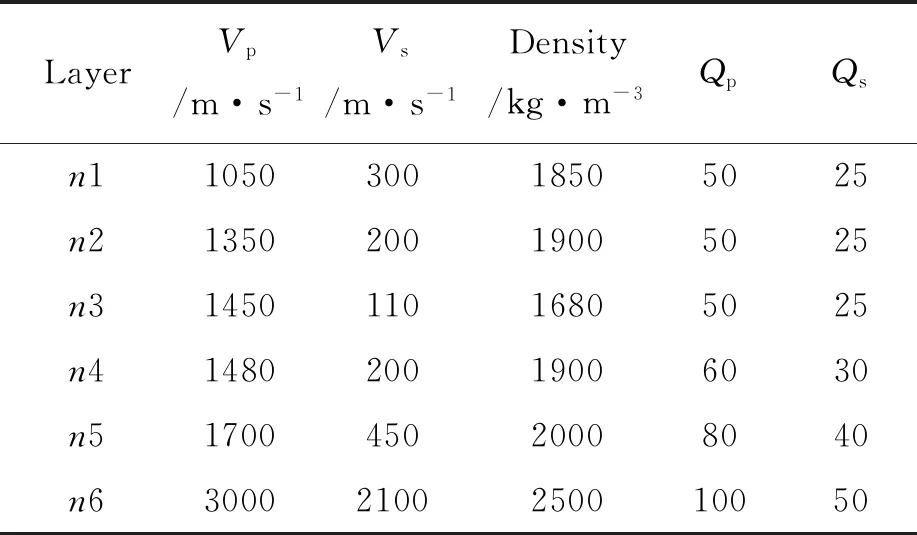
表6 模型系列D地层参数表

1.3.3 模型系列C(5层)

各层Vp、Vs、ρ、Qp、Qs保持不变，各层厚度比例(h1:h2:h3:h4)保持不变，对各层厚度乘不同的比例系数。实际数值计算时各层Vp、Vs、ρ、Qp、Qs采用了表4中的参数，(h1:h2:h3:h4)分别计算了(1.0:0.5:1.0:0.5)、(1.0:0.8:0.6:0.4)、(1.0:1.0:1.0:1.0)、(1.0:1.5:2.0:2.5)四种厚度比例关系。

各层厚度比例系数以0.5 m为间隔从1.0 m至20.0 m，每组共计39个模型。通过数据计算，四组比例关系fp、fz与总厚度h(h1+h2+h3+h4)均满足幂指数关系。厚度比例为(1.0:0.5:1.0:0.5)时，fp=83.109h-0.999，fz= 202.4h-1.002，fz/fp为固定值2.430；厚度比例为(1.0:0.8:0.6:0.4)时fp=75.63h-0.998，fz=182.56h-0.997，fz/fp为固定值2.430；厚度比例为(1.0:1.0:1.0:1.0)时fp=93.985h-0.998，fz=254.53h-0.998，fz/fp为固定值2.715；厚度比例为(1.0:1.5:2.0:2.5)时fp=118.93h-1.001，fz= 431.41h-1.002，fz/fp为固定值3.583。随着n3、n4层权重占比的增大，fz/fp也随之增大。如果我们将fp与h关系转换成传统fp=(4*Vs)/H形式，将fz与h关系转换成传统fz=(2*Vs)/H形式，可求得四种不同比例的等效速度Vs值、与基于时间的等效速度和基于厚度等效波速对比(表5)。

从表5中可以看出，无论是利用fp求取的等效速度，还是利用fz求取的等效速度，均与基于时间和基于厚度的等效波速有较大差异。不能相互替换使用。实际fp和fz均是的函数，其中h，Vs对fp、fz影响较大，而Vp、ρ、Qp、Qs对fp、fz影响较小。

由于瑞雷波椭圆率曲线中fp、fz是重要的特征数据，建立fp、fz与h的关系也是实际应用所期待的。工程应用时，我们可以利用测区内部分钻孔的地层模型，得到不同厚度比例地层的幂指数关系，通过分析场地的地层特征，得出具有与场地地层特征相关的fp、fz与h的近似关系式。

1.3.4 模型系列D(6层)

为含低速夹层模型，模型参数中总厚度(H=50 m)、各层Vp、Vs、ρ、Qp、Qs保持不变，各层厚度(h)以一定间隔变化至总厚度的80%，剩余厚度由其它各层均分。数值计算时各层Vp、Vs、ρ、Qp、Qs采用了表6中的参数，各层厚度(h)变化间隔为1.33 m。

n1层厚度从1.33 m变化至40.0 m时，基阶椭圆率曲线均为单峰单谷形态，fp呈先递减后递增趋势，由0.91 Hz递减至0.87 Hz再增至1.06 Hz；fz呈递增趋势,由2.03 Hz增至2.58 Hz；fz/fp先递增后递减，由2.24增至2.57再递减至2.42。fp、fz变化范围较小。

n2层厚度从1.33 m变化至40.0 m时，基阶椭圆率曲线均为单峰单谷形态，fp呈先递减后递增趋势，由0.95 Hz递减至0.84 Hz再增至0.87 Hz；fp呈递减趋势，由2.16 Hz减至1.96 Hz；fz/fp先增后减，由2.28递增至2.37再递减至2.24。fp、fz变化范围较小。

n3层为低速层，厚度从1.33 m变化至40.0 m时，基阶椭圆率曲线均为单峰单谷形态，fp、fz均呈递减趋势，fp由1.15 Hz递减至0.58 Hz；fz由2.53 Hz递减至1.20 Hz；fz/fp先增后减，由2.20递增至2.33再递减至2.07。fp、fz变化范围较大。

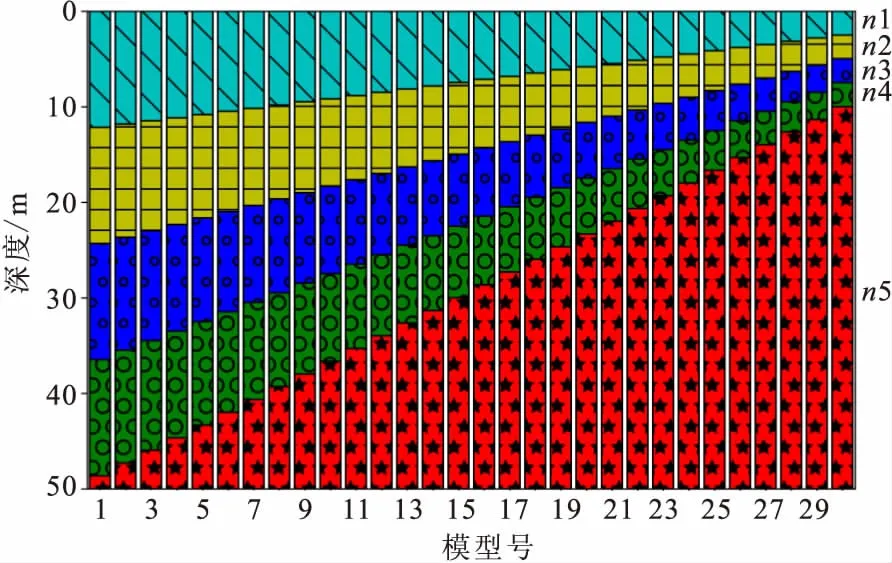
图5 模型系列D中n5变化模型堆叠图Fig.5 The stacked bar of the model D series with layer 5th varied

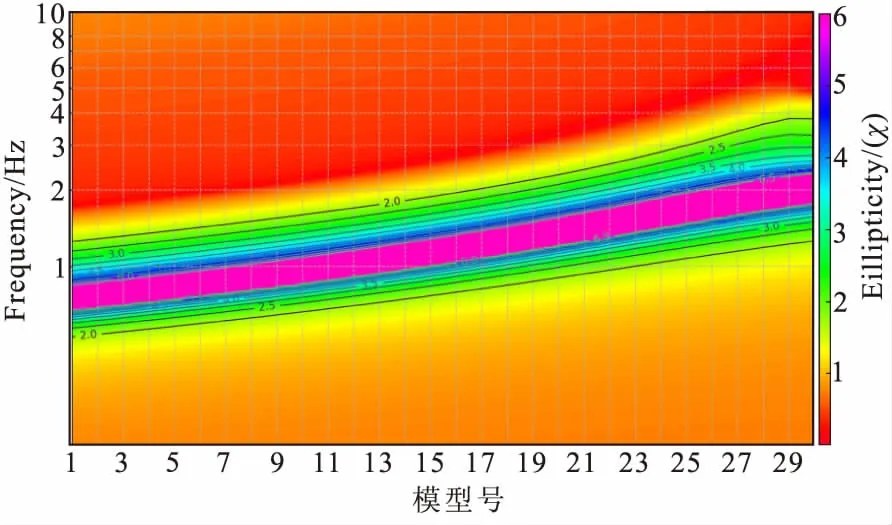
图6 模型系列D中n5变化模型基阶椭圆率等值线图Fig.6 The contour of ellipticity curves for the fundamental Rayleigh wave mode in the model D series with layer 5th varied

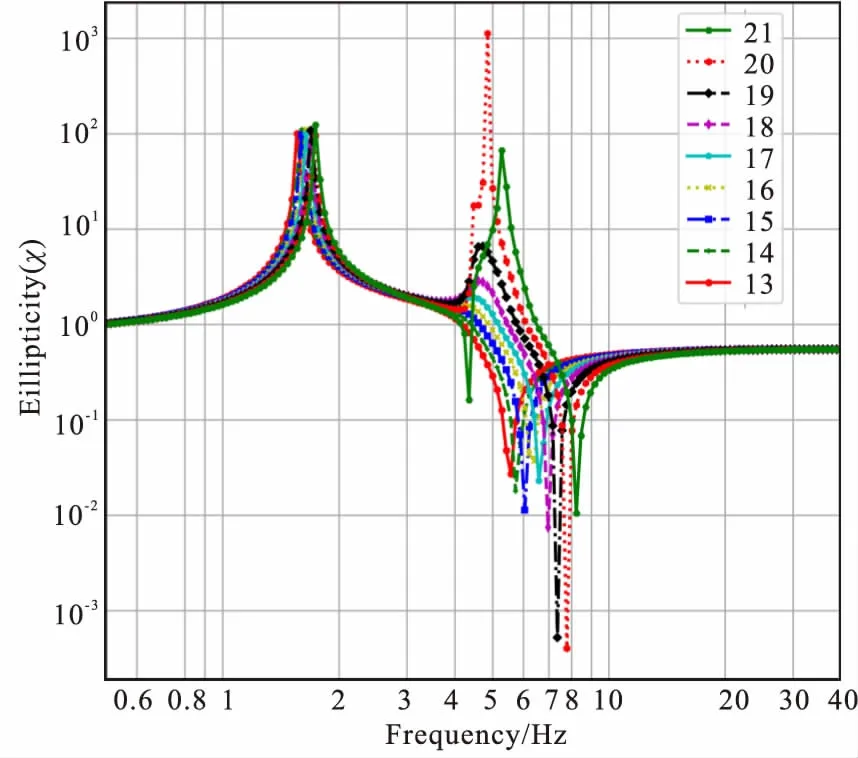
图7 模型系列D中n5变化28-30模型基阶椭圆率曲线Fig.7 The ellipticity curves for the fundamental Rayleigh wave mode in the model D series(28-30) with layer 5th varied

表7 模型系列E地层参数表

n4层厚度从1.33 m变化至40.0 m时，基阶椭圆率曲线均为单峰单谷形态，fp呈先递增后递减趋势，由0.81 Hz递增至1.00 Hz再递减至0.98；fz也呈先递增后递减趋势，由1.96 Hz递增至2.20 Hz再递减至2.12 Hz；fz/fp呈递减趋势，由2.47递减至2.15。fp、fz变化范围较小。

n5层厚度从1.33 m变化至37.33 m时(图5中1-28模型)，基阶椭圆率曲线均为单峰单谷形态，fp、fp、fz/fp均呈递增趋势，fp由0.73 Hz递增至1.88 Hz；fz由1.74 Hz递增至6.00 Hz；fz/fp由2.37递增至3.19，fp、fz变化范围较大。30模型(图6)表现出3个零值点。

含低速夹层模型中，半无限空间上覆地层中低速夹层的速度、上覆地层中高速度地层的厚度显著地影响着fp和fz的大小。大多数情况基阶椭圆率曲线均表现为单峰单谷形态，在某些特定模型中，有多个零值点出现。

1.3.5 模型系列E(6层)

为含高速夹层模型，模型参数中总厚度(H=50 m)、各层Vp、Vs、ρ、Qp、Qs保持不变，各层厚度(h)以一定间隔变化至总厚度的80%，剩余厚度由其他各层均分。数值计算时各层Vp、Vs、ρ、Qp、Qs采用了表7中的参数，各层厚度(h)变化间隔为1.33 m。

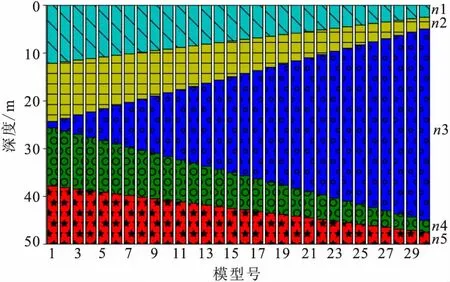
图8 模型系列E中n3变化模型堆叠图Fig.8 The stacked bar of the model E series with layer 3rd varied

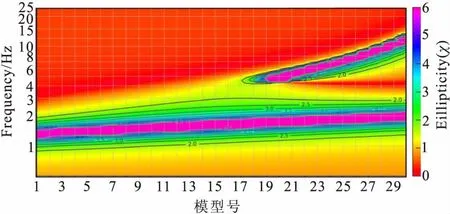
图9 模型系列E中n3变化模型基阶椭圆率等值线图Fig.9 The contour of ellipticity curves for the funda-mental Rayleigh wave mode in the model E series with layer 3rd varied

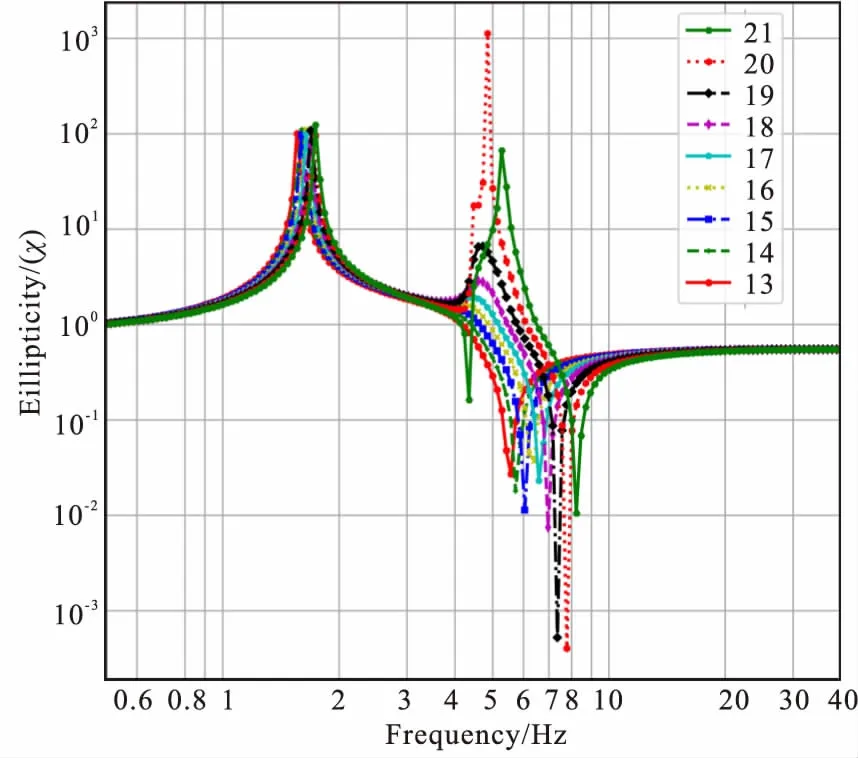
图10 模型系列E中n3变化13-21模型基阶椭圆率曲线Fig.10 The ellipticity curves for the fundamental Rayleigh wave mode in the model E series(13-21) with layer 3rd varied

n1层厚度从1.33 m变化至40.0 m时，基阶椭圆率曲线均为单峰单谷形态，fp呈递减趋势，由1.60 Hz递减至0.85 Hz；fz呈先递增后递减趋势，由4.00 Hz递增至4.47 Hz再递减至1.79；fz/fp先递增后递减，由2.50增至3.03再递减至2.12。模型中高速层占比相对较大时，fz/fp相对较大。

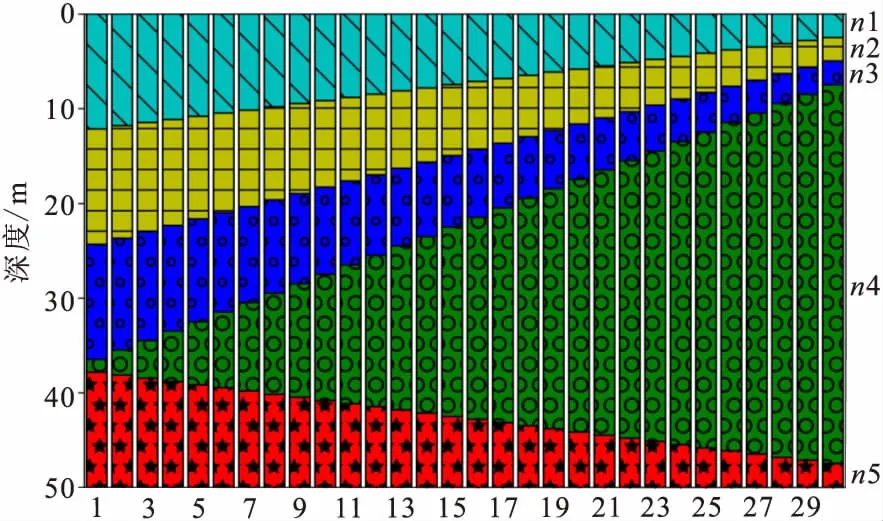
图11 模型系列E中n4变化模型堆叠图Fig.11 The stacked bar of the model E series with layer 4th varied

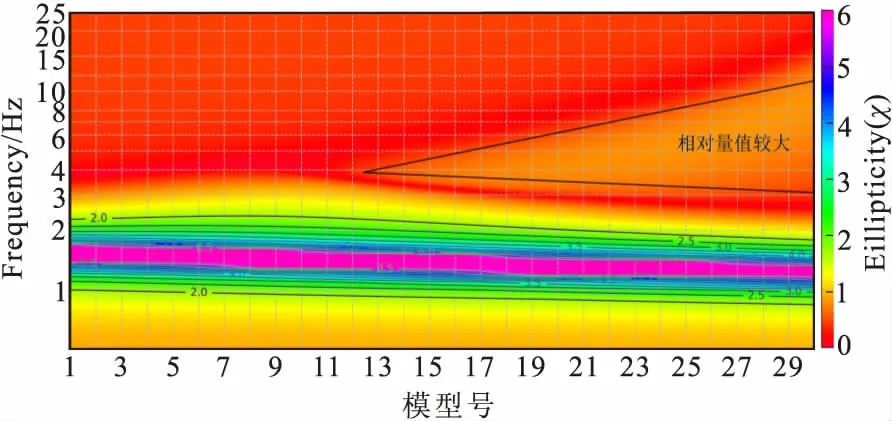
图12 模型系列E中n4变化模型基阶椭圆率等值线图Fig.12 The contour of ellipticity curves for the funda-mental Rayleigh wave mode in the model e series with layer 4th varied

n2层厚度从1.33 m变化至40.0 m时，基阶椭圆率曲线均为单峰单谷形态，fp、fz、fz/fp均呈递减趋势，fp由1.56 Hz递减至1.06 Hz；fz由5.43 Hz递减至2.24 Hz；fz/fp由3.49递减至2.12。模型中高速层占比相对较大时，fz/fp相对较大。

n3层为高速层，厚度从1.33 m变化至40.0 m时，共分为30个模型(图8)。

通过数值计算，基阶椭圆率曲线形态有较大变化，1-13模型表现单峰单谷，20-30模型表现为两组频率轴上分离的单峰单谷形态，14-19模型为两者的过渡变化形态。从图9系列模型基阶椭圆率等值线图中，可以清晰地观察出椭圆率曲线形态在量值上的变化，图10中可清晰观察13-21模型过渡形态曲线变化。

形成两组单峰单谷形态除了要求n3高速层与上覆地层的波速差异要较大外，n3高速层的厚度需要大于某一临界值。本模型系列n3厚度需大于25.33 m。

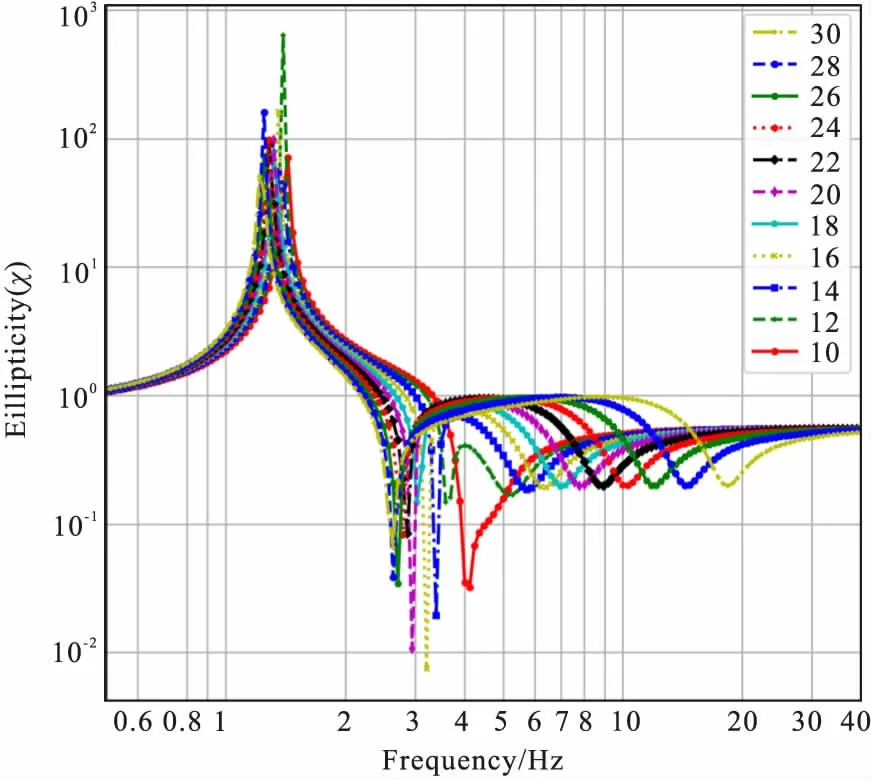
图13 模型系列E中n4变化10-30模型基阶椭圆率曲线Fig.13 The ellipticity curves for the fundamental Ray-leigh wave mode in the model E series(10-30) with layer 4th varied

n4层厚度从1.33 m变化至40.0 m时，fp呈递减趋势，由1.52 Hz递减至1.21 Hz，变化量较小；fz、fz/fp均呈先递增后递减趋势，fz由3.79 Hz递增至4.35 Hz再递减至2.64 Hz；fz/fp由2.50递增至3.03 再递减至2.12；1-11模型(图11)椭圆率曲线为单峰单谷形态，12-30模型在高频段有相对量值较大区段(图12)，并且区段影响逐渐扩大。12-30模型中n3高速体埋深逐渐变浅，厚度逐渐变小。图13中可清晰观察10-30模型的曲线变化情况。

含高速夹层模型中，高速层的速度、厚度均显著地影响着椭圆率曲线形态，高速夹层与上覆地层波速差异较大且具有一定厚度是产生两组频率轴上分离的单峰单谷形态的必需条件。

2 应用实例

微动由面波与各种体波共同组成，各种地震波的比例影响着微动H/V曲线的形态，通过微动H/V谱与瑞雷波基阶椭圆率进行对比分析，说明瑞雷波椭圆率对解释微动H/V的重要作用。我们选择了3个有代表性的场地共6个钻孔进行了微动测试，每个场地具有不同的地质环境。测试观测系统采用圆形台阵，台阵由六台地震仪组成，位于钻孔中心位置处放置一台(S1)，其余五台(S2～S6)均匀放置在同一圆周上，台阵中心点到圆周的观测半径R取值1.5 m～3.0 m。微动数据采集采用了用宽频带地震仪，对各台仪器进行了一致性测试，各台阵采用无线连接方式，通过GPS授时功能实现各台地震仪信号同步，采集每次观测时长约为15 min～20 min。这种观测方式可以最大限度的利用微动测试数据，可计算钻孔处瑞雷波频散曲线，进一步利用钻孔资料反演地层剪切波速。

目前求取微动H/V曲线有好几种算法，基于时频分析的HVTFA法,基于随机递减技术的RayDEC法[11]和基于极化度的DOP-E[12]技术等。采用传统的谱比法求取。微动不同地震波的成分，微动H/V谱比法(HVSR)法由Nakamura提出，数据采集时仅用单个三分量拾震器实测微动信号，计算水平分量和垂直分量的频谱比值，频率为ω的微动H/V谱可定义为式(1)。

(1)

式中：PNS(ω)和PEW(ω)为两个相互正交的水平运动傅立叶功率谱;PUD(ω)为垂直运动的傅立叶功率谱。而频率ω为的X向运动的傅立叶功率谱P(ω)可表示为式(2)。

(2)

式中:L为不相重叠的数据段的总数;SXl(ω)为X向运动第l个数据段的傅立叶变换。

2.1 实例一

测试地点位于福建省南平市建阳区滨江东路，场地西侧距崇阳溪约200 m，地势平坦，场地地貌为河流冲洪积平原地貌，场地岩土层主要为：①杂填土；②中砂；③碎卵石ⓐ；④碎卵石ⓑ；⑤砂土状强风化石英片岩；⑥碎块状强风化石英片岩；⑦中等风化石英片岩。场地地层起伏变化较小。通过对钻孔A15#、A88#微动测试，我们建立了孔位处地层模型，具体模型中各地层参数见表8、表9。模型中Vs是通过微动面波频散曲线反演获得，Vp和ρ是参照整个场地地层性质由经验给出。通过1D正演数值计算，得到了A15#、A88#孔试验H/V曲线、瑞雷波基阶椭圆率曲线和SH波传递函数对比图(图14(b)，图15(b))。其中计算SH波传递函数是为了分析微动H/V曲线中体波(SH)的影响情况。(图14(a)，图15(a))为测试3个分量信号的振幅谱。

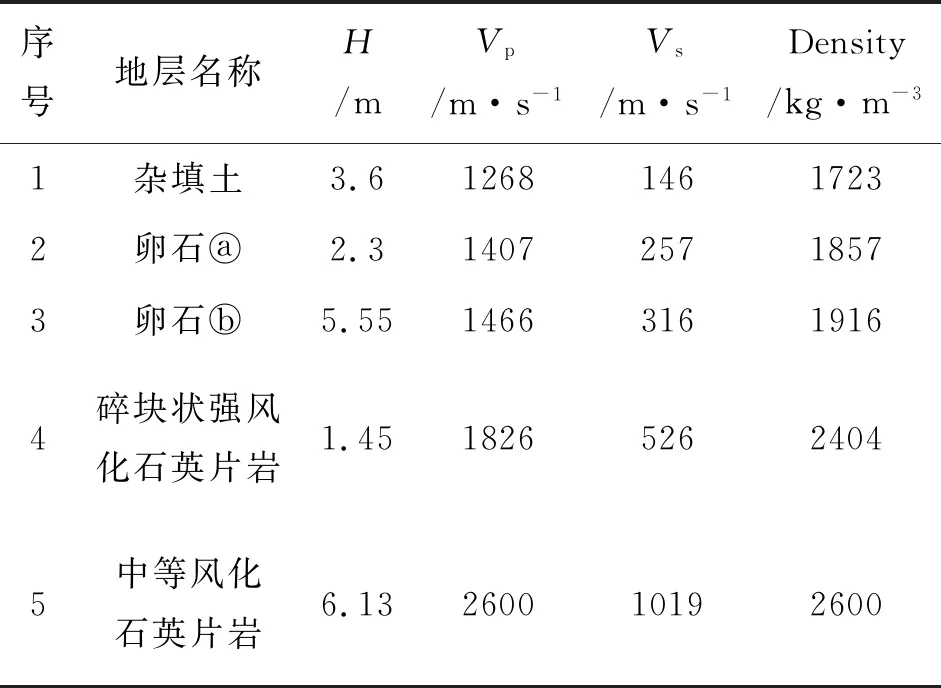
表8 A15#地层模型参数表

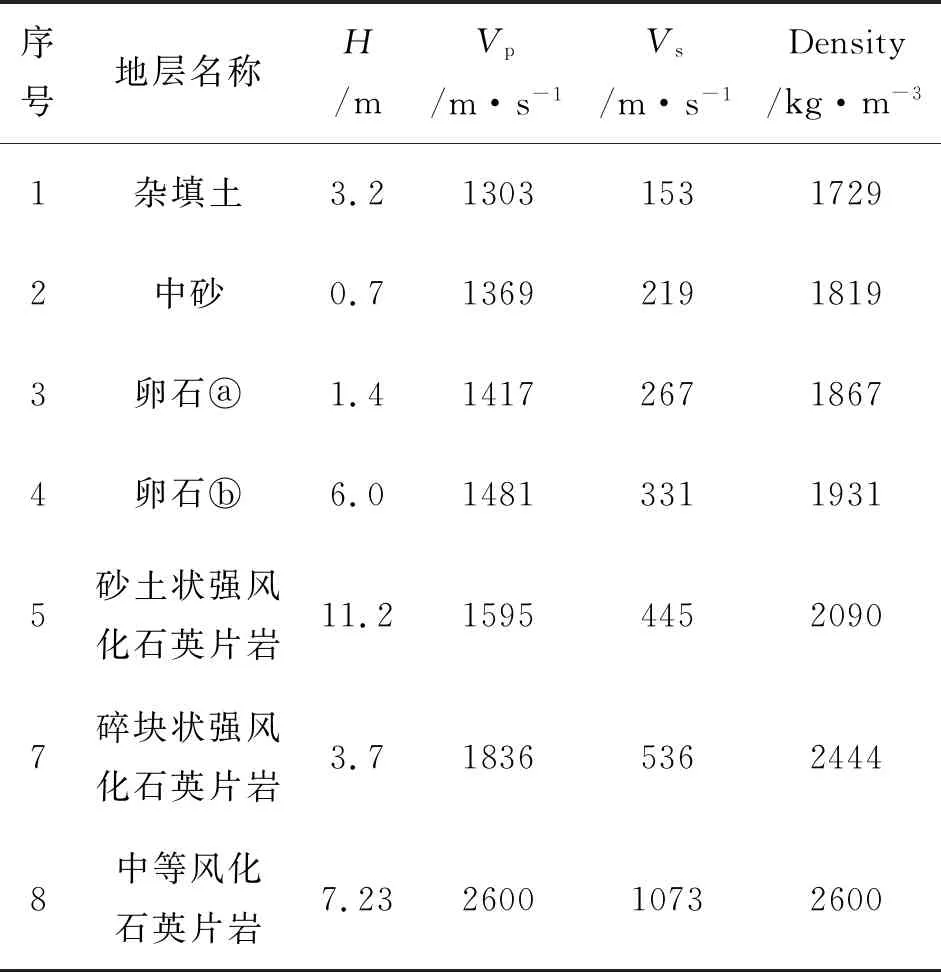
表9 A88#地层模型参数表

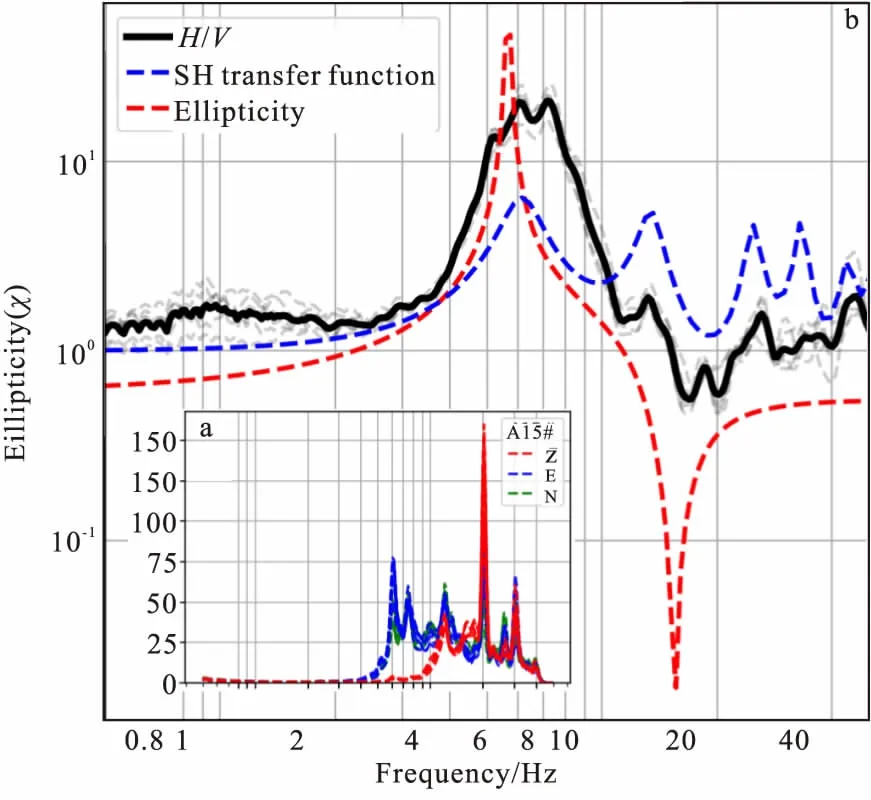
图14 A15# 椭圆率-SH波传递函数-H/V曲线对比图Fig.14 A15# the comparison of the ellipticity curve, SH transfer function and H/V curve(a)三分量振幅谱;(b)基阶椭圆率-SH波传递函数-H/V曲线

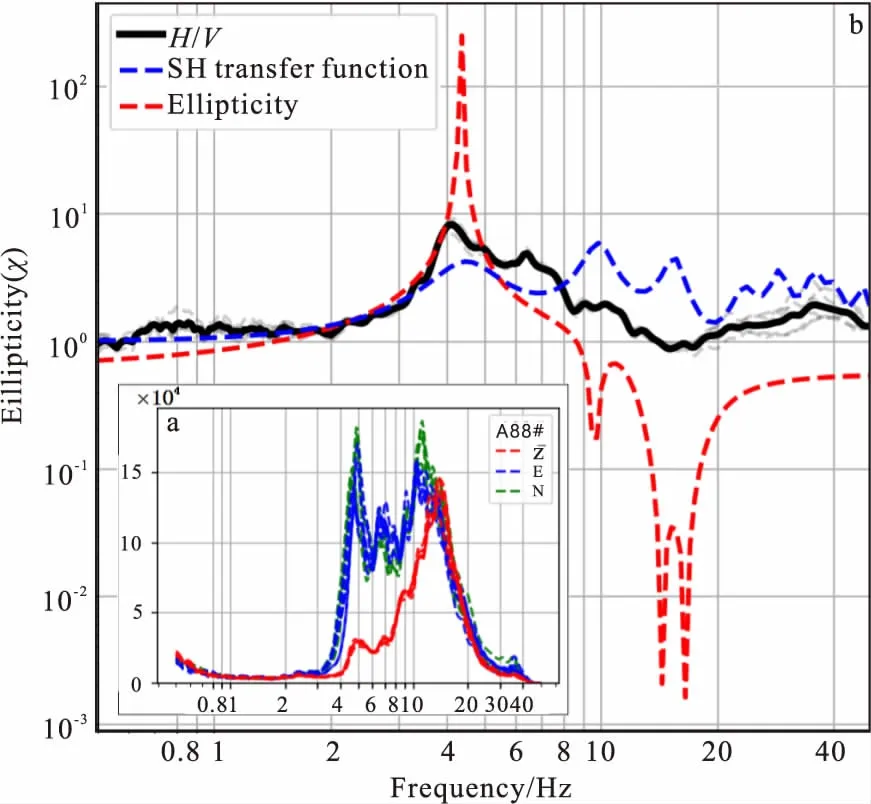
图15 A88# 椭圆率-SH波传递函数-H/V曲线对比图Fig.15 A88# the comparison of the ellipticity curve, SH transfer function and H/V curve(a)三分量振幅谱;(b)基阶椭圆率-SH波传递函数-H/V曲线

图14(b)、图15(b)表明椭圆率曲线与H/V曲线形态有较好的相似性。椭圆率峰值频率、零值频率位置与H/V曲线谐振频率、谷值频率有近似对应关系；SH波传递函数曲线与H/V曲线形态相似性较差，SH波传递函数峰值频率与H/V曲线谐振频率有近似对应关系。

图14(a)、图15(a)表明，微动能量主要集中于H/V谐振频率以上，峰形态所处频率水平分量能量大于垂直分量，显著地影响着H/V峰的形态。

椭圆率曲线与H/V曲线形态很相似，但峰的形态频段宽度及量值上均小于H/V曲线。我们认为H/V曲线峰谷形态是由瑞雷波、Love波、SH波和P波共同谐振形成，在以上2个模型中，SH波传递函数与H/V曲线拟合度较高。因此可以认为，瑞雷波椭圆率曲线与H/V曲线形态差异主要由Love波影响。

2.2 实例二

测试地点位于福建省罗源县中北部，为剥蚀残山地貌，场地位于山间盆谷和河谷平原区，上部由淤泥、淤泥质土、含淤泥粗砂、碎卵石等冲积、洪积层组成，下部由花岗岩及风化层组成。

对钻孔B11#、B20#进行了微动测试，建立了孔位地层模型，具体模型中各地层参数见(表10、表11)，这两个模型均为含低速软弱层模型。通过1D正演数值计算，得到了B11#、B20#孔试验H/V曲线、瑞雷波基阶椭圆率曲线和SH波传递函数对比图(图16、图17)。

表10 B11#测试点地层模型参数表

表11 B20#测试点地层模型参数表

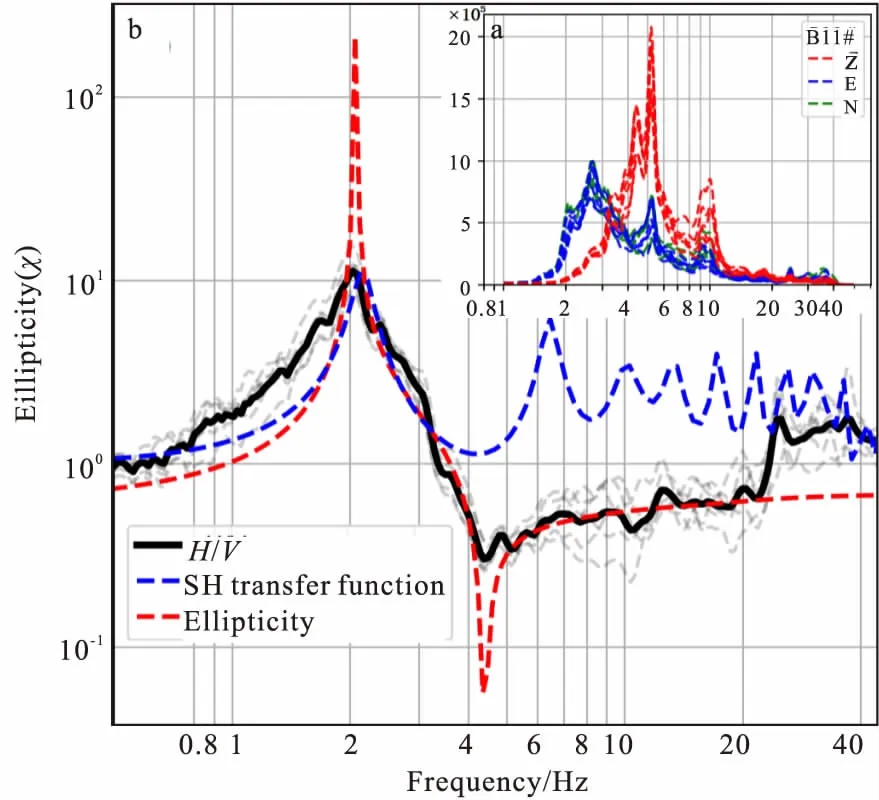
图16 B11# 椭圆率-SH波传递函数-H/V曲线对比图Fig.16 B11# the comparison of the ellipticity curve, SH transfer function and H/V curve(a)三分量振幅谱;(b)基阶椭圆率-SH波传递函数-H/V曲线

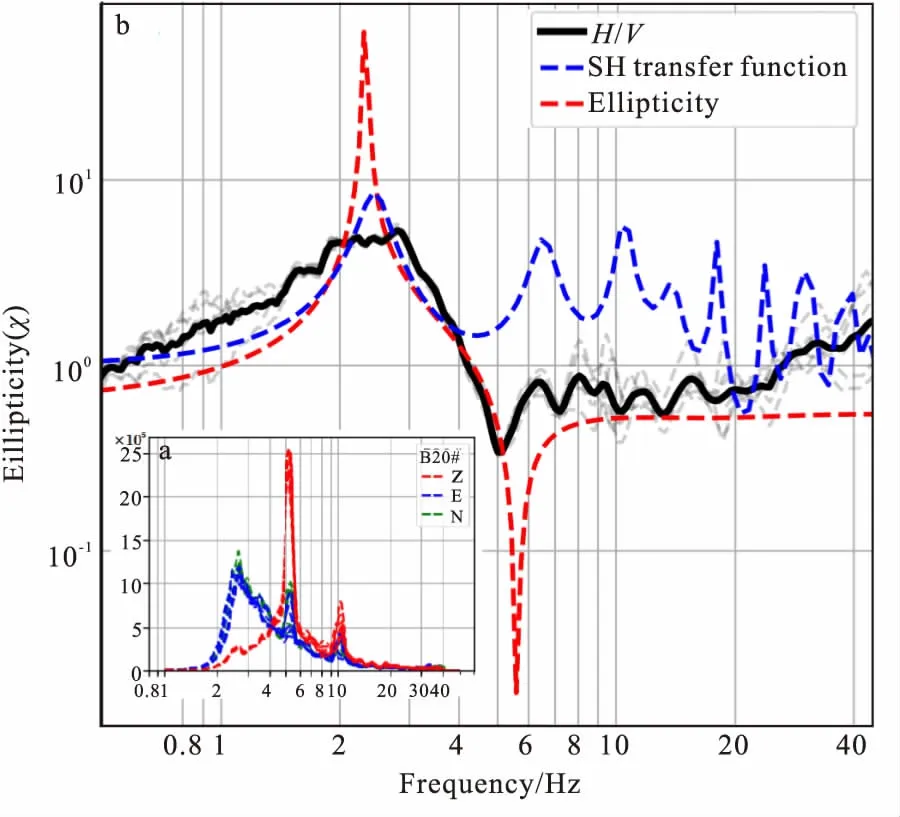
图17 B20# 椭圆率-SH波传递函数-H/V曲线对比图Fig.17 B20# the comparison of the ellipticity curve, SH transfer function and H/V curve(a)三分量振幅谱;(b)基阶椭圆率-SH波传递函数-H/V曲线

图16(b)、图17(b)表明椭圆率曲线与H/V曲线形态拟合度非常高，这两个模型实例中H/V曲线形态完全受瑞雷波控制。

2.3 实例三

测试地点位于福建省福清市宏路街道，场地南侧为龙江，为剥蚀残山地貌，地层主要由凝灰岩及风化层组成。我们对钻孔C32#、C139#进行了微动测试，建立了孔位地层模型，具体模型中各地层参数见(表12、表13)。通过1D正演数值计算，得到了C32#、C139#试验H/V曲线、瑞雷波基阶椭圆率曲线和SH波传递函数对比图(图18、图19)。

图18(b)表明椭圆率曲线与H/V曲线形态拟合度非常高，微动H/V曲线形态完全受瑞雷波控制。图19(b)微动H/V曲线近乎水平，与椭圆率曲线拟合程度较差，图19(a)中水平向振幅谱主峰与垂直向振幅谱主峰分离明显，推测C139#孔微动H/V曲线受Love波影响较大。

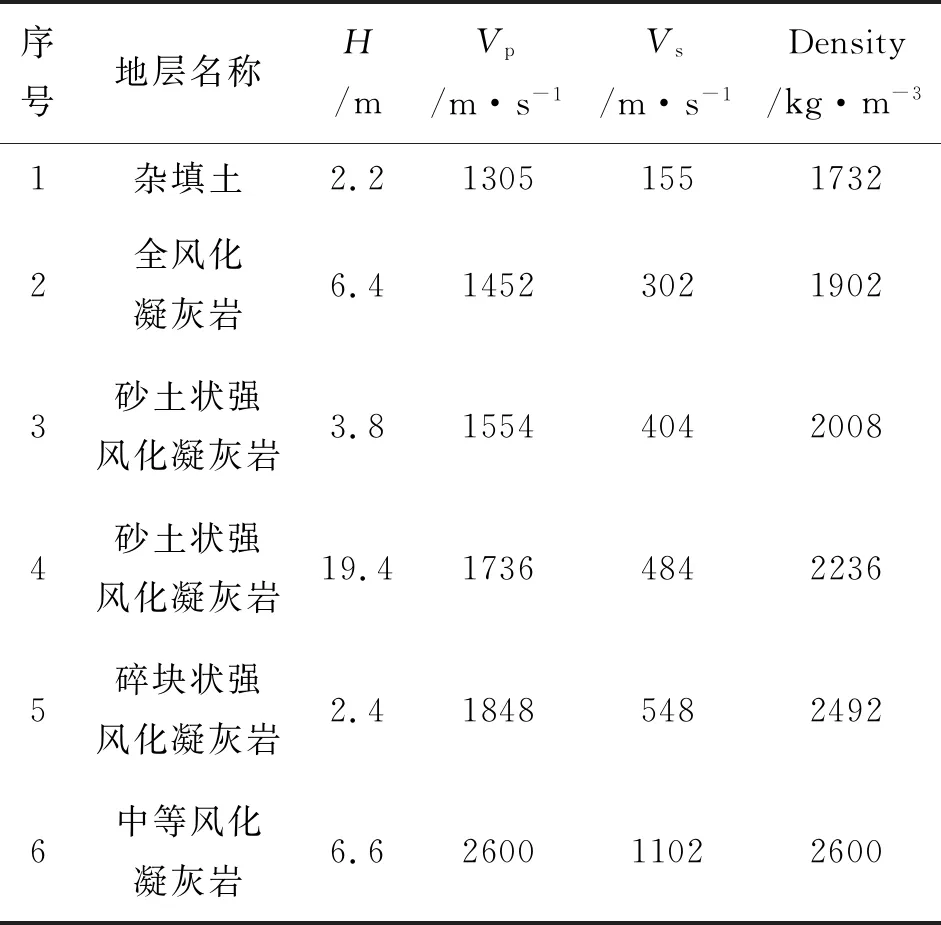
表12 C32#测试点地层模型参数表

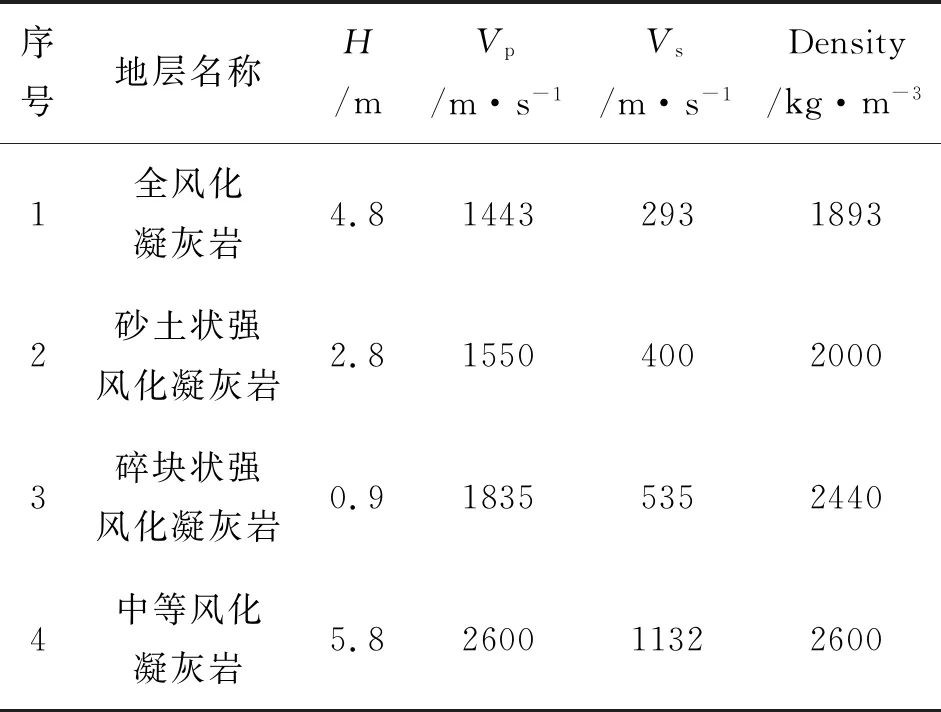
表13 C139#测试点地层模型参数表

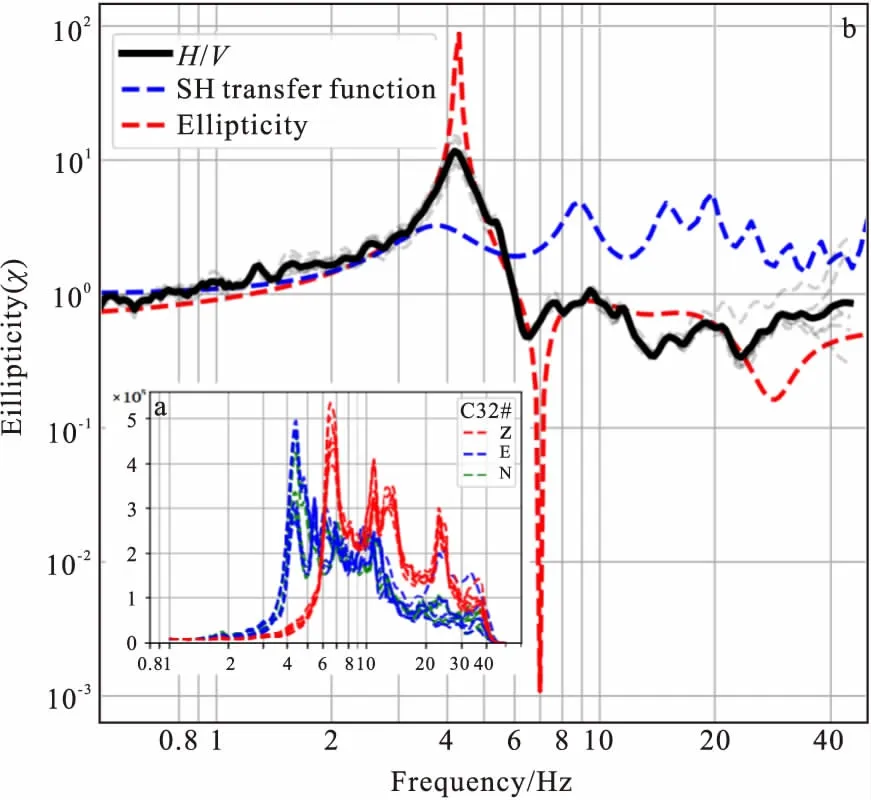
图18 C32# 椭圆率-SH波传递函数-H/V曲线对比图Fig.18 C32# the comparison of the ellipticity curve, SH transfer function and H/V curve(a)三分量振幅谱;(b)基阶椭圆率-SH波传递函数-H/V曲线

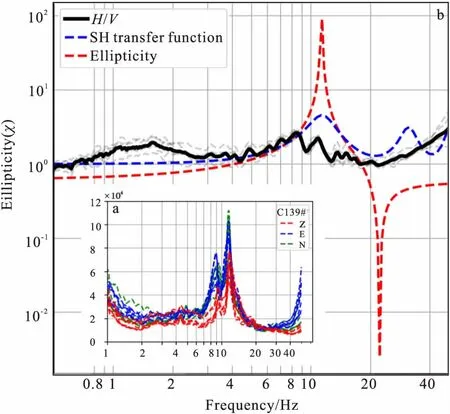
图19 C139# 椭圆率-SH波传递函数-H/V曲线对比图Fig.19 C139# the comparison of the ellipticity curve, SH transfer function and H/V curve(a)三分量振幅谱;(b)基阶椭圆率-SH波传递函数-H/V曲线