浅谈数学线性规划在企业管理中的应用

张博

【摘 要】线性规划是运筹学的分支，近几年来普遍应用在企业管理中，为企业控制成本、提升经济效益做出了重要的贡献。文章主要针对企业管理对数学线性规划的需求及数学线性规划在企业管理中的具体应用进行研究。

【关键词】线性规划;企业管理;利益最大化

【中图分类号】F270 【文献标识码】A 【文章编号】1674-0688（2020）11-0213-03

线性规划能够辅助人们进行高质量的科学管理，主要是针对线性约束条件下线性目标函数的极值问题进行分析。当前，线性规划已经普遍应用于企业管理、经济决策、军事作战等领域，为准确且高效率地利用有限的资源做出了决策依据。在企业管理活动中，线性规划可以用于投资计划、生产计划、运输规划及技术应用等方面，从不同限制的条件组合中选择出最高效、最合理的计算方式，通过建立线性规划模型得出最理想的结果。

1 数学线性规划及其发展

线性规划属于运筹学范围，是运筹学中起步研究时间较早、已经普及应用、应用领域广泛的一个重要分支。1938年苏联列宁格勒大学教授康托洛维奇首次提出线性规划，40年后美国教授又发现了一种计算机线性规划模型的方式——单纯形法。在此之后，经济学家库普曼斯呼吁大家投入线性规划的研究，一批年轻的经济学家、数学家，如胡尔维茨、萨米奥尔逊等都对线性规划展现出极大的兴趣[1]。1975年康托洛维奇与库普曼斯因“最优资源配置理论的贡献”获得了诺贝尔经济学奖。当前，在运筹学众多分支中，线性规划研究最深入、应用最广泛。在单纯形法出现后，可以凭借纸笔进行简单的线性规划模型计算，但是对于规模较大的线性规划模型来说，人工计算难度较大，也极易出现错漏。从实际生产、管理中提出了一系列实际问题，决策变量与约束条件往往达到几十、上百、成千上万个，所以无法使用人力对线性规划模型进行计算。伴随着近年来计算机技术的普及，先后出现了各类解决线性规划模型的软件，并成为企业管理的重要工具。

2 企业管理对数学线性规划的需求

企业日常经营管理中时常会面临着如何使得销售成本最低、利润最高，如何规划最高效、最快捷的路线，以及如何实现最高效率的流动资金周转等一系列问题。针对这些经营管理中的不同问题，可以从不同角度提出各类解决问题的方法。其中，线性规划就是解决这一问题的重要手段。线性规划是一种数学方法，是将数学引入企业管理工作中的重要途径，能够推动现代企业经营管理实现科学化发展。线性规划是数学运筹学的重要分支，主要研究如何利用有限的资源实现最大的价值，或如何利用最少的资源完成既定的工作任务。企业在日常经营管理中需要注重“质”与“量”，以形成统一的整体[2]，企业所进行的经济活动也需要达成“质”与“量”的平衡。企业在经营管理中进行决策、预测及制订计划都需要进行定量的分析与对比，通过计算选择最合理的管理方案，经过数学模型选择最合理的决策、计划。企业日常经营中存在人力、财力、物力等方面的运用，要实现它们相互关系的平衡就需要实现数与量的平衡。应用线性规划则能够在数量上为企业提供可行性强的计划与方案。通过线性规划，可以在若干个可供选择的方案中选取最好的方案。线性规划在企业管理中具有普遍适用性，因此它已经在企业管理中得到了普及应用，尤其是随着计算机技术的成熟发展，解决了线性规划计算繁杂的问题。近几年，伴随着企业管理的科学化，线性规划已经被越来越多的企业管理者重视，日益成为企业规划方案、科学决策的重要工具。

3 线性规划的数学模式

线性规划是在满足相应约束条件下用最少的资源达到目标经济效益。从企业管理角度来看，要想提升企业经济效益可以从两个方面入手：一是升级优化技术，例如引入先进设备、增加设备数量、挖掘资源潜力等;二是在企业设备资源等硬件环境保持不变的情况下，通过转变企业的经验管理方案与计划提升企业经济效益。线性规划就是在企业资源不变的情况下用于调整方案与计划，从而提升企业经济效益的方法。企业经营管理中的部分问题可以通过线性规划的属性模型表示，利用计算机对模型进行计算，从而得出最优化的解答，使得企业的资源分配更加合理、经营计划更加科学，进而提升企业经济效益。

线性规划与企业经营管理之间有着密切关系。在企业日常管理中往往希望实现最优的经济目标，但由于内部因素与外部环境的限制，在实现目标的过程中往往会受到不同类型的阻碍。因此，目标的实现与目标的阻碍是存在矛盾关系的，但客观上目标的实现及其阻碍之间存在一定的依赖关系，两者既统一，又同处于相同事物中[3]。线性规划就是在这一目标的实现与阻碍的关系中，寻找两者的联系与相互制约的关系，从而建立起来的数学模型[4]。企业管理中经营目标往往包括最大销售利润、最低成本投入、最短运输线路等，而阻碍目标实现的往往是有限的成本投入、人力资源的限制、市场需求量的约束、硬件设备的不足等。线性规划就是在不同客观条件的约束下，高效合理地安排企业的经营活动，实现最优经济目标。线性规划数学模型需要具备以下3个要素：一是一个由若干变量构成的线性目标函数，该目标函数需要取最大值或最小值;二是所有决策变量必须为正数或零;三是决策变量需要满足若干个通常为不等式的线性约束条件。上述3个关键要素直接决定着线性规划模型的数据结构。线性规划的通用数学模型可以缩写如下：

4 数学线性规划在企业管理中的应用

4.1 數学线性规划在企业人力资源管理中的应用

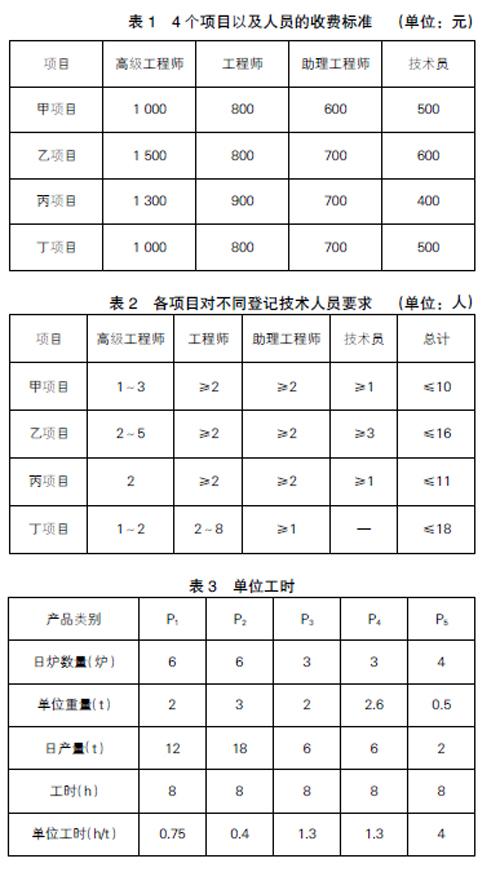
数学线性规划可以用于企业生产组织计划的优化，合理安排企业人力资源，使得经济效益最大化。A企业为建筑企业，现拥有41名技术人员，当前同时承接了4个工程项目，其中2个为建筑工程施工项目，另外2个项目为建筑设计。由于这4个项目均源自不同客户，对项目的完成标准与要求也有所不同，因此A企业对内部人员分配进行了优化处理，也对薪酬做出调整。公司的41名技术人员登记与薪资如下：技术员（5名）每日110元，助理工程师（10名）每日170元，工程师（17名）每日170元，高级工程师（9名）每日250元。表1为4个项目及人员的收费标准;表2为4个项目对不同等级技术人员的数量要求。

由于丙项目、丁项目要在办公室内完成设计工作，所以需要每人每天增加50元的管理费用。根据上述条件与情况，A公司面临的问题是如何合理分配企业现有人员，最大限度地节约成本，获取最高收益。

模型建立过程：制定4类技术人员向甲项目、乙项目、丙项目、丁项目的分配方案。决策变量：在工程项目j中分配第i种技术人员共xij≥0。第i种技术人员的收费标准分别为cij，其中i=1，2，3，4;j=1，2，3，4。目标函数：对不同类别的技术人员分配不同项目所获得的费用，以及公司对不同类别技术人员所花费的支出及管理费用之间的差值进行计算，计算差值最大化，且设立目标函数。约束条件：约束条件可从表1、表2得出。经过计算机软件分析后，得出甲项目分别为高级工程师1人、工程师6人、助理工程师2人、技术员1人;乙项目分别为高级工程师5人、工程师3人、助理工程师5人、技术员3人;丙项目分别为高级工程师2人、工程师6人、助理工程师2人、技术员1人;丁项目分别为高级工程师1人、工程师2人、助理工程师1人、技术员0人。可以得出A公司每天的直接受益最多为27 150元。

线性规划应用在企业人力资源管理中可以兼顾市场需求及企业人力资源现状，在有限的人力、成本环境下实现人力资源的最大化利用[5]。利用计算机计算软件将繁杂的人员配置计划计算得出，让企业能够在激烈的市场竞争中快速制订科学合理的人力资源方案，有效提升企业的工作效率与经济效益。

4.2 数学线性规划在企业生产计划中的应用

生产计划的主要目标在于实现企业利润最大化，生产计划的制订是为生产活动服务的。因此，利用线性规划所建设的生产计划模型可以将成本最小化及利益最大化作为目标函数。企业在安排生产计划的过程中需要考虑不同方面的约束条件，例如企业生产能力的限制、市场需求的限制、生产成本的限制等[6]。在众多限制条件中需要优先考虑生产能力与工时的限制，再搭配生产成本、利润等限制，在这一基础上对企业生产计划进行协调。企业生产产品的成本为C，主要由原料成本（C1）、能源成本（C2）、制造成本（C3）、人工成本（C4）等构成。在归集产品生产成本后，形成生产计划优化模型的约束条件。在成本归集时发现，原料成本与产品单价成正比;能源成本与产品预定分配率成正比;制造成本与产品预定分配率成正比;人工成本与人力薪酬率成正比。在整体产品成本结构中，能源成本、制造成本及人工成本较为稳定，且占比较低。原料成本占据总成本的80%以上，且市场价格波动明显，因此将原料成本考虑为约束条件对生存计划模型的影响。

B为铁合金企业，要在众多约束条件下实现月度生产利润最大化。当前，B企业每月生产量最大为400 t;按照正常生产工作制度，每月有效工时需要控制在176 h内;每月用于生产的原料采购成本需要控制在3 500万元以内。B企业需要生产5个类别的产品，不同品种的单位利润与成本不同。产品1（P1）的单位利润为9万元/吨，所需成本25万元/吨;产品2（P2）的单位利润为3万元/吨，所需成本20万元/吨;产品3（P3）的单位利润为1万元/吨，所需成本1.4万元/吨;产品4（P4）的单位利润为1万元/吨，所需成本1万元/吨;产品5（P5）的单位利润为0.5万元/吨，所需成本1.1万元/吨。B企业的生产时间以工作日单班制为准，平均每日生产8 h。各类产品每8小时所能生产的炉数及其重量见表3。

在这一情况下建立线性规划模型：Smax=cixi;xi≤400;tixi≤176;uixi≤3 500;xi≥0 i=1，...，n。

其中，S为总利润;xi为第i种产品数量;n为产品类别数量;ci是第i种产品的单位利润;ti为第i种产品花费的单位工时;ui为第i种产品投入的单位原料成本。

建立线性规划模型后利用单纯形法获得最优解：B企业P1生产137.7 t，P4生产55.9 t，就可以获得最大利润为1 295.78万元。通过建立线性规模为B企业制订生产计划提供了可靠的依据，在企业有限的资源限制下，制订合理的生产计划，能够让企业最大限度地获取利润。在实际运用中，需要充分考虑不同时期原料单价与销售价格的变化及市场需求的动态发展，根据不同方面的情况修正模型数据，并根据每月的实际情况制订生产计划，实现企业经济效益最大化。

5 结语

企业管理的科学化直接关系着企业战略目标的实现。在市场竞争日益激烈的环境下，企业管理者需要立足于当前，转变以往粗放型的发展战略，发挥企业资源的最大效益。数学线性规划就是一种帮助企业挖掘资源优势，在有限的资源下实现利益最大化的重要工具，为企业管理者调整管理方案、优化生产计划提供了可靠的依据。

参 考 文 献

[1]孟香惠，施保昌，胡新生.线性规划单纯形法的动态灵敏度分析及其应用[J].应用数学，2018，31（3）：697-703.

[2]孙伟東，刘垒垒.线性规划在轨道交通工程经营管理活动中的应用[J].工程技术研究，2018，29（13）：104-105.

[3]张晓澎.线性规划在企业管理中的应用[J].科技经济导刊，2018，26（30）：200-201.

[4]帖新锋.基于线性规划的企业生产计划编制问题[J].消费导刊，2018（48）：114.

[5]刘自新.直觉模糊线性规划在企业生产管理中的应用[J].大连大学学报，2015（3）：1-6.

[6]周冬娥.基于Excel的线性规划在物流企业管理中的应用[J].新余学院学报，2012，17（4）：139-141.