钢箱梁第二体系应力计算分析
2020-12-29任秋云
任秋云
摘 要:在车辆荷载作用下,钢箱梁正交异性钢桥面板受力复杂。本文以某公路钢箱梁桥为例,采用midas FEA实体仿真有限元软件对比不同约束、不同加载位置的情况下钢桥面板第二体系应力大小,从而得出第二体系计算时最不利的约束方式和加载方式,为类似设计、计算提供参考。
关键词:正交异性钢桥面板;第二体系;有限元;应力
中图分类号:U448.27文献标识码:A文章编号:1003-5168(2020)32-0106-03
Abstract: Under the action of vehicle load, the steel box girder orthotropic steel bridge deck bears complex forces. This paper took a highway steel box girder bridge as an example, used midas FEA entity simulation finite element software to compare the stress of the second system of steel bridge deck under different constraints and different loading positions, so as to obtain the most unfavorable constraint method and loading method in the calculation of the second system and provide reference for similar design and calculation.
Keywords: orthotropic steel bridge deck;second system;finite element;stress
鋼箱梁桥具有自重轻、跨越能力强,抗弯抗扭刚度大,钢材拉压性能一致,工厂制造、现场安装、施工工期短,适应性强、适用范围广等优点,在工程中被国内外广泛使用。钢箱梁计算分析通常有两种途径。一是通过有限元分析,建立全桥模型。这种计算分析方式需要建立全桥有限元模型,一次得到整个结构的全部内力,结果详细、全面,但计算所需资料庞大,建模过程复杂,分析耗时过长,对设计者的建模能力及计算机硬件要求较高,一般设计中不建议采用。二是将钢箱梁按三个体系分别进行计算后综合考虑。由于钢箱梁结构各部件之间传力明确,所以采用这种方式计算较为经济、快捷。
第一体系为主梁体系,第二体系为桥面结构体系,第三体系为面板体系。实际应用中,第二体系比较接近实际的受力状态,它的应力按正交异性板理论来计算。但是,第二体系应力分析目前还没有明确的方式,特别是边界条件的处理、车辆荷载的加载位置等。因此,笔者以某钢箱梁为例,采用有限元分析软件建立钢箱梁局部模型,进行第二体系受力分析并得出结论,为类似设计计算提供参考。
1 工程概况
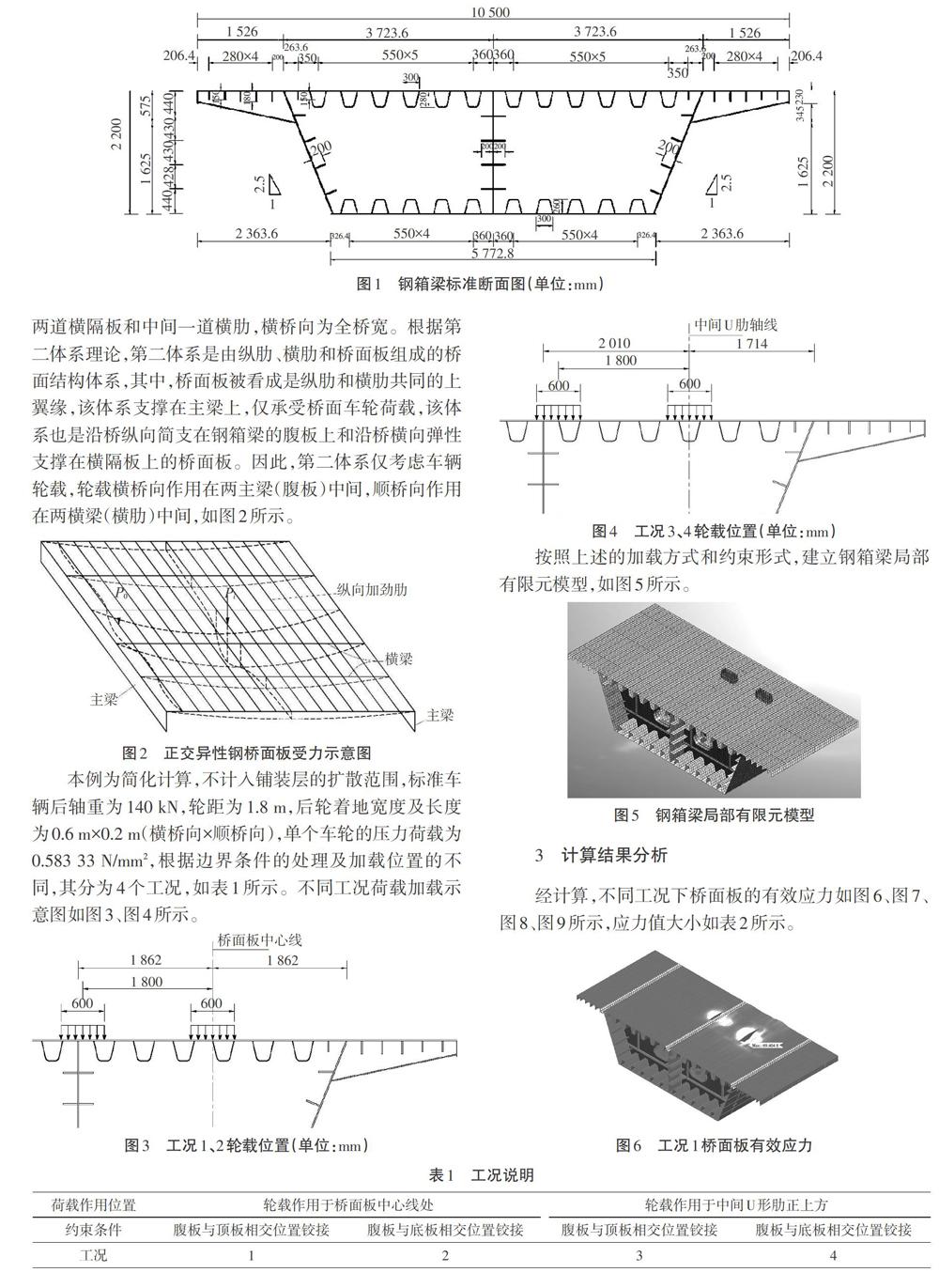
某匝道钢箱梁桥跨径布置为31 m+50 m+39.786 m,桥梁平面位于曲线段,桥宽为10.5 m,钢箱梁采用单箱双室断面,梁高为2.2 m,顶板、底板、腹板厚度均为16 mm,顶底板在支点附近加厚至28 mm,箱室内顶底板采用U形加劲肋,厚度为8 mm,间距为550 mm,悬臂范围顶板及腹板采用板肋,跨中横隔板厚为14 mm,支点横隔板厚为28 mm,横隔板、横肋顺桥向间距为3 m,两者交错布置。该桥设计荷载为公路-Ⅰ级,其采用单向两车道。钢箱梁标准断面图如图1所示。
2 模型建立
第一体系计算采用单梁模型,恒载包括钢箱梁自重、支点处混凝土压重、二期铺装护栏、基础变位作用等,活载包含车道荷载、整体升降温、温度梯度作用。经计算,钢箱梁顶缘最大应力出现在中跨跨中,应力大小为123.2 MPa。
第二体系计算采用有限元分析软件建立钢箱梁局部实体模型,本次建模截取顺桥向4.5 m长度的梁段,包含两道横隔板和中间一道横肋,横桥向为全桥宽。根据第二体系理论,第二体系是由纵肋、横肋和桥面板组成的桥面结构体系,其中,桥面板被看成是纵肋和横肋共同的上翼缘,该体系支撑在主梁上,仅承受桥面车轮荷载,该体系也是沿桥纵向简支在钢箱梁的腹板上和沿桥横向弹性支撑在横隔板上的桥面板。因此,第二体系仅考虑车辆轮载,轮载横桥向作用在两主梁(腹板)中间,顺桥向作用在两横梁(横肋)中间,如图2所示。
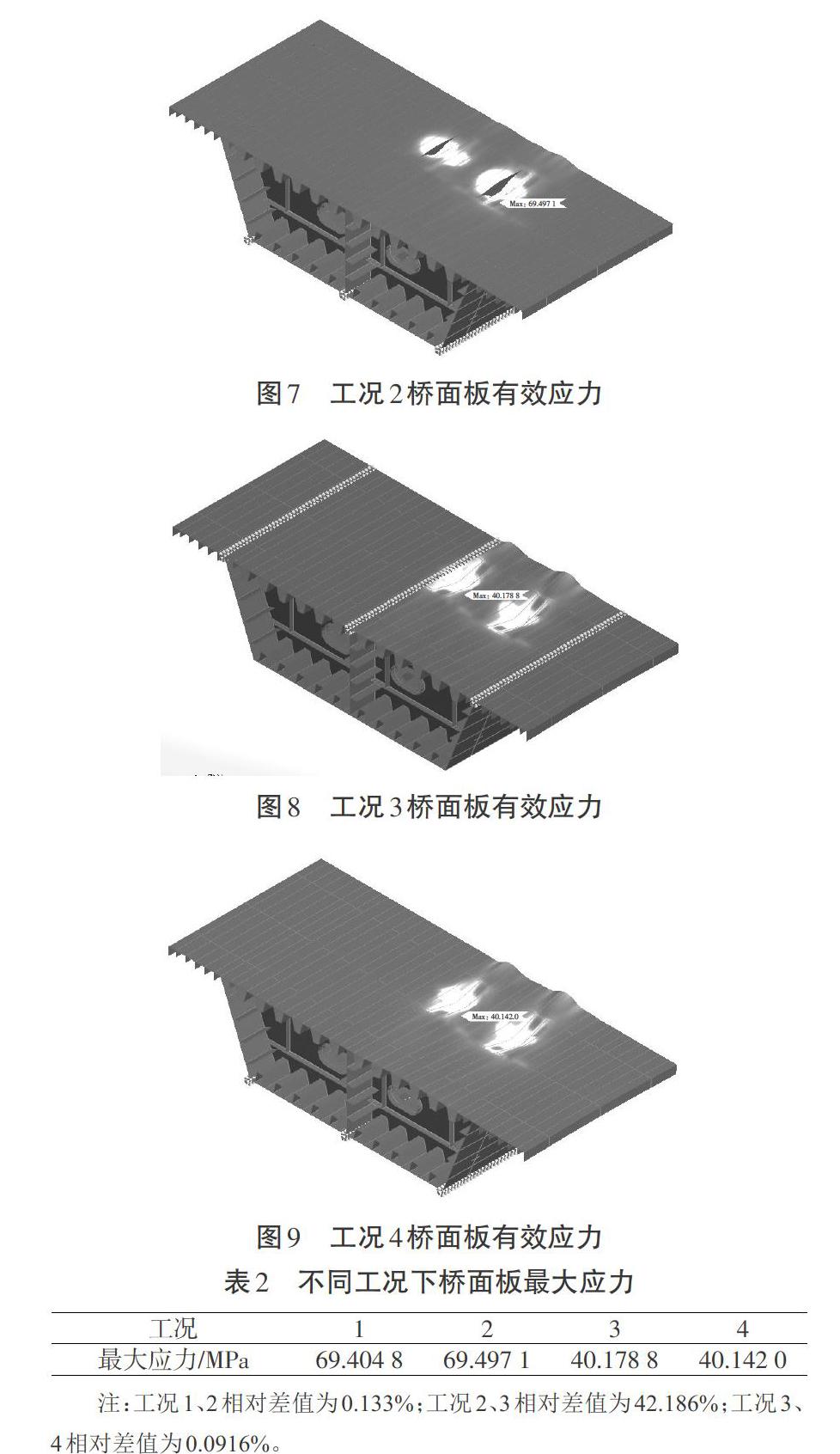
从图6至图9和表2可以看出,当车辆荷载作用在桥面板正中间时,第二体系顶板应力最大,荷载横桥向偏离中心位置约15 cm,应力减少了42.186%,约为25 MPa,最大应力值为69.5 MPa,该结果未计入0.4的冲击系数。综合第一体系、第二体系的计算结果,计入冲击系数0.4,钢箱梁顶板应力=第一体系应力+1.4×第二体系应力=123.2+1.4×69.497 1=220.5 MPa<275 MPa,本例中顶板满足强度理论要求。
4 结论
通过有限元实体仿真分析可知,第二体系计算车辆荷载,仅对车轮周围小范围桥面板影响较大,顺桥向距离车轮边缘20 cm范围以外应力接近0,在车轮位置达到最大值。通过相同荷载条件、不同边界条件的比较可知,约束加在腹板底部或者腹板顶部对结果的影响很小,可忽略不计,计算时只需要严格按照第二体系理论,把桥面板看作是顺桥向简支在钢箱梁的腹板上和横桥向弹性支撑在横隔板上的薄板即可。通过相同边界条件、不同的荷载加载位置的比较可知,汽车轮载横桥向作用的位置对第二体系计算的影响较大,其在桥面板中心位置达到最大值。
第一体系理论浅显易懂,计算方式均有成熟的理论知识和大量的实践经验作为参考,第二体系理论清晰,传力方式明确,但计算方式尚不成熟,很多工程师均处于摸索探求阶段。通过对实际案例进行验算分析,笔者对第二体系应力分布及应力大小影响因素有一定的了解,在此基础上提出一些可以减小第二体系应力的方法,比如适当减小腹板、横隔板间距,适当增加铺装层厚度从而增大车轮在钢桥面板上的受力面积等,使钢箱梁的设计更合理、更安全。
参考文献:
[1]吴冲.现代钢桥[M].北京:人民交通出版社,2006:67-68.
[2]贾高炯.钢箱梁桥设计[M].北京:人民交通出版社,2016:57-58..
[3]交通运输部.公路桥涵设计通用规范:JTG D60—2015[S].北京:人民交通出版社,2015.
[4]樊启武.正交异性桥面系第二体系应力计算方法研究[D].成都:西南交通大学,2005:22-23.
