水压力作用下钢护筒受力性能研究
2020-12-29于文杰窦国涛谢晓鹏高波杨露
于文杰窦国涛 谢晓鹏 高波 杨露

摘 要:针对超深钢护筒在水压力作用下的受力性能问题,本文采用ANSYS进行了不同壁厚钢护筒的有限元模拟。研究结果表明,钢护筒的水平位移和应力随着钢护筒深度的增加而增大;随着壁厚的变大,钢护筒水平位移逐渐减小,壁厚2.5 cm时钢护筒最大水平位移为壁厚0.5 cm时钢护筒最大水平位移的0.172;随着壁厚的变大,钢护筒米塞斯应力极值逐渐减小。壁厚2.5 cm时钢护筒米塞斯应力极值为壁厚0.5 cm时钢护筒米塞斯应力极值的0.164。
关键词:钢护筒;水压力;位移;应力
中图分类号:U445.6文献标识码:A文章编号:1003-5168(2020)32-0005-05
Abstract: Aiming at the mechanical performance of ultra-deep steel casing under water pressure, this paper used ANSYS to carry out finite element simulations of steel casings with different wall thicknesses. The research results show that the horizontal displacement and stress of the steel casing increase with the increase of the depth of the steel casing; As the wall thickness increases, the horizontal displacement of the steel casing gradually decreases, when the wall thickness is 2.5 cm, the maximum horizontal displacement of the steel casing is 0.172 of the maximum horizontal displacement of the steel casing when the wall thickness is 0.5 cm; as the wall thickness increases, the Mises stress extreme value of the steel casing gradually decreases. When the wall thickness is 2.5 cm, the extreme value of Mises stress of the steel casing is 0.164 of the extreme value of Mises stress of the steel casing when the wall thickness is 0.5 cm.
Keywords: steel casing;water pressure;displacement;stress
熊俊華[1]针对高压输水管道钢管外包混凝土结构的力学特性,提出了一种新型无粘结钢管外包混凝土组合结构型式,并结合南水水库供水工程实例,阐述该组合结构在内水压力、土压力作用下的力学模型、工作机理和优势。邓育林等[2]以三种墩高的圆截面深水墩为对象,借助有限元软件建立墩-水相互作用的数值模型,考虑桥墩局部和整体损伤,同时考虑桥梁上部结构的影响,分析不同损伤程度及不同墩顶质量情况下的动水附加质量随水位的变化,并通过动水压力和动力特性分析进行验证。卢华喜等[3]基于势流体理论建立考虑墩-水相互作用的深水圆端型空心桥墩三维有限元模型,分析桥墩考虑内域水、外域水及同时计入内、外域水时不同水位下的动水效应对桥墩自振频率及动力响应的影响,并讨论桥墩壁厚不同时内域水、外域水及同时考虑内、外域水作用对桥墩地震响应的影响规律。陈鹰[4]为研究桥梁深水基础钢管桩围堰结构的受力特性,采用ANSYS Workbench建立有限元模型,对钢管桩围堰结构进行变形及应力分析,考虑在静水压力及动水压力作用下各工况中围堰结构的变形特点及各构件的应力分布情况,得出最不利工况,为现场施工提供技术指导。高海东等[5]以港珠澳大桥拱北隧道曲线顶管管幕工程为背景,针对钢顶管管节密封性能进行了室内模型试验和ABAQUS有限元模拟。
本文针对超高钢护筒在水压力作用下的应力和变形进行了有限元分析。
1 工程背景
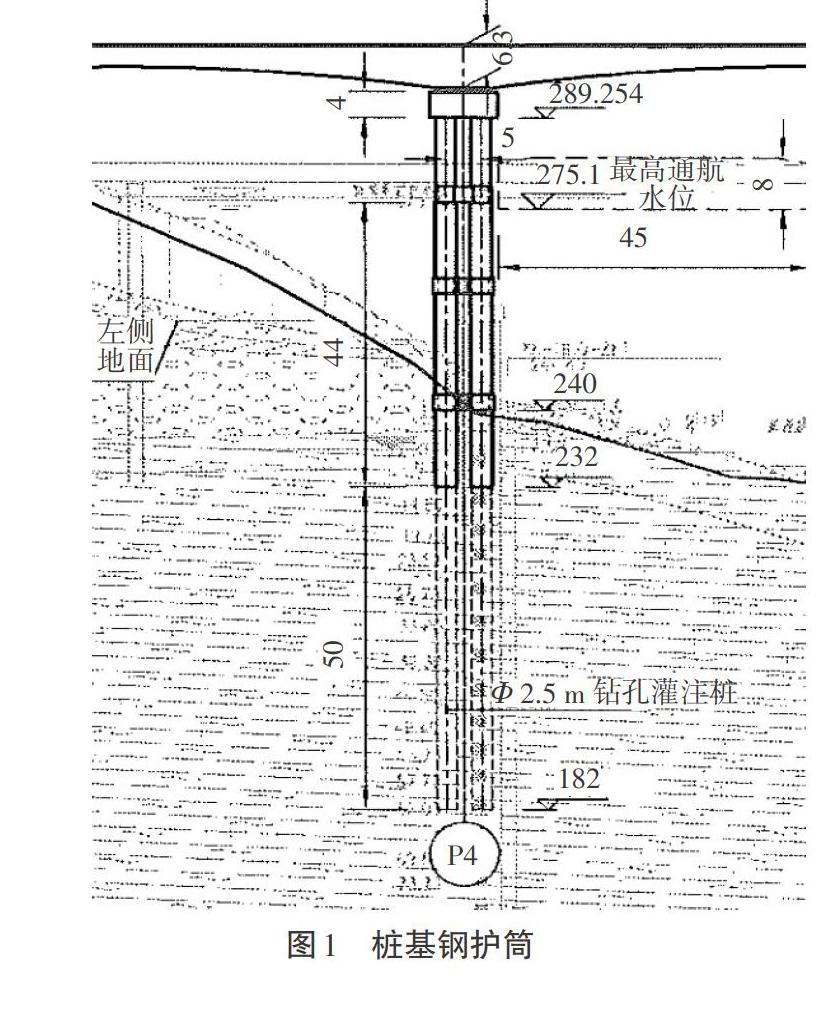
南村黄河特大桥是渑(池)垣(曲)高速公路的控制性节点工程,大桥呈南北走向,全长约为1 727.6 m,总宽为33 m,单幅桥宽为16.25 m,幅间净距为0.5 m。由于本工程处于小浪底库区,水位深、变化大,为减少深水施工的投入与风险,P3-P16主墩设计采用超大直径桩基础,同时采用桩柱一体式的下部结构,主墩承台下设置4根(2×2布置)直径2.5 m的桩基础,横桥向桩间距为6.25 m,顺桥向间距为5.0 m。为方便下部结构施工,P4-P16主墩所有高程+276 m以上部分墩身采用模板施工,直径为2.8 m,混凝土标号为C40,+276 m以下至桩顶部分墩身采用钢护筒施工,钢护筒为永久性结构,设计护筒进入冲止标高以下,具体进入长度可根据实际地质情况确定,此段墩身混凝土采用C40水下混凝土。经设计,墩身钢护筒采用Q345C钢材制作,内径为3.0 m,壁厚为25 mm,其技术指标符合《低合金高强度结构钢》(GB/T 1591—2018)。钢护筒示意图如图1所示。图中,数据单位均为米(m)。
由于本项目中钢护筒高度较大,钢护筒底部插入土中后,尚剩余较大的高度位于水中,本文以P4桥墩为例,对水压力作用下的钢护筒进行受力分析。
由图1可知,钢护筒底部标高232~240 m的部位插入土中,有限元模拟时,底部8 m施加边界条件为全约束,分析水压力作用时,按照极限工况进行分析,钢护筒外部有水,按最高水位275.1 m计算,标高240.0~275.1 m处位于水中,有限元模拟时,水的作用以面荷载形式进行加载,如图2所示。其间可以采用式(1)进行计算。
2.2 工况设置
本文共设置五种工况,工况一为钢护筒壁厚0.5 cm;工况二为钢护筒壁厚1.0 cm;工况三为钢护筒壁厚1.5 cm;工况四为钢护筒壁厚2.0 cm;工况五为钢护筒壁厚2.5 cm。
3 结果分析
3.1 水平位移分析
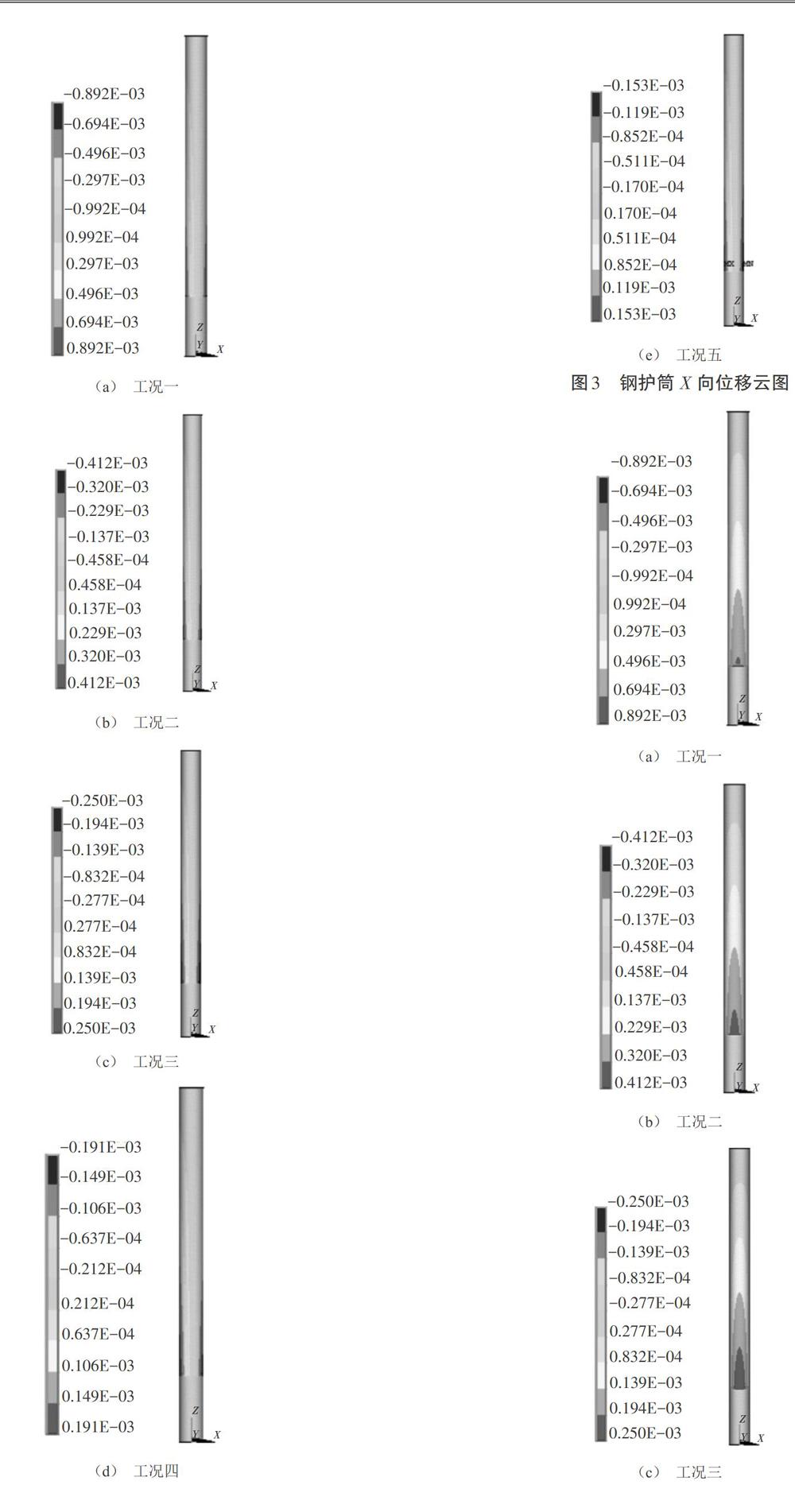
钢护筒在水压力作用下的水平位移云图如图3和图4所示,由于钢护筒是圆形,水压力在同一深度处相同,因此,在同一深度处,两个方向位移一致。图3(a)和图4(a)显示,壁厚为0.5 cm时,钢护筒最大水平位移为0.892×10-3 m;图3(b)和图4(b)显示,壁厚为1.0 cm时,钢护筒最大水平位移为0.412×10-3 m;图3(c)和图4(c)显示,壁厚为1.5 cm时,钢护筒最大水平位移为0.250×10-3 m;图3(d)和图4(d)显示,壁厚为2.0 cm时,钢护筒最大水平位移为0.191×10-3 m;图3(e)和图4(e)显示,壁厚为2.5 cm时,钢护筒最大水平位移为0.153×10-3 m。分析可知,随着壁厚的增厚,钢护筒水平位移逐渐减小,壁厚2.5 cm时钢护筒最大水平位移为壁厚0.5 cm时钢护筒最大水平位移的0.172。
3.2 应力分析
材料(钢材)处于复杂应力状况时,为了判定材料是否进入塑性阶段,人们通常采用米塞斯应力指标。米塞斯应力(Mises应力)是一种折算应力,折算依据为能量强度理论,即第四强度理论[6]。在三向应力(立体应力)作用下,米塞斯应力可按式(2)计算。
式中,[σm]是米塞斯应力,MPa;[σ1]是第一主应力,MPa;[σ2]是第二主应力,MPa;[σ3]是第三主应力,MPa。
水压力作用下的钢护筒应力云图如图5所示。图5(a)显示,壁厚为0.5 cm时,钢护筒最大水平位移为129 MPa;图5(b)显示,壁厚为1.0 cm时,钢护筒最大水平位移为61.9 MPa;图5(c)显示,壁厚为1.5 cm时,钢护筒最大水平位移为38.6 MPa;图5(d)显示,壁厚为2.0 cm時,钢护筒最大水平位移为26.6 MPa;图5(e)显示,壁厚为2.5 cm时,钢护筒最大水平位移为21.2 MPa。分析可知,随着壁厚的增厚,钢护筒米塞斯应力极值逐渐减小。壁厚2.5 cm时钢护筒米塞斯应力极值为壁厚0.5 cm时钢护筒米塞斯应力极值的0.164。
4 结论
本文研究了水压力作用下超深钢护筒的变形及受力,得到如下结论。钢护筒的水平位移和应力随着钢护筒深度的增加而增大;随着壁厚的变大,钢护筒水平位移逐渐减小,壁厚2.5 cm时钢护筒最大水平位移为壁厚0.5 cm时钢护筒最大水平位移的0.172;随着壁厚的变大,钢护筒米塞斯应力极值逐渐减小。壁厚2.5 cm时钢护筒米塞斯应力极值为壁厚0.5 cm时钢护筒米塞斯应力极值的0.164。
参考文献:
[1]熊俊华.新型无粘结钢管外包混凝土组合结构在高压输水工程中的应用[J].吉林水利,2019(5):33-36.
[2]邓育林,汤轲,谭金华,等.考虑结构损伤的深水桥墩动水效应等效附加质量研究[J].武汉理工大学学报(交通科学与工程版),2019(4):605-610.
[3]卢华喜,周珍伟,郑孝辉.基于流体单元法的深水圆端型空心桥墩地震响应分析[J].建筑技术,2017(4):353-356.
[4]陈鹰.桥梁深水基础钢管桩围堰受力特性分析[J].铁道建筑,2018(9):27-30.
[5]高海东,赵涛,马胜利,等.高水压条件下钢顶管管节密封性试验及数值模拟研究[J].现代隧道技术,2015(2):148-154.
[6]鞠彦忠,彭雅轩,田玉梅,等.材料力学[M].武汉:华中科技大学出版社,2013:102-103.
