基于MWOA算法的侧铣加工刀位优化方法

孔森 张立强 冯倩倩

摘  要： 针对圆柱刀侧铣加工非可展直纹面的原理性误差问题，提出了一种改进鲸鱼刀位优化算法，旨在减少侧铣加工时的原理性误差。首先构建单刀位和多刀位下的误差度量函数;其次在鲸鱼算法中引入混沌扰动来更新迭代过程中鲸鱼群体中较差的个体;最后通过MATLAB仿真检验本文算法的有效性。仿真结果表明，该方法相比PSO算法在加工误差上减少了15.7%。

关键词： 侧铣; 非可展直纹面; 改进鲸鱼算法; MATLAB仿真

中图分类号：TP391          文献标识码：A     文章编号：1006-8228（2020）12-01-05

Abstract： Aiming at the problem of fundamental error of non-expansible straight grain surface in cylindrical flank milling， a method based on Modified Whale Optimization Algorithm is proposed to reduce the original error of flank milling. The error functions under single tool location and multiple tool location are introduced， and chaotic disturbance is introduced into the whale algorithm to update the poor individuals in the whale population during iteration. The validity of the algorithm is tested by MATLAB simulation. Simulation results show that this method can reduce machining error by 15.7% compared with PSO algorithm.

Key words： flank milling; non-expansible straight face; Modified Whale Optimization Algorithm; MATLAB simulation

0 引言

高端裝备的零件如航空发动机叶片、机身蒙皮等通常是用一些网格曲面来构建，没有精确的计算公式。直纹面是工程实践中常见且重要的一种曲面类型，其可以分为可展直纹面与非可展直纹面，其中可展直纹面加工比较简单，并不是研究的重点。非可展直纹面由于其法向量沿着直母线方向是变化的，因此在侧铣过程中使用圆柱刀或者圆锥刀都不可避免地存在加工误差。

为了达到更小的加工误差和得到更高精度的零件，诸多学者针对非可展直纹面的原理性误差[1]通过不同的角度和方法进行了探索。LIU[2]将曲面基线上的一对离散点进行偏置得到一组刀轴，这种方法虽然简单，但误差很大;CHIOU[3]将刀具包络面与待加工表面之间的法向距离作为优化函数，通过调整刀具位姿使误差减小;REDONNET等[4]通过复杂的算法使三点相切于工件表面以达到减小误差的目的;严涛等[5]通过4点偏置法和最小二乘法进一步对问题进行优化;SANJEEV等[6]提出了刀具包络面与曲面的两条母线相切的方法，其忽略了直纹面中间误差的优化，使直纹面内部的误差过大;CORNELIA等[7]建立了三步优化算法，三步优化后的误差较大阎长罡等[8]结合圆锥面自身的几何特性，提出了法向映射曲线的概念，将刀具包络面向设计曲面的逼近问题转化为每个刀位下法向映射曲线与特征线的最小二乘逼近问题;HSIEH等[9]将刀轴端点视为寻优粒子，首次把PSO算法引入非可展直纹面的原理性问题的优化过程中;刘红军等[10]利用人工鱼群算法全局收敛性快的特性，首先找到了求解的局部范围，然后利用粒子群算法局部收敛快的特性，找到了局部最优值。在制造业中，尤其在非可展直纹面类零件的生产过程中，其原理性误差问题还没有一种具体的解决方法。本文通过对鲸鱼优化算法[11]（WOA）进一步改进以减少直纹面的原理性误差。

1 误差度量函数的构造

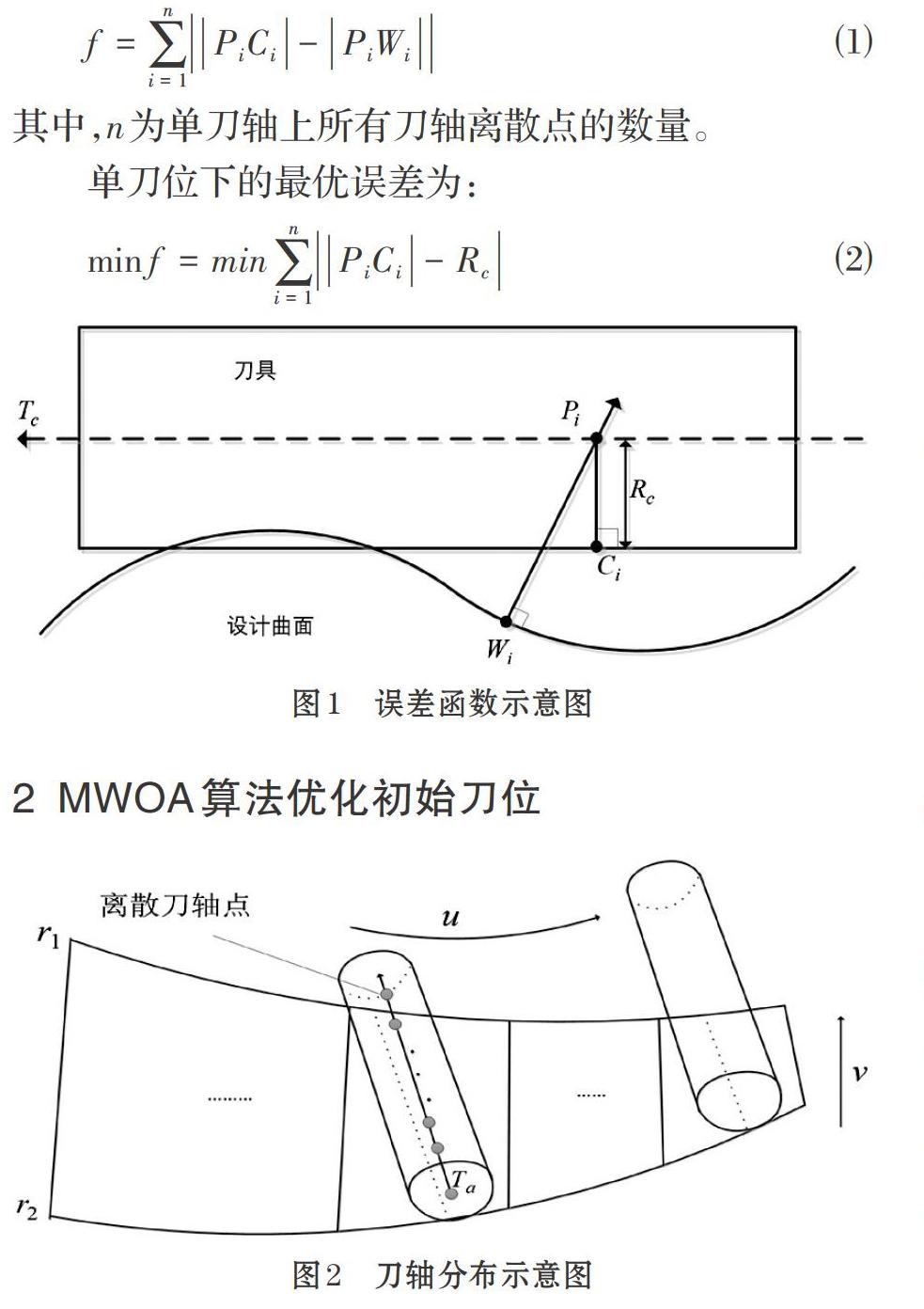
如图1所示，[Tc]为刀轴矢量，[Pi]为刀轴矢量上的某一刀轴离散点，[Ci]为刀具包络面上的一点，其可以理解为点[Pi]在刀具包络面上的映射，对于圆柱刀具而言，[Ci]和[Pi]之间的距离等于圆柱刀的半径[Rc]，[Wi]设计曲面上一点，其可以理解为[Pi]在设计曲面上的映射，[Wi]与[Ci]之间的距离计算可以理解为点到曲面的距离计算。则单刀位下的误差度量函数为：

在构造了误差度量函数后，通过两点偏置法确定初始刀位，随后构建MWOA刀位优化算法调整若干个刀轴以进一步减小误差。经验可知，刀轴数目越大，刀轴形成的轨迹面越精确，但计算效率却会下降。刀轴矢量的分布如图2所示，26个刀轴被作为初始优化目标，把刀轴离散为11个数据点，通过MWOA刀位优化算法，计算这11个离散数据点下最小加工误差，能够求得单刀位下最优刀轴矢量。

2.1 混沌优化WOA的思想

混沌算法是一种简单但具有重要意义的算法[12]。文章为了提高鲸鱼种群的优越性，对该鲸鱼种群中适应度差的鲸鱼进行混沌更新，可以提高WOA刀位优化算法整体优化精度。MWOA的构建思想是把混沌策略引入鲸鱼算法优化刀轴矢量的方法中，其通过小波变换把混沌的运动范围载波进入刀轴的优化变量范围，给刀位群体中最差的刀位引入一个混沌扰动，通过不断更新鲸鱼的位置得到最优刀轴矢量。本文选则logistic映射产生混沌变量：

2.2 MWOA刀位优化算法的构造

MWOA刀位优化算法能够在更新群体中适应度较差个体的同时实现对问题的优化求解。随机在以偏置点为中心的半径等于5毫米的两个球形区域中产生鲸鱼个体[w1（x1，y1，z1）]和[wn（xn，yn，zn）]，组成一组鲸鱼对，构成刀轴矢量[Tα];重复[m]次，得到[m]个六维矢量作[（x1，y1，z1，xn，yn，zn）]为初始种群。

[w1（x1，y1，z1）]和[wn（xn，yn，zn）]是待求的刀轴两端点，其也在刀轴离散点误差的计算之内，由于所在的搜寻区域为半径等于5毫米球型区域，搜索区域较大，可能出现端点越界的情况，造成较大的误差。如图3所示，[w1]为优化过程中刀轴的首端点，[wn]为刀轴的末端点，[Tα]为当前刀轴矢量，设计曲面表示为[s（u，v）]，[P1]为[w1]到曲面上最近的一点，[Pm]为[wn]到曲面上最近的一点，[w2]为第二个刀轴离散点。以首端点[w1]为例，若其所在位置在[u∈[0，1]]之外，则判定为越界，越界会造成较大的计算误差，需要重新对两端点所在的位置进行规划以减小计算误差。

如图3所示，[wwi]为第一个刀轴离散点[w1]和第二个刀轴离散点[w2]之间的一点，[wwi]的位置可以认为是[w1]和[w2]之间的均分点，[i=（0，1，2，…，z）]。无论[w1]越不越界，首先计算[w1]到曲面[s（u，v）]的距离的最近点[P1]，得到[P1]的位置之后，计算每一个均分点[wwi]与[P1]之间的距离[di]，若存在[di

改进鲸鱼刀位优化算法执行过程可按如下步骤。

Step1 MWOA刀位优化算法中参数的设定。需要设定的参数包括迭代最大次数[N]、混沌更新的最大执行次数[F]，变量的界限为[xlowi]和[xtopi]，同时设定初始最优目标函数值为[M]。

Step2 随机初始化刀轴的位置。按照公式[xi=xtopi-xlowirand（）+xlowi]随机生成[n]个初始刀轴刀位。

Step3 确定当前刀位的最优目标值[fbest]与最优刀位。刀轴端点越界处理后，根据误差度量函数定义式⑵计算当前刀位群中各个刀位的目标函数值并与当前最优目标值比较，按照优化目标最小化规则确定出刀位群的最优目标值，其相应刀位即为当代最优刀位。

Step4 当前最差刀位的筛选及其混沌赋值过程。将当代刀位群中目标值最大的刀位作为被更新个体[Bnew]，采用如下的混沌搜索策略对其进行位置更新。

① 利用混沌更新函数式⑶，更新该刀轴两端点的位置，刀轴端点越界处理后，比较新刀位与原刀位[Boriginal]的误差函数值，若新刀位优于原最差刀位则更新位置，反之则个体[Bnew]位置不变。

② 在原最差刀位被更新的前提下，比较新刀位与当前最优刀位的误差函数目标值，当新刀位优于当前最优刀位时更新最优刀位，反之最优刀位不变。

③ 判断混沌更新次数C是否达到最大值，若是，则返回执行Step5，反之C增加1并执行步骤①。

Step5 按文献[11]中WOA算法信息继承方式生成新刀位群并进行解的有效性判断。优化过程中，在两种寻优机制（收缩包围和螺旋泡泡网）之间随机选择一种机制进行搜索，更新刀位并产生新的刀位群，通常随机概率选为0.5。以[xlowi]和[xtopi]为界限判断刀位的有效性，若跃界则在区间内产生新刀位，反之则保持不变。

Step6 判断是否达到最大迭代次数[N]。若是则输出最优函数值和最优刀位的位置;否则返回Step3继续进行迭代计算。

通过上述改进鲸鱼算法可得到所有优化后的刀轴矢量和刀轴端点值。

3 数值算例

设计曲面其造型如图4所示，其2条基线的节点矢量为[0，0，0，0，0.2，0.4，0.6，0.8，1，1，1，1]。

使用半径为5mm的圆柱刀，并将整个设计曲面分成[0，0.04]，[0.04，0.08]，[0.08，0.121]，…，[0.92，0.96]，[0.96，1]25个子区域，用[M=25]表示，即参数u分别等于0，0.04，0.08，0.12，…，0.96，1，选取26个刀位，计算刀轴上均布的11个点的总误差。

根据PSO算法对刀轴优化的先前研究经验，把PSO和MWOA刀位优化算法的种群搜索个体的数目设置为50，最大迭代次数设为100次，本文混沌更新次数设为100次，。对两点偏置法、PSO、MWOA三种不同的刀位优化方法进行分析。图5为u=0.2时两种算法单刀位最优值的收敛情况，当迭代次数达到65次和58次以上时收敛趋于平缓，PSO算法收敛于0.026mm，MWOA算法收敛于0.022mm，MWOA算法在其他刀轴的收敛情况相似。图6表示u=0.2处的最优解，其中，离散的点所在直线为优化后的刀轴矢量，端点内测的点代表刀轴两端点经边界处理后的位置，以图6b为例，未经边界处理前的两端点位置为[102.4317，39.2816，26.5421]、[125.2001，50.3714，51.0000]，越界处理后的两端点位置为[103.3424，39.7252，27.5204]、[124.2893，49.8169，50.0217]。通过误差计算，两点偏置法和两种优化算法的加工误差对比如图7所示，对设计曲面的11×21个网格节点进行误差计算，其中在初始刀具轴迹面下，加工误差平均值为0.054mm;在PSO算法优化后的刀具轴迹面下，加工误差的平均值为0.00242mm，较两点偏置法加工误差减少了95.5%;在MWOA算法优化后的刀具軸迹面下，加工误差平均值为0.00204mm，加工误差较PSO减少了15.7%。图7中负值表示过切现象，正值表示欠切现象。

4 结束语

本文以圆柱刀侧铣加工为例，基于MWOA刀位优化算法对侧铣单位刀轴矢量进行优化。将本文算法与传统两点偏置法进行仿真对比分析发现，基于MWOA刀位优化算法侧铣加工时的刀轴误差得到了明显减小。同时与广泛研究的PSO算法进行进一步的仿真对比分析，数值计算结果为平均误差减少了15.7%，一定程度上提高了零件加工质量，对非可展直纹面的侧铣加工有一定的指导意义。

参考文献（References）：

[1] HSIN T H， CHIH H C. Improving optimization of tool pathplanning in 5-axis flank milling using advanced PSO algorithms[J].Robotics and Computer-Integrated Manufacturing，2013.29：3-11

[2] Liu X W. Five-axis NC cylindrical milling of sculpturedsurfaces[J].Computer-Aided design，1995.27（12）：887-894

[3] CHIOU C J. Accurate tool position for five-axis ruledsurface machining by swept envelope approach[J]. Computer-Aided Design，2004.36（10）：967-974

[4] REDONNET J M，RUBIO W，DESSEIN G. Side milling ofruled surfaces：Optimum  positioning of the milling cutter and calculation of interference[J].International Journal for Advanced Manufacturing Technology，l998.14：459-465

[5] 严涛，刘志兵，王西彬等.基于四点偏置法的非可展直纹面侧铣刀位计算[J].图学学报，2015.6.

[6] SANJEEV B，STEPHEN M，CORNELIA M. Flank millingwith fiat end cutter[J].Computer Aided Design，2003.35：293-300

[7] CORNELIA M， SANJEEV B，STEPHEN M. Triple tangentflank milling of ruled surfaces[J].Computer Aided Design，2004.36：375-378

[8] 閻长罡，刘宇，崔云先等.圆锥刀侧铣非可展直纹面刀轴轨迹规划的特征线方法[J].机械工程学报，2015.51（19）：206-212

[9] HSIEH H T，CHU C H. Optimization of Tool Path planning in 5-axis flank milling of ruled surfaces with improved PSO[J].International Journal of Precision Engineering & Manufacturing，2012.13（1）：77-84

[10] 刘红军，魏宇祥.基于人工鱼群和粒子群优化混合算法的侧铣刀轴轨迹规划[J].中国机械工程，2018.23.

[11] MIRJALILI S，LWIS A. The whale optimization algorithm[J].Advances in Engineering Software，2016.95：51-67

[12] 邓伟，张其万，刘平等.基于双种群遗传混沌优化算法的最优时间轨迹规划[J].计算机集成制造系统，2018.1.