一种求解多目标优化问题的改进蚁群算法

罗艳媚

摘要：针对带约束的多目标优化问题，提出一种改进的蚁群算法（Ant colony optimization，ACO）。在基本算法的基础上，通过对初始信息素进行混沌处理，动态调整参数α（信息启發式因子）和β（期望启发式因子）值，引入最大-最小蚂蚁系统来对算法进行改进，利用Pareto 的排序机制对搜索到的可行解进行分类排序，得出可行解。对4个经典测试函数的仿真结果表明，文中算法在均匀性、寻有能力均优于另两种算法。

关键词：约束问题;多目标优化;蚁群算法;仿真

中图分类号： TP181        文献标识码：A

文章编号：1009-3044（2020）32-0226-04

在当今科研与工程实践中，决策者需要考虑的因素越来越多，处理的问题越来越复杂，往往需要同时处理多个相互关联且矛盾的多目标函数优化问题。ACO作为一种启发式智能优化算法，能够较好地解决这类问题，但在求解离散型问题中也存在易陷入局部最优、搜索时间较长，收敛较慢等不足。对此，已有学者通过对ACO算法本身的结构和参数进行优化，如：文献[1]对算法初始时刻信息素浓度进行改进，在信息素更新规则中引入自适应动态因子，提高算法搜索能力;文献[2]提出动态自适应调整信息素挥发系数并验证其有效性;文献[3]则引入随机变量来调整对伪随机选择和轮盘赌的选择，平衡开发当前搜索路径与探索其他新路径之间的关系。文献[4]利用初始正反馈的机制来更新负反馈信息素矩阵，避免蚂蚁的重复探索。此外，蚁群算法作为一种进化算法，与遗传算法、粒子群算法、模拟退火算法等其他优化算法结合，充分利用智能算法的互补性，进而提高算法的性能。

上述改进ACO算法在不同程度上提高了搜索效率和收敛速度，但在处理多目标问题时，一般采用线性加权法或顺序法将多目标转化为单目标来求解。这种方式比较简单，但不能很好地平衡存在冲突关系的多个优化目标。为此，本文针对带约束的多目标优化问题提出一种改进的ACO算法，混沌初始化信息素，动态调整α和β参数值，并引入最大-最小蚂蚁系统来限制信息素浓度，利用Pareto排序对搜索到的可行解进行评价。最后，对经典测试函数进行仿真实验，实验结果表明所提算法在求解带约束的多目标问题的可行性及有效性。

1 改进的ACO算法

1.1 基本ACO算法

ACO算法是受到自然界中蚂蚁觅食行为的启发而衍生的一种算法，最早适用于解决TSP（旅行商问题）。蚂蚁觅食过程中，碰到还没走过的路口，随机选择一条路走，同时，在其经过的路径上释放与长度成反比的信息素。后来的蚂蚁碰到已经走过的路口时，选择信息素浓度较高路径。蚂蚁个体之间通过信息素来传递信息。在单位时间内，访问蚂蚁越多的路径，其信息素浓度越强，被选择的概率越大，未被访问的路径其信息素浓度会随着时间而挥发。最终，所有的蚂蚁都选择同一条路径为蚁巢和食物之间的最短路径。

ACO算法在求解优化问题时，把食物的位置抽象成为解的空间点，代表问题的潜在解。设有[n]个节点有向图，[m]只蚂蚁，用[dij（i，j = 1，2，...，n ）]表示节点[i]和[j]之间的距离，初始信息素均一样，即[τij0=c]（[c]为常数）。蚂蚁个体在搜索时，从当前节点i选择概率值较大的节点j作为下一个转移点，概率值[Pkij（t）]跟信息浓度及启发信息有关，其计算公式为：

1.2  Logistic混沌映射

混沌是指发生在确定性系统中的不可重复、不可预测的随机不规则扰动现象，具有不确定性，是非线性动力系统的固有特性。其数学表达式为：

式中：[xn]为混沌变量，n为迭代次数，[μ]为控制系统混沌行为的参数，一般取值范围为 [0，4]，当[μ=4]时，系统处于完全混沌状态，产生的值在[0， 1]内。

采用上使产生初始信息素，充分地利用混沌的遍历性，克服了基本ACO由于初始时刻各路径上信息素相等而盲目进行搜索。

1.3参数的动态调整

基本ACO中，α和β值是固定，在本文中，动态调整α和β值，即其值随迭代次数的变化而变化。算法在搜索初期，以路径长度为依据来引导算法的搜索，此时产生[α∈（0，0.5）]、[β∈（0.5，0.9）]之间的随机数;在搜索后期，产生α为（0.5，0.9）、β为（0，0.5）之间的随机数，将算法调整为依靠信息度浓度进行搜索，有利于增强算法的搜索能力。参数α、β和迭代关系如下：

1.4 最大-最小蚂蚁系统

为了避免算法因信息素积累过高而陷入局部最优，在算法中融合最大-最小蚂蚁系统的思想。

① 将各路径上的信息素浓度限值在[[τmin，τmax]]范围之内，当[τ>τmax]，则[τ=τmax]大于最大值的取[τmax]，当[τ<τmin]，则[τ=τmin]。

②在每次迭代后，只更新最优解对应的路径上的信息素浓度;

③本文算法将初始时刻的信息素浓度设置为[τ0]，上限值[τmax]为[1.5τ0]，下限值[τmin]为[0.3τ0]，即：

1.5 改进算法的具体实现步骤

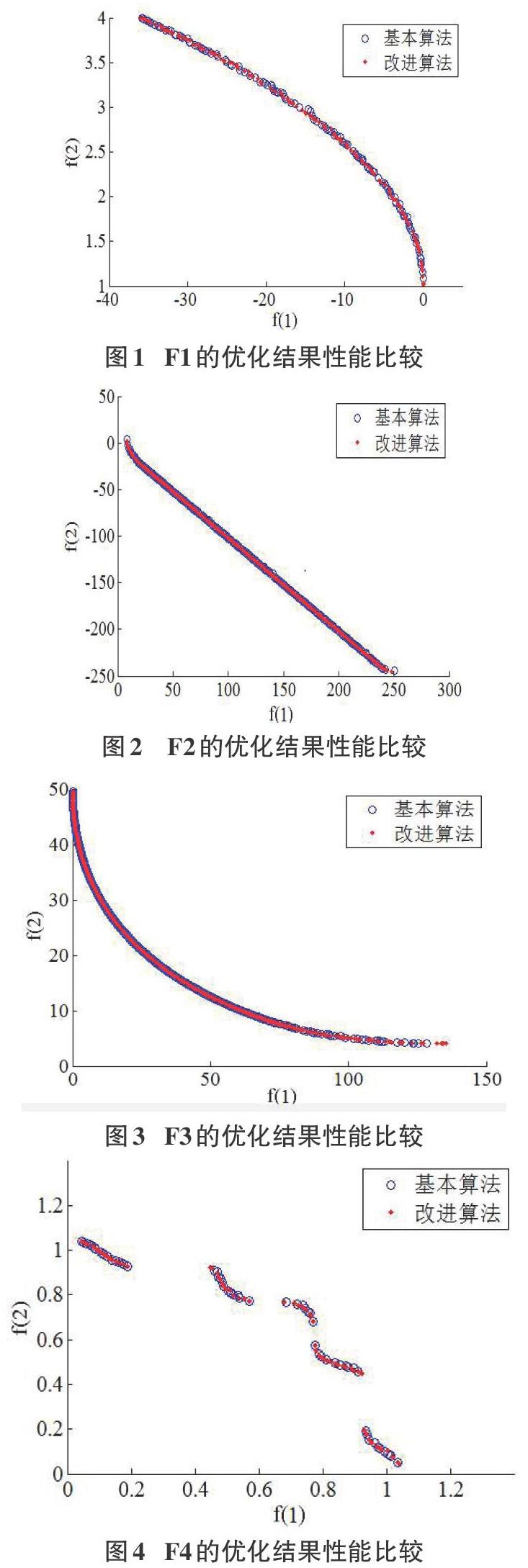
2 算法验证及结果分析

2.1 评价指标与测试函数

2.1.1 评价指标

为了验证算法的性能，本文采用以下三个指标来评价算法的性能。

1）间距评估S

衡量算法结果分布度的指标，S越小，均匀性越好。

2）可行解的个数N

在约束条件内搜索到可行解的个数，N越大说明算法的寻优能力越强。

3）最大散布范围D

两个极值解间的距离，D越大，表明算法的解散布范围越广。