图像去模糊处理研究
2020-12-29付蕊李常芳施淑仙赵加敏
付蕊 李常芳 施淑仙 赵加敏

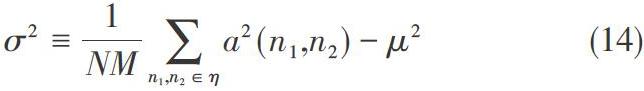
摘要:為减小噪音对图像的影响,结合小波阈值去噪算法和维纳滤波去噪算法两者的优势进行改进,提出一种图像去噪效果更好的方法。该方法首先对图像添加高斯白模糊,模拟图像在不同程度下的模糊情况,其次对添加了不同高斯白噪声下的图像分别进行小波阈值、Wiener滤波、小波阈值和Wiener滤波联合去噪,对比不同不通滤波在相同条件下的去噪效果,最后,计算出降噪之前以及降噪之后的图像信噪比、峰值信噪比。仿真结果表明,该方法的信噪比和峰值信噪比大于比单独使用Wiener滤波和单独使用小波阈值去噪,图像的还原度也较之两者要好。
关键词:小波变换;小波阈值;维纳滤波;图像去噪;图像去模糊
中图分类号:TP311 文献标识码:A
文章编号:1009-3044(2020)32-0189-03
Abstract: In order to reduce the influence of noise on image, combining the advantages of wavelet threshold de-noising algorithm and Wiener filter de-noising algorithm, a better image de-noising method is proposed. First to add white gaussian blur image, this method simulated images under different degree of fuzzy, secondly to add images under different white gaussian noise wavelet threshold, wiener filtering, wavelet denoising threshold and wiener filtering, compare of the filter under the condition of same denoising effect, finally, calculate the noise before and after noise image signal-to-noise ratio, peak signal to noise ratio. Simulation results show that the signal-to-noise ratio (SNR) and peAK-to-noise ratio (PSNR) of this method are greater than those of wiener filtering and wavelet threshold denoising alone, and the image restoration degree is better than both of them.
Key words: wavelet transform; wavelet threshold; wiener filtering; image denoising; image deblurring
1 引言
通过科学研究可知,人类从外界获取的所有信息中有75%以上的信息都是通过视觉系统获得的[1]。随着互联网和通信技术的发展,信号从模拟信号逐渐转变为数字信号,并逐渐成为人类获取、利用、传输信息的主要来源。这是因为数字信号有着以下几个优势:(1)数字信号在信号质量方面的强度以及抗干扰性都要优于模拟信号;(2)数字信号相对于模拟信号更适合远距离的传输以及性能差的线路;(3)数字信号在保密性方面也较之模拟信号更为安全。但数字信号也存在着一些不足:(1)占用频带较宽;(2)处理信息量大;(3)由于外界噪声的干扰很容易导致图像中部分信息的缺失,导致视觉效果变差。这不仅影响了人们对图像的视觉体验,还对后续处理图像的清晰度以及精准度产生了影响。所以,对图像进行去噪是对后续图像处理的重要前提条件之一,减少了噪声对图像的干扰,后续处理工作也会变得简单许多。图像去噪主要有两种方法:空间域去噪和频域去噪。空间去噪算法主要是利用各种图像的平滑模板通过对图像的像素进行变换以达到降低或消除噪声的目的。但是经过滤波后,图像过于平滑,边缘保留能力较差。典型的空间去噪算法有Wiener滤波[2]、均值滤波和中值滤波。频域去噪算法主要是在图像变换后选择合适的带通滤波器进行滤波,得到变换后的去噪图像。由于噪声表现出的高频特性,所以可以将高频信息去除以达到去噪的目的。典型的频域去噪算法包括高通滤波和低通滤波。
本文研究的是图像去模糊处理,需要用到Wiener滤波以及小波变换,因此重点对Wiener滤波以及小波变换的研究现状进行介绍。文献[3]首次提出了小波变换的概念,它可以在时域和频域之间进行局部变换,从而从信号中提取出有效的部分。文献[4]提出了小波软阈值去噪算法和小波硬阈值去噪算法,它不仅提高了小波函数的去噪效果,还提高了图像信噪比以及图像质量。文献[5]提出了小波半软阈值去噪,它与小波软阈值函数和小波硬阈值函数相比,该方法提高了图像信噪比。文献[6]提出了一种改进的阈值去噪的方法,它首先使用小波分析对图像进行分解,分解后得到四个子带系数矩阵,其次使用模糊滤波器确定垂直,水平和对角线方向上的子带系数,最后,通过使用Wiener滤波器对低频区域的子带小波系数进行滤波处理。文献[7]首次提出了Wiener滤波,为图像去模糊提供了新的方法。
自小波变换被发现以来,很大程度上解决了信号与降噪的难题,利用小波降噪有三种方法:基于小波模极大值原理、小波变换系数的相关性以及小波阈值函数法[8]。针对小波变换中的小波阈值的优势,本文选用小波阈值与Wiener滤波相结合的方法进行图像去噪。在降噪的过程中,图像中的目标边缘会因为滤波而变得模糊不清,对图像质量的提高造成了阻碍。因此,图像去模糊技术是图像处理与恢复中的重要处理技术。本文针对图像边缘的模糊和图像去噪算法进行研究,以小波变换以及维纳滤波为基础,对图像去噪算法进行更深的研究。
2 小波变换
实际上,信号的低频部分L和高频部分H是通过低通滤波、高通滤波和二进制下采样得到的。利用一系列一维小波变换可以得到二维小波变换。m行n列图像的二维小波变换过程是将每一行变换成一维小波变换,得到图像的L和H部分。然后对LH图像(仍然是m行n列)进行一维小波变换。这样,第一级小波变换后的图像可以用LL、HL、LH、HH表示,其中LL表示原始图像的低频信息的主要部分,LH、HL、HH分别表示为水平、垂直和对角高频分量。图1为一阶和二阶小波变换的分解图。
式中: h 和g分别表示为尺度函数和小波函数的低通滤波器和高通滤波器;Sf(0,k)为原始信号 f(k);Sf(j,k)为尺度系数;Wf(j,k)为小波系数。
一般而言,小波阈值去噪流程主要分为以下三个步骤,其流程如图2所示。步骤如下所述。
(1)小波变换。根据选择的小波基和分解级m,用m级小波对含噪数据进行分解。
(2)阈值处理。保持图像信号的形状不变,不处理通过分解后的低频小波系数,对每层的高频小波系数wj,k(D)进行阈值化处理,得到?j,k(D)。
(3)小波重构。通过对小波系数?j,k进行阈值处理后,重构以得到目标信号的逼近?(n)。
3 Wiener滤波
经典Wiener滤波不仅是一种从声音中提取有效信号的线性滤波方法,而且其原理还可以使得原始图像和恢复后的图像两者之间的均方误差最小。在信号系统中,假设h(n)為单位样本响应,输入含噪声信号为x(n),输出信号为Y (n),如果输入信号含有噪声,则为:
此时s(n)表示为信号的真实值,v(n)表示为噪声,则输出信号为:
其中:n为连续函数h(n)和x(n)的连续变量;m是积分假变量。滤波结果的目的是使得输出信号y(n)尽可能接近s(n),因此,y(n)被称为s(n)的估计量,用[s(n)]表示,即:
当均值方差[ξ(n)]最小时,滤波去噪效果最好。
图像处理中,Wiener滤波可以根据图像中每个像素估计出的局部均值μ以及方差[σ2],通过下式所述的方法,将噪声方差[ν2]从原始图像中去除,已达到含噪声图像去噪的目的。
4小波变换和Wiener滤波联合去噪
使用Wiener滤波去噪具有以下优缺点。
优点:① 它有着广泛的应用;② 对于某些问题,可以先求出滤波器传递函数的显式解,其次再使用由简单物理单元组成的Wiener滤波器。
缺点:① 在半无限时间间隔内很难获得全部的观测数据;②不能用于非平稳噪声的随机过程;③不便于矢量应用;④去噪时,图像的边缘信息会遭到破坏,是的图像边缘会变得模糊不清。
使用小波阈值去噪具有以下优缺点。
优点:①适应性广泛;②方法简单;③去噪效果好;④去噪后图像细节信息保留较好。
缺点:①经过硬阈值去噪后的图像不能很好地保存图像的细节信息;②经过软阈值去噪后的图像会相较于原始图像会变得模糊[11]。
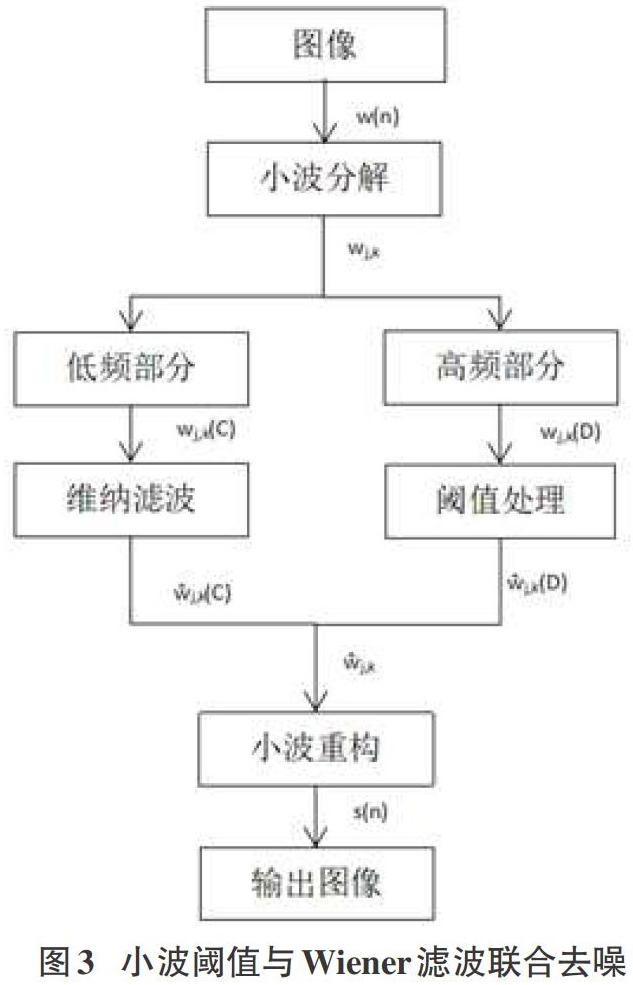
图像去噪重点研究的是噪声的去除以及图像细节的保留[12],本文针对小波变换和Wiener滤波两者各自的优点,通过将两者的优点相结合,对原有算法进行改进,其流程图如图3所示。具体步骤如下所述。
(1)对含有噪声信号的图像进行小波分解,并根据选择的小波基以及分解度m对图像进行小波分解。
(2)提取小波分解中的低频图像并且保留低频小波系数,之后在三个方向上对高频小波系数wj,k(D)进行阈值化处理得到?j,k(D)。
(3)重建新的小波分解结构以获得目标信号?(n)。
(4)对经过小波重构后的图像进行Wiener滤波处理,以获得去噪后的Wiener滤波图像。
5 实验结果与分析
为了验证小波变换与维纳滤波相结合的去噪效果,选取测试图像Lena.bmp作为本文的输入图像,使用的软件为MATLAB 2016a版本。在输入图像中加入方差为0.1、0.05、0.005的高斯白噪声,分别进行Wiener滤波去噪、小波阈值去噪以及小波阈值与Wiener滤波联合去噪,通过MATLAB进行仿真实验。在仿真实验中,Wiener滤波器采用3×3模板,小波去噪采用coif3对图像进行分解。基于小波变换和Wiener滤波,利用小波coif3将图像分解为两个层次。首先用3×3模板的Wiener滤波器对图像进行去噪,其次对经过Wiener滤波处理后的图像进行小波分解,最后,从第一层小波分解中提取低频图像,即实现低通滤波。三种算法的实验结果如图4所示。
为了能更好地展现出这三种算法的去噪效果,本文选用了图像的方差(MSE)、信噪比(SNR)和峰值信噪比(PSNR)这三个评价指标,三种添加了不同程度的高斯白噪声的评价指标如表1、表2、表3所示。
对比三个表不通滤波的方差(MSE)、信噪比(SNR)和峰值信噪比(PSNR),不难发现,高斯白噪声的值越大,方差(SNR)也就越大,而信噪比(SNR)和峰值信噪比(PSNR)越小,去噪后图像的质量也更好。在同一噪音的影响下,小波变换—Wiener滤波的信噪比和峰值信噪比都小于其他两种滤波,噪音的影响越小,小波变换—Wiener滤波与其他两种滤波的峰值信噪比差值越大。
6 结语
本文基于将Wiener滤波器与小波变换融合的优势,明确提出了一类将小波变换与Wiener相结合的算法。该算法结合了小波变换的特点,易于完成和求解。它可以轻松地组合高频和低频信号的特性,并轻松消除每个部分中的噪声成分。Wiener滤波在解决细节上的优势促进了该算法的整体解决了高频和低频的内容以及图像的主要内容。仿真实验成果表明,采用小波阈值和Wiener滤波的联合去噪的方式与单独的小波阈值去噪或单独的维纳滤波去噪相比,可获得更接近初始信号的波形,并且获得的去噪指标信噪比(SNR)和峰值信噪比(PSNR)较大,从而结果表明,本文提出的去噪方法相较于其他两种去噪方法具有较强的去噪效果。
参考文献:
[1] 陈凤珠,陈志刚.图像去噪的研究现状及发展趋势[J].科学与财富,2011(4):240.
[2] 王瑞,張友纯.新阈值函数下的小波阈值去噪[J].计算机工程与应用,2013,49(15):215-218.
[3] Goupillaud P,Grossmann A,Morlet J.Cycle-octave and related transforms in seismic signal analysis[J].Geoexploration,1984,23(1):85-102.
[4] D.L.Donoho.De-noising by soft thresholding[J].IEEE Transactions on Information Theory,1995,41(3): 613-627.
[5] H.Y.Gao,A.G.Bruce.WaveShrink with firm shrinkage[J].Statistica Sinica,1997,7(4);855-874.
[6] 任获荣,张平,王家礼.一种新的小波图像去噪方法[J].红外与激光工程,2003,32(6):643-646.
[7] N.Wiener.Extrapolation,Interpolation,and Smoothing of Stationary Time Series,with Engineering Application.Tech.Press of M.I.T.and John Wiley & Sons,New York,1949.
[8] 卢广森.基于改进阈值函数的小波去噪及其优化研究[D].昆明:昆明理工大学,2017.
[9] 杨兴明,吴永忠,孙锐,等.基于小波多分辨率分析和新的阈值自适应的信号去噪[J].合肥工业大学学报(自然科学版),2007,30(12):1580-1583,1587.
[10] 郭蕾,田松,许悦雷,等.一种小波自适应比例萎缩去噪改进算法[J].电视技术,2012,36(11):27-29,46.
[11] 王民,文义玲.常用图像去噪算法的比较与研究[J].西安建筑科技大学学报(自然科学版),2010,42(6):895-898.
[12] 龙振弘.数字图像去噪典型算法的分析比较[J].福建广播电视大学学报,2009(1):67-69.
【通联编辑:梁书】
