奇异数-1的双重子奇特态

戴连荣, 周亚楠, 扈 岩, 刘诗琪, 蔡晓杰, 蔡莉华

(辽宁师范大学 物理与电子技术学院，辽宁 大连 116029)

双重子奇特态是一类全新的物质结构，其存在与否是检验基本相互作用的理想场所,所以不论理论上还是实验上一直引起物理学家的兴趣和重视. 最近COSY实验第一次证实了非奇异d*双重子奇特态(自旋S=3和同位旋T=0)的存在[1], 使得这一方向的研究又成为该领域的热点[2-3]. 1964年提出的夸克模型理论[4]认为重子是由3个夸克构成, 介子由1个正夸克和1个反夸克构成,夸克模型已经被很多实验证实是相当成功的模型.夸克模型理论预言超过4个夸克构成的多夸克系统即奇特态是存在的，但遗憾的是直到50 a后的2014年德国的COSY实验组才第一次证实d*多夸克奇特态的存在.

目前，人们认为描述强相互作用的基本理论是量子色动力学(QCD),它的性质有：色禁闭、渐近自由和手征对称性.可以利用这一理论处理高能区的微扰论计算, 但是在处理中低能区的非微扰相互作用时仍存在困难.奇特态是否存在可以检验非微扰相互作用，所以人们不得不借助具有QCD精神的唯像模型来处理.笔者提出的手征SU(3)夸克模型是最具有QCD精神的成功模型之一[5-6]. 在这一模型中,单胶子交换提供短程微扰相互作用,色禁闭势提供的是长程相互作用,从夸克与手征标量和赝标量九重态场耦合的拉格朗日量得到中程相互作用且满足QCD理论要求手征变换不变性. 在此基础上进一步引入夸克与矢量九重态场的耦合, 从而提出了推广手征SU(3)夸克模型[7].这两个模型下的短程相互作用机制是完全不同的,手征SU(3)夸克模型短程相互作用机制是单胶子交换,而在推广手征SU(3)夸克模型中是矢量介子交换.共振群方法(RGM)是处理集团之间相互作用的成熟计算方法，本研究组应用RGM方法研究了核子-核子以及核子-超子相互作用.结果表明这两个不同短程相互作用机制的模型都可以合理描述相移和截面等散射实验[6-7].在此基础上,利用相同的模型参数，进一步预言了可能存在的六夸克态d*结构.研究发现手征夸克模型理论预言值与2014年COSY实验结果惊人的一致[8-10], 从而进一步证明了本组提出的手征夸克模型是完全合理和有效的,是描述强相互作用成功的理论模型.分析发现在形成这一奇特态结构中, 除了系统具有特殊的对称性外,重子的新颜色结构也是非常重要的,这就是来自隐色道(CC)的耦合对d*奇特态的形成有很大的影响.

通过研究另一感兴趣d*镜像核(S=0,T=3)态的性质, 发现隐色道效应在形成其奇特结构中也是非常重要的[11-12]. 进一步拓展到奇异夸克系统, 引入奇异重子的新颜色结构, 也发现隐色道效应对某些特殊的系统有很大影响[13-15].显然, 继续深入系统地研究隐色道对不同系统带来的效应是人们感兴趣的也是有意义的重要前沿工作[2-3].本文在文献[14]工作的基础上, 进一步研究不同短程相互作用机制即矢量介子交换机制下,奇异数-1的Σ*Δ系统的自旋S=0态的结构和性质.在推广手征SU(3)夸克模型下对该系统进行了动力学计算.首先，在单道计算下研究了短程矢量介子交换机制下系统的结合能和均方根半径及各种相互作用对系统结合能的贡献;然后，进一步在耦合的隐色道计算下研究Σ*Δ系统是否受到这一效应的影响,得到了一些有趣且有意义的预言结果.

1 理论模型

重子-重子系统的哈密顿量在手征推广SU(3)夸克模型下为

(1)

(2)

两集团构成的系统波函数[8，10]用RGM方法表示

|AB〉=A [φAφBχ(R)Z(RCM)],

(3)

这里A是反对称化算符,φA表示的是集团A的内部运动波函数，φB表示的是集团B的内部运动波函数,χ(R)为集团之间的相对运动波函数,Z(RCM)整个系统的质心运动波函数.为了解析求解, 进一步需要对相对运动波函数χ(R)做高斯基展开. 最后通过变分法,求解双重子系统的薛定谔方程从而得到系统波函数以及能量E.

Σ*Δ双重子的结合能定义为

Eb=-(EΣ*Δ-MΣ*-ΜΔ).

(4)

本文的计算利用了在文献[14]得到的带奇异夸克系统的自旋-味道-颜色-同位旋空间矩阵元结果, 那里详细给出了构造隐色道波函数的方法及计算隐色道矩阵元的具体过程.

双重子Σ*Δ系统S=0时自旋波函数为

(5)

双重子Σ*Δ系统同位旋T=5/2时味道波函数为

(6)

由式(5)和式(6), 最后得到Σ*Δ系统自旋S=0和同位旋T=5/2空间波函数

(7)

在此基础上进一步构造隐色道波函数, 此时需要利用集团之间的反对称化算符

(8)

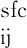
|CC〉=a|Σ*Δ〉+bAsfc|Σ*Δ〉,

(9)

再利用正交关系最后得到

(10)

上面给出了文献[14]中计算自旋-味道-颜色-同位旋空间矩阵元时需要的波函数,利用一种新方法即展开系数法去计算这些矩阵元, 从而避开了与群论和其代数表示相关的所有复杂计算.

2 模型参数

计算中有3个基本模型参数，其余参数取实验值以及运行重子基态的稳定条件得到. 这3个基本参数为夸克波函数的宽度和上夸克质量及奇异夸克质量.夸克波函数取的是谐振子基态波函数, 其宽度大小的合理取值范围在0.45～0.6 fm之间，由实验质子电荷的均方根半径决定.实验可确定夸克-手征场耦合常数.重子的稳定条件给出单胶子交换和禁闭势参数.除了mσ,mκ外,其他手征场质量均取为实验值,对应的截断质量全部为1 100 MeV. 本文计算的模型参数和文献[6-7]取值一致,利用这些参数合理地描述了核子-核子和核子-超子散射相移和散射截面等实验结果. 表1列出了主要模型参数.

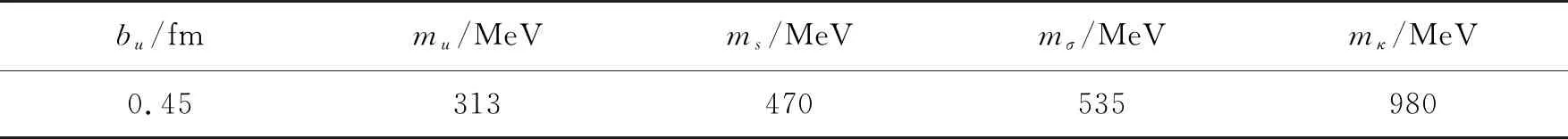
表1 模型参数

3 结果和讨论

文献[9]通过对Σ*Δ(S=0,T=5/2)对称性进行分析, 也就是计算集团间自旋-味道-颜色空间反对称化算符的期待值, 发现双重子Σ*Δ系统间夸克交换效应很明显, 可以使两集团间的距离非常近, 从而有利于形成多夸克态结构.

两个重子构成的系统, 最后能否形成双重子束缚态结构, 还需要进行动力学计算.在推广手征SU(3)夸克模型下, 利用表1模型参数, 分别对单道和耦合道情况下奇异数为-1的Σ*Δ系统的结合能和均方根半径进行研究, 表2给出计算结果.

表2 Σ*Δ系统的结合能和均方根半径

从表2可以得出:单道和耦合道的计算均可以使Σ*Δ形成束缚态. 单道计算的结合能为20.2 MeV,均方根半径为1.0 fm; 耦合道计算的结合能为24.4 MeV,均方根半径为0.96 fm. 可以看到加入隐色道后,Σ*Δ态的结合能增加了4.2 MeV.

表3进一步可以给出各个相互作用对双重子Σ*Δ系统结合能的贡献,表中的数据前正号表示吸引效应, 负号表示排斥效应. 从单道的贡献可以看出: ρ和ω矢量介子交换项及π介子交换提供主要的排斥贡献, 单胶子交换OGE的排斥贡献很小, 可以忽略. 和文献[14]进行对比, 发现在推广手征SU(3)夸克模型下矢量介子交换项机制对Σ*Δ系统的影响取代了手征SU(3)夸克模型下的单胶子交换机制的影响. 从表3还可以看出主要的吸引贡献是由动能和σ介子交换提供. 在考虑隐色道耦合效应后禁闭势发生变化, 这一点可以理解，因为禁闭势项算符是颜色相关的[6-7]. 从表3中还可以得到, 加入隐色道后系统的动能变化很大, 使得夸克交换效应增强, 从而更有利于束缚态的形成.

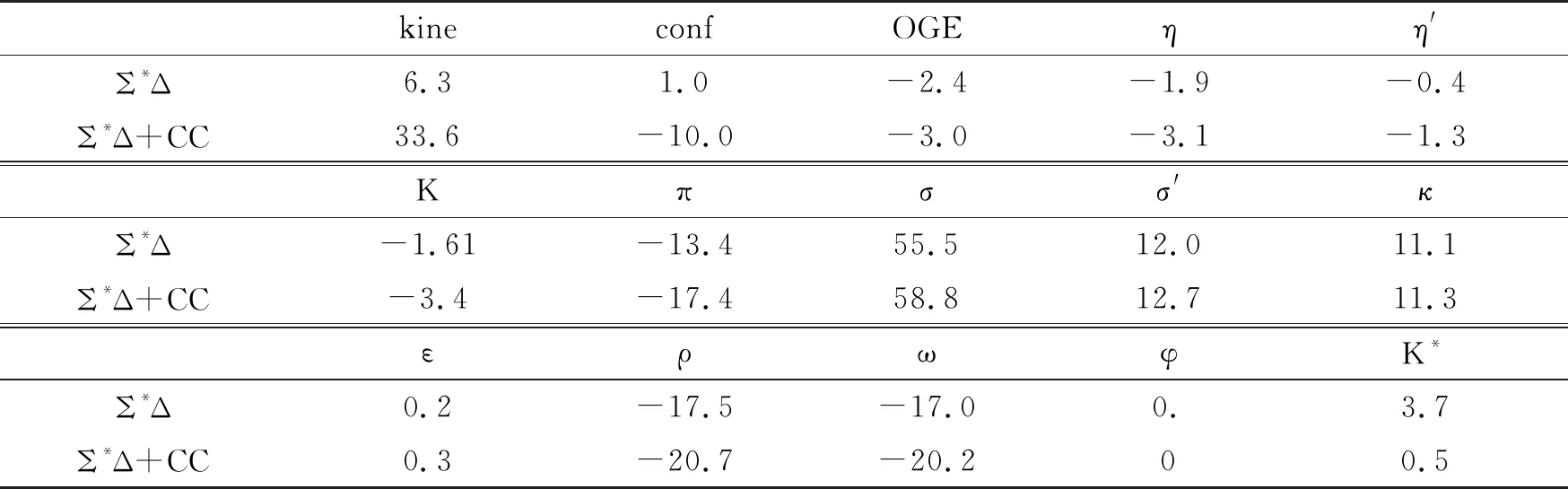
表3 各种相互作用对Σ*Δ系统的结合能的贡献

文献[14]手征SU(3)夸克模型下的计算结果可以看到:不论单道还是耦合道下的计算,Σ*Δ均可以形成束缚态.单道的计算给出的结合能为32.2 MeV,耦合道结合能为39.5 MeV,加入隐色道后会使Σ*Δ态的结合能增加7.3 MeV.和本文推广手征SU(3)夸克模型下的计算结果相比,手征SU(3)夸克模型下隐色道效应更为明显.这一点不难理解,矢量介子交换算符和颜色无关,而单胶子交换算符和颜色有关.

综上所述,本文在推广手征SU(3)夸克模型框架下,应用共振群方法,对奇异数为-1的双重子Σ*Δ系统的结构和性质进行了研究.首先，给出双重子Σ*Δ在单道下的计算结果.接着考虑了隐色道效应,进一步研究隐色道计算下系统的结合能等性质.结果说明:单道和耦合道这两种情况下，均可以使Σ*Δ形成束缚态.系统在考虑隐色道的耦合后,结合能增加4 MeV左右,使双重子Σ*Δ变得更为束缚.但是,和手征SU(3)夸克模型下的结果相比较,发现矢量介子交换机制下的隐色道效应没有单胶子交换机制下明显.

本文是目前强子物理领域感兴趣的前沿方向,预言多夸克奇特态系统是否存在是研究热点.正如前面提到的,本组工作提供了一种构造隐色道波函数和计算相关矩阵元的新方法,这一方法能避开复杂的群论相关计算是非常重要的.