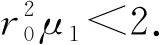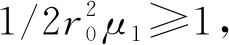非自治强衰减波动方程的适定性

韩英豪， 温 馨， 崔晓旭， 周雪莹

(辽宁师范大学 数学学院，辽宁 大连 116029)

本文考虑如下非自治阻尼强衰减波动方程：

(1)

其中，s∈,n∈,n≥3,Ω⊂n是具有光滑边界∂Ω的有界开区域.假设非线性项f：→为连续可微，存在常数c>0，满足条件：

|f′(z)|≤c(1+|z|p)，z∈，

(2)

并且，外力项满足条件：

‖G(·,t)‖L2(Ω)≤c(1+tp+1),t∈.

(3)

β0≤β(t)≤β1,∀t∈.

(4)

函数r:→+为一致Hölder连续，连续可微，存在正常数0

r0≤r(t)≤r1,∀t∈.

(5)

当n=1,r(t)≡1时，此方程是黏性介质中的均匀弦的横向震动和均匀杆的纵向震动的数学模型.其中，强衰减项-Δut表示系统所受到的与形变成正比的应力，对系统构成一种衰减因素.当n=3时，此方程是各向同性的、均匀的、具有较短记忆的线性黏弹性固体震动的数学模型，对自治情况的此类方程有不少学者进行过研究[1-4].其中,文献[1]研究了自治情况下的此类方程的整体解的存在性、渐近衰减性和ω-极限集的性质等.本文将研究非自治状态下的上述方程的局部与整体解的唯一存在性和关于初始条件的连续依赖性.为此，需要如下非自治发展方程理论.

定义1[5]设X是一个Banach空间，B(t):D⊂X→X，t∈[t0,T](D为与时间无关的集合)是闭的稠定线性算子.

(a)算子族B(t)称为一致扇形算子，如果∀t∈[t0,T],Re(λ)≥0，(λI+B(t))-1存在，并存在常数M>0，使得

(b)B(t)为一致Hölder连续.也就是说，存在常数L>0,1≥α>0,对任意t,τ,s∈[t0,T],有

定理1[5]如果Banach空间X上的一个算子族B(t),t∈[t0,T]满足定义1中的条件(a)与(b),那么在[t0,T]×X上存在唯一发展过程V(t,s):X→X,对任意t0≤s≤t≤T,满足

(i)‖V(t,s)‖L(X)≤C.

(ii)V(t,s)X⊆D,并t→V(t,s)是在X上强可微，其导函数Vt(t,s)∈B(X)(B(X)为X中的所有有界子集构成的集族)，并Vt(t,s)在t0≤s

并且

(iii)对任意x∈D,t∈[t0,T],V(t,s)x在t0≤t≤T上关于s可微，并且

下面考虑Banach空间X上的柯西方程：

(6)

其中,B(t)为定义1中的线性算子.

定理2[5]假设方程(6)中的B(t)为一致扇形算子，一致 Hölder连续,F(t,x)∶[t0,T]×X→X是关于t连续.关于x一致Lipschitz连续.那么,对任意x0∈X,存在唯一x∈C([t0,T]∶X),使得

把x(t)叫作方程(6)的温和解.进而，x0→x是从X到C([t0,T]∶X)的Lipschitz连续映射.

如果f∶[t0,∞]×X→X关于t≥t0连续，在[t0,∞)的有界区域上一致Lipschitz连续，那么存在tmax>t0,方程(6)在[t0,tmax]上存在唯一温和解x(t).如果tmax<∞,那么

如果f为连续可微，那么温和解就是古典解.

1 方程(1)的适定性

(7)

从而，方程(7)的线性部分和非线性部分为

那么，方程(7)生成的演化过程{U(t,s)|t≥s}满足如下积分方程，因而可分解成:

C(t,s)ws+S(t,s)ws.

(8)

的解所生成的V上的演化过程.

此外，把算子分解为Aβ(t)=A1(t)+A2(t),其中,

引理1对任意t∈,算子A1(t)是闭的，最大耗散的，而且0∈ρ(A1(t)).其中,ρ(A1(t))是A1(t)的预解集.

证由于A闭的,因而A1(t)是闭的.另外,一方面由于对任意(u,v)∈VD(A1),有

是方程

(

的唯一解.这就证明了A1(t)是耗散的.

最后，由于算子A1(t)的逆算子是

因而,0∈ρ(A1(t)).证毕.

引理2算子族A1(t)为在V中是一致扇形正定算子.

证如果令Π(λ)=λ2I+λr(t)A+A,那么A与Π(λ)可交换，而且A1(t)的预解算子R(λ,A1)=(λI-A1)-1为

其中,Re(λ)>0.

下面将证明存在正常数C(r1),Cr0,r1,使得

(9)

(10)

(11)

首先证明式(10).由Π(λ)的定义，有

因此,对于任意的x∈X,对于任意Re(λ)>0,有

(12)

而且,由式(12)可知，对任意Re(λ)>0,算子Π(λ)A-1/λ是单射的,Π(λ)A-1/λ的值域是整个空间X.因此,对任意Re(λ)>0,式(10)就成立.

其次证明式(9).由Π(λ)的定义，有

(13)

因此,对于x∈D(A),可推出

(14)

(15)

因此，由式(14)和式(15)可得

因此，在假设情况(a)下，式(9)就得到了证明.

(16)

对于任意Re(λ)>0成立.因此,在(b)情况下,同样证明了不等式(9).

最后证明式(11):由式(14)有

Π(λ)A-1=I+r(t)λ+λ2A-1=I+r(t)A1/2(λA-1/2)+(λA-1/2)2.

在不等式(9)证明中从式(13)得到式(16)的过程中，把(λA-1/2)用(A1/2/|λ|)来替代.那么，对任意x∈X,有

2Re((λA-1/2)2x,x)+2r(t)(Re(λ))(‖x‖2+‖λA-1/2x‖2)>0, ∀Re(λ)>0.

(17)

其中,Re(λ)>0.这就证明了式(11).

根据以上的估计式(9)～式(11),存在常数Cr>0,对任意λ,当Re(λ)>0时,对任意x∈X,预解算子R(λ,A1)X有如下估计式:

这就得出了引理2结论.证毕.

定理3对任意r>0,以及s∈,存在α,τ>0,对任意w0∈V,=w0=V≤r,存在方程(8)的唯一解w,使得w(·,s,w0)∈C([s,s+τ],V)∩C1((s,t0+τ],V′).并且，如下映射是连续的:

{w0∈V:‖w0‖V≤r}w0w(·,s,w0)∈C([s,s+τ],V).

证根据引理(2)以及假设条件(4)和假设条件(5),算子A1(t)是一致扇形的，并且算子A2(t)是关于t一致有界的，且

由r(t)与β(t)的一致Hölder连续性，存在w>0，使得

=[Aβ(t)-Aβ(s)]Aβ(t0)-1=L(V)≤M|t-s|w.