一种GNSS非接触式地理信息采集方法与装置
2020-12-29方田野郭际明邹进贵
方田野,章 迪,郭际明,邹进贵
(武汉大学测绘学院,武汉 430079)
近年来,以GPS和北斗为代表的GNSS技术在各领域得到了广泛应用[1].它提供了一种实时、动态、精确获取空间数据的方法,是地理信息采集的重要手段[2].然而,现有的GNSS测量方法均为接触式,即要求将GNSS接收机置于待定点的正上方(利用对中杆、基座或三脚架),若待定点的观测环境较差或因条件限制无法安置GNSS接收机时,就会导致待定点测量误差达不到精度要求甚至无法进行测量(以下统称为“GNSS盲点”).
为得到GNSS盲点的坐标,通常将全站仪与RTK相结合[3-5],即在其附近选择至少两处GNSS观测条件较好的位置,用RTK方法测出坐标作为已知点,然后在其中一个与GNSS盲点通视的已知点上架设全站仪,瞄准另一个已知点进行定向,最后再利用极坐标法测得GNSS盲点的坐标.此方法的缺点在于:1) 全站仪附件较多,不易携带;2) 全站仪的对中整平耗时耗力;3) 已知点位间必须通视,但又不能距离太近,否则定向误差很大[6];4) 全站仪造价较高,通常在数万元.超站仪将GNSS接收机和全站仪整合为一体进行测量[7],其实质也是利用了这种方法.目前市面上还有一种带有MEMS传感器的GNSS接收机,可在不进行严格整平的情况下实现小范围的倾斜测量[8],它具有以下缺点:1) 内置惯性传感器准确度和精度有限,需要经常校准,且校准后仍然误差很大;2) GNSS接收机能离开GNSS盲点的范围受限于对中杆长度;3) 系统造价较高.
总的看来,现有的“非接触式GNSS测量”本质上都需要依靠角度观测值.为此,本文给出一种GNSS与激光测距相结合的测量方法及装置,以弥补现有技术在效率、成本、精度等多方面的缺陷.
1 数学模型
设GNSS盲点坐标为(x,y,h),其周围有n个辅助点,任一辅助点坐标记为(xi,yi,hi)(i=1,2,3,…,n),激光测距仪到已知点的高度记为ΔHi,到GNSS盲点正上方Δhi处的斜距为Si,则有:
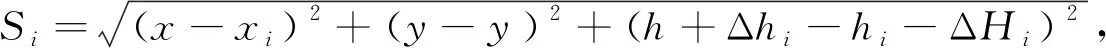
(1)
式(1)为三元二次方程,需要已知3个以上辅助点的三维坐标,以及辅助点与GNSS盲点之间的斜距求解.当只有3个辅助点时,一般可求解出两组满足要求的坐标,此时可根据GNSS盲点的近似高程进行筛选[9],但近似高程的确定并非易事;利用点号的编排法则也能唯一确定GNSS盲点的三维坐标[10],但其实质是要求知道GNSS盲点与3个辅助点构成的平面之间的位置关系,此关系在实际测量中很难判断.因此可使用多于3个的辅助点来确定GNSS盲点坐标,下面给出数学模型.
式(1)的误差方程为:
Vi=cδx+diδy+eiδh-li,
(2)
其中,
li=Si-S0,
(x0,y0,h0)为待定P点近似坐标,(xi,yi,hi)为第i个已知点的三维坐标,
S0=
根据最小二乘可得:
(3)
式中,
水平精度因子
垂直精度因子
2 装置与方法
2.1 硬件装置
依据上述原理,在现有RTK设备的基础上,设计了一特制夹具,能将激光测距仪固定在对中杆上,形成了一套低成本、易携带的硬件装置.如图1所示,所述特制夹具包含一个万向头,使得测距仪可以根据需要灵活地指向目标点,同时夹具可以沿对中杆上下滑动,测距仪距已知点的高差(式(1)中的ΔHi)可通过对中杆的刻度值进行换算.

图1 硬件装置构成示意图Fig.1 Diagram of hardware device structure
2.2 使用方法
使用该装置进行测量的流程如图2所示,主要步骤如下.
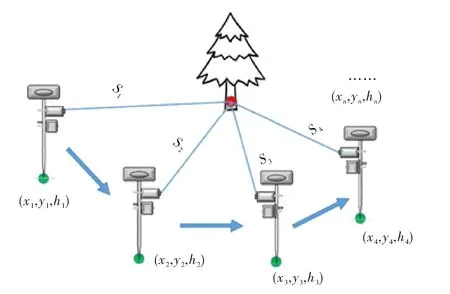
图2 测量流程示意图Fig.2 Diagram of the surveying method
1) 在GNSS盲点的附近选择几个GNSS观测条件较好、与GNSS盲点通视、且分布较为均匀的位置,作为辅助点;
2) 在辅助点上进行RTK测量,得到三维坐标;
3) 在辅助点上,利用激光测距仪瞄准合作目标上的合适位置测出斜距,如有遮挡,可沿对中杆上下滑动调整激光测距仪的高度ΔHi(可通过读取对中杆上的刻度值进行换算),以及激光光斑到GNSS盲点的高度Δhi(可利用卷尺量取,如图3所示);
4) 移动到下一个辅助点,重复步骤2)至3);
5) 当观测了至少4个已知点时,使用式(3)计算GNSS盲点坐标和精度信息.

图3 激光测距仪光斑高度Fig.3 The height of spot
3 实验结果及精度分析
3.1 模拟实验

为研究辅助点数量及其分布对交会定位的影响,先模拟50种交会情形,其中辅助点数量的变化范围为4~8个,距GNSS盲点水平距离变化范围为2~30 m、垂直距离变化范围为1~10 m,使HDOP与VDOP设计值在0~25 区间,其中HDOP和VDOP的设计值利用辅助点设计坐标与距离真值代入(3)式计算得到.图4给出了三种典型的交会情形.对每种交会情形进行3 000次模拟实验,每次实验时对辅助点设计坐标值和距离加入服从标准正态分布的随机误差,其中辅助点坐标在x、y方向上的中误差均设置为±2 cm,在h方向上的中误差设置为±5 cm,测距中误差设置为±(1.5 mm+1 ppm).GNSS盲点的交会结果散点图如图5所示.
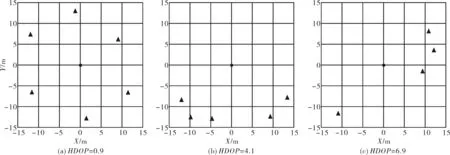
图4 点位分布示例图(平面)Fig.4 Sketch map of point distribution(plane view)

图5 交会结果散点示例图 (平面)Fig.5 Examples of scatter plot of intersection results(plane view)
由图4、图5可知,辅助点分布越均匀则HDOP越小.当HDOP小于5时,△x与△y绝大部分在5 cm以内;当HDOP大于10时,点位精度变差.可见,优化图形结构、增加辅助点数量,可减小HDOP,提高定位的平面精度,高程的情况类似.
实验中发现,对于某一特定交会情形,虽然其3 000次模拟实验中HDOP设计值保持不变,但每一次平差所得的HDOP却不尽相同.将每种交会情形的HDOP的标准差统计如表1所示.
由表1可知,HDOP设计值小于10时,标准差接近于0,说明实际平差得到的HDOP与其设计值吻合很好;但当设计值大于10时,开始变得不稳定.这是因为,辅助点分布的图形结构差,观测值误差的小变化会导致平差结果大的变化.因此在实际测量过程中,应尽量避免HDOP值大于10的情况.
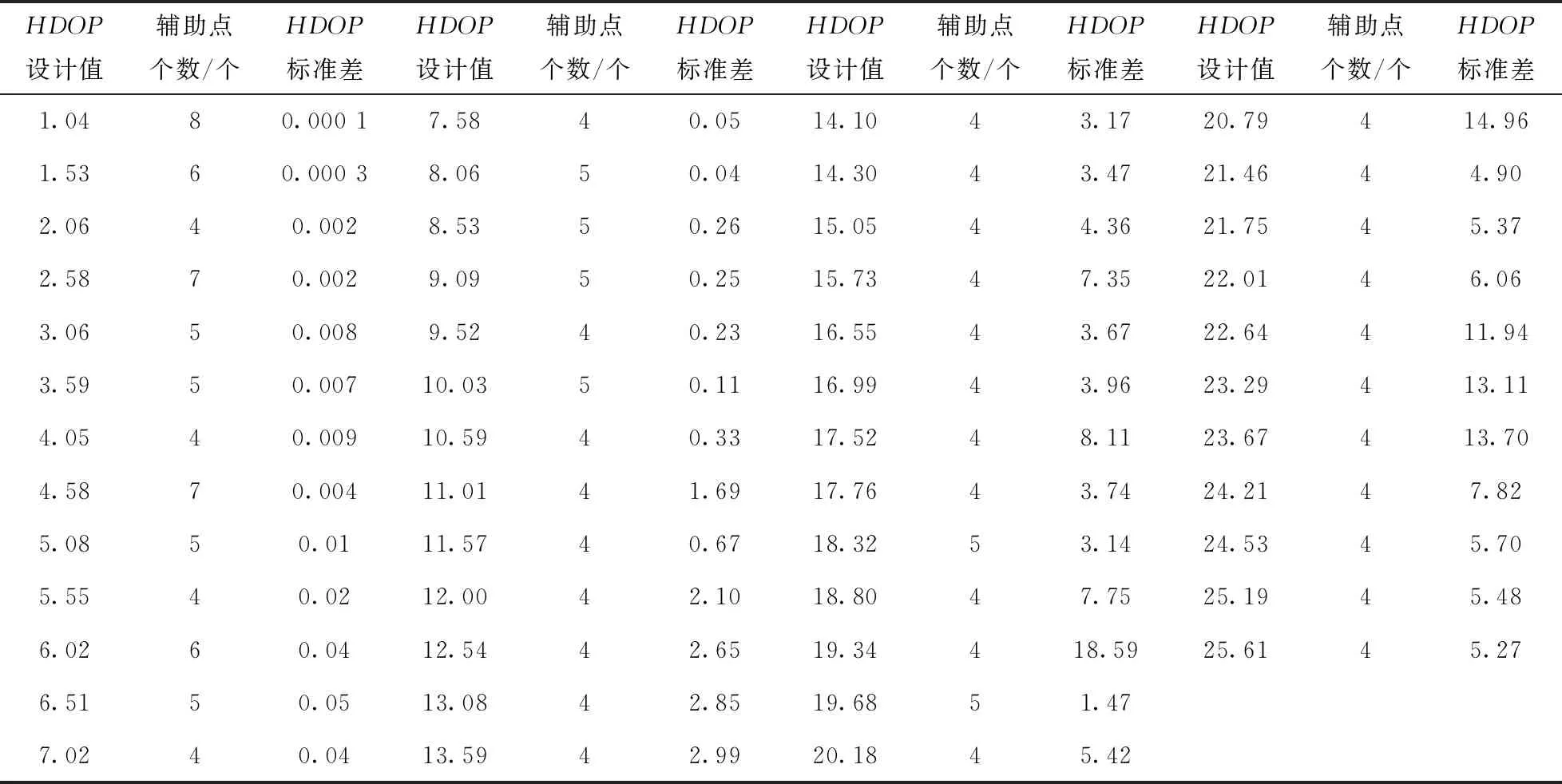
表1 HDOP设计值与平差所得HDOP标准差统计表Tab.1 Statistics table of HDOP between designvalue and standarddeviation
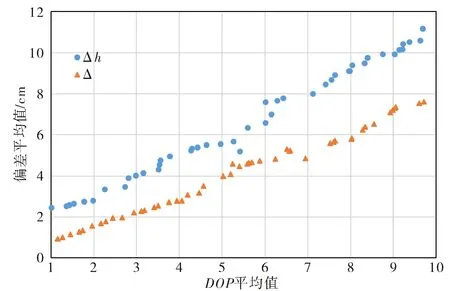
图6 点位偏差均值与DOP关系图Fig.6 Relation between average error and DOP
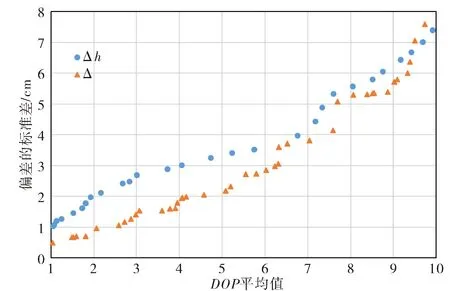
图7 点位偏差标准差与DOP关系图Fig.7 Relation between standard deviation and DOP
m△=0.613×HDOP
m△h=0.682×VDOP
二者的比例系数较为接近,对照式(3),可知此处的比例系数应为单位权中误差σ0的估值.由此进一步印证了,在观测精度一定时,辅助点的分布越好,定位精度越高.在实际测量中,应使辅助点在平面和高程上都尽可能均匀分布.
3.2 实地实验
实验地点位于武汉大学信息学部,表2列出了实验中所用到的仪器型号.以如图8所示的松树树干根部作为GNSS盲点.首先选择两个距离较远且观测条件较好的点,利用RTK测出坐标;之后用全站进行设站、定向,测出松树的坐标作为参考值;然后在松树周围选择8个辅助点,根据前述方法进行交会计算.得到的原始测量数据如表3所示.
选取不同数量、不同分布的辅助点进行交会计算,以全站仪测量得到的坐标P(3378714.266,534185.891,20.509)作为松树坐标的参考值,统计不同方案的定位精度如表4所示.
根据表4可知:1) 平面、高程偏差均和位置精度因子之间呈正相关;2) 高程精度整体偏大,这是因为实地地形限制,辅助点间高差较小,导致VDOP偏大;3) 在辅助点分布均匀、数量足够时,可获得与直接利用RTK测量相当的精度.这与前述模拟实验的结论一致.

图8 实地实验场景图Fig.8 The scene graph of the field experiment
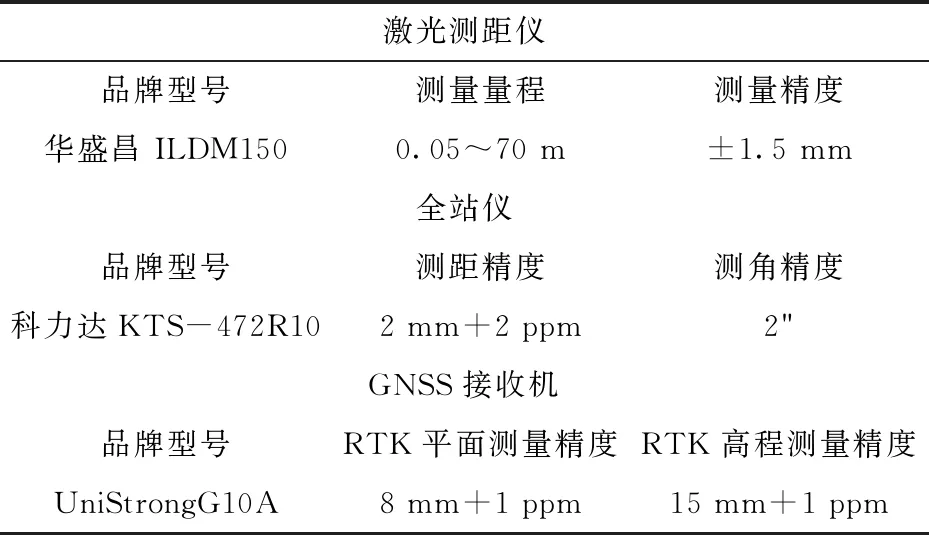
表2 实验用测量仪器参数
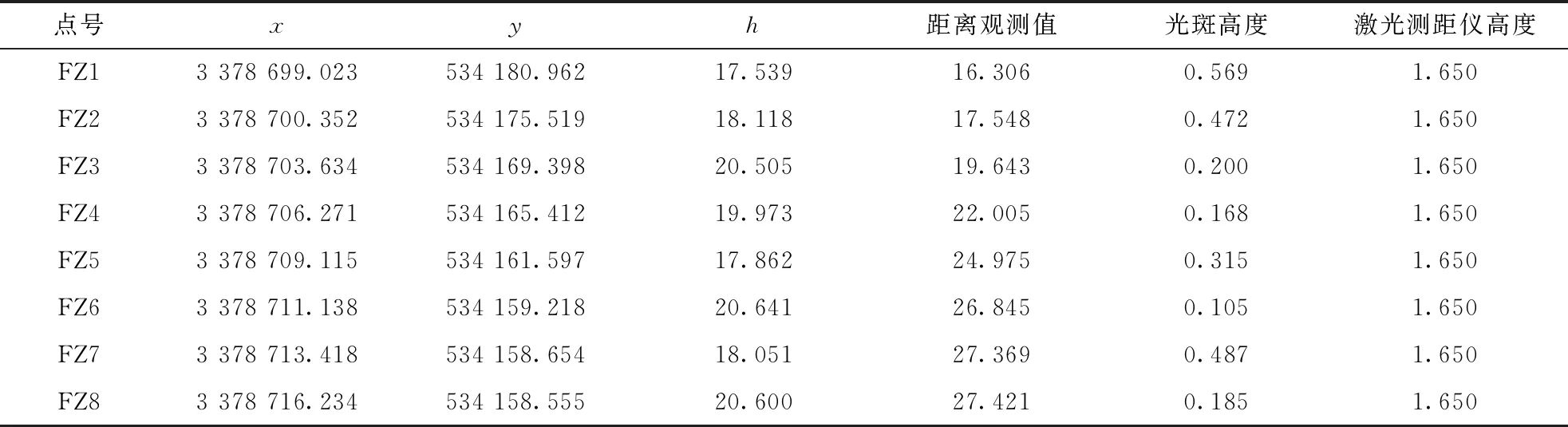
表3 实地实验原始观测值Tab.3 Original observation of field experiment m

表4 实地实验精度统计Tab.4 Accuracy statistics of field experiment cm
4 结语
在观测精度一定时,交会定位的精度主要取决于DOP的大小.为保证交会定位的精度和可靠性,HDOP和VDOP值均应控制在10以内.实际测量中,DOP可通过平差计算得到,辅助点是逐个测量的,当辅助点数量达到4个时,即可进行平差计算,根据平差后的DOP值及中误差决定是否继续增加辅助点或调整辅助点的分布.
本文所采用的非接触式GNSS测量方法,摆脱了定位对角度观测值的依赖.所述装置成本低廉、便于携带,方法操作简便,并已获得中国专利授权[11],模拟和实地实验数据均表明,利用GNSS盲点30 m范围内数量足够、分布均匀的辅助点,可获得与RTK直接测量相当的精度,可作为常规方案的有益补充.
