基于混合协同过滤的个性化推荐方法研究

孙传明，周 炎*，涂 燕

(1.华中师范大学国家文化产业研究中心，武汉 430079； 2.武汉理工大学安全科学与应急管理学院，武汉 430070)

互联网的迅速发展带来了信息的飞速增长，同时也给人们带来了“信息过载”[1]的困扰性问题.推荐系统的产生在一定程度上解决了该问题，并且随着个性化推荐技术的发展，推荐系统的推荐质量也得到有效提升.在个性化推荐领域中，基于协同过滤(Collaborative filtering，CF)的推荐算法逐渐成为研究热点，并被广泛应用[2].目前传统的协同过滤算法存在数据稀疏性问题和推荐范围问题，其中数据稀疏问题会导致相似度计算的不准确，推荐范围问题会影响最终的推荐结果质量.许多学者也针对这些问题对传统的协同过滤算法进行了改进，周超等针对用户-项目评分矩阵进行横纵聚类，并且提出杰卡德系数和皮尔逊相关系数结合的相似度计算方法[3].郭雷等将用户或项目的共同评分项数量引入相似度计算中，利用控制因子将两种推荐算法结合并产生最终推荐[4].时念云等合理量化了影响信任的相关因素，并建立以及优化多元信任模型，以信任度取代相似度，考虑了用户信息[5].李丹等提出基于读者用户画像构建方法，将具有相同特征的用户划归成一类，给出个性化推荐方案[6].Kang引入用户信任相似度以及基于加权信息熵的相似度作为最终的用户相似度[7].YUAN等提出了多级混合相似度，依据用户等级的数量动态整合用户兴趣相似度和用户的特征相似度[8].这些算法主要对用户的相似度进行优化，考虑了影响用户相似度计算的多种因素，或者充分利用用户-项目评分矩阵生成横纵聚类集，但未充分考虑项目本身具有的属性特征以及与其相关的外部信息.

针对当前数字信息资源与日俱增的背景，本文结合两种传统的协同过滤算法，提出一种混合的协同过滤方法，并以电影评分的数据集MovieLens作为实验数据，完成了与传统算法的对比实验和关于权重因子的灵敏度分析，以证明方法的有效性.

1 传统的协同过滤算法

基于用户(User-based)和基于项目(Item-based)的协同过滤算法是传统算法中比较典型的两种[9]，均包括三个部分：用户行为[10]表示、邻居用户/项目选择以及产生推荐[11].

1.1 用户行为表示

用户行为是指在各大平台网站上，从用户进行相关搜索到用户停止相关搜索而产生的一系列用户操作.用户行为主要采用用户-项目评分矩阵来表示，该矩阵记为R(m，n)，如公式(1)所示.其中，m为行数，表示用户数，n为列数，表示项目数，矩阵中的第i行第j列(即Rij，1≤i≤m,1≤j≤n)表示用户i对项目j的评分.

(1)

为便于计算和理解，评分值通常是对原有数据处理之后形成的数字指标，数值大小代表了用户对项目的满意/喜爱程度.用户i对项目j的评分定义公式为：

(2)

1.2 邻居用户/项目的选择

1)相似度计算

将用户对项目的评分集合表示为一个向量(即公式(1)所示矩阵中的某一行/列数据)，计算向量相似度得到用户/项目间的兴趣偏好相似性，相似度越高可认为用户/项目间的兴趣偏好较一致.本文采用余弦相似度(Cosine-based Similarity)来计算用户相似度以及项目原始相似度.以用户相似度为例，其计算公式如下：

(3)

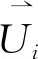
2)选择最近邻

本文采用k最近邻选择法[12]，选择相似度较高的前k个用户/项目，这k个用户/项目便组成了目标用户/项目的最近邻Ni.

1.3 产生推荐

1)基于用户的协同过滤算法中，利用预测评分法产生推荐

首先，对未评分项目计算预测评分Pui，计算公式如下：

(4)

其次，根据公式(4)计算的预测评分，将分值较高的N个项目推荐给目标用户.

2)基于项目的协同过滤算法中，利用权重求和法产生推荐

对项目j的预测评分Puj进行计算，计算公式为：

(5)

其中，Rui代表项目i在目标用户u上的评分，Nj表示项目j的最近邻.利用公式(5)进行计算可以使预测值在分值定义的范围内.

2 基于用户-项目的混合协同过滤推荐

传统协同过滤算法仅依靠评分相似度进行推荐，本部分考虑了除评分相似度以外的项目标签属性相似度，不仅可以充分利用项目信息，也能够有效改善数据稀疏性并提高推荐的精确性.项目综合相似度的计算方式以及该方法的计算步骤如图1所示，该方法主要通过两步形成最终推荐，首先针对原始用户-项目评分矩阵中的零值，利用基于项目的协同过滤算法进行评分预测；其次是利用基于用户的协同过滤算法对替换零值后的评分矩阵进行评分预测并形成推荐.

2.1 混合协同过滤中改进的项目相似度计算

在混合协同过滤算法中采用皮尔逊相关系数来计算任意两个项目i和j的评分相似性，其中，Uij=Ui∩Uj，代表对项目i和项目j已评分的用户集合.此相似度计算公式为：

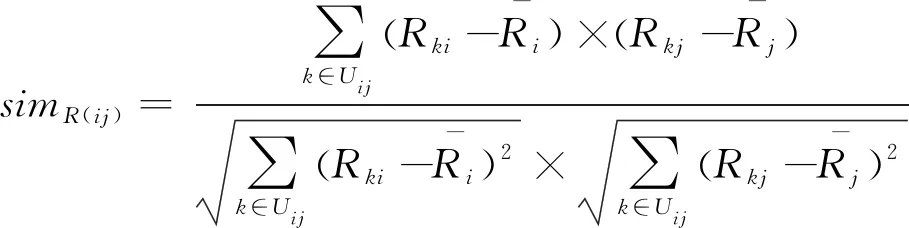
(6)

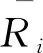
1)建立项目标签属性矩阵I(m，n)，其中m行表示m个项目，n列代表n个标签属性，矩阵中的第i行第j列(即Iij，1≤i≤m,1≤j≤n)表示项目i是否拥有标签属性j.一般Iij=0或1，表示项目i不具有/具有标签属性j.

(7)

2)计算项目标签属性相似度

项目标签属性相似度可以表示为：

(8)

其中，Nij表示项目i和项目j都具有的标签属性数量，Nc表示标签属性的总量，Nn表示既不属于项目i也不属于项目j的标签属性数量.公式(8)即杰卡德系数计算方法.

最后引入权重因子λc[13](表示项目属性的权重)，如公式(9)：

(9)

混合相似度的计算公式为：

simij=λc*simc(ij)+(1-λc)*simR(ij).

(10)

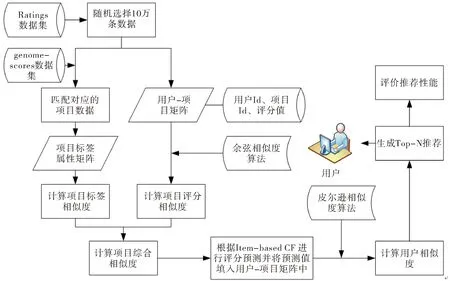
图1 混合协同过滤推荐流程图Fig.1 Hybrid collaborative filtering recommendation flowchart

2.2 混合协同过滤推荐方法的计算过程

和传统协同过滤算法的计算过程类似，该方法的计算过程可以分为以下四个步骤：输入用户-项目评价矩阵、选择相似项目集、选择最近邻居集合以及产生推荐[14].

1) 输入用户-项目评价矩阵

输入用户-项目评分矩阵R(m，n)，其中，m行代表有m个用户，n列代表有n个项目，矩阵中的第i行第j列(即Rij，1≤i≤m,1≤j≤n)表示用户i对项目j的评分.若用户i未对项目j评分，则Rij为空值.

2)选择相似项目集

(1)建立如公式(7)所示的矩阵，利用公式(8)计算出相应的相似度，接着采用公式(10)计算项目综合相似度.

(2)根据项目综合相似度选择相似项目集.例如，对于项目a，在整个项目集中选择与项目a相似度最高的N个项目作为项目a的相似项目集，假设相似项目集为SIa.

3)选择最近邻居集合

(1) 填充用户-项目评分矩阵

对目标用户v未评分的项目a，通过项目a的相似项目集SIa，来预测用户v对项目a的评分Pva，计算公式为：

(11)

依据公式(11)，对原始评分矩阵进行填充，直到用户v对所有项目均有评分.

(2) 计算用户相似度

对于填充后的用户-项目评分矩阵，利用皮尔逊相关系数计算目标用户v和用户i之间的相似度simvi，计算公式为：

(12)

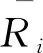
(3)选择最近邻居集合

在整个用户集中，选择与用户v相似性最高的前k个用户作为最近邻居集合Nv.

4)产生推荐

将目标用户v对项目j的评分预测记为Pvj，其计算公式为：

(13)

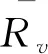
计算用户v对每个项目的预测评分之后，选择预测评分最高且属于用户未评分项目集中的N个项目作为Top-N推荐集.

3 实验与分析

3.1 数据采集与处理

本实验将采用MovieLens 20M数据集进行分析，此数据集描述了5星之内的电影以及相应的标记，适用于对用户进行推荐.数据集包括了138 493个用户，27 278部电影，20 000 263个评分值和465 564个标签，每名用户都至少评分了20部电影，分值介于1～5之间，且分值增量为0.5.此数据集的收集时间为1995年1月到2015年3月.

本部分主要利用ratings数据集(见表1)和genome-scores数据集(见表2)，并且在ratings数据集中选取100 000条评分数据作为实验的数据集，其中包括702名用户和8 227部电影.在设计算法时将数据集按8∶2的比例划分训练集和测试集.该实验测试集的用户评估矩阵稀疏度为：1-100000/(702×8227)=0.983，表示在该用户评估矩阵中，零值的比例达到了98.3%，即该矩阵数据特别稀疏.

ratings数据集如表1所示，包括userId、movieId、rating以及timestamp四种数据.其中userId是指每个用户的id，movieId是指每部电影的id，rating是指用户评分.

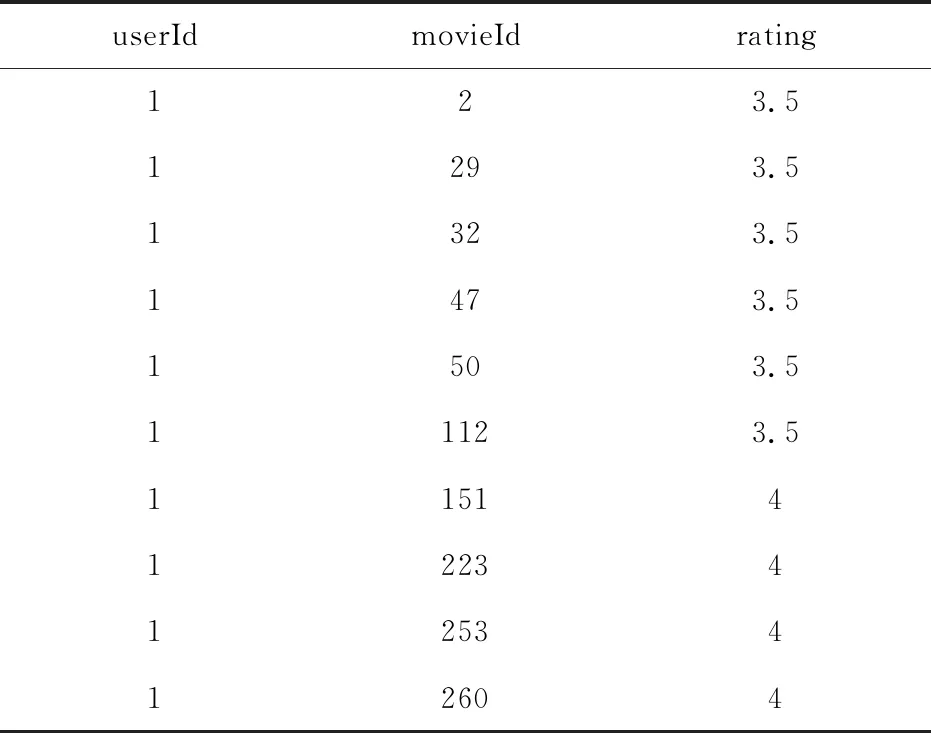
表1 ratings数据集示例Tab.1 Example of ratings dataset

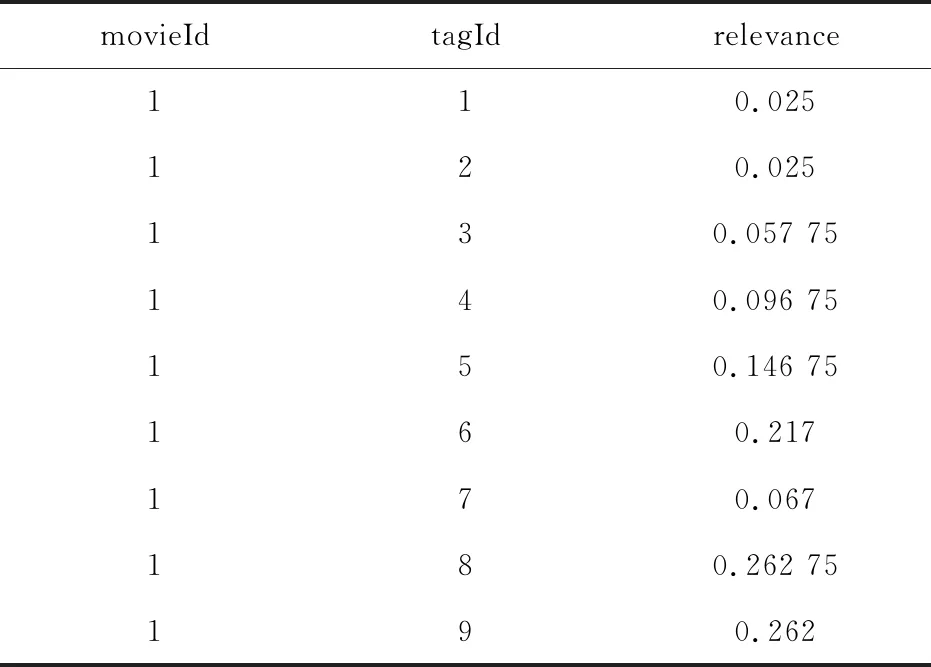
表2 genome-scores数据集示例Tab.2 Example of genome-scores dataset

genome-scores数据集如表2所示，包括movieId、tagId以及revelance三种数据.其中movieId是指每部电影的id，tagId是指电影标签，revelance是指电影与标签的相关性.

在实现算法时，将genome-scores数据表转化为0～1矩阵，将relevance值分为0～0.5和0.5～1两个区间，relevance值若在0～0.5区间则视为项目不具有该标签属性，在0.5～1区间则视为项目具有该标签属性.

3.2 评价指标

本部分主要采用平均绝对误差和均方根误差两种指标进行评价.

1)平均绝对误差

本部分采用的精确度量化指标是平均绝对误差(Mean Absolute Error，MAE)[15].该指标能较好地反映预测值误差的实际情况，计算公式如下：

(14)

其中，n代表整个项目集中已有评分的项目数量，rα代表项目的实际评分，vα代表项目的预测评分.比较不同算法的MAE值，MAE值较小则表示预测误差较小，更能反映实际情况.

2)均方根误差

本部分还采用了均方根误差(Root Mean Square Error，RMSE)[16]，该指标用来衡量观测值同真值之间的偏差，即数据的离散程度，计算公式如下：

(15)

其中，n、rα与vα的含义与公式(14)相同.比较不同算法的RMSE值，RMSE值越小则表示预测精确度越高.

3.3 实验步骤

本次实验采取独立实验和对比实验的方法，选取的用户/项目邻居集的数值(即k值)为10、20、30、40、50、60、70、80、90、100.

实验1：基于混合协同过滤方法与传统算法的对比实验

1) 采用两种传统的协同过滤算法，得到相应推荐结果.

2) 采用混合的协同过滤方法，得到相应推荐结果.

3) 比较3种推荐结果的MAE值和RMSE值.

实验2：基于混合的协同过滤方法的灵敏度分析实验

1) 将权重因子分别设置为0.3、0.5、0.7、0.9，采用混合的协同过滤方法计算，得到相应推荐结果.

2) 采用原始权重因子的混合推荐方法计算，得到相应推荐结果.

3) 比较不同权重因子下推荐结果的MAE值.

3.4 实验结果分析

确定了实验内容之后，利用Python编程语言设计实现3.3节中的两个实验，输出相应结果并进行分析.

1) 基于混合协同过滤方法与传统算法的对比

实验1结果：在不同最近邻个数下，比较基于传统与基于混合的协同过滤方法的MAE值和RMSE值，实验结果如图2和图3所示.

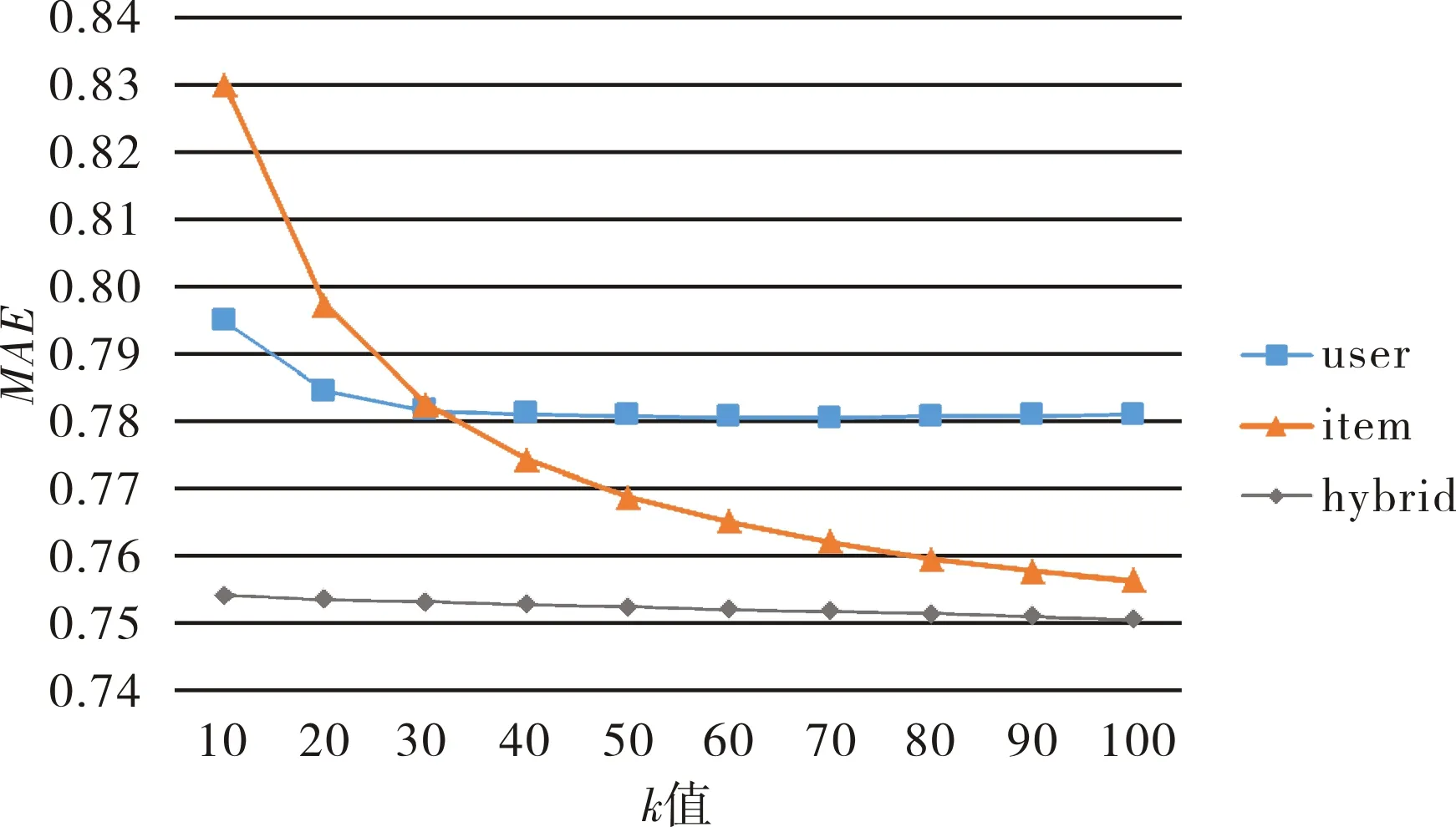
图2 不同方法中k值对MAE值的影响Fig.2 Effect of k value on MAE value in different algorithms

从图2可以看出，基于用户的协同过滤算法的MAE值均在0.78附近，基于混合的协同过滤方法的MAE值均在0.75附近，比前者的MAE值均降低了3%.而基于项目的协同过滤算法的MAE值变化幅度较大，均大于混合的协同过滤方法的MAE值.在基于项目的协同过滤算法中，MAE值变化幅度较大的原因可能是因为计算项目相似度时，项目数量较为稳定，算法对k值的变化较为敏感.在预测评分填充矩阵时，引入项目标签属性相似度，充分利用有效信息，在计算项目相似集方面提高了准确度，说明基于混合的协同过滤方法产生的推荐更加符合用户需求，在一定程度上可以达到提高推荐质量的目的.

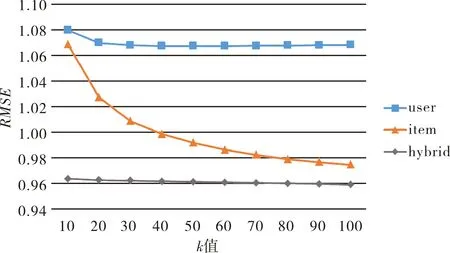
图3 不同方法中k值对RMSE值的影响Fig.3 Effect of k value on RMSE value in different algorithms

从图3中可以看出，基于用户的协同过滤算法的RMSE值均在1.07附近，而基于项目的协同过滤算法的RMSE值变化较大，均大于0.97，而混合协同过滤方法的RMSE值位于0.95～0.97中间，比两种传统的协同过滤算法均降低了0.1左右.基于混合的协同过滤方法考虑了项目标签属性特征，并且利用基于项目的协同过滤算法计算预测评分并填充用户-项目矩阵，降低了数据的稀疏性，使得不同k值下的RMSE值较小，说明算法预测出的结果具有更好的精确度.因此，在相同的数据条件下，基于混合的协同过滤方法优于两种传统的协同过滤算法.

2) 基于混合的协同过滤方法的灵敏度分析

实验2结果：设置不同的权重因子，比较不同权重因子下混合协同过滤方法的MAE值，实验结果如图4所示.

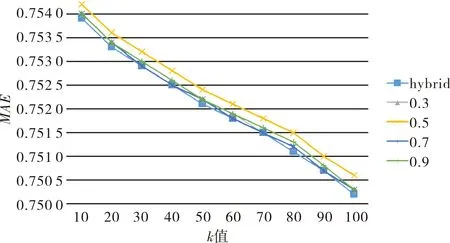
图4 不同权重因子下的MAE值比较Fig.4 Comparison of MAE values for different weighting factors

从图4中可以看出，不同近邻数下(邻居数分别为10、20、30、40、50、60、70、80、90、100)，不同的权重因子计算出的MAE差别较小.当权重因子为0.3、0.5、0.7、0.9时，计算出的MAE值均大于本文方法的MAE值.采用原始权重因子的混合协同过滤方法利用权重因子将项目评分相似度和项目标签属性相似度结合作为项目综合相似度，当用户未对项目进行评分时，项目的最终相似度即为项目的标签属性相似度，并不会出现项目无评分就无法计算项目相似度的情况.由此可见，文中计算所采用的权重因子计算方法较为合理，能够较准确的进行相关推荐.

4 结论

本文在传统协同过滤算法的基础上，提出了一种基于用户-项目混合的协同过滤方法，有效降低了数据稀疏性.同时在利用基于项目的协同过滤算法时引入项目标签属性相似度，综合考虑了除用户对项目评分之外的相关信息，并利用权重因子将项目标签属性相似度和项目评分相似度结合，解决了传统推荐算法存在的推荐范围的问题.因此，本方法在项目数据比较丰富的情况下，能够较为充分的利用项目数据并给出准确推荐.但是本方法主要是离线计算并推荐，在实现有效的实时推荐方面仍需改进，并且方法中仅主要考虑了项目属性，并未充分考虑其他的项目特征.因此下一步工作将尽力优化算法流程，提高算法效率，满足用户个性化信息推荐的需求.