装配式钢混组合梁全息图像拼接方法试验研究

龙 洋， 邵 帅， 周志祥， 邓国军， 黄靖云

(1.重庆交通大学土木工程学院， 重庆 400074； 2.深圳大学土木与交通工程学院， 深圳 518060； 3.省部共建山区桥梁及隧道工程国家重点试验室， 重庆 400074)

装配式钢混组合桥梁采用全装配式施工，具有容易保证质量、施工安全性高及对环境和交通影响小的特点，该施工方法可以有效实现桥梁工程的产业化、信息化和绿色化，已发展为现代组合结构桥梁的主要趋势[1-2]。在装配式钢混组合结构桥梁的后期检测中，桥梁的稳定性是确保其安全正常工作的重要指标。

全息图像作为组合结构桥梁后期检测的一项重要指标，其中主要包含了结构在各工况全息变形时相对应的结构全息轮廓线的信息，一定程度上解决了接触式位移传感器受制于数量有限的问题，而造成的测点之间的试验梁区域挠度信息无法准确获取以及整体线形变化存在较大误差累积的问题，实现了变形曲线真实反映出试验梁在荷载作用下的结构与杆件的变形以及结构整体损伤与区域损伤等全部损伤信息。在实际工程中，存在桥梁体量大摄像视域小的问题，因此采用图像拼接技术实现单幅图包含全桥影像的目的。图像拼接现已发展为一项成熟的图像处理技术。文献[3]率先提出Forstner算法，先定位出图像中的角点，然后基于SIFT算法实现特征匹配，但是此算法不能显著增加匹配特征点的数量。文献[4]提出基于不同图像所截信息熵的基础上，建立图像之间的关系，再根据SIFT算法进行匹配，该算法在一定程度上提高了匹配的时效性，但同时降低了匹配精度。文献[5]提出引入Hu矩阵，提高了图像匹配的精准度。

为此，提出一种基于Harris算子与随机抽样一致(random sample consensus，RANSAC)算法相结合的图像拼接方法，对试验梁各个局部图像进行拼接整合从而获得全梁线形图片，最终实现对桥梁整体的健康检测。

1 钢混组合梁试验

1.1 试验概况

完成3片不同损伤位置及程度的装配式钢混组合梁的制作，以进行基于影像轮廓线叠差分析获取桥梁全息变形的研究。钢混组合试验梁主要构造如图1所示，纵向总长7 160 mm，计算跨径7 000 mm，总高770 mm，钢桁高630 mm。上下弦杆选用Π型截面，钢桁梁节点焊接联结杆件，腹杆选用槽型截面。在试验梁的加载点位置和支座位置设有横向加劲钢板，以防止局部屈曲。试验首先对钢桁-混凝土组合梁的腹杆施加特征损伤，然后完成逐级加载并采集数据，当试验梁接近明显屈服时停止加载。

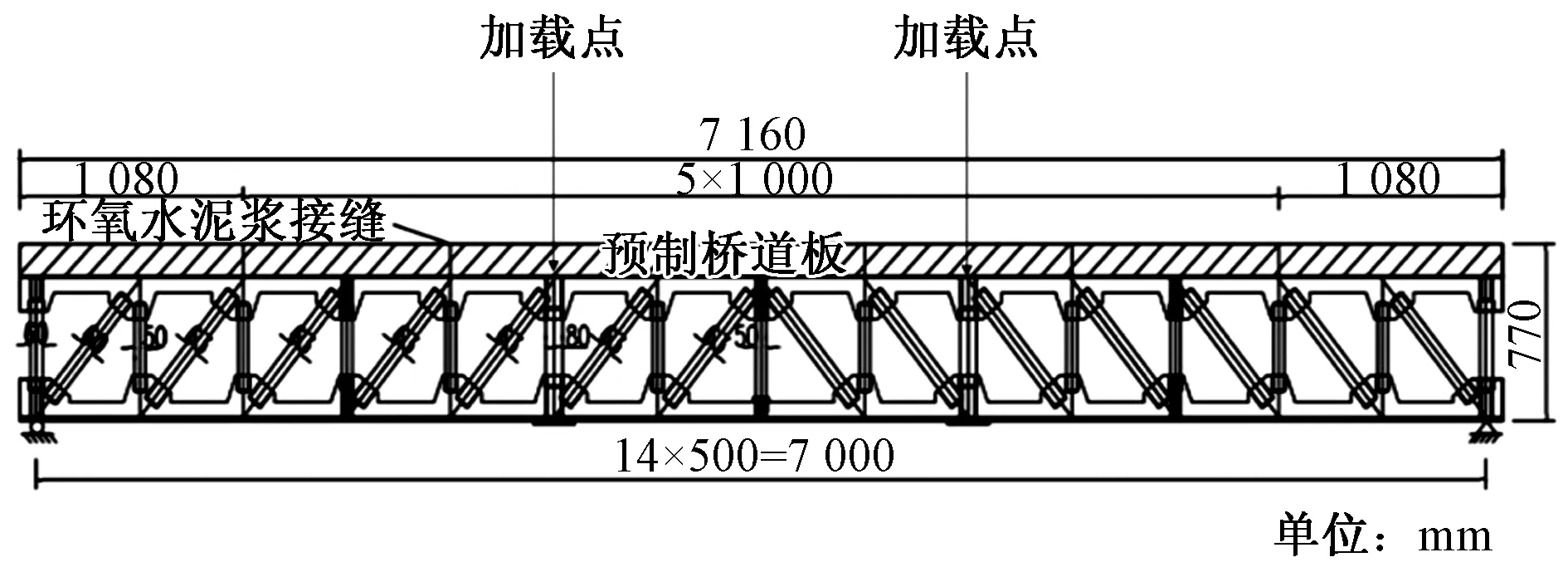
图1 试验梁构造Fig.1 Construction of test beam

首先进行无损伤工况，然后对试验梁施加人工损伤，依次切断钢混组合试验梁的斜杆，模拟实际工程中钢桁杆件损伤失效的情况。试验旨在探究在已知损伤工况和结构外部荷载输入确定情况下的试验梁的力学能力,采用遗传算法及全息位移反映结构状况。

1.2 形态图像数据采集系统

形态图像数据采集系统主要由三个部分组成，分别是可移动轨道车、高清相机和三角支架作业平台。将移动式轨道车当做拍摄设备的载体，并且保持车速稳定，分别在试验梁的两侧设置一个并行轨道，两个轨道设置相同的起始位置。形态图像数据采集系统如图2所示。

图2 形态图像数据采集系统Fig.2 System ofimage data acquisition

1.3 加载及量测

试验钢桁-混凝土组合梁以简支梁作为受力模式，设置反力支座于梁体两端下部，一侧设为铰支座，一侧设为滑动支座。加载系统采用试验室的两个电控液压千斤顶，对试验梁施加两点对称向下荷载，2个加载点分别距两端支座2 500 mm。试验采用分级加载方式对装配式钢混组合试验梁在各损伤工况下的力学性能进行测试。正式试验前，以20 kN为增量由0加载至100 kN后卸载。正式试验分为3个阶段：第一阶段是无损工况加载试验，从0逐级缓缓加载到320 kN，每级荷载的递增量为40 kN，每次加载完成后保持荷载1 min恒定，1 min后进行装配式钢混组合试验梁全息形态图像数据、位移传感器数据及应变片数据的采集；第二阶段是斜杆损伤工况下试验梁加载试验，分3次对称切割试验梁斜杆，每次切割两根，其切割顺序如图3所示，按图3中标注数字1～6的顺序依次进行切割，对这3个损伤工况进行同第一阶段一样的加载与量测工作。

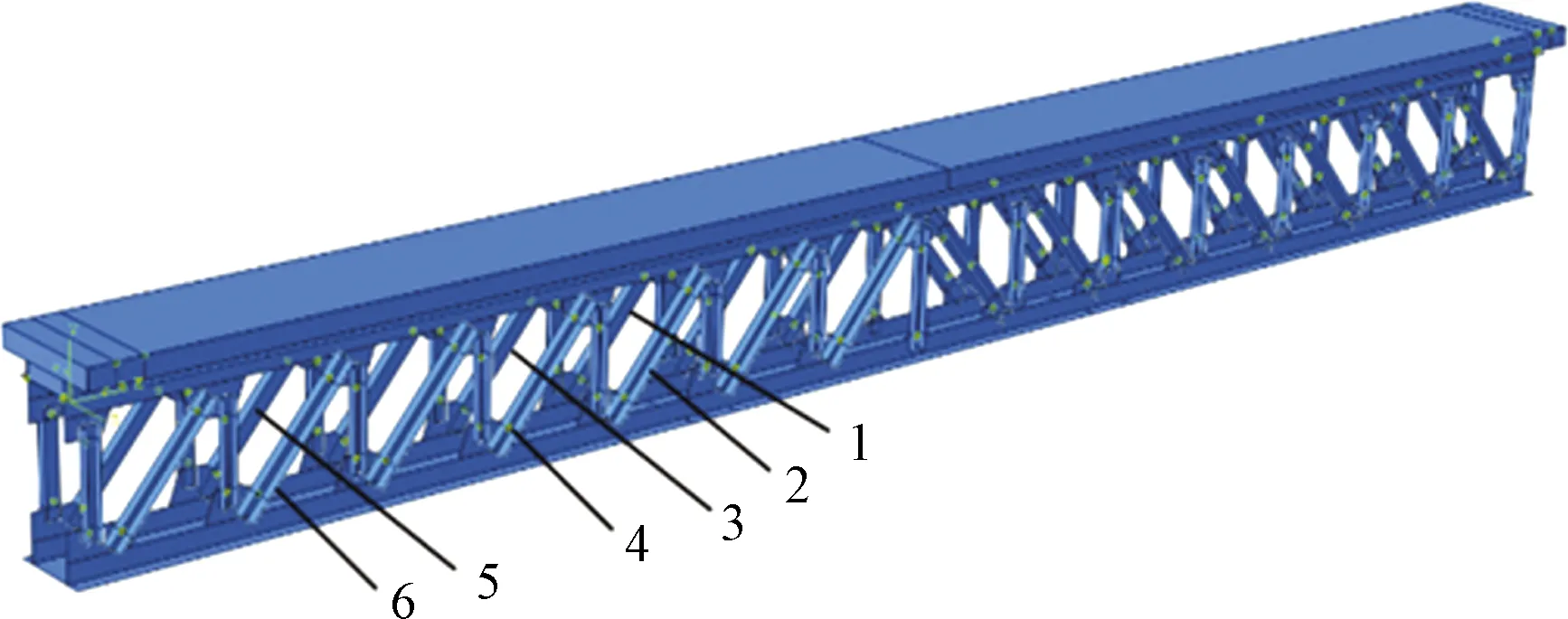
1～6表示所指位置的损伤顺序图3 斜杆损伤顺序Fig.3 Diagonal bar damage sequence

1.4 数据采集及整理

以损伤两根斜杆状态下0～32T工况为例进行说明，即用1T表示10 kN。由位移传感器采集到试验梁各测点的位移如图4所示。

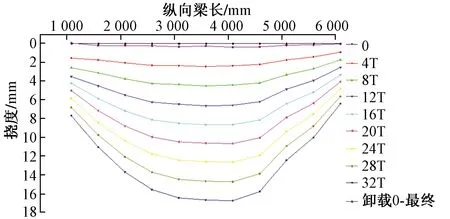
图4 损伤两根斜杆状态下各工况下试验梁位移Fig.4 Experimental beam displacement under two working conditions with two inclined rods damaged

2 全息图像拼接算法

基于全息桥梁图像的轮廓线，能够实现桥梁后期健康检测，由于实际桥梁体量庞大，很难拍摄全息图像，故采用图像拼接方法实现全息图像的获取。

2.1 SIFT算法匹配

尺度不变特征变换(scale invariant feature transform，SIFT)即计算机视觉里检测和表征图像局部特征的一种检测算法[6]。SIFT对图片转动、图片尺度改变、图片中亮度改变具有不变性。SIFT算法具体可以分为3个核心步骤：检测、确定特征点主方向及特征描述的生成。

2.1.1 检测

将高斯函数G(x,y,σ)与输入图像I(x,y)卷积，进而获取图像高斯金字塔(图5)，拉普拉斯函数表达式L(x,y,σ)为

(1)

L(x,y,σ)=G(x,y,σ)⊗I(x,y)

(2)

式(1)中：G(x,y,σ)为高斯核；⊗表示卷积;x,y表示坐标系中的坐标值；σ表示所构建高斯核的方差。

引用高斯差分函数D(x,y,σ)，以便确保检测点的稳定性。其表达式(3)为

D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]⊗

I(x,y)=L(x,y,kσ)-L(x,y,σ)

(3)

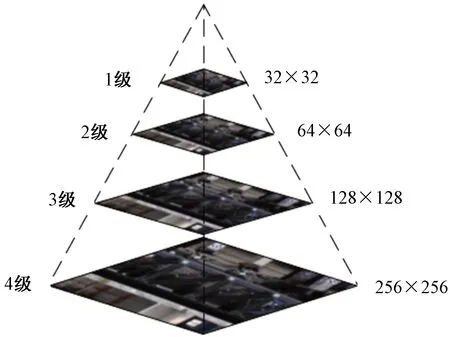
图5 高斯金字塔示意图Fig.5 Schematic diagram of Gaussian pyramid

式(3)中：k为常数；L表示关键点所处的空间。

完成以上步骤可获得图像的尺度空间。为了避免小部分区域极值的出现，在尺度空间中检查极值的过程中，将所有像素点在尺度空间中进行搜索比较，搜索范围为相邻的相同层、相邻的上下两层。结果表明，相邻上层有9个像素点，相邻下层有9个像素点，相同层有8个像素点，一共26个像素点。

2.1.2 确定特征点的主方向

特征领域中像素点的梯度走向决定对应特征点的主方向。数字图像梯度方向表达式为

m(x,y)={[L(x+1,y)-L(x-1,y)]2+

(4)

(5)

式中：m(x,y)表示数字图像梯度绝对值大小；θ(x,y)表示数字图像梯度的角度方向。

选取高于0.8倍最大值的位置拟合，然后确定梯度方向统计图的最大值，确定特征点主方向，如图6所示。

2.1.3 特征描述的生成

根据试验结果，获得8×16=128个特征描述数据，也就可以得到用来表示特征的向量S=[s1,s2,…,s128]T。使用向量S时，需对其完成高斯加权处理，然后根据欧式距离最近原则，将特征点进行匹配。

基于SIFT算法匹配获取全息图片如图7所示，并用红线框选拼接不良部分，可以看出拼接而成的全景图片出现严重缺陷，全景图片效果不能满足课题要求，所以需要对SIFT算法进行改进，以提高拼接质量。

图7 拼接效果不良的全景图片Fig.7 Panorama with poor stitching effect

2.2 基于改进SIFT算法的全息图像拼接

由上述拼接不良的全景图片可知，基于SIFT算法实现的图像拼接存在缺陷，高分辨率钢混组合试验梁照片的局部图像拼接出现了以下现象：图片噪声增加、图片拼接效果很差、像素点丢失和信息缺失。因此，将SIFT算法进行改进，改进后的图片拼接整体步骤流程如图8所示，具体步骤如下。

Step 1取代原来DoG算子，用Harris算子重新描述图像关键特征点。

Step 2在RANSAC算法基础上筛选配对完成的特征点[7]实现再次匹配，并且获取影像变化模型。

Step 3基于加权平滑算法在拼接范围内实现灰度光滑处理，最后获得全景图像。

2.2.1 特征匹配

像素点θ(x,y)的自相关矩阵可以表示为

(6)

式(6)中：M为模值；θ为角度；Ix、Iy为像素点θ的灰度；对x、y各自方向的偏导，Ixy为二阶混合偏导。

Harris特征点响应函数f表示为

f=detM-ktr2M

(7)

式(7)中：detM表示M行列式；k为常数，且k>0；一般取值范围为0.04～0.06；tr为自相关矩阵M的迹。

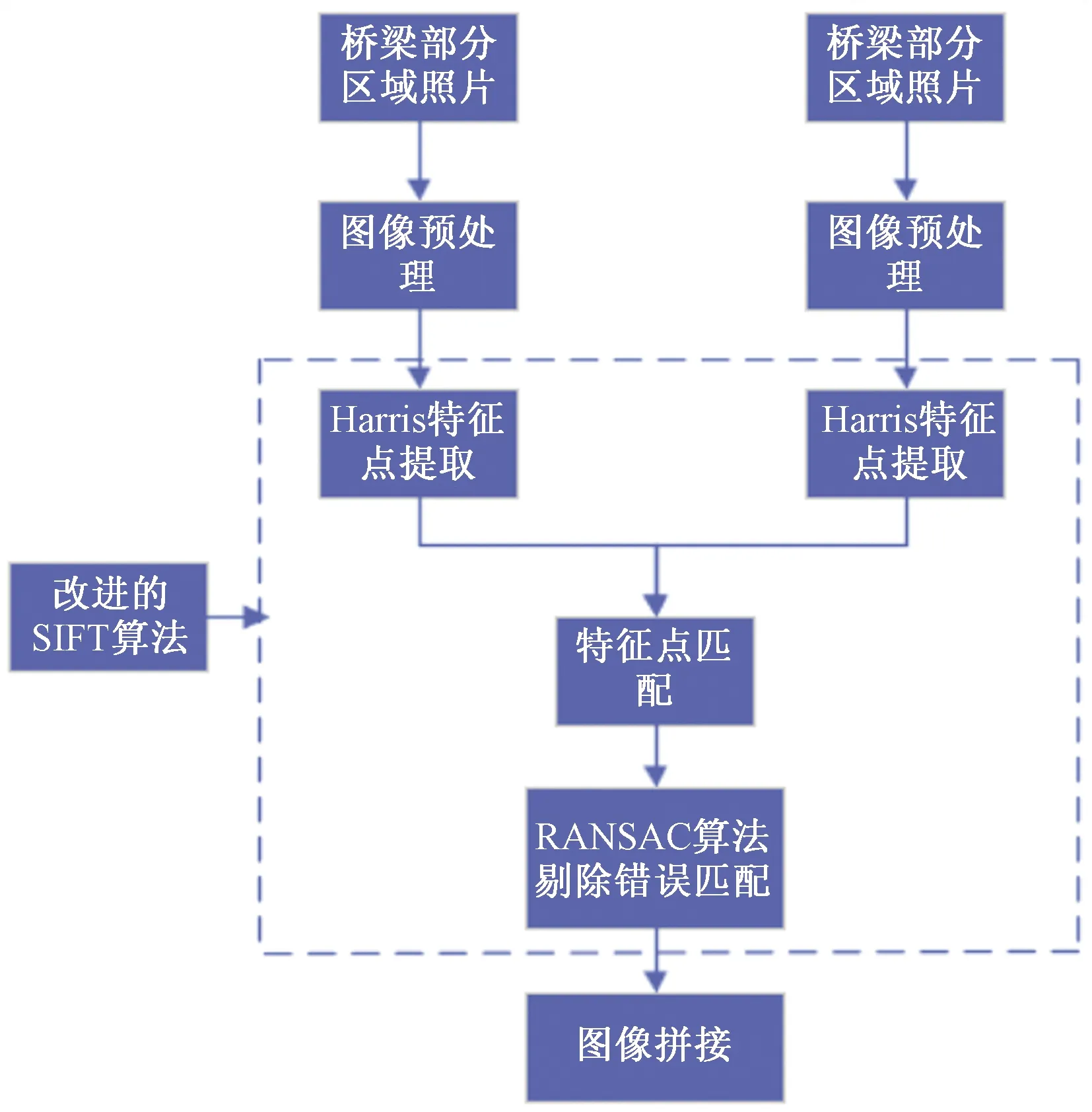
图8 改进算法流程图Fig.8 Improved algorithm flowchart

基于最小欧式距离判别法筛选源照片中相似的特征点，在k-d树搜索算法[8]基础上，获取特征点之间的最小欧式距离点R和次小欧式距离点S，预先设定判定值μ，如果满足条件：β1/β2<μ，则表示特征点相似配对正确，反之特征点β无法筛选到与之匹配的特征点。

(8)

式(8)中，rij和sij为特征向量中的元素。

(9)

(10)

2.2.2 RANSAC算法进一步优化

RANSAC算法是鲁棒性很高的一种变换估计算法[9]，通过去除一些有错误的配对，以提升配准正确率。获取RANSAC算法3个参量。

(1)随机采样的次数。通过预设适当的样本采集数目N，减少配对组合的搜索数量，比较于匹配点而言，尽量让样本数量σ成为域点的概率p大，一般定为95%，取p=0.99，σ=7。设采样点中随机的匹配对是域点的可能性是p′,则不是域点的可能性是q=1-p′，取q=0.4，则次数N为

N=lg(1-p)/lg[1-(1-q)σ]=167

(11)

式(11)中：N表示随机采样次数。

(2)阈值确定。由于钢混组合试验梁的图像很难满足常规的阈值计算公式和变换模型参数公式中的假设条件，于是在钢混组合试验梁图像的基础上，随机抽取7对匹配点并且循环采样167次，最后计算实际坐标与变换坐标之间距离的标准差，经过重复采样计算，以2.45倍的最小标准差作为判断阈值，将筛选出标准差最小的一组配对。

(3)域点数目的确定。采用合适的判定值进行筛选，只要满足两特征点的原坐标与改变后的坐标距离标准差在判定值范围内，则取该匹配对为所需要的匹配；否则判定该匹配对为错误匹配。

2.2.3 特征匹配及优化结果

基于图像数据采集系统，选取4张包含全桥信息且具有重复区域的连续试验梁照片，同时将照片里面存在的重复区域用红色线条框选，如图9所示。

图9 具有重复区域的试验梁连续照片Fig.9 Continuous photo of test beam with repeating area

基于本文方法，对图9进行特征点的筛选、配对和优化，结果如图10所示。

图10 试验梁各局部照片匹配结果Fig.10 Matching results of each part of the testbeam

2.2.4 图像拼接

在透视变换模型的基础上，将匹配后的照片转变到相同坐标系中完成拼接[10]，该模型如式(12)、式(13)所示。

(12)

(13)

然后在加权平均融合方法[11]的基础上，实现接缝处的平顺化，将局部图像g1和g2拼接而得的图像G为

(14)

式(14)中：g1、g2为对应局部图像的权重值，其数值范围是(0,1)，具体数值由局部图像之间重叠区域的大小决定，试验依据局部图像之间重叠部分的大小，取g1=g2=0.5，而表示接缝平顺过渡程度的数值含义即为g1由0到1，g2由1到0的各自的渐变能达到均衡统一。

图像拼接的整体算法流程：①对源图像完成预处理；②用Harris算子替换DoG算子对局部图像进行特征点描述提取[12]，在SIFT算法对特征点配对范围内，通过RANSAC算法实现对特征点的二次筛选[13]，并且去除配对误差；③基于加权平均融合法对拼接区域进行平顺处理，获得钢混试验梁全景图像。

图11 融合图片Fig.11 Fused picture

2.2.5 拼接结果的评价

试验基于Intel core i5-6500 CPU主频为3.2 G和内存为8 G的主机，并且在MATLAB 2018a仿真环境下运行，在改进的SIFT算法基础上，进行桥梁局部图像拼接，如图11所示。与拼接图片相比，容易看出拼接效果大大提高，没有显著拼接缺陷。

关于图像拼接效果的衡量，在图像应用领域中有许多客观指标，均可以用来衡量拼接的质量，采取信息熵作为衡量图像质量的客观参数[14]，表达式为

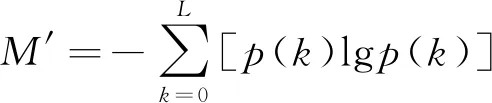
(15)

式(15)中：M′为熵，其数值由大到小表示照片的拼接效果由好到差；p(k)为概率，表示当照片中像素灰度为k时的可能性。

综合上述方法，分别得出拼接后全景图片和定点摄影全景照片的信息熵，对其进行客观评价指标比较，结果如表1所示。

由表1可以发现，基于改进SIFT算法实现的拼接结果良好，并且拼接后图像包含的信息更加丰富，能够满足课题组全息变形测量需求。

表1 图片熵对比Table 1 Comparison of picture entropy

3 试验结果及处理

试验采用装配式钢混组合梁为试验对象，对其进行损伤加载工况的位移测量，并选取损伤两根斜杆状态下0～32T工况为例进行说明。当采用传统的百分表进行测量时，采集结果如图12所示，其中N1～N11表示11个接触式位移测量器所设的位置，对应每条位移曲线上的11个点。

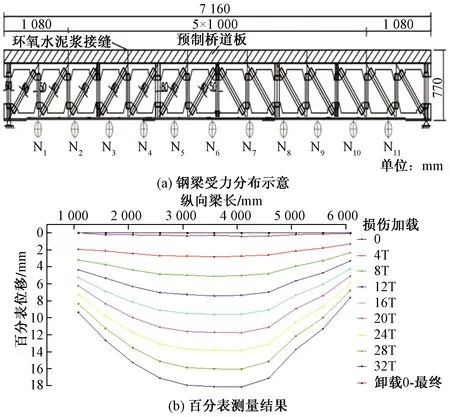
图12 钢梁受力分布及百分表测量结果Fig.12 Results of dial indicator measurement and stress distribution of steel beam

由图12可知，传统测量方法所得结果是分散的，不能反映桥梁的全息变形，因此需采用课题组提出的全息测量方法。基于SIFT算法对图像进行拼接并获取位移曲线结果如图13所示。

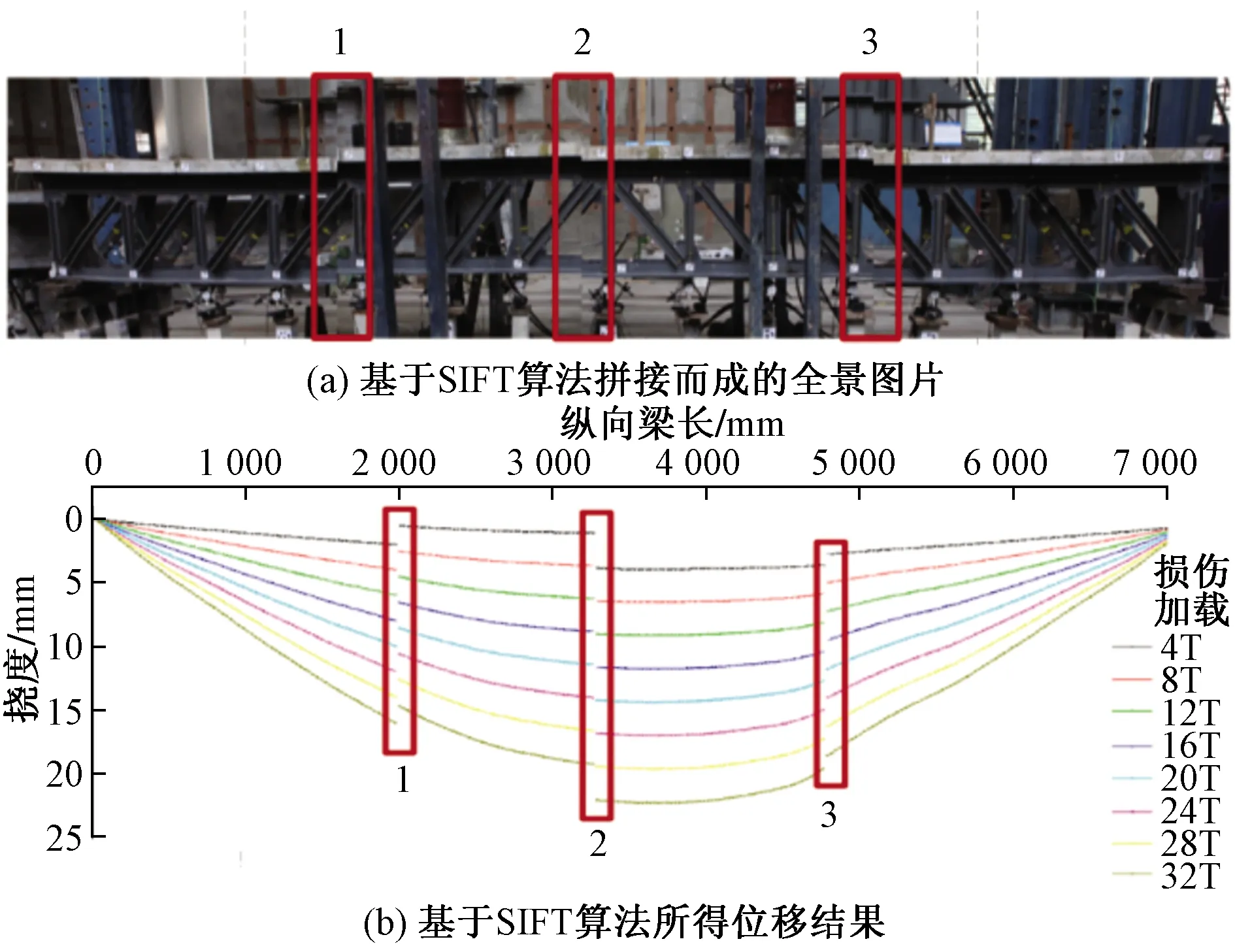
红色框选出的位置代表拼接不良处，分别对应位移 曲线[图13(b)]中的相应位置图13 基于SIFT算法拼接而成的全景图片和所得位移结果Fig.13 Panoramic image mosaic and displacement results based on SIFT algorithm

由图13可知，基于SIFT算法的图像拼接存在拼接不良的现象，导致位移曲线出现跳跃的现象，不能真实反映梁体的全息变形，因此需对SIFT算法进行改进。基于改进的SIFT算法，实现图像的拼接并获取位移曲线，如图14所示。由图14可知，基于改进后SIFT算法获取的试验梁位移结果图中曲线十分光滑，能够较好反映桥梁各点处的位移，符合研究需求。

图14 基于改进后SIFT算法拼接而成的全景图和所得位移结果Fig.14 Panorama stitched displacement results by improved SIFT algorithm

4 结论

基于试验梁的全景图像获得梁体的变形位移曲线是比较平顺饱满的，相比较传统接触式位移测量方法，克服了因传感器数量限制使观测点响应数据离散的问题，能真实、连续地反映结构全局损伤与局部损伤信息，由于是全桥线形的获取，即便曲线是由大量的像素点构成，但此类线形更接近真实的数理线形，实现了精度上的提升，对于以后依据挠度线形的桥梁健康监测有重要意义。