构造“距离”证明不等式的求解策略

蔡旦利

(浙江省诸暨中学，311800)

构造法是一种重要的数学解题方法,它是通过观察,抓住问题的特征,联想熟悉的、简单的和直观的数学问题和数学模型,然后将问题进行转化,恰当地构造新的数学模型来达到解题的目的.本文以“构造距离”证明不等式为例，分类进行探究.

一、一定点到直线上点的距离

例1已知a,b∈R,且a+b+1=0,求证:(a-2)2+(b-3)2≥18.

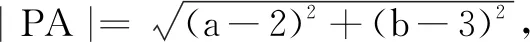
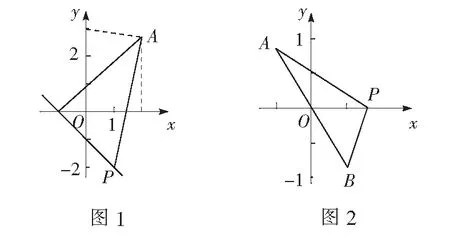
二、 两定点到直线上点的距离之和

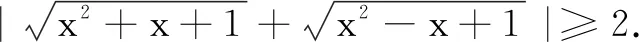
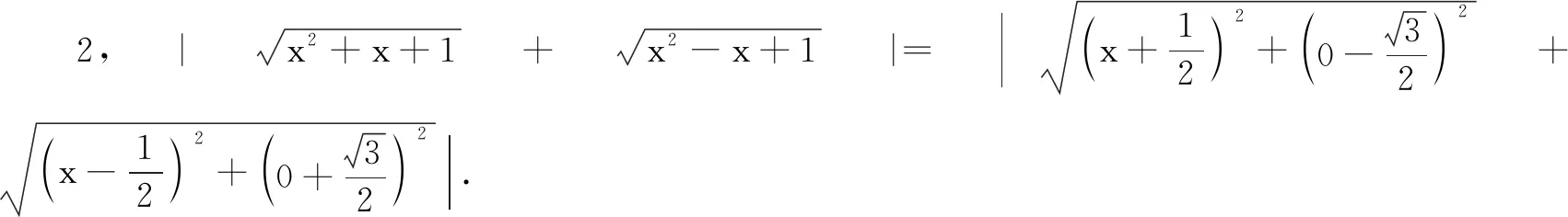
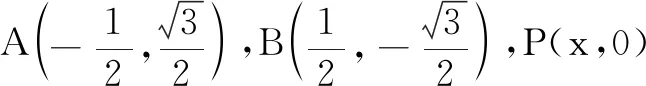
三、一定点到直线和点的距离比较

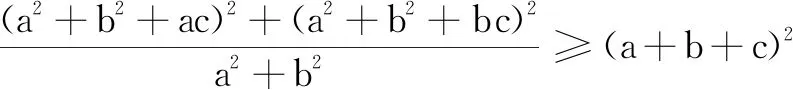
证明现将原不等式两边同除以a2+b2,然后两边开平方，得

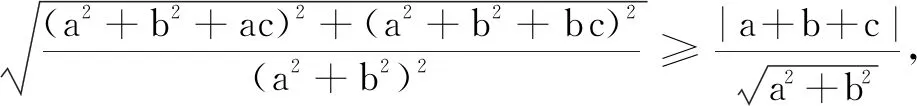
四、构造 一定点到曲线上点的距离

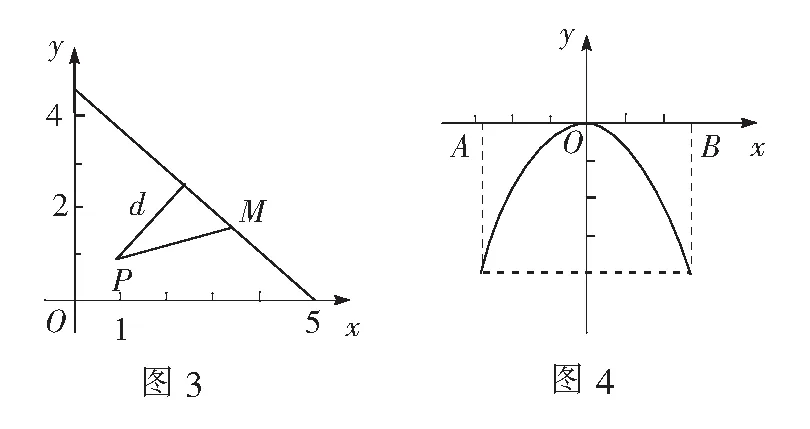
例4求证:对任意θ∈R,恒有(3+2sinθcosθ)2+(sinθ+cosθ)2≥4.

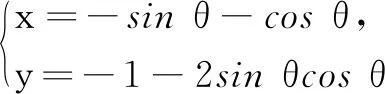
(3+2sinθcosθ)2+(sinθ+cosθ)2=[0-(-sinθ-cosθ)]2+[2-(-1-2sinθ·cosθ)]2可看作是定点(0,2)到曲线y=-x2上点的距离d的平方.如图4，结合图象可得dmin=2,证毕.

五、一定点到区域内点的距离

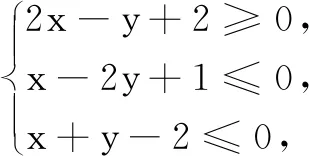
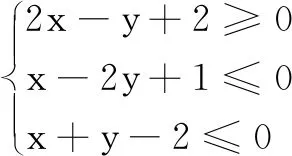
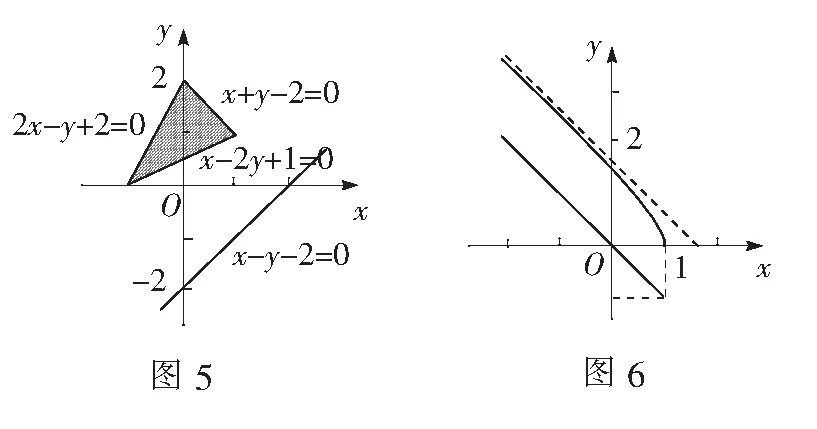
六、直线上的点与曲线间的点之间的距离

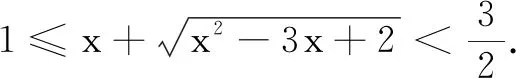
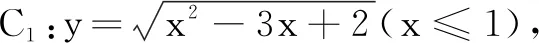
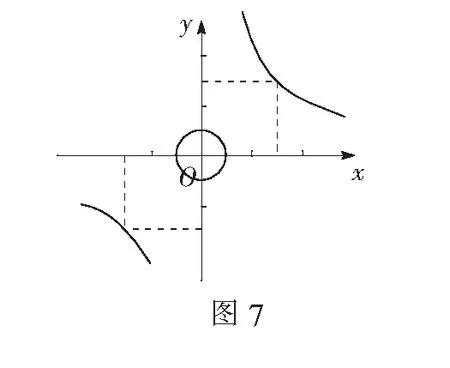
七、曲线间点与点之间的距离

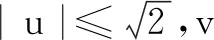
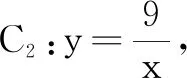
综上可知，构造距离来解决不等式问题,需要足够的知识经验，较强的观察转化能力、综合运用能力和创造能力.解题时应根据题目提供的条件,深入分析问题,找出已知和所证之间的联系,使解题另辟蹊径,水到渠成.构造距离是非常灵活的,不能生搬硬套,但可以尝试寻找不等式的特征.因此，在构造距离解决不等式的过程中,首先得明确构造的目的,即为什么构造;其次弄清问题的特点,以便确定构造的方案.