加权互斥最大集合覆盖问题的精确算法

周晓清，叶安胜，张志强

(1.电子科技大学 计算机科学与工程学院，四川 成都 611731；2.成都大学 信息科学与工程学院，四川 成都 610106)

0 引 言

1 问题及符号的定义

1.1 加权互斥最大集合覆盖问题的定义

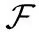
1.2 问题转换

1.3 符号定义

为了描述方便，文中还定义如下符号：

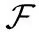
1.4 递归算法时间复杂度的通用公式

假设基于分支搜索方法的递归算法下某个分支后，得到如下的一个递推公式T(n)≤T(n-n1)+T(n-n2)+…+T(n-nr)， 即将原问题分解为r个大小的子问题，其中r≥2，n为原问题的规模(比如图中的顶点数)，ni和n-ni分别为原问题分支后第i个子问题的减少量和第i个子问题规模。令T(n)=xn， 则上述递推公式可以转化为求解方程xn-xn-n1-xn-n2-…-xn-nr=0的最大实根。设c为该方程的最大实根，则在该分支下最坏的时间复杂度为O*(cn)， 称c为该递归关系式的分支因子。由于分支搜索算法不止一个分支，那么就将算法所有分支中最差的运行时间作为整个算法运行时间上界。

2 算法的设计及相关的性质定理

2.1 算法初步思想

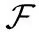
2.2 性质和定理

以下将证明算法设计中用到的一些性质和定理。

证明：假设OPT为实例I中不包含顶点v的最优解，那么存在另外一个可行解OPT′=OPT∪v， 使得 |OPT′∩X|>|OPT∩X| 成立，这与OPT为最优解相矛盾，所以可以将度为0的顶点直接加入解中。

证明：由于交集图G的最大度Δ(G)≤1， 所以交集图G中顶点只存在以下两种情况，要么是度为0的独立点，要么是两个顶点相连的线段。

对于第一种情况，根据性质1可知，可直接将度为0的顶点加入解中。对于第二钟情况，首先判断两个顶点与X相交的情况，将与X相交元素更多的那个顶点加入解，如果两个顶点同X相交元素一样多，那么将权重较小的那个顶点加入解。如此反复操作，即可在多项式时间内解决该问题。

证明：由于交集图G中顶点的最大度Δ(G)≤2， 那么交集图G仅可能是由一条简单的路或者环构成，下面分这两种情况来讨论解决该问题需要的时间。

情况1：假设交集图G是一条简单路。那么首先找到这条路中间的顶点v， 然后从顶点v开始分支，要么将v加入解中(顶点v及其v邻居共3个顶点将从实例I中删除)，要么v不在解中(顶点v从实例I中删除)，所以该分支的递归关系式为T(m)≤T(m-3)+T(m-1)。 经过分支后，交集图G将会分成两个差不多大小的连通分量，有以下递归关系式

解递归关系式得T(m)≤4logm=m2， 所以可在多项式时间内解决。

情况2：假设交集图G是一个环，那么从环中任意选一个顶点v进行分支。同情况1的分析类似，要么将顶点v加入解中，要么顶点v不在解中，因此也有如下递归关系式T(m)≤T(m-3)+T(m-1)。 在该操作后，交集图G成为一条简单路径，所以同情况1 的分析可知，有T(m)≤(m-3)2+(m-1)2<2m2， 所以可在多项式时间内解决。

如果交集图G是由多个简单路和环构成，可以独立求解各个连通分量，然后将所有连通分量求出的解合并起来就为该原问题的解。由于每个连通分量导出的子实例可以在多项式时间内求解，那么原问题可以在多项式时间内解决。

2.3 解决加权互斥最大集合覆盖问题的精确算法

下面是一个求解加权互斥最大集合覆盖问题的精确算法，其主要步骤参见算法1。

输入：加权互斥最大集合覆盖问题的一个实例。

输出：一个最小权重的互斥最大集合覆盖集。

(4)否则如果Δ(G)≤2， 返回多项式时间内求出的较优解。

3 算法运行时间的分析

3.1 传统方法分析算法时间复杂度

其中，m为交集图G中的顶点数。设T(μ) 为搜索树产生的叶子结点数，那么算法中第(3)步的分支操作将产生如下的递归关系式子

T(μ)≤T(μ-(1+d(v)))+T(μ-1)

3.2 测量治之方法分析算法时间复杂度

不同于传统分析方法中将图中的顶点数作为问题的度量，测量治之方法会选择一个更加复杂的度量，这可能会在分析过程中获得一些传统方法所不能得到的算法运行细节，从而可以对给定算法进行更紧致的分析。例如将图中的顶点区分对待，根据图中顶点度的不同对每个顶点赋予不同的权值。可以按如下方式设置赋值方案：

(1)度为0的顶点，权值设为0；

(2)度为1的顶点，权值设为α；

(3)度为2的顶点，权值设为β；

(4)度大于等于3的顶点，权值设为1；

(1)

其中，α和β是满足0<α<β<1的实数，ni表示图中度为i的顶点总数，n≥i表示图中度大于等于i的顶点总数，α和β的值在文章的后面给出。

T(μ)≤T(μ-(1+α×r1+β×r2+r≥3))+
T(μ-(1+α×r1+(β-α)×r2+(1-β)×r3))

(2)

下面根据式(1)中设置的度量，分析该递归关系式的时间复杂度。

情况1.1：当d(v)≤2时，根据定理2可知其时间复杂性为多项时间。

情况1.2：当d(v)=3时，此时算法的时间复杂度根据式(2)分情况计算在表1中。表1计算了交集图G中度为3时的所有可能性，由表1可知在情况1.2下最坏的时间复杂度为O*(1.3172μ)， 又在初始图上μ

表1 情况1.2下递归关系式和时间复杂度

情况1.3：当d(v)=4时，此时算法的时间复杂度根据式(2)分情况计算在表2中，表2计算了交集图G中度为4时的所有可能性，由表2可知在情况1.3下最坏的时间复杂度为O*(1.3247μ)， 同样在初始图上μ

表2 情况1.3下递归关系式和时间复杂度

情况1.4：当d(v)≥5时，此时采用顶点总数为问题规模的传统分析方法有如下递归关系式T(μ)≤T(μ-6)+T(μ-1)， 用1.4小节的方法解得算法的时间复杂度为O*(1.2852m)。

综上4种情况，得到加权互斥最大集合覆盖问题可以在O*(1.3247m) 时间内解决，该结果改进了传统方法分析得到的运行时间界O*(1.3803m)。 其中α=0.5687和β=0.8499是将表1和表2中所有递归关系式作为约束条件组成一个拟凸规划的约束条件，然后对这个拟凸规划求解得到。

3.3 基于测量治之方法改变度量设置进一步改进算法时间复杂度

(3)

其中，α、β和γ满足0<α<β<γ<1的实数，α、β和γ的值在本文的后面给出。

T(μ)≤T(μ-(1+α×r1+β×r2+γ×r3+r≥4))+
T(μ-(1+α×r1+(β-α)×r2+
(γ-β)×r3+(1-γ)×r4))

(4)

下面根据式(3)中设置的度量，分情况来分析该递归关系式的时间复杂度。

情况2.1：当d(v)≤2时，根据定理2可知其时间复杂性为多项时间。

情况2.2：当d(v)=3时，此时算法的时间复杂度根据式(4)分情况计算在表3中。表3计算了交集图G中度为3时的所有可能性，由表3可知在情况2.2下最坏的时间复杂度为O*(1.3131μ)， 又在初始图上μ

表3 情况2.2下递归关系式和时间复杂度

情况2.3：当d(v)=4时，此时算法的时间复杂度根据式(4)分情况计算在表4中，表4计算了交集图G中度为4时的所有可能性，由表4可知在情况2.3下最坏的时间复杂度为O*(1.3132μ)， 同样在初始图上μ

表4 情况2.3下递归关系式和时间复杂度

表4(续)

情况2.4：当d(v)≥5时，此时采用顶点总数为问题规模的传统分析方法有如下递归关系式T(μ)≤T(μ-6)+T(μ-1)， 用1.4小节的方法解得算法的时间复杂度为O*(1.2852m)。

综上4种情况，得到加权互斥最大集合覆盖问题可以在O*(1.3132m) 时间内解决，该结果改进了3.2小节分析的运行时间界O*(1.3247m)。 同样按3.2小节所述的方法求解得到α=0.5148、β=0.7991和γ=0.9785。

4 结束语

本文首先将加权互斥最大集合覆盖问题转化成图上的问题进行处理，然后证明了算法中使用到性质和定理，在此基础上设计了一个分支搜索算法，最后分别采用了两种不同的分析方法分析算法的时间复杂度。第一种方法采用传统方法分析算法时间复杂度，是将图中顶点数作为问题实例的度量，得到算法的时间复杂度为O*(1.3803m)。 第二种方法采用测量治之方法，根据顶点对问题整体难易程度的贡献，对度不同的顶点设置不同的权重，得到了算法时间复杂度为O*(1.3247m)， 在进一步设置更加细致的度量后，得到算法时间复杂度为O*(1.3132m)， 改进了该问题原有的最佳运行时间界O*(1.325m)。