双驱二维工作台的几何误差建模与补偿方法*
2020-12-28王国冰黄江涛张帅华
左 厅,王国冰,李 凯,高 迪,黄江涛,张帅华
(广州汽车集团股份有限公司 汽车工程研究院,广东 广州 511434)
0 引言
为了达到更高的精度和动态性能,双电机驱动技术越来越多地应用在数控装备的进给系统中,其基本概念为驱动力与合外力通过工作台的重心,且没有外部扭转力矩影响[1]。国内外学者多结合现代控制理论,引入各种控制方法如自适应控制、模糊控制[2-4]等来协调两轴间的运动性能,提高其精度。文献[5]利用虚拟轴控制策略,将各从轴的驱动力矩反馈至虚拟轴前向通道中,使得从轴产生的运动变化能够反馈到主轴上。
在众多的误差影响因素中,几何误差是限制机床加工精度的主要因素之一。文献[6]利用压电陶瓷和柔性铰链设计出一种补偿机构,利用软件调整补偿机构的输入电压,从而实现对工作台的误差补偿。文献[7-8]建立了五轴数控机床的误差模型,通过修改NC代码来实现误差补偿,并开发出相应的补偿软件。文献[9]基于误差模型提出了一种修改粗插补代码使运动发生偏移进而实现几何误差补偿的方法。但上述方法的便捷性有待提升,且只能应用于传统的单电机驱动的机床上。本文以双驱二维工作台的几何误差模型为基础,结合BECKHOFF公司TwinCAT自动化控制系统中的电机控制功能,提出了一种虚拟轴-电子凸轮误差补偿方法,能较好地实现双电机驱动进给系统的误差补偿。
1 双驱二维工作台简介
图1为双驱二维工作台结构示意图,以床身坐标系O-XYZ为整个系统的参考坐标系,从下到上分别为床身、沿X向进给的下工作台、沿Y向进给的上工作台,两工作台在其进给方向上都有两组平行且对称布置于工作台两侧的“旋转伺服电机+滚珠丝杠”,在上位机输入相关指令后由控制器、驱动器控制伺服电机,通过滚珠丝杠和螺母将电机输出的角位移转化成工作台在导轨上的直线位移。

图1 双驱二维工作台结构示意图
在双电机驱动进给系统中,工作台的位置同时由两侧的电机+滚珠丝杠运动副的工况和误差所决定,实际情况下两轴之间的机械、伺服特性等难免存在不同,所以工作台两侧的进给量之间也会存在同步误差,工作台中心的进给量x将由两侧共同决定。
2 双驱二维工作台的几何误差建模
按多体理论对双驱二维工作台的各部分进行编号:床身为0;对于下工作台,其中心的进给量由两侧共同决定,所以本文将下工作台分为三个部分,两侧分别为1、2,中心为3,如图2所示,其中,ΔXx1、ΔXx2、ΔXx3分别为下工作台两侧及中心在进给方向上的误差;同理上工作台两侧分别为4、5,中心为6;刀具为7。工作台的拓补结构如图3所示,典型体7实际有多个低序体阵列,但理论上采用不同的低序体阵列进行误差建模不影响其结果,故本文只取其一(0-1-3-4-6-7)进行后续计算。

图2 下工作台进给示意图 图3 工作台的拓补结构 图4 沿X轴平动时6项误差的几何意义
相邻体之间发生相对移动时会分别在6个自由度上各产生一项几何误差。假设一构件沿X方向平动,6项误差元素分别为:定位误差ΔXx、直线度误差ΔYx和ΔZx、偏摆误差θZx、倾斜误差θXx、俯仰误差θYx,如图4所示。类似地,构件沿Y、Z轴方向平动时的几何误差分别为定位误差ΔYy、ΔZz,直线度误差ΔXy、ΔZy、ΔXz、ΔYz,偏摆误差θZy、θZz,倾斜误差θXy、θXz,俯仰误差θYy,θYz。
根据经典的多体系统理论和齐次坐标变换法,忽略高阶无穷小项,下工作台沿X方向进给x时床身0到下工作台1的变换矩阵为:
(1)
(3)

(4)
(5)
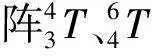
(6)
(7)
由于上工作台6与刀具7并无相对移动,故其齐次变换矩阵视为单位矩。
当理想(无误差)状态下,床身0到刀具7的变换矩阵为:
(8)

(9)
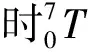
(10)
由于本文的研究对象是只在X、Y方向上进给的二维工作台,无法在Z方向上进给,且在Z方向上所产生的误差较小,因此不考虑补偿Z方向上的误差,以下将θXx、θYx、θXy、θYy、θZx、θZy这些与Z方向位移有关的误差忽略,重点研究ΔXx、ΔYx、ΔXy、ΔYy、θZx、θZy这6项误差。


(11)
从而可得双驱二维工作台的误差模型:
(12)
(13)
式(12)和式(13)表示:当刀具在两方向的理想进给量分别为x、y时,由各项几何误差所引起的刀具在两方向上的定位误差分别为ΔX、ΔY。
3 几何误差测量及补偿策略
图5为虚拟轴-电子凸轮补偿策略原理框图,其实质是一种通过运动控制指令偏置来修正实际输出位置的误差补偿方法。电子凸轮是一种模仿传统机械凸轮的从轴位置关于主轴位置的函数关系,将误差函数以电子凸轮的形式导入运动控制器中,并将凸轮的主、从轴分别与虚拟轴、电机实轴连接,系统将根据虚拟轴的理想位移和电子凸轮表计算出修正后的实轴的位置指令、速度指令,并发送给电机从而实现误差补偿。
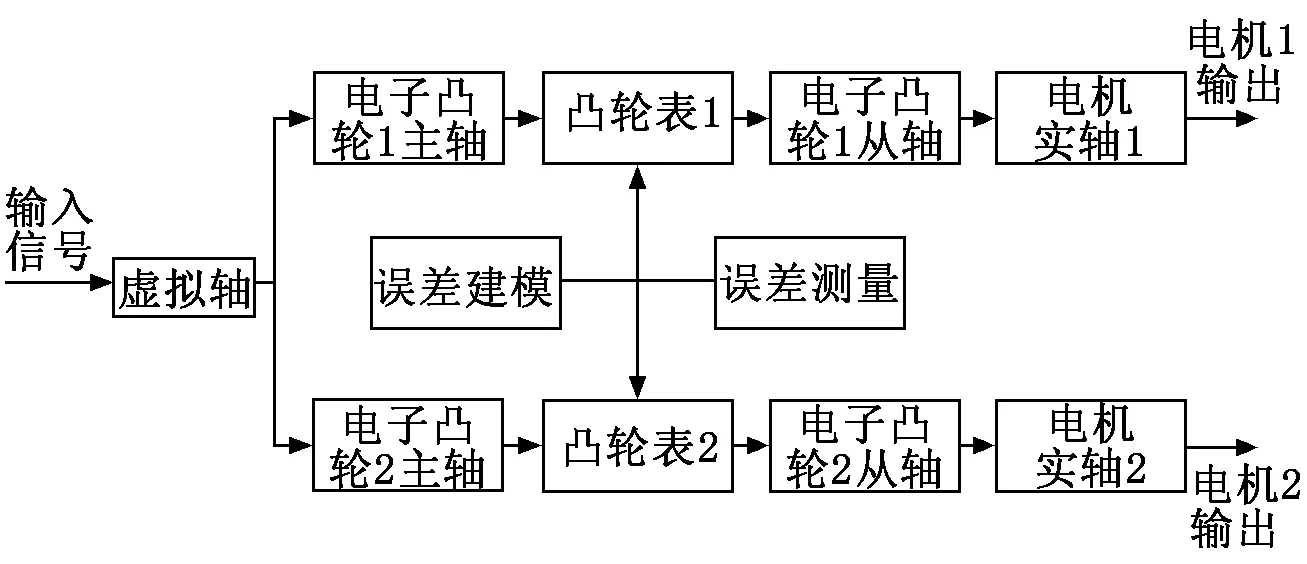
图5 虚拟轴-电子凸轮补偿策略原理框图
设下工作台沿X方向的理想进给量为x,ΔXx是在该方向上的定位误差,则电子凸轮表的从轴位置应该为X=x-ΔXx。当下工作台进给时,只需要给虚拟轴输入指令进给至x处,控制器实际得到的指令是通过电子凸轮修正后的从轴位置X=x-ΔXx,再由控制器、驱动器控制实轴(电机)运动至此处,由于误差ΔXx的存在,实轴的实际进给量Xα为控制器实际指令X与误差ΔXx的叠加,即Xα=X+ΔXx=x,从而达到误差补偿的目的。
假设在电机MX1、MX2、MY1、MY2的同时驱动下工作台沿X、Y方向进给x、y。一般情况下刀具运行的轨迹是已知的,即对于不同的加工工件,x和y存在不同的函数关系y=k(x)。由式(12)可知:刀具在X方向上的误差与定位误差ΔXx1和ΔXx2、直线度误差ΔXy、偏摆误差θZx、进给量y都有关。其中ΔXy和yθZx都是关于变量y的函数,即ΔX是关于(x,y)的二元函数。而电子凸轮是一种凸轮从轴位置关于凸轮主轴位置的一元函数,为了得到电子凸轮的函数表达式以便在误差补偿时应用,可联立刀具轨迹的函数y=k(x)消去y,将ΔX转化为关于x的一元函数。与传统的单电机驱动机床不同,对双电机驱动的工作台误差补偿时,会同时对两侧的电机进行位置修正。假设误差补偿的情况下工作台两侧都按理想位置进给,那么两侧不会产生沿进给方向上的相对位移,根据刚体空间6点定位原理,工作台不会产生绕Z轴的转动,即偏摆误差yθZx为0,进行补偿时不用再考虑。所以各电子凸轮的函数表达式为:
X1=x-ΔXx1-ΔXy.
(14)
X2=x-ΔXx2-ΔXy.
(15)
对于Y方向的误差补偿,其原理与上述相同,则Y方向的各电子凸轮的表达式为:
Y4=y-ΔYy4-ΔYx.
(16)
Y5=y-ΔYy5-ΔYx.
(17)
4 几何误差的测量
误差检测是获取机床几何误差并开展误差补偿的基础,本文利用激光干涉仪作为误差测量工具,在工作台的行程范围内选取120 mm×120 mm的检测空间,除第一个起始点作为参考零位,每个方向上均以10 mm为间隔设置检测点,总计12个。控制工作台单方向进给,采用相对应的光学镜组分别按图6~图8中的测量轨迹对误差补偿所需的各项误差ΔXx1、ΔXx2、ΔYy4、ΔYy5、ΔYx、ΔXy进行检测。为减小检测过程的误差,每项误差检测3次,并取其平均值为结果,如表1所示。
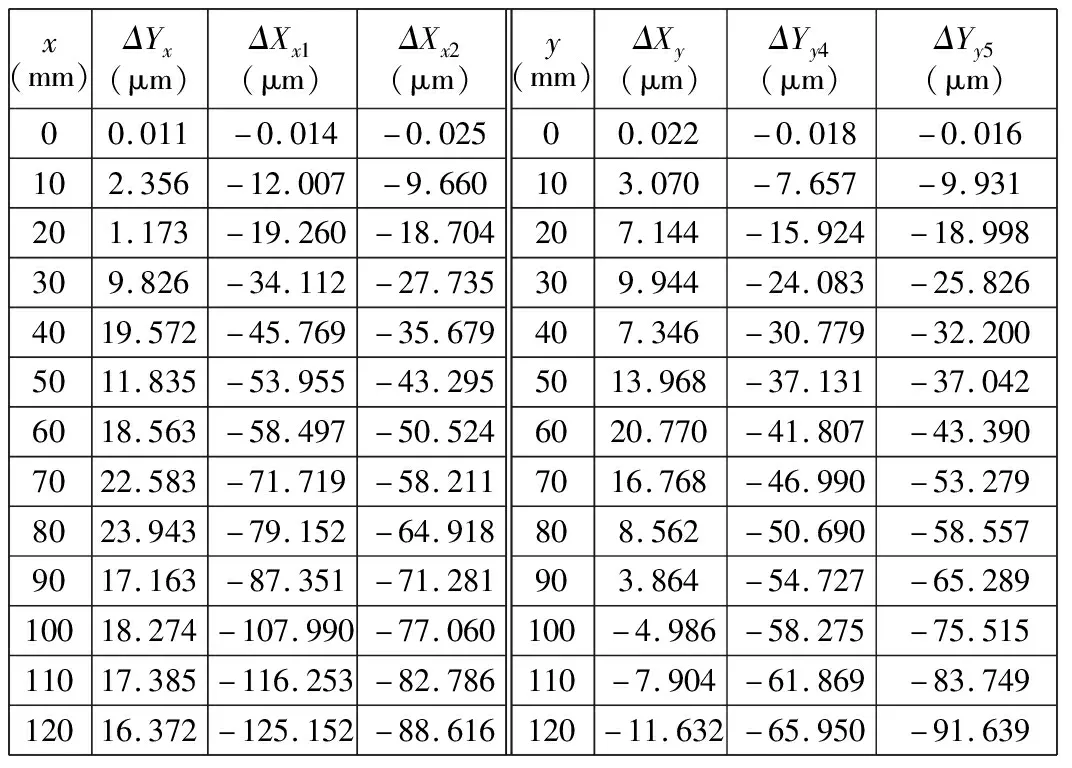
表1 各项误差的测量结果

图6 ΔXx1、ΔXx2的检测示意图 图7 ΔYy4、ΔYy5的检测示意图 图8 直线度误差ΔYx、ΔXy的检测
为得到误差关于进给量的函数,以应用在后续的误差补偿实验中,本文采用最小二乘法对各项误差数据进行拟合,保证拟合确定系数较大的前提下取较简单的拟合函数,分别见式(18)~式(23):
ΔXx1=-0.714-1.028x.
(18)
ΔXx2=-4.347-0.733x.
(19)
ΔYy4=-5.915 3-0.537y.
(20)
ΔYy5=-1.882 5-0.732y.
(21)
ΔYx=-2.826 3+0.551 8x-0.003 3x2.
(22)
ΔXy=1.424-0.227 8y+0.027 9y2-0.000 4y3+1.803×10-6y4.
(23)
5 误差补偿实验
下面利用基于BECKHOFF的TwinCAT控制系统开发的误差补偿软件,对双驱二维工作台开展误差补偿实验,以验证误差模型及补偿方法的有效性。
X、Y方向联动时,设轨迹为y=k(x)=x,联立式(14)~式(23)可得电子凸轮函数表达式,将其导入如图9所示的误差补偿软件中,并分别连接虚拟轴及两实轴进行误差补偿。以10 mm为间隔,通过安装在两侧的光栅尺分别读取两侧定位误差,再根据ΔXx3=(ΔXx2+ΔXx1)/2、ΔYy6=(ΔYy4+ΔYy5)/2可求得工作台中心处的ΔXx3、ΔYy6。检测三次取其平均值为结果,见表2,误差补偿前、后的ΔXx3、ΔYy6对比如图10所示。
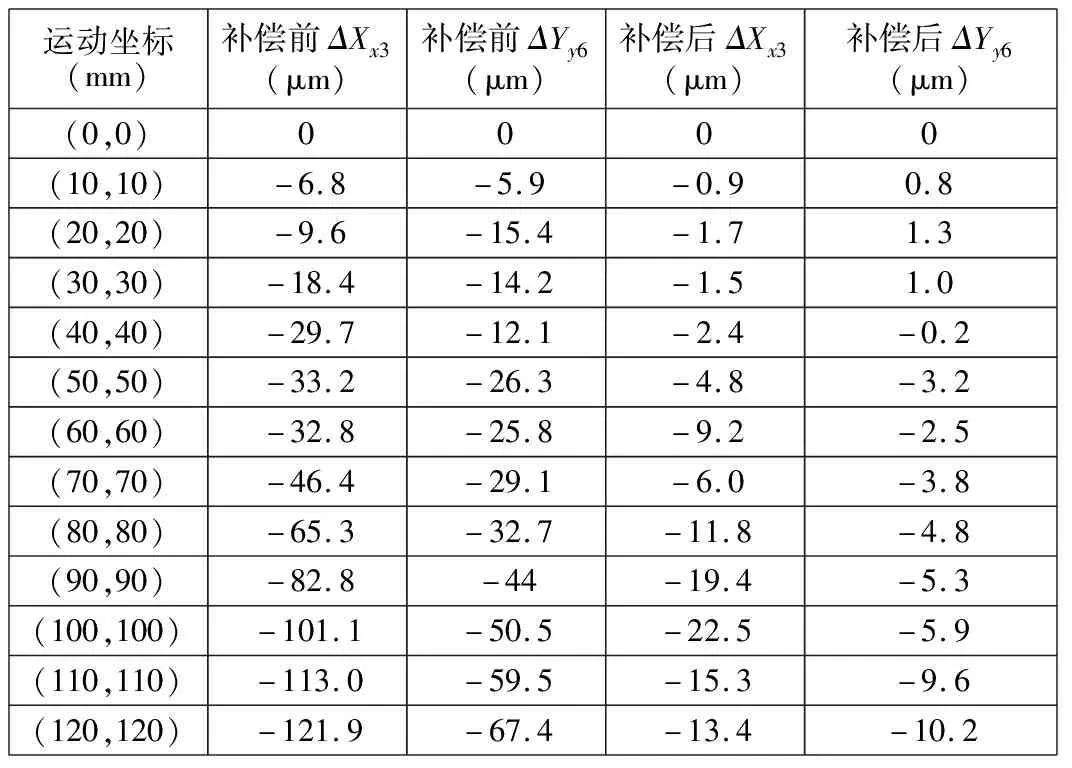
表2 误差补偿前、后ΔXx3和ΔYy6的检测结果
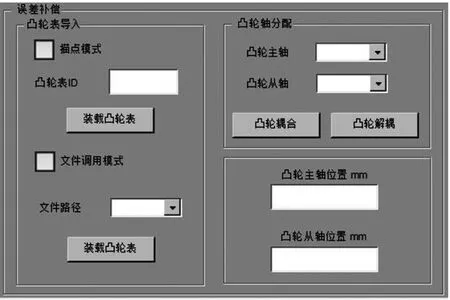
图9 误差补偿软件模块
由图10可以看出:误差补偿前定位误差ΔXx3、ΔYy6总体趋势随行程的增大而增大,且波动较明显;误差补偿后ΔXx3、ΔYy6显著减小,ΔYy6在行程前段保持较小数值,ΔYy6在行程后段小幅增大,且较平稳,最大值为10.2 μm,ΔXx3同样在前段保持较小,在行程后段波动变大,最大值为22.5 μm。总体来看,补偿后的ΔXx3、ΔYy6较补偿前的减小了约70%,效果较为明显。

图10 误差补偿前、后的ΔXx3和ΔYy6
6 结语
针对一种双电机同步驱动的二维工作台进行了几何误差的分析与建模,得到了几项影响较大的几何误差与最终定位误差的函数表达式,为双电机驱动机床的几何误差建模提供了参考。提出了一种适用于双驱二维工作台的虚拟轴-电子凸轮误差补偿方法,并根据误差模型得出电子凸轮函数,导入到基于倍福控制系统开发的补偿软件中,进行了双驱二维工作台误差补偿实验,结果显示补偿后误差减小70%以上,验证了几何误差模型及误差补偿方法较为准确、有效。
