基于改进粒子群算法的风—水—火电力系统短期优化调度
2020-12-28张彬桥
周 瑜,张彬桥,2
(1.三峡大学 电气与新能源学院,湖北宜昌 443002;2.梯级水电站运行与控制湖北省重点实验室,湖北宜昌 443002)
引言
随着全球能源危机的不断加剧和环境污染问题的日益恶化,风电等可再生清洁能源得到迅速发展。风电大规模接入电网,有利于节能减排和提升经济效益。近年来,众多学者对含风力发电场的电力系统优化调度做了详细研究,文献[1]在含有风力发电场的电力系统动态经济调度的模型中,为了解决风电功率的随机波动性和难以预测性,提出了动态经济调度旋转备用的新要求。文献[2]建立在风力发电场预测出力的可信度及风力发电场极限穿透功率的基础上,解决了风电并网的调度问题。文献[3-5]通过研究风电场的电力系统动态经济调度,利用备用容量解决风电的任意波动,从而确保系统的安全性,但牺牲了运行的经济性。文献[6,7]对风速预测方法的改进,提高了风电场电力系统动态经济调度,但没考虑机组的环境效益。文献[8]通过风电全额上网,水电与火电协调分配上网,以减少煤耗量和火电机组出力的总波动量。
本研究将风电引入水、火电力系统中,提出风—水—火电力系统短期多目标智能优化调度策略,以增大风电的输出功率,减小火电的煤耗量,从而减少综合总成本[9-13]。
1 风—水—火电力系统短期多目标优化调度模型
1.1 目标函数
为确保风电的最大输出功率,使风—水—火电力系统运行成本最小,建立如式(1)和(2)所示的目标函数:
式中,E1为系统总费用;t为时段编号;T为调度期的时段总数;Ns为火电厂的个数;为第i个火电厂在k时段的费用;为考虑了阀点效应的第i个火电厂在k时段的出力。
式中,E2为风—水—火电力系统运行的总成本;λk为时段k的压缩因子;为第i个火电厂在k时段的废气排放。
1.2 约束条件
(1)系统发电量平衡约束:
式中,Pt为t时段的负荷(kW·h);P1t为风电厂在t时段的发电量(kW·h);P2t为水电站在t时段的发电量(kW·h);P3t为火电厂在t时段的发电量(kW·h)。
(2)风电场输出功率约束:
式中,Pwk为风电机组k的输出功率(kW);Pwk,min、Pwk,max分别为风电机组k所允许的最小、最大输出功率(kW)。
(3)水电发电流量约束:
式中,QHjt为水电站j在t时段的发电流量;QHjt,min、QHjt,max分别为水电站j在t时段的最小、最大发电流量;Nh为梯级水电站的数量。
(4)水电站库容约束:
式中:VHjt为水电站j在t时段的库容量;VHjt,min、VHjt,max分别为水电站j在t时段的最小、最大库容量。
(5)水电发电功率约束:
式中:PHjt为水电站j在t时段的输出功率(kW);PHjt,min、PHjt,max分别为水电站j在t时段的最小、最大输出功率(kW)。
(6)水量平衡约束:
式中:qHjt为第j个水电站在t时段的天然来水量(m3/s);Mt为第t时段的小时数(h);取初始流量QHj0=0,初始库容为上级水电站在t-τj的时段的出库流量。
(7)水库边界约束:
(8)水电转换关系:
式中:c1,c2,c3,c4,c5,c6为水电站出力—库容—流量系数;j=1,2,3,…,Nh;t=1,2,3,…,T。
(9)火电输出功率约束:
式中:PGit为火电厂i在t时段的输出功率(kW);PGit,min,PGit,max分别为火电厂i的t时段的输出功率的最小、最大值(kW);Ng为系统中火电厂的总数量。
2 基于改进粒子群的模型求解方法
2.1 多目标函数转化为单目标函数
采用线性加权法,将多目标问题转化成单目标问题:
式中:λi为权重系数,它由各个分目标对整个问题的重要程度确定,并确保各目标在数量级上一致,根据多次实际数据运算得到。
2.2 构造惩罚函数
式中:P为所有约束条件;gi(x)为所有约束条件的总称,且gi(x)≥0(i=1,2,3,…,m);z2为所构造的惩罚项。
式中:z为含约束条件的多目标函数。
2.3 基本粒子群算法
粒子群优化(PSO)算法是在模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的优化算法。PSO算法首先随机产生一些粒子,初始化其位置xi和飞行速度vi,在迭代过程中通过跟踪个体极值pbest和全局极值gbest来更新自己的位置和速度。个体极值pbest为粒子自己找到的最优解,全局极值gbest为整个种群找到的最优解[11]。
2.4 引入压缩因子的改进粒子群算法
为了克服传统粒子群算法迭代过程中易出现局部最优而陷入早熟停滞的现象,引入压缩因子到传统粒子群算法,改进后的CFPSO可有效搜索目标空间不同区域,以更快的收敛速度获得最优解。
引入CFPSO的速度、位置更新公式如(15)、(16)、(17)所示。
其中:λ为压缩因子。
3 风—水—火电力系统短期多目标智能优化调度改进粒子群算法的实现
3.1 编码与越限处理
采用实数编码方式对每个粒子的位置向量进行编码,位置向量即表示各个发电机组的输出功率和时间序列。例如编码数1-24用来表示火电机组在24 h以内的输出功率情况,以此类推。由于CFPSO算法在迭代过程中,可能会遇到粒子的速度和位置超过边界条件的情况,处理办法是随机产生相同大小的粒子种群来代替这些越界粒子。生成新粒子种群的位置和速度公式如(18)、(19)所示。
3.2 算法流程
(1)初始种群数50;各时段风—水—火电力系统发电量的位置变量为x,且位置序号为x11,x12,x13,…,x1T,x21,…,x2T,xn1,…,xnT,其中风电发电量为x11~x1T,水电发电量为x21~x2T;火电发电量为xi1~xiT;各时段风、水、火电发电量变化速度为v,且速度序号为v11,v12,v13,…,v1T,v21,…,v2T,…,vn1,…,vnT,其中风电发电量的变化量为v11~v1T,水电发电量的变化量为v21~v2T,火电发电量的变化量为vi1~viT;
(2)将目标函数与约束条件代入惩罚函数;
(3)由多目标函数转化为单目标函数;
(4)求出每个粒子的惩罚函数值,找出所有粒子中的每个粒子的最优值保存在pid,并将所有粒子的最优值保存在pgd中;
(5)求出的最优值是否都满足迭代,如果满足,则计算终止,输出结果;如果不满足,按照压缩因子粒子群算法的更新公式,将其转到第3步继续迭代,直到满足迭代条件,则迭代终止,输出结果。
4 算例分析
采用由风电场、梯级水电站、火电厂构成的典型电网系统进行仿真算例求解分析。该算例模型中包含有:8台风电机组,4台水电机组,10台火电机组组成的风—水—火电力系统,并以系统24 h负载变化为依据进行算例分析。以24 h为调度周期,1 h为1个调度时段,共24个时段,并用Matlab进行编程实现。
所用CFPSO中最大迭代次数为T=200,学习因子c1=c2=1.5,λ=0.6,位置最大值为Xmax=1,位置最小值为Xmin=-1,速度最大值为Vmax=1,速度最小值为Vmin=-1。PSO参数为:c1=1.5,c2=1.5,惯性因子ωmax=0.8,ωmin=0.1。而所对比的基本PSO参数相同,种群规模均取50,迭代次数均取200进行求解,所得的迭代曲线如图1所示。
表1为CFPSO与PSO最终结果对比。通过图1和表1可以看出,CFPSO迭代到第17代就基本趋于稳定收敛,最终得到的综合经济总成本为171 337.9元;而基本PSO迭代到第79代才趋于稳定,最终得到的综合总成本为1 733 799.5元。计算机结果证明了CFPSO算法在求解风—水—火电联合优化调度问题中具有更优的可行性与先进性。
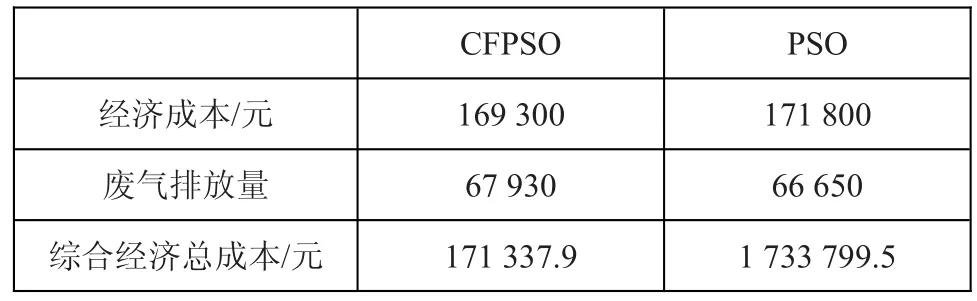
表1 CFPSO与PSO最终结果对比
5 结论
通过典型算例仿真验证了所提出模型和求解方法的有效性,为解决风—水—火电力系统短期多目标智能优化调度问题提供了新的途径。
