空间非合作目标多指包络抓捕路径设计
2020-12-28万文娅孙冲袁建平
万文娅,孙冲,袁建平
西北工业大学 航天学院,西安 710072
空间非合作目标主要包括太空中残留的火箭末级、失效卫星、航天器任务抛弃物、航天器解体及碰撞衍生物等[1]。通常,这类目标的几何外形复杂多样且不具有专门的抓捕对接口,惯性参数和运动参数等信息存在不确定性甚至是未知的,运动规律也较为复杂。空间非合作目标的这些特性造成了在抓捕过程中,抓捕机构和抓捕对象之间存在高动态相对运动,使得难以确定固定抓捕点,因此空间非合作目标在轨抓捕难度很大[2-3]。
针对空间非合作目标抓捕,已经进行了大量的研究,提出了诸如机械臂固定点抓捕、绳系机器人抓捕、柔性机构抓捕之类的方法[4]。本文借鉴多指包络抓捕的思想,利用多指机构在目标物体周围形成一个“包围圈”,以限制目标物体的运动[5]。采用这种方式对空间非合作目标进行抓捕,不仅对空间非合作目标的几何外形具有更好的适应性,还可以提升抓捕的鲁棒性。相比于传统的抓捕方法[6-7],这种方式不需要考虑接触等力学特性,放松了抓捕中对控制的要求。
基于包络的思想,孙冲等提出了一种具有鲁棒性的外包络抓捕方法及抓捕路径优化方案[8]。韩亮亮等提出了一种基于仿章鱼充气软体机器人的碎片捕获装置[9]。然而,由于多指机构自身高自由度的问题以及目标的动态性问题,使得多指机构的包络算法设计还存在诸多难题[5]。
包络问题是由Kuperberg率先提出的,他将包络问题描述为寻找包络点的构型使得多边形目标物体不能任意远离其初始位置[10]。随后,Rimon和Blake将“包络”概念引入到机器人领域,并提出了光滑平面物体的两指包络算法[11]。从此,包络问题成为机器人领域的一个热门研究,相继提出了针对平面目标物体的两指/三指包络算法。两指包络是最简单的包络形式,其适用于凹目标抓捕[12-13]。然而针对凸目标物体,两指机构无法提供封闭的包络构型。由于存在冗余自由度,三指机构可用于包络凸目标,但是其包络构型设计相较于双指机构更为复杂,相关研究人员通常固定某些自由度来简化三指包络问题[14-15]。由于手指数量增加会导致计算量增加,超过三指的多指包络鲜有研究[5]。但是,对于复杂外形的平面物体以及空间物体,则需要更多数量的手指[16]。
在上述研究中[10-16],目标物体都是静态的,而空间非合作目标通常是动态的,目前关于动态物体包络的研究较少。在已有的文献中,Wang等[17-18]和Wan等[19]研究了多机器人对运动目标的包络。与此类似,文献[20-21]研究了多个机器人对动态物体的追捕问题。但是,多指机构不同于多机器人群体,它的各个手指不是独立的,受到多指机构的结构约束。因此,需要设计符合多指机构自身特性的动态物体包络算法。
针对上述提到的多指包络中需要解决的问题,本文提出了一种适用于空间非合作目标的 “主-从”式多指包络算法,不仅具有处理运动目标的能力,而且在包络构型搜索过程中还简化了系统自由度进而提升了计算效率,可以快速地搜索到一条有效的空间非合作目标多指包络抓捕路径。
1 问题描述
针对空间非合作目标的多指包络抓捕问题,本文旨在设计一种“主-从”式包络算法,在给定初始相对构型的条件下,寻找能够约束住空间非合作目标的有效包络构型。
1.1 多指机构结构模型
如图1所示,多指机构由手掌和n个手指组成。其中,每个手指由m个连杆和旋转关节组成。受诸如手掌尺寸和关节允许转动范围等结构约束,多指机构的各个手指间存在内在约束,作为一个整体工作。
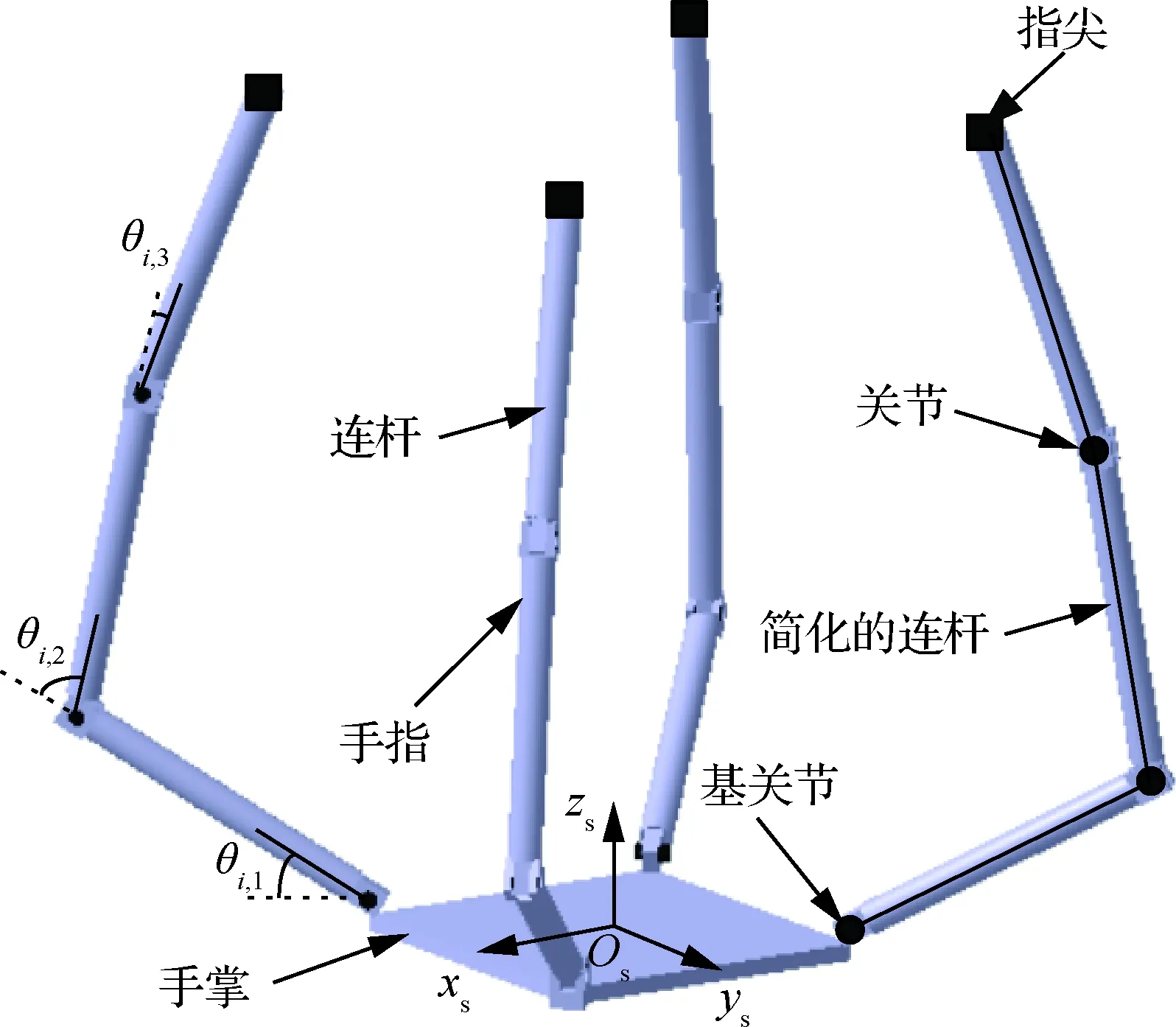
图1 多指机构示意图Fig.1 Multi-fingered mechanism
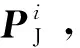
(1)

其次,对于第i个手指的具体构型Ci,它是由自身的关节角θi=[θi,1,θi,2,…,θi,m]T决定的:
Ci=f(θi)=f(θi,1,θi,2,…,θi,m)
i=1,2,…,n
(2)

1.2 空间非合作目标包络条件
本文中空间非合作目标包络条件是指多指机构能够将空间非合作目标约束到某一范围内时,多指机构和空间非合作目标之间应当满足的约束条件。多指机构有效包络住空间非合作目标意味着空间非合作目标不能从多指机构的约束中逃离。具体来说,就是不能从多指机构相邻手指的间隙以及各个手指的指尖间隙中逃离。不失一般性,将多指机构的各个手指的连杆和关节分别简化为线段和点(图1中的黑色线段和圆点)。

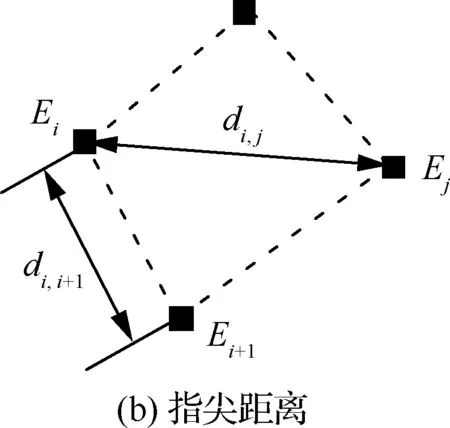
图2 空间非合作目标包络条件推导示意图Fig.2 Derivation of caging conditions for space non-cooperative target
首先,计算第i个手指和第(i+1)个手指连杆间的间隙。如图2(a)所示,由第i个手指和第i+1 个手指的第k个连杆组成的图形为空间四边形Ji,kJi,k+1Ji+1,k+1Ji+1,k(i=1,2,…,n;k=1,2,…,m;Ji,m+1=Ji,e,Ji,e表示指尖)。需要指出,当i=n时,Jn,kJn,k+1Jn+1,k=Jn,kJn,k+1J1,k+1J1,k,手指相邻。如果Ji,kJi,k+1Ji+1,k+1Ji+1,k对边间的距离小于目标相应的特征长度lcl,那么目标则不能从第i个手指和第(i+1)个手指的间隙中逃离:
i=1,2,…,n;k=1,2,…,m-1
(3)
式中:di→i+1,k表示线段Ji,kJi,k+1和线段Ji+1,kJi+1,k+1之间的距离;di,k→k+1表示线段Ji,kJi+1,k和线段Ji,k+1Ji+1,k+1之间的距离。
接着,计算各个手指的指尖之间的距离。如图2(b)所示,多指机构的各个手指的指尖形成了一个空间n边形,第i个手指的指尖Ji,e和第j个手指的指尖Jj,e(i,j=1,2,…,n;i≠j)之间的距离di,j为
i,j=1,2,…,n;i≠j
(4)
式中:d(·,·)表示空间中任意两点间距离计算的函数,本文中采用欧几里得距离,此时p=2。为了保证目标不从指尖的间隙中逃离,应当满足如下关系:
(5)
进一步地,结合方程(3)和(5),运动物体包络条件可以表示为
g(Θ):=max(di,i→i+1,di,k→k+1,{di,j})-lcl<0
(6)
式中:i,j=1,2,…,n(i≠j);n+1=1;k=1,2,…,m-1。
注1特别地,当包络问题可以简化为二维平面包络时(空间非合作目标为扁平型),多指机构的各个手指可以简化为点手指,即用指尖表示。此时,多指机构可以用一系列存在位置约束的点表示(例如图1中的指尖)。进一步,包络条件可以只用方程(5)来描述。
2 “主-从”式包络算法设计
为解决多指机构对空间非合作目标实施包络抓捕时存在的多指机构高自由度以及待包络物体具有动态性的问题,本文提出了一种“主—从”式包络算法。总体思想是:将多指机构的手指划分为一根主手指和其余从手指,并控制主手指的基关节与包络点之间的运动同步,接着调整主手指的关节角使得主手指的构型与包络边尽可能地匹配,然后根据多指机构的结构模型确定其余从手指的构型,最后根据包络条件选择能够约束住空间非合作目标运动的有效包络构型。
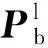
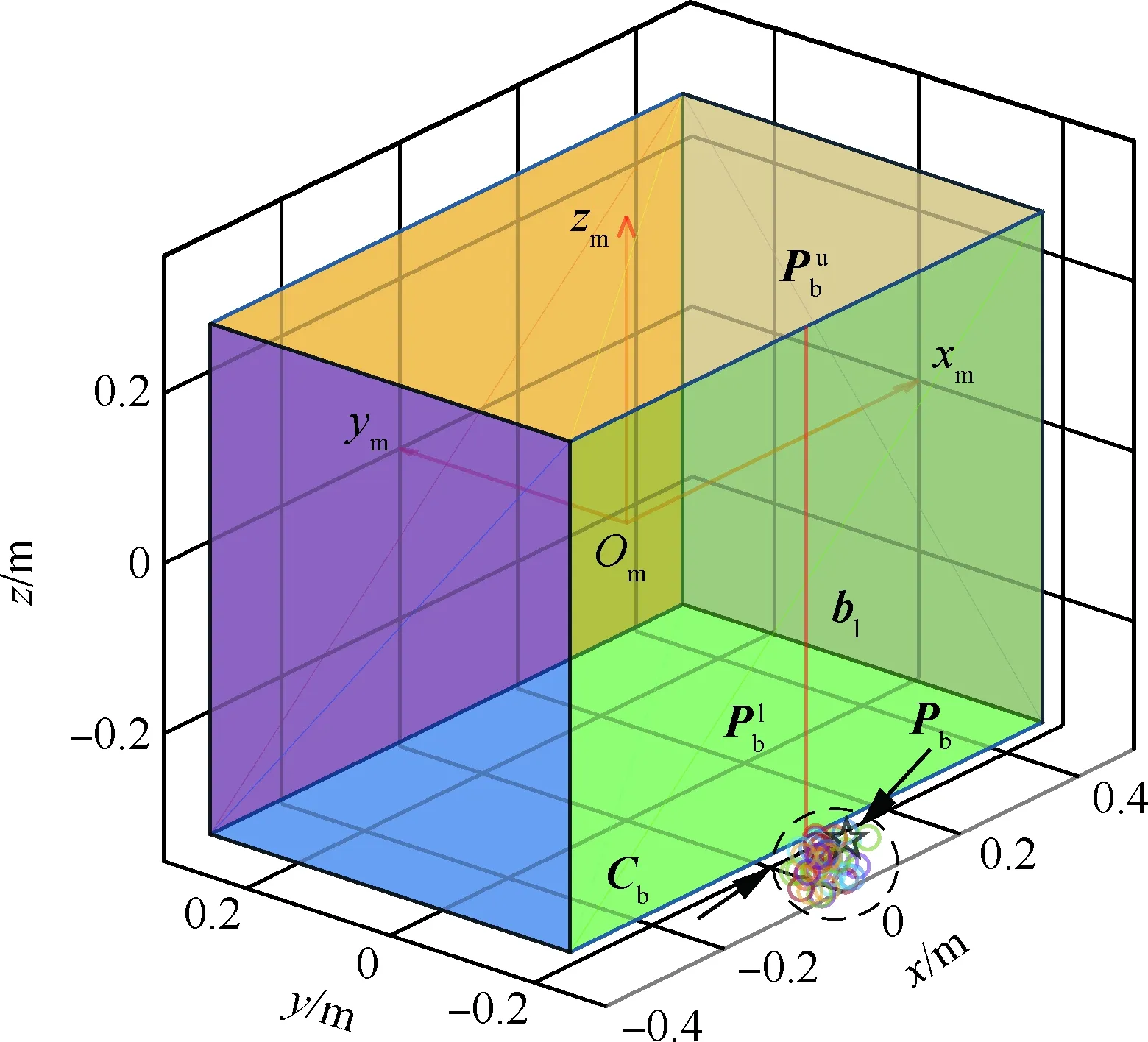
图3 包络元素示意图Fig.3 Caging elements diagram
度εb内的相对于目标静止的所有点的集合,其中包络点Pb∈Cb的选取是随机的。为方便起见,将包络边、包络裕度、包络点集以及包络点统称为包络元素。
(7)
在进行具体的包络算法设计之前,假设多指机构具有诸如底座之类的支撑部件,它可以提供多指机构所需的控制力和控制力矩。
2.1 包络点追踪
为了方便对空间非合作目标实施包络,应当首先实现多指机构与空间非合作目标之间的运动同步,具体为多指机构和空间非合作目标之间的姿态运动同步以及主手指的基关节和包络点之间的平移运动同步。虽然空间非合作目标的运动参数及惯性参数等参数通常未知或含有不确定性,但是已有大量研究来确定这些参数[22],故本文假设空间非合作目标物体的运动参数和惯性参数已知。
关于两航天器之间的相对姿态运动同步控制算法,相关学者已经进行了大量研究,提出了诸如滑膜控制算法[23]之类的成熟算法。因此,可以直接假设在实施包络时多指机构有能力实现与空间非合作目标之间的姿态运动同步。故本文不再赘述多指机构和空间非合作目标之间的相对姿态运动同步的控制算法,直接将其作为实施包络操作的初始条件。

(8)

(9)
(10)
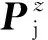
(11)
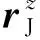

k2sign(x2e)|x2e|α
(12)

(13)
注3在包络点追踪的整个过程中,需要满足多指机构和空间非合作目标物体间不发生碰撞的安全性要求。本文将每一时刻多指机构Od(t)和空间非合作目标物体Om(t)均不能存在交集作为约束来保证两者之间不发生碰撞(式(14))。
Od(t)∩Om(t)=∅
(14)
下面对式(14)做进一步说明。本文中是根据空间非合作目标与多指机构之间的相对几何位置关系来进行碰撞检测的,即通过实时地检测空间非合作目标所占的空间与多指机构所占的空间之间是否有交集来进行判断。具体而言,如果空间非合作目标所占的空间与多指机构所占的空间之间没有交集,则空间非合作目标与多指机构之间不会发生碰撞,是安全的;反之,如果空间非合作目标所占的空间与多指机构所占的空间之间有交集,则说明空间非合作目标和多指机构发生了相互穿插的现象,这显然是不符合实际情况的,属于发生碰撞的情形。式(14)简单明了地表示空间非合作目标与多指机构之间不发生碰撞的安全约束。
2.2 包络边匹配
如图4所示,主手指和包络边之间存在很多可能的匹配构型,引入单向距离D(Cz,bl)来衡量主手指Cz和包络边bl匹配的相似度[25]:
D(Cz,bl)=
(15)
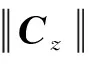
D(cz,i~i+1,bl)=

(16)
式中:Dd(p,bl)表示cz,i~i+1上任意一点到bl的最短距离:
Dd(p,bl)=minq∈blDEuclid(p,q)
(17)
此时,包络边匹配问题可以转化为寻找使得Cz与bl间单向距离最小的主手指关节角θz:
(18)


图5 最优包络边匹配构型搜寻算法Fig.5 Algorithm of optimal caging edge matching
考虑到求解最优化问题(18)的过程中不仅需要实时进行碰撞规避还希望计算效率尽可能高,所以本文采用了快速搜索随机树法来进行求解。快速搜索随机树法是机器人路径规划领域的一个重要的方法,这种方法在机器人规划领域,尤其是高维环境(如,机械臂)的规划中,占有重要的位置,是基于采样的规划方法的一种。如图5所示,首先,通过快速搜索随机树法随机搜索有效匹配构型,但是并不是每个有效匹配构型都会被添加到搜索路径中,只有当前有效匹配构型对应的单向距离比上一个有效匹配构型对应的单向距离小时,才会被添加,这保证了快速搜索随机树法是朝着单向距离越来越小的方向进行搜索的;其次,由于最优匹配构型对应的主手指关节角值是未知的,而传统快速搜索随机树法中目标点是给定的,所以在图5所示的最优包络边匹配构型搜索算法中,以快速搜索随机树法搜索到的相邻2个有效匹配构型所对应的单向距离的差值作为算法是否终止的判断条件;最后,当单向距离收敛到一个稳定值不再变化时,则说明找到了使得主手指与包络边最大程度地相似的主手指关节角取值。虽然快速搜索随机树法搜索每个有效匹配构型的过程是随机的,但是,通过搜索方向和算法终止的判断条件这2个方面保证了优化目标的收敛性,即通过随机搜索找到最好的解。
2.3 从手指构型确定

i≠z,i=1,2,…n,z∈{1,2,…,n}
(19)
然后,根据式(2),确定Ci的可能构型:
(20)

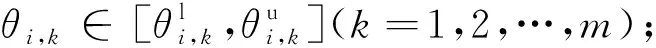
2.4 有效包络构型确定
一旦主手指和所有从手指的构型确定,多指机构的构型Cd也就随之确定:
Cd={Cz,{Ci}}
i≠z;i=1,2,…,n;z∈{1,2,…,n}
(21)
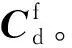
本文所提的“主-从”式的多指机构包络算法,不仅具有处理运动目标的能力,而且在包络构型搜索过程中还简化了系统自由度进而提升了计算效率,所以可以实现对空间非合作目标的快速有效包络。

i≠z;i=1,2,…n;z∈{1,2,…,n}
(22)
3 仿真验证
为了验证所设计算法的有效性,采用图1所示的四指三关节的多指机构分别对可以简化为二

表1 指尖距离的容许范围Table 1 Allowable distances between fingertips
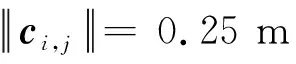

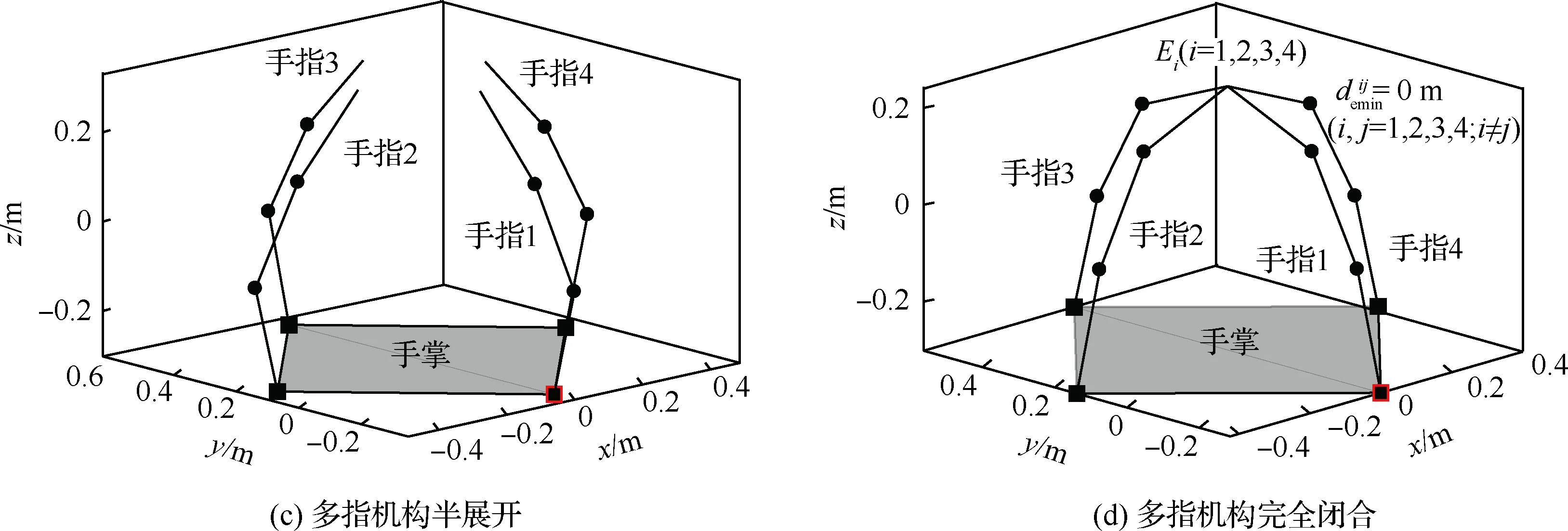
图6 多指机构结构关系图Fig.6 Structural relationship in multi-fingered mechanism
3.1 扁平型空间非合作目标包络
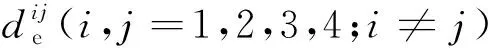
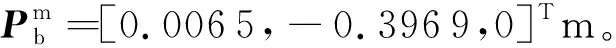

表2 仿真参数Table 2 Simulation parameters
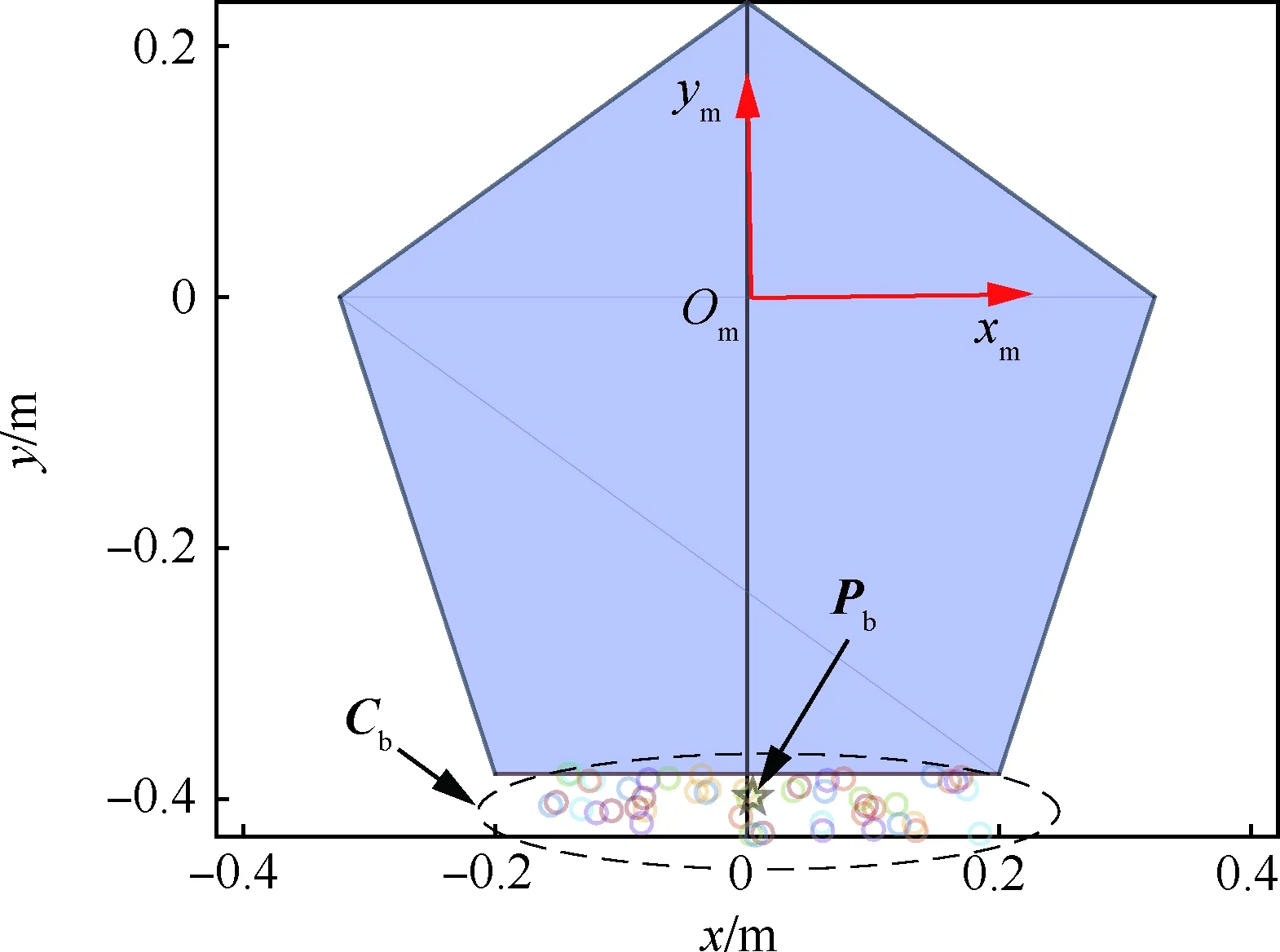
图7 包络正五边形时的包络元素Fig.7 Caging element when caging regular pentagonal object
3.2 一般性三维空间非合作目标包络

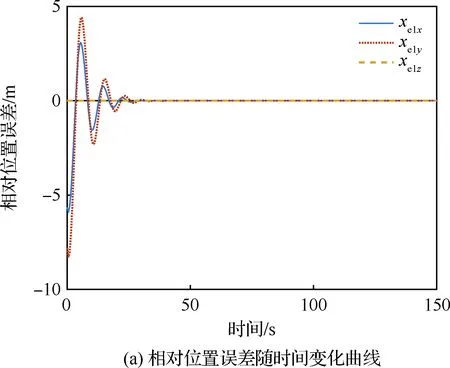
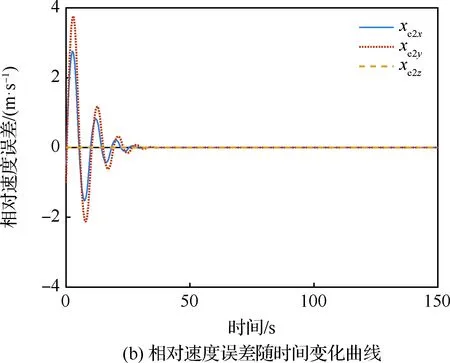

图8 包络正五边形时包络点追踪结果随时间变化图Fig.8 Time responses of caging point tracking results when caging regular pentagonal object
[0,-0.285 1,-0.301 4]Tm。此时,主手指基关节和包络点间的初始相对位置误差为x1e0=[-5.659 5,-7.795 9,0]Tm、初始相对速度误差为x2e0=[0.6,-1,-0.5]Tm/s。同样地,设期望在时刻tb=150 s实现包络点追踪。
通过以上2个仿真案例可以得出,所设计的算法对可以简化为二维平面物体的扁平型空间非合非合目标包络抓捕问题和一般性三维空间非合作目标物体包络抓捕问题均适用,可以高效地得到一条有效的空间非合作目标多指包络抓捕路径。
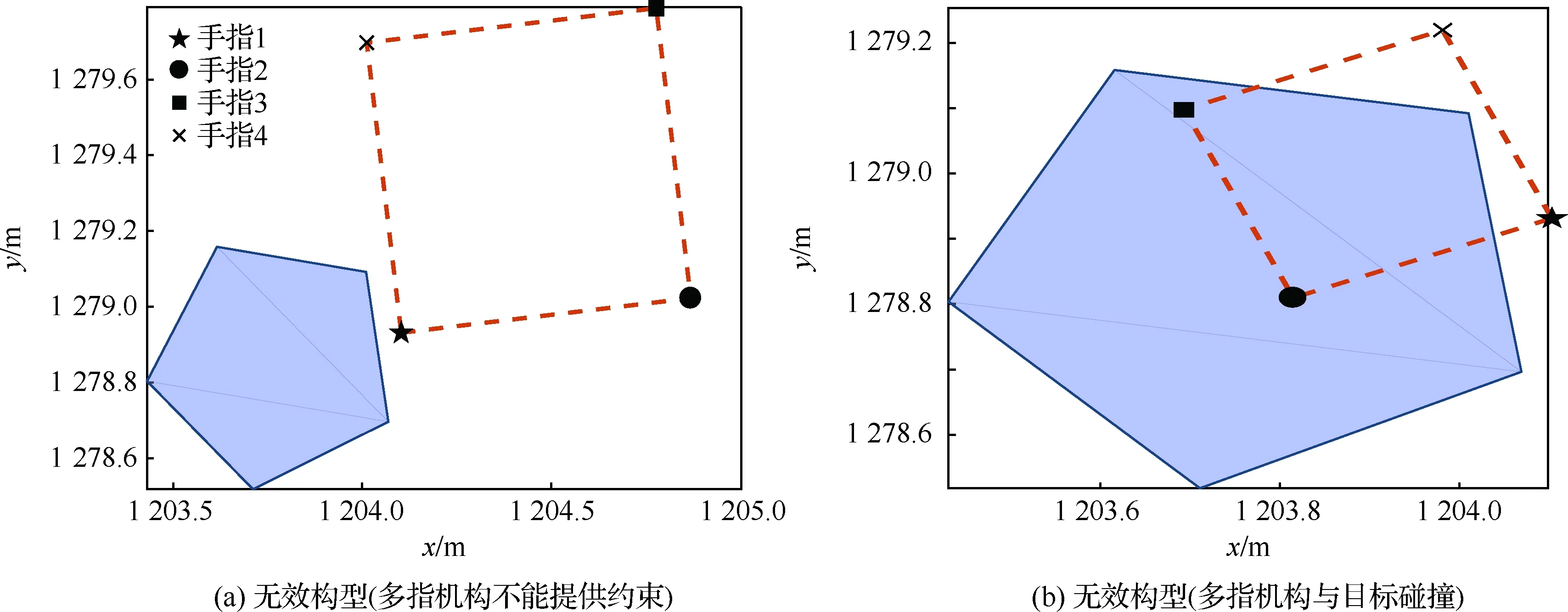
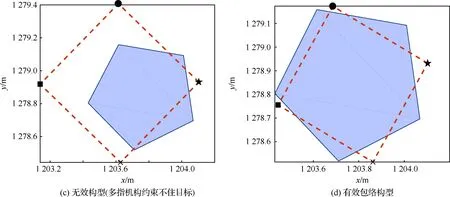
图9 包络正五边形时的多指机构构型Fig.9 Caging configurations of multi-fingered mechanism when caging regular pentagonal object


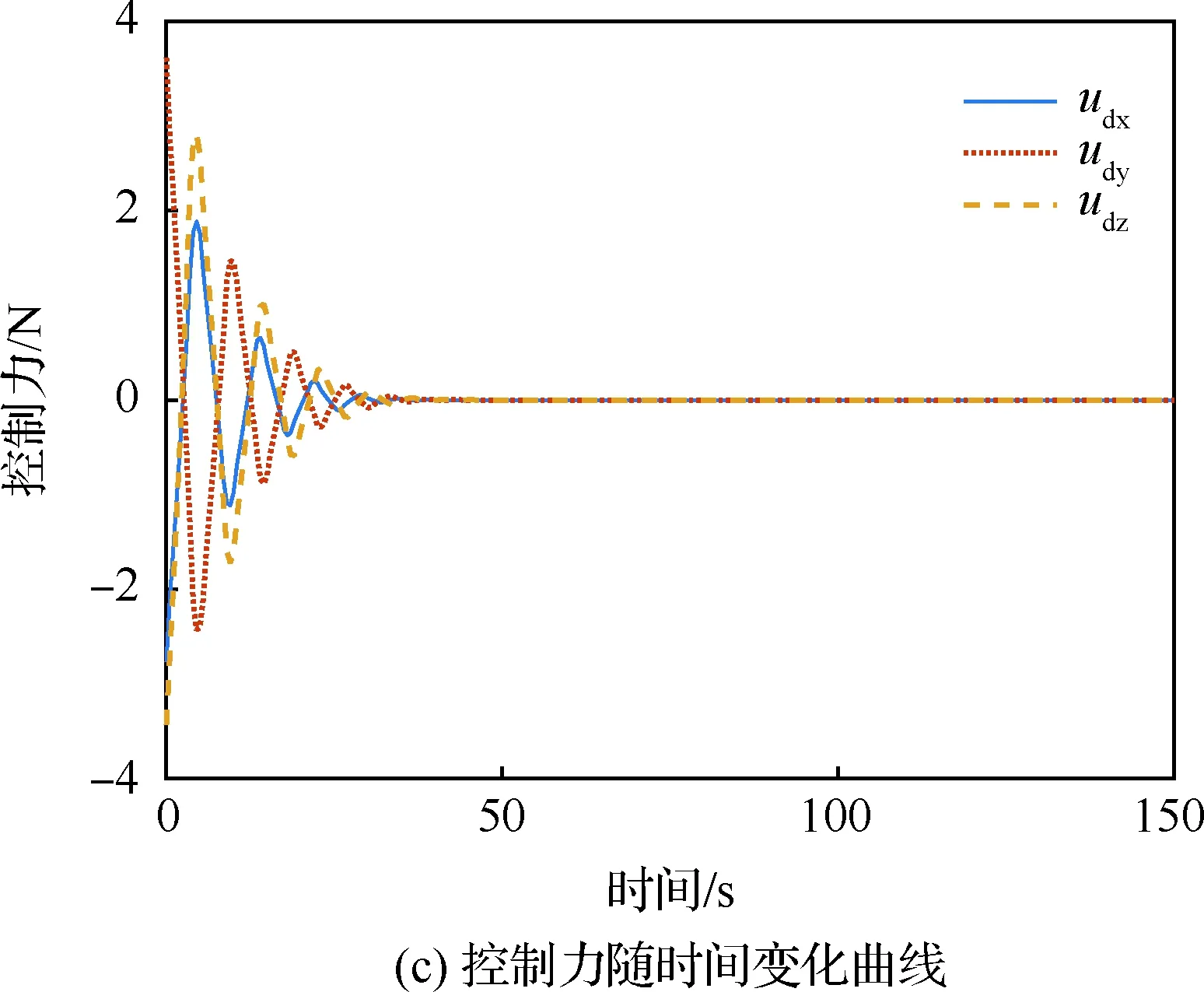
图10 包络长方体时的包络点追踪结果态随时间变化图Fig.10 Time responses of caging point tracking results when caging cuboid object
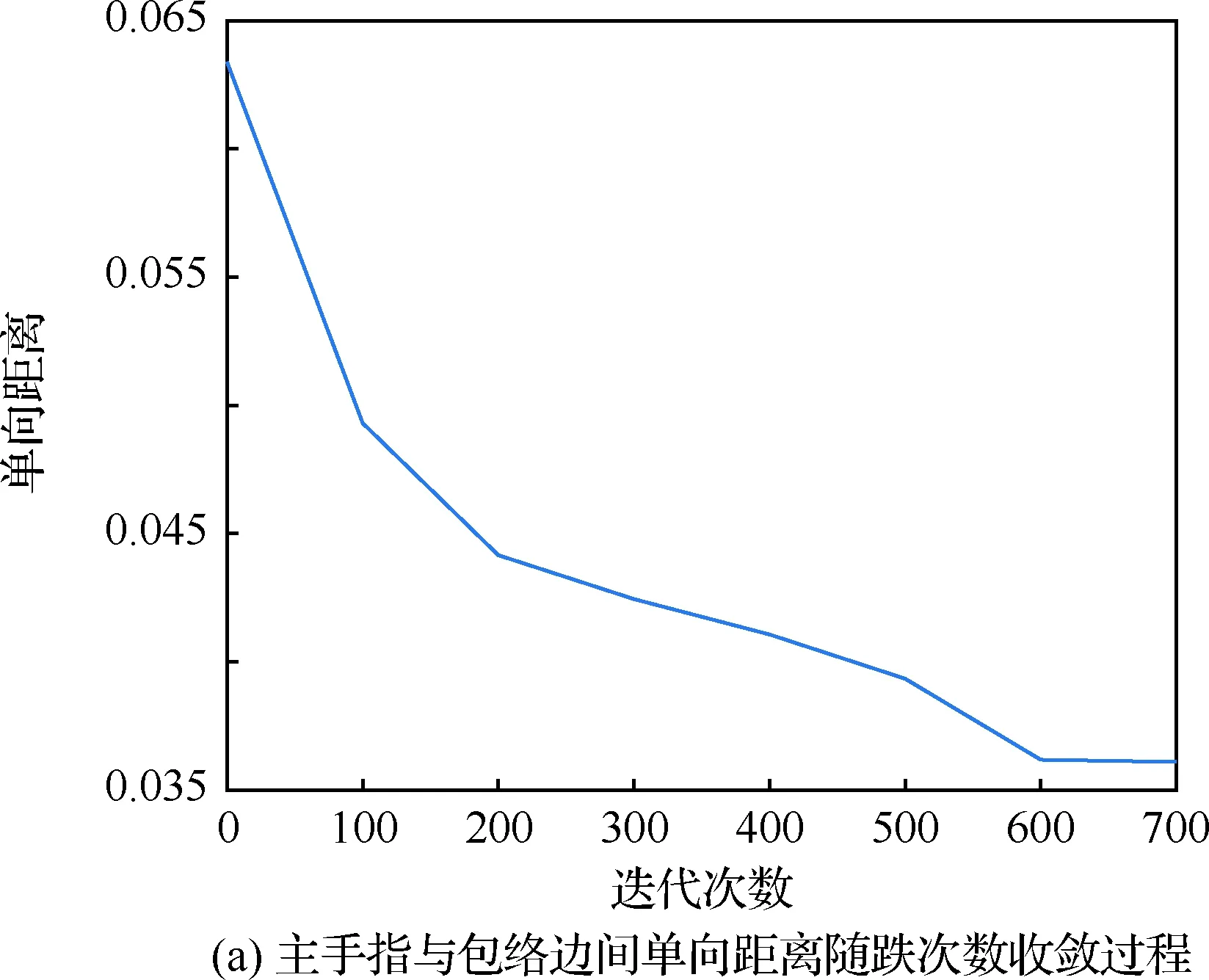
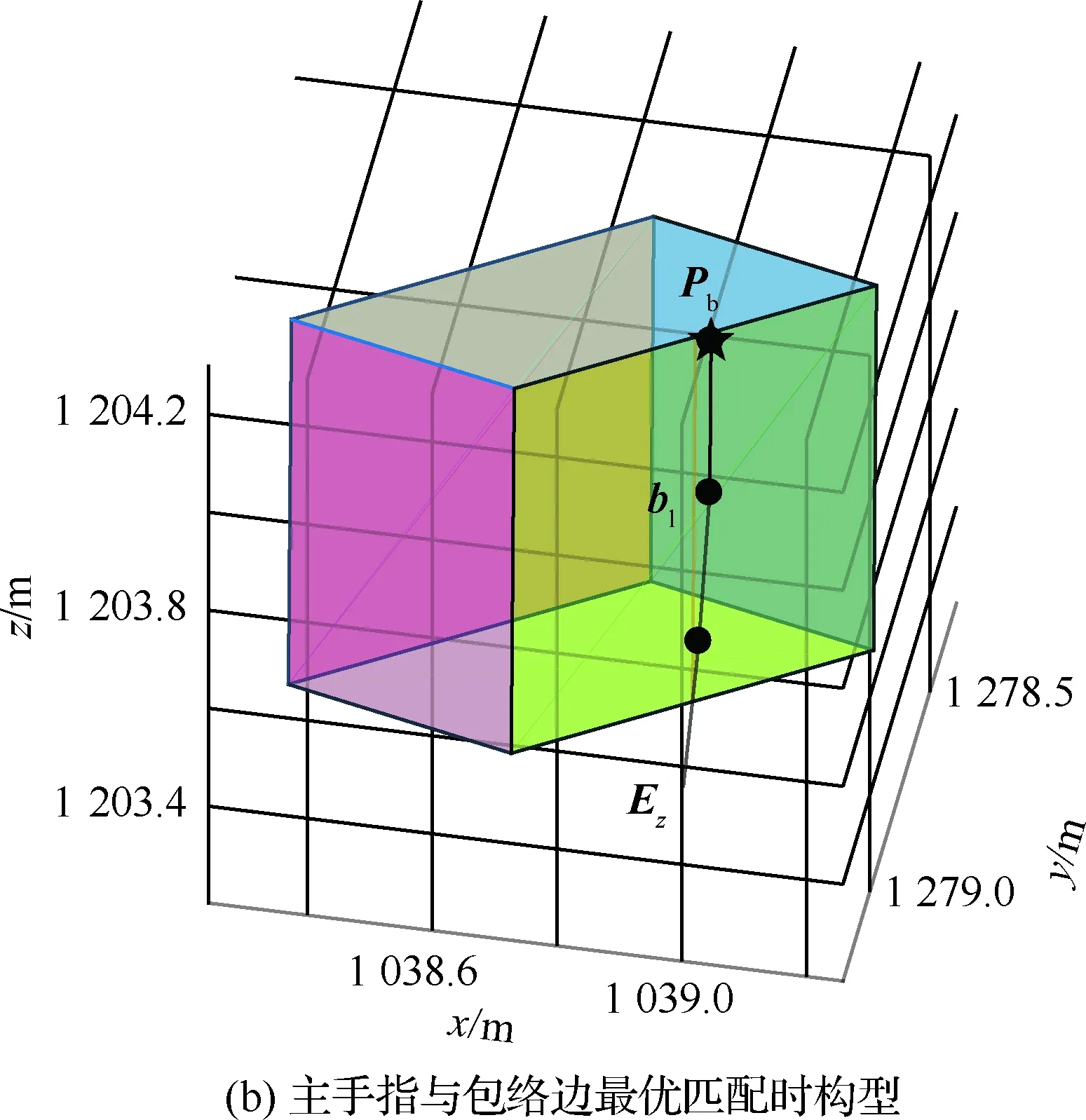
图11 包络边匹配结果Fig.11 Results of caging edge matching
4 结 论
本文针对空间非合作目标抓捕,首先提出了一种多指机构包络抓捕方法。然后,针对多指包络抓捕中存在的多自由度导致的计算复杂问题,以及难以处理动态目标包络抓捕问题,提出了一种“主-从”式多指包络算法,可以高效地得到一条有效的空间非合作目标多指包络抓捕路径。以上抓捕方法和多包络算法的主要创新有以下3点:

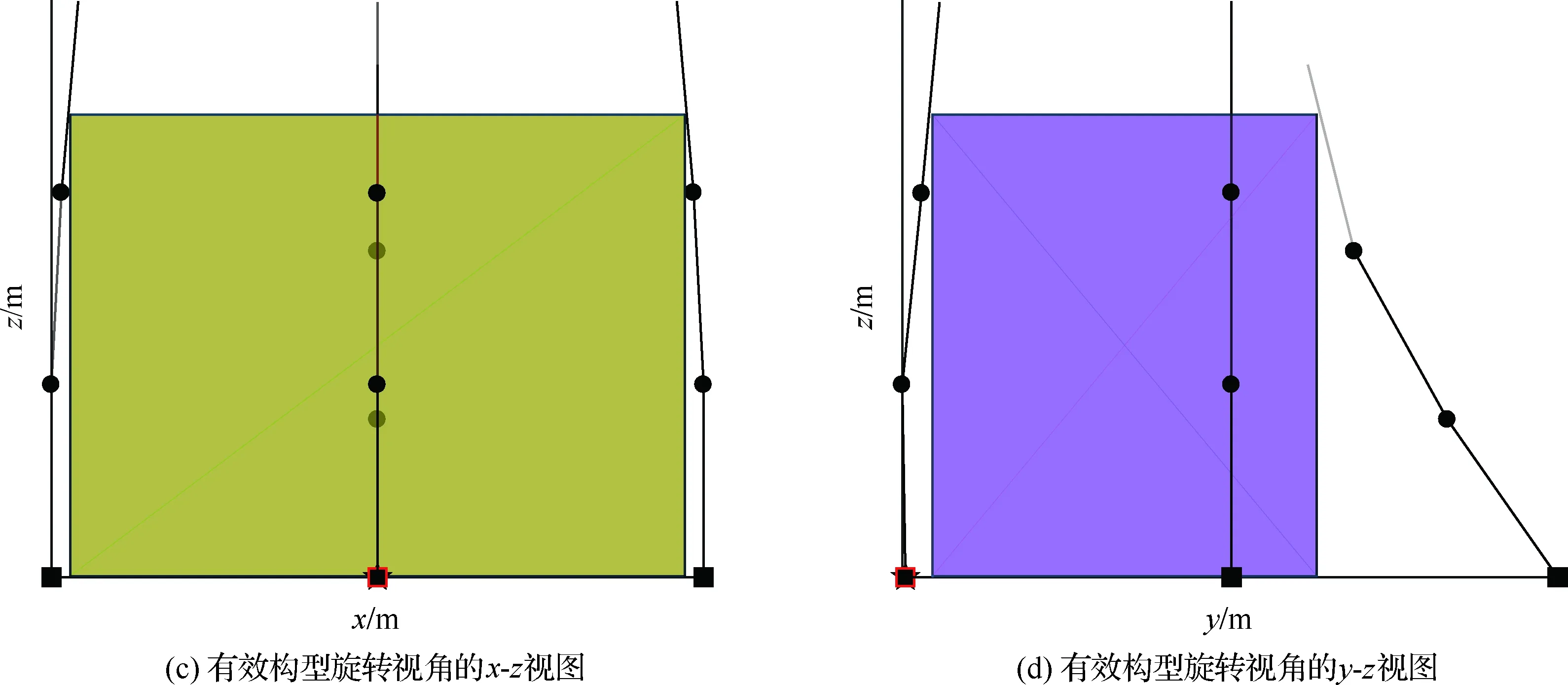
图12 包络长方体时的多指机构构型Fig.12 Caging configurations of multi-fingered mechanism when caging a cuboid object
1) 提出一种多指抓捕建模方法,将多指抓捕机构分为一根主手指和其余从手指两类,针对各类手指分步进行包络算法设计,仿真表明可降低包络构型设计中的自由度,从而可以快速求解包络构型。
2) 采用误差跟踪控制实现主手指的基关节与包络点之间的运动同步,实现了动态空间非合作目标的抓捕。
3) 引入单向距离的概念来定量衡量主手指构型与包络边的相似程度,并建立了考虑了多指机构内在约束的多指机构结构模型,可以利用该模型可以便捷地确定其他从手指的构型。
通过对运动的二维平面物体和三维物体的包络仿真可以得出,所设计的算法不仅简化了计算复杂度,还适用于动态目标。本文所设计的算法可以为后续的对实际空间非合作目标的多指包络抓捕奠定基础。
