智能商用车路径跟踪控制研究

韦宝侣　周恩临　曹文亮

【摘 要】文章建立了商用车电液耦合转向系统模型和车辆二自由度模型。基于车辆二自由度模型和模型预测控制方法进行了商用车路径跟踪控制器设计。电液耦合转向系统、Trucksim和模型预测控制算法联合仿真结果表明，所设计的路径跟踪控制算法保证了车辆良好的跟踪性，其跟踪误差控制在0.01 m之内。

【关键词】商用车;模型预测控制;路径跟踪;电液耦合转向系统

【中图分类号】U469.72;U463.6【文献标识码】A【文章编号】1674-0688（2020）07-0063-03

0 引言

近年來，随着商用车技术不断向着智能化、重型化方向发展，国内外主要商用车公司、相关机构和高校都对先进驾驶辅助系统及搭载该系统的自动驾驶技术进行研究，用以减轻驾驶者的工作负荷，提高车辆驾驶的安全性。

车辆的路径跟踪控制作为自动驾驶的主要分支之一，对自动驾驶的安全性起着至关重要的作用[1]。目前，已经有多种算法应用于路径跟踪控制，比如多点预瞄算法、PID跟踪算法、LQR控制算法和模型预测控制算法[1-4]。模型预测控制可以在线实时计算更新车辆状态信息，它是一种基于最优控制的状态反馈控制法，反馈控制是在有限预测时域内通过迁移的迭代在线优化完成的，控制算法的实时性考虑了外界干扰等因素的作用，从而在横向运动控制中应用广泛并被证实具有良好的控制效果[5-6]。

商用车由于其运行环境简单，主要为港口、码头、封闭园区等，其自动驾驶技术应用有望先于乘用车，同时商用车的自动驾驶是实现队列行驶的基础。

1 转向系统模型

商用车载重非常大，目前普遍采用功率密度较大的液压助力转向（Hydraulic Power Steering，HPS）系统辅助驾驶员。为了能够像EPS（Electric Power Steering，EPS）系统一样具有自动转向功能，在保留液压助力转向器的基础上，于转向管柱处安装了EPS系统，组成电液耦合转向系统（Electro-Hydraulic Coupling Steering，EHCS）系统（如图1所示）。

根据EHCS系统原理，在AMEsim中建立了其仿真模型[7]（如图2所示）。

2 汽车二自由度模型

建立了车辆具有侧向和横摆运动的理想线性二自由度模型（如图3所示）。

根据牛顿第二定理，方程如下：

上式中：kf、kr为前轮和后轮侧偏刚度，a、b为前后轮中心距车辆中心距离，β为质心侧偏角，ωr为车辆横摆角速度，m为车辆质量，v为车辆横向速度，u为车辆纵向车速，Iz为车辆绕z轴转动惯量，δ为车辆前轮转角。

车辆在惯性坐标系X、Y坐标轴上的速度分量：

式中，Ψ（t）为车辆的横摆角速度。

由于车辆的横摆角速度比较小，所以上式可表示如下：

结合车辆二自由度模型和运动学方程，我们将其写成状态向量矩阵的形式：

3 路径跟踪控制算法

3.1 预测模型

线性时变连续方程（7）采用一阶差商的方法进行离散化后，得到离散的状态空间方程：

基于车辆二自由度离散模型进行系统未来时域动态预测，我们假设系统的全部状态都是可以预测的。为了减少或消除系统的稳态误差，我们将式（8）改写为增量的形式：

根据模型预测控制的滚动优化原理，每次将最新得到的值作为系统的初始化值。假设预测时域为P，控制时域为m，应有m≤P，则车辆在控制时域未来一段时间系统的预测控制方程：

上式中，k+i|k（i=1，2，…，p-1）表示在当前k时刻之后预测时域的预测。

根据公式η（k）=C△ζ（k）+η（k-1），预测k+1至k+p时刻的预测输出：

将系统未来时域p步的预测输出用状态向量矩阵的形式表示：

ηp（k）=Sζ△ζ（k）+Iη（k）+Su△U（k）（12）

其中，

3.2 动态优化器

路径跟踪控制的目的是保证车辆良好的跟踪性，即减少车辆横向误差。同时，为了保证平稳转向，我们希望方向盘转角变化不要太大，因此代价函数表示如下：

Qη，i表示根据当前时刻k对预测时刻i的预测控制输出误差的加权因子，其值越大，表明我们期望对应的控制输出越接近给定的参考输入。Ru，j表示根据当前时刻k对预测时刻j的控制增量的加权因子，其值越大，表明我们期望方向盘角度不发生较大的变化，从而保证驾驶的平稳性。

为了避免有约束MPC的最优解带来计算负担，本文采用了无约束MPC来获得一组最优解，根据代价函数和预测方程，无约束MPC优化问题可描述如下：

为了便于求解，我们定义

则代价函数（15）可表示如下：

则预测方程我们可以表示如下：

因此，无约束MPC的优化问题如下：

我们可以求得极值解：

同时根据极值判断条件：

由以上分析知，极值解也是最小解，因此时刻的最优控制解如下：

△U*（k）=（SuTQηTQηSu+RuTRu）-1SuTQηTQηEp（k）（23）

无约束MPC是在每一个时间序列中都能找到最优输入△U*（k），并将最优解的第一个元素作为EHCS系统的输入，则在步产生的状态反馈控制率的控制信号如下：

其中，δ*（k）是作为被控系统的输入量。

随着预测时刻的前移，车辆的状态信息也在变化，求解器根据实时更新的车辆状态信息重新求解最优控制量，然后将每一前移时刻控制器计算出的期望前轮转角作用于EHCS系统，完成模型预测控制的“滚动优化”。

4 基于MPC的商用车横向运动控制仿真

4.1 路径跟踪仿真模型

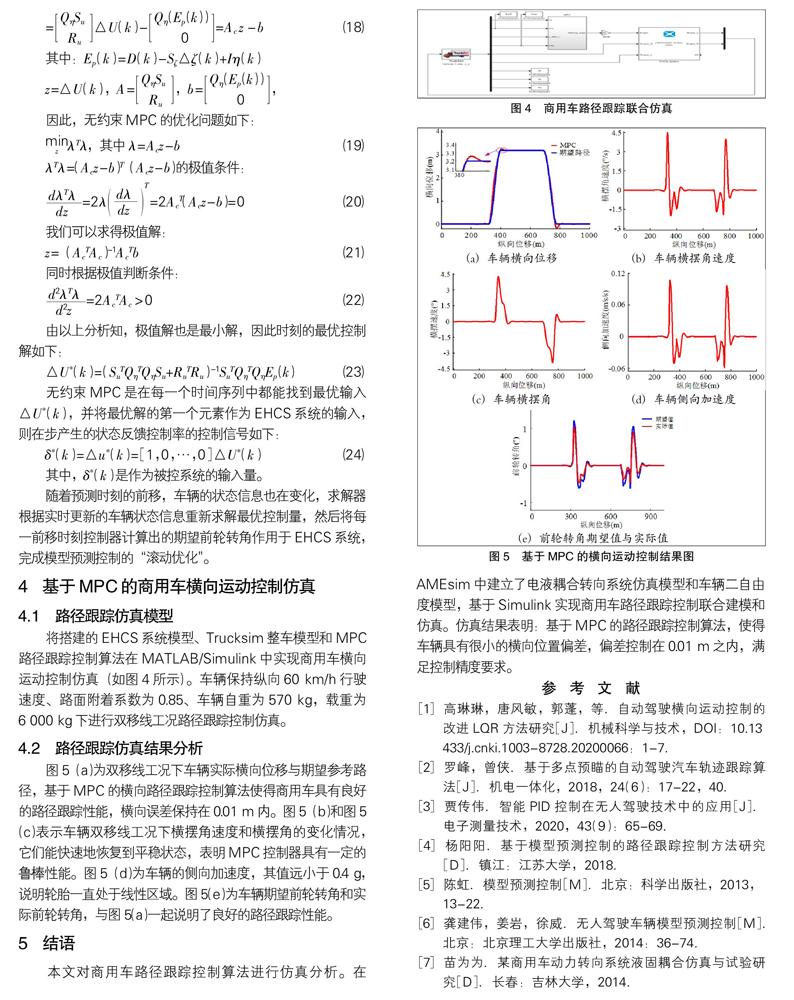
将搭建的EHCS系统模型、Trucksim整车模型和MPC路径跟踪控制算法在MATLAB/Simulink中實现商用车横向运动控制仿真（如图4所示）。车辆保持纵向60 km/h行驶速度、路面附着系数为0.85、车辆自重为570 kg，载重为6 000 kg下进行双移线工况路径跟踪控制仿真。

4.2 路径跟踪仿真结果分析

图5（a）为双移线工况下车辆实际横向位移与期望参考路径，基于MPC的横向路径跟踪控制算法使得商用车具有良好的路径跟踪性能，横向误差保持在0.01 m内。图5（b）和图5（c）表示车辆双移线工况下横摆角速度和横摆角的变化情况，它们能快速地恢复到平稳状态，表明MPC控制器具有一定的鲁棒性能。图5（d）为车辆的侧向加速度，其值远小于0.4 g，说明轮胎一直处于线性区域。图5（e）为车辆期望前轮转角和实际前轮转角，与图5（a）一起说明了良好的路径跟踪性能。

5 结语

本文对商用车路径跟踪控制算法进行仿真分析。在AMEsim中建立了电液耦合转向系统仿真模型和车辆二自由度模型，基于Simulink实现商用车路径跟踪控制联合建模和仿真。仿真结果表明：基于MPC的路径跟踪控制算法，使得车辆具有很小的横向位置偏差，偏差控制在0.01 m之内，满足控制精度要求。

参 考 文 献

[1]高琳琳，唐风敏，郭蓬，等.自动驾驶横向运动控制的改进LQR方法研究[J].机械科学与技术，DOI：10.13433/j.cnki.1003-8728.20200066：1-7.

[2]罗峰，曾侠.基于多点预瞄的自动驾驶汽车轨迹跟踪算法[J].机电一体化，2018，24（6）：17-22，40.

[3]贾传伟.智能PID控制在无人驾驶技术中的应用[J].电子测量技术，2020，43（9）：65-69.

[4]杨阳阳.基于模型预测控制的路径跟踪控制方法研究[D].镇江：江苏大学，2018.

[5]陈虹.模型预测控制[M].北京：科学出版社，2013，13-22.

[6]龚建伟，姜岩，徐威.无人驾驶车辆模型预测控制[M].北京：北京理工大学出版社，2014：36-74.

[7]苗为为.某商用车动力转向系统液固耦合仿真与试验研究[D].长春：吉林大学，2014.