地域差异下工资分配额度定量表征模型研究

李康康，梁锦钰，吴蒙，王璐，张彩军,

(1.华北理工大学 冶金与能源学院，河北 唐山 063210；2.华北理工大学 学科建设处，河北 唐山 063210)

国有企业工资总额管理是调节国家、企业、职工三者利益关系的重要方式，是深化国有企业工资分配机制改革的核心。企业的工资总额分配机制对企业的发展至关重要，它不仅影响员工的激励、调控和保障管理，而且有助于企业实现战略目标、改善经营绩效、提高市场竞争力和加强企业文化。处理好工资总额分配问题，对企业的发展至关重要。

而影响工资分配的因素有很多，具有随机性、模糊性和未知性的特点。根据统计数据的数量和性质，运用灰色系统理论的方法对不确定问题进行研究。针对某国有企业与不同省市分公司分配工资问题，通过与各省市地区构建差异相关联的收入与成本规模、收益等相关指标，建立一套科学合理的工资总额分配方案，并将其应用于大型连锁企业中。

1 分析影响工资分配的主要因素

1.1 研究思路

在实践中，系统内部的影响因素具有很大的随机性。此时，应采取适当的数据处理方法，比较各组成部分之间的联系程度，突出重点，抓主干，消除次要影响因素。工资分配机制受多种因素影响，在不同影响因素的定义区间内，各因素对分配量的影响是不同的。在应用数学领域，对于所研究信息的部分确定、部分模糊且存在不确定性现象的系统，通常以灰色系统理论为基础进行研究。灰色理论系统是研究“部分信息和部分信息未知”的“小样本”和“弱信息”不确定性系统[1]。通过生成和开发一些已知信息，提取有价值的信息进行研究，从而正确描述和有效控制系统的运行规则[2]，通过对原始数据的处理和系统变化规则的挖掘，凭借相应的微分方程，建立抽象系统发展的动态模型。根据已知数据，运用灰色系统理论建立灰色关联度模型，并对各指标和评价量指标进行了关联度分析。

1.2 工资分配额关联度模型

1.2.1参考数列和比较数列

根据灰色关联分析法，将影响工资分配的16个影响指标视为一个灰色系统，每个影响指标为该系统的一个因素。把26个地区设为参考数列，地域人口、城乡居民人均收入、城乡人均消费支出、城镇居民数、城镇居民收入、城镇居民人均可支配收入、GDP、其他国有企业在岗职工平均工资、商品房平均销售价格、业务总收入、业务总成本、生产用固定资产、净资产收益率、人事成本费用率、劳动生产率、成本费用率为比较数列，组成指标矩阵{Pi(K)|i=1,2,…,16}，表示为P={P1(K),P2(K),…,P16(K)}。

1.2.2 数据无量纲化处理

由于各指标的单位不同，不同量纲之间比较的意义不明确，所以首先对数据进行无量纲处理，所采用的无量纲方法有：

(1)

无量纲后的矩阵仍记作：

(2)

1.2.3 关联系数及关联度的计算

令△P(K)=|P0(K)-Pi(K)|，其中η取0.5，关联度为每组关联系数的均值，将其作为每组最终影响工资分配的关联大小，关联度为：

(3)

(4)

1.2.4 模型求解

运用SPSS对各个指标关联度进行降维因子求解，将地域人口、城乡居民人均收入、城乡人均消费支出、城镇居民数、城镇居民收入、城镇居民人均可支配收入、GDP、其他国有企业在岗职工平均工资、商品房平均销售价格、业务总收入、业务总成本、生产用固定资产、净资产收益率、人事成本费用率、劳动生产率、成本费用率分别表示为X1，X2，…，X16。按照灰色关联度计算得到图1所示影响工资分配各指标关联度分布。

图1 影响工资分配各指标关联度分布

1.3 结果分析

相关系数r是测定变量之间线性相关程度和相关方向的代表性指标。相关程度判定的标准是：如果r=0，则两变量不相关；如果|r|∈(0,0.3]，则两变量为弱相关；如果|r|∈(0.3,0.5]，则两变量为低度相关；若|r|∈(0.5,0.8]，则两变量为显著相关；若|r|∈(0.8,1]，则两变量为高度相关；若|r|=1，则两变量为完全相关。相关方向判定的标准是：如若r>0，则两变量变化的方向一致，即是正相关；如若r<0，则两变量变化的方向相反，即是负相关[3]。

如图1所示，其他国有在岗职工工资、商品房平均销售价格、净资产收益率、人事成本费用率与工资分配总额呈低度相关；城乡居民人均收入、城乡人均消费支出、城镇居民人均收入可支配收入、劳动生产率、成本费用率与工资分配总额呈显著相关；地域人口、城镇居民数、城镇居民收入、GDP、业务总收入、业务总成本、生产用固定资产与工资分配总额呈高度相关。

2 构建工资分配模型

经过对数据的整理分析以及处理，最终选取解释变量有地域人口、城镇居民数、城镇居民收入、GDP、业务总收入、业务总成本、生产用固定资产。根据以上因素，采用多元线性回归分析对国有企业工资分配总额的分配模型进行构造[4]。回归分析是从一组样本数据出发，确定变量之间的数学关系式，对关系式的可信程度进行统计检验，并分辨出解释变量对被解释变量的影响效果以及显著程度[5]。利用所求关系式，根据一个或几个变量的取值来预测或控制另一个特定变量的取值，并给出这种预测或控制的精度的一种有效方法[6-8]。

2.1 多元线性回归方程的确立

Y=a+b1x1+b2x2+b3x3+…+ξ

(5)

其中：

Y代表各省市分配的工资总额；a代表常量；

x1、x2、x3…代表主要影响因素；

b代表各因素的模型回归系数；

ξ代表随机误差项。

2.2 多元线性回归方程的应用

根据计量经济学关于最小二乘法原理的解释，进入线性回归的自变量之间以各自变量与因变量之间的关联度是影响模型估计质量的重要因素。其尤为重要的就是相关系数权重。表1所示为回归分析模型的归总情况。表2所示为共线性检验结果。

表1 回归分析模型归总

从上表1中可以看出，进入模型的变量其调整的决定系数为0.981，课件模型拟合效果较为理想。

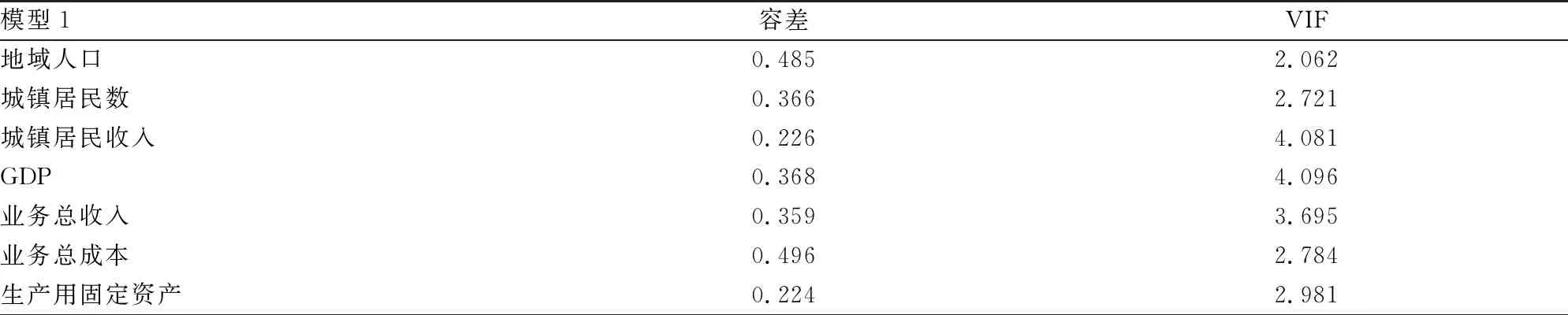
表2 共线性检验

根据表2的共线性检验可以看出，所有变量的容差都大于0.1，VIF值也较小，说明模型的共线性问题较小，说明整体模型回归效果较为良好。将各数据代入多重线性回归模型假设公式中为：

(6)

图2所示为基于关联度下的原分配额度与优化后分配额度的拟合趋势图。

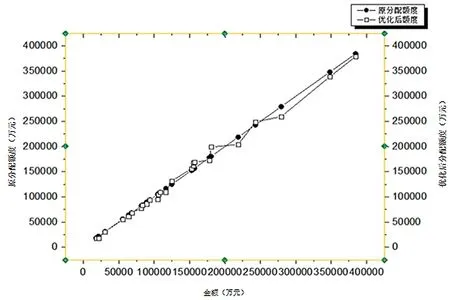
图2 拟合曲线

通过图2精度计算评定可知，2条曲线的拟合程度基本一致，说明此分配方案曲线模型相对科学，具有合理性。

2.3 结果分析

图3(a)所示为不同省区下地域人口与工资分配总额关系图，图3(b)所示为不同区域业务总收入与生产用固定资产与分配的工资总额关系图

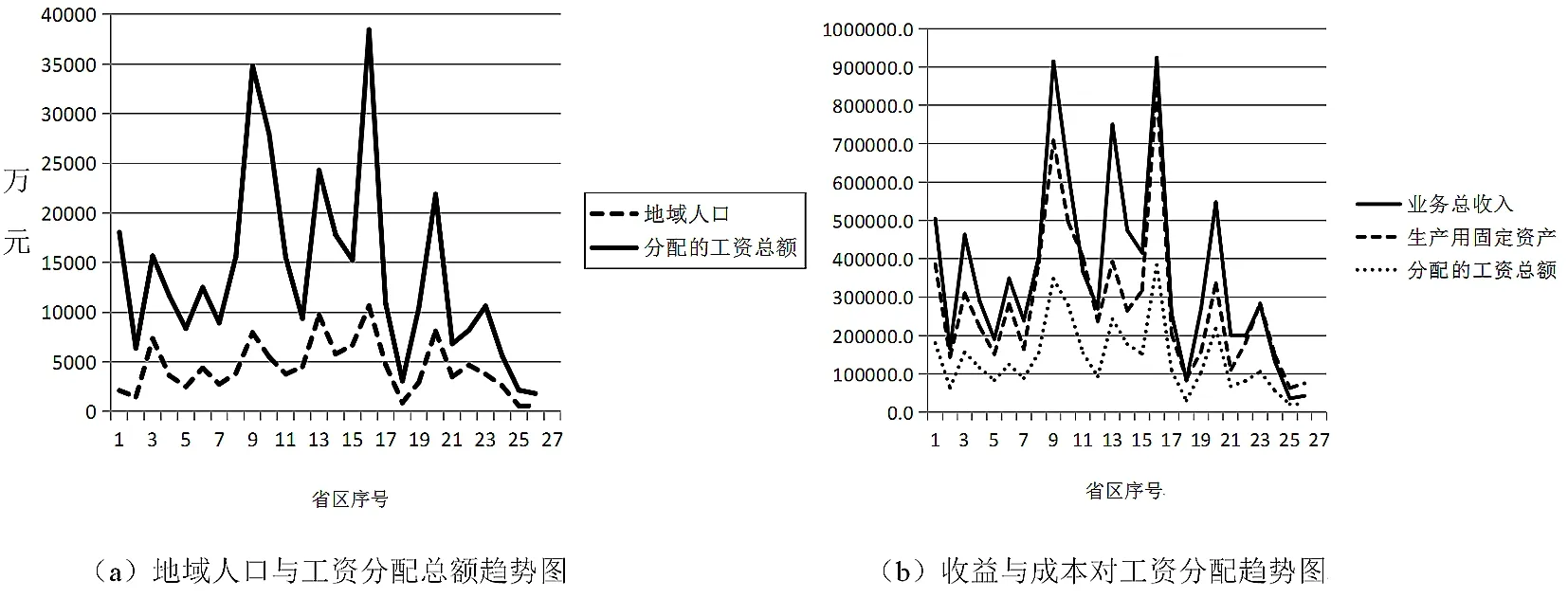
图3 趋势与走向

由图3(a)可知，地域人口与工资分配总额呈现正相关态势。说明国企对人才的吸纳和依赖仍集中于大城市和多数城镇地区，优秀技术人才是一个企业得以壮大的资本。而人才数量越来越成为企业经济效益的重要指标之一，效益与员工的薪资直接挂钩。

由图3(b)可知，业务总收入、业务总成本和生产用固定资产与分配的工资总额呈正相关，说明提高国企总产值是企业生存和发展的迫切需要。只有建立符合市场规律的工资分配体制，才能使企业长久发展。

3 结论

(1)依据地域人口、城镇居民数、城镇居民收入、GDP、业务利率率和资产利润率等主要因子，构建系统化工资分配模型，具有指标选取可靠，反映综合性强的优势。

(2)采用回归分析等统计数学模型，并结合数据信息，针对整合后的数据进行可视化处理、统计与因子分析，在直观分析工资分配总额与相关数据信息之间相关性同时，借助统计学参数，微观透视各指标数据对工资分配总额的作用强度。建立了工资分配总额与其主要影响因子之间的定量函数关系，确保所建立的回归方程的实效性。