基于IGA-ELM的高炉铁水硅含量预测
2020-12-26孙洁崔婷婷徐彬王兴楠
孙洁,崔婷婷,徐彬,王兴楠
(1. 华北理工大学 电气工程学院,河北 唐山 063210;2. 首钢京唐钢铁联合有限责任公司 炼铁部,河北 唐山 063210)
高炉炼铁过程是一个连续进行的动态反应过程,具有时变、非线性、多尺度、大时滞等特征,因其内部高温、高压、强腐蚀和强干扰等环境,很难通过直接测量获得内部的热状态[1]。鉴于铁水硅含量和炉温的相关性,一般通过铁水硅含量间接地反映炉内温度的变化[2]。因此,为了有效地控制炉温,保证高炉的稳定运行要及时掌握铁水硅含量及其变化趋势。
20世纪80年代以来,人工神经网络(Artificial Neural Network,ANN)成为人工智能领域的研究热点。其通过对人类大脑的神经元网络进行抽象来处理问题,根据不同的连接方式建立不同的网络,从而构建一种简单的模型[3]。近年来,随着ANN不断的深入研究,使得其在许多领域都成功地解决了现代计算机都很难解决的实际问题,尤其是在模式识别、自动控制、智能机器人、预测估计、医学、生物和经济等领域均表现出了良好的智能特性[4]。ELM[5,6]是一种新型的单隐含层前馈神经网络,其在2004年由南洋理工大学的黄广斌提出,有效地解决了反向传播算法(Backward Probagation,BP)存在学习效率低以及参数设定繁琐等问题。但是ELM的输入层权值和隐含层阈值随机产生,对算法的预测速度和预测精度会产生影响,针对ELM存在的问题,许多研究人员做了深入研究,提出了大量的智能算法来优化ELM的参数,并都取得了很好的效果[7-10]。根据对前人研究成果的分析,提出了利用IGA优化ELM的输入层权值和隐含层阈值,来进行高炉铁水硅含量预测,并通过MATLAB仿真与单一的ELM预测模型进行对比,来验证IGA-ELM预测模型的有效性。
1 IGA-ELM模型的建立
1.1 ELM基本原理
如图1所示,ELM的结构由输入层、隐含层和输出层三部分组成,其算法描述如下:
任意给定n个不同的样本(xi,ti),i=1,2,…,n,其中,存在n个输入层神经元xi=[xi1,xi2,…,xin]T∈Rn,m个输出层神经元ti=[ti1,ti2,…,tim]T∈Rm,隐含层节点有k个,则ELM网络模型可以表示为:
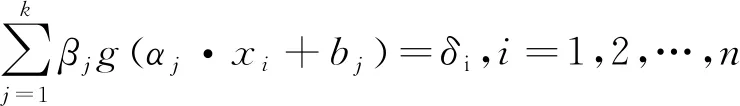
(1)
在式(1)中,αj=[αj1,αj2,…,αjn]为输入层节点连接第j个隐含层节点之间的输入权值向量,bj为第j个隐含层节点的阈值,βj=[βj1,βj2,…,βjn]为第j个节点连接输出节点的权值向量,δi=[δi1,δi2,…,δim]T为ELM的预测输出值。
ELM的目的是使输出误差为最小值,则公式可以表示为:
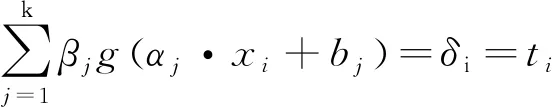
(2)
则式(2)简化为:
Hβ=T
(3)
激励函数g(x)为无限可微时,β可以通过求解最小二乘解获得,其公式为:
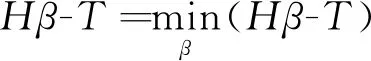
(4)
其解为:
(4)
在式(5)中,H*为矩阵H的Moore-Penrose广义逆。
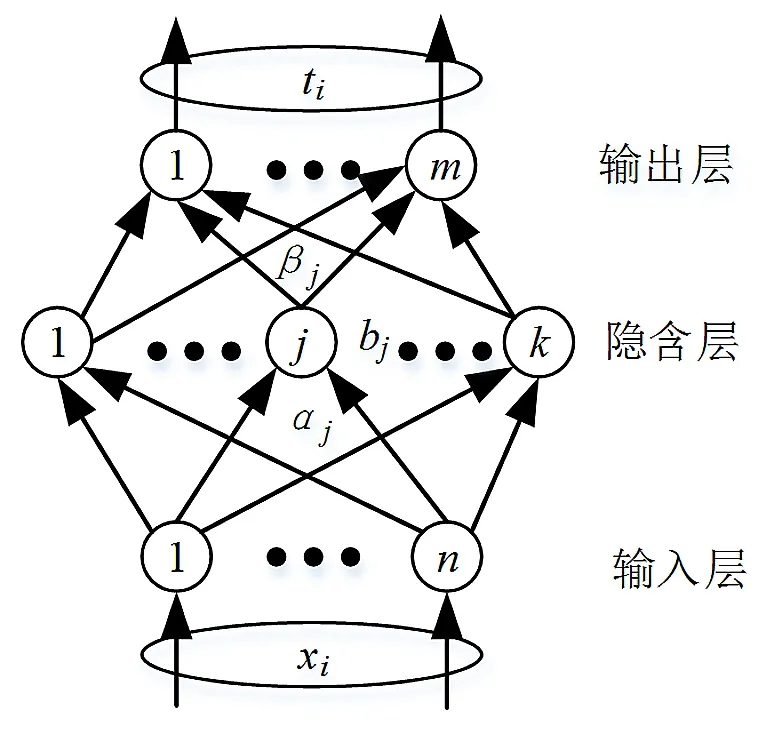
图1 ELM网络结构图
1.2 IGA对ELM的优化
免疫算法是对生物体免疫机制的抽象表达,求解的问题是抗原,对应的解是抗体,抗原和抗体的亲和度体现了可行解与最优解的逼近程度[11]。免疫遗传算法是将遗传算法与免疫算法相结合,其既具有遗传算法的特性又具有抗体浓度的调节机制,避免了遗传算法在后期易出现退化现象的问题,增强了算法的收敛速度和搜索性能。图2所示为IGA-ELM基本流程图,其运算过程如下:
(1)将ELM的连接权值和阈值作为IGA的抗原进行编码。
(2)初始种群由随机产生的M个抗体构成。
(3)将ELM的均方根误差(Root mean square error,RMSE)作为IGA的适应度函数,即:
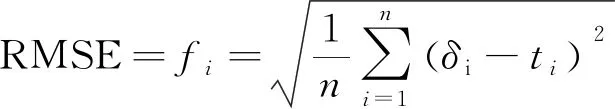
(6)
在式(6)中,fi为第i个粒子的适应度函数,δi为样本预测值,titi为样本实测值,n为输入数据总数,适应度值越小,预测精度越高。
(4)判断算法是否满足终止条件,若获得了设置的最优值或到达了最大迭代次数,则停止迭代,转到步骤(7),否则转到步骤(5)。
(5)将当前种群中抗体的亲和力进行遗传操作,从而产生子代种群:
a.在进行选择操作时常用轮盘赌选择方法,在该方法中,其适应度值与个体被选择的概率成比例,设M为群体规模,个体i的适应度值为fi,则个体被选择的概率为:
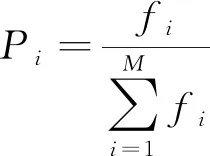
(7)
b.交叉操作是通过替换重组2个父代个体的部分结构而形成新的个体。交叉运算可以增加算法的搜索性能。交叉时常用实数交叉方式,其公式为:
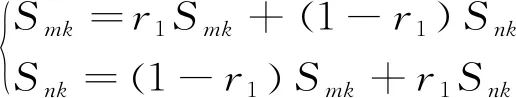
(8)
在式(8)中,r1为(0,1)之间的随机数,Smk和Snk分别为第m和第n个染色体在第k位上的交叉操作。
c.变异操作是变动群体中的个体串的某些基因座上的基因值,通过变异操作可以增加种群的多样性,其公式为:
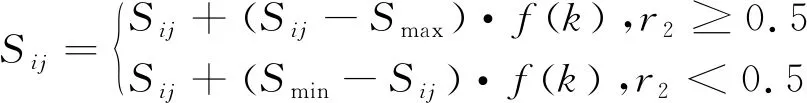
(9)
f(k)=r3(1-k/kmax)2
(10)
在式(9)和式(10)中,基因Sij的上下界分别为Smax和Smin,r2和r3为(0,1)之间的随机数,k和kmax分别为当前和最大的迭代次数,f(k)为变异概率。
(6)更新种群:将子代种群作为当前种群,且产生记忆抗体,转到步骤(3)继续进行迭代。
(7)输出最优权值和阈值,建立IGA-ELM模型,将该模型用于实验的训练和预测。
2 实例仿真
2.1 输入变量的选择及数据预处理
实验数据选自某钢厂1号高炉,由于高炉内反应复杂,众多变量都和硅含量的变化有着密切的关系,若模型的输入变量过多会使模型变得复杂,过少又会降低模型预测的精度,因此根据相关性分析选取与硅含量变化较大的7个变量作为模型的输入变量,分别为:透气性指数、炉顶压力、喷煤率、压差、热风压力、炉顶温度以及前一炉硅含量。
实验选取400组原始数据,经过剔除异常值、滞后步数处理以及一段时间内取平均得到270组数据,随机选取200组数据进行模型的训练,剩余70组数据进行预测。
2.2 模型评价指标
为了对模型的预测精度进行评价,采用2个指标来进行分析,分别为预测命中率(Hit rate,HR)和均方根误差(Root mean square error,RMSE),其中HR越大,RMSE越小,说明模型的预测精度越高,公式如下:
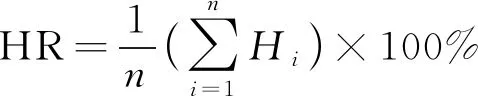
(11)
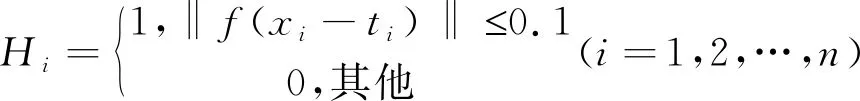
(12)
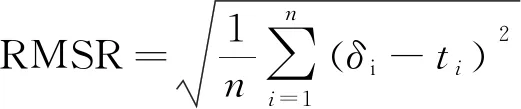
(13)
2.3 实验结果及分析
图3所示为ELM模型对铁水硅含量预报结果图,图4所示为GA-ELM模型对铁水硅含量预报结果图。由图3和图4可以看出,在硅含量变化比较平稳时,ELM模型和IGA-ELM模型的预测效果均较好,但在硅含量波动较大时,IGA-ELM模型的预测效果明显优于ELM模型,而且随着炉次的增加,IGA-ELM模型的预测值能够更好地跟踪实测值的变化,说明IGA-ELM模型的学习能力和泛化性能均高于ELM模型,而且IGA-ELM模型具有更高的稳定性。
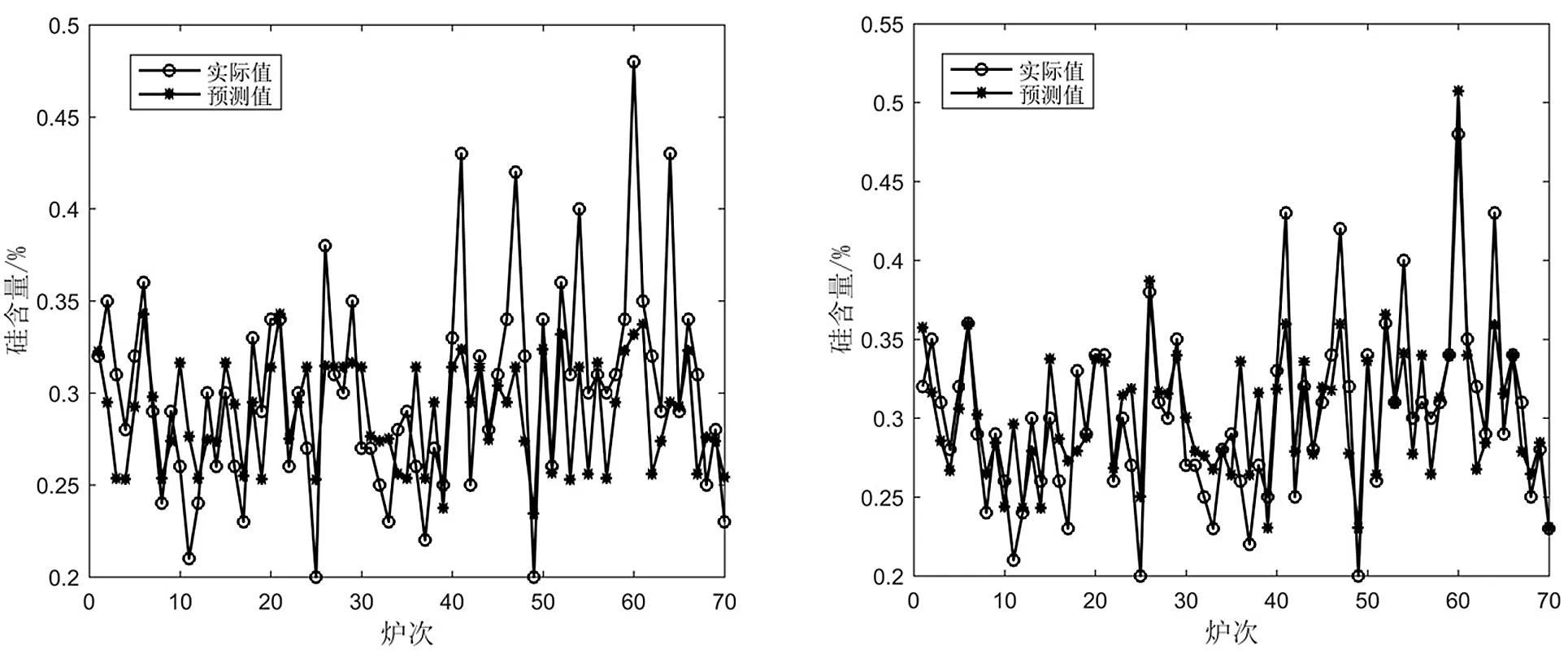
图3 ELM模型铁水硅含量的预报图 图4 ELM模型铁水硅含量预报图
表1所示为不同模型的铁水硅含量预报结果对比。由表1可以看出,IGA-ELM模型的预测命中率相比于单一的ELM模型提高了10%左右,且其均方根误差降低了0.011。由此可知,使用免疫遗传算法优化后的IGA-ELM模型的预测精度有了明显的提升。

表1 不同模型的铁水硅含量预报结果对比
3 结 论
(1)免疫遗传算法有效地解决了遗传算法在后期易出现退化现象,增加了抗体群的多样性,避免了陷入局部最优解,提高了全局寻优能力。
(2)使用免疫遗传算法来优化极限学习机的权值和阈值,使预测模型的泛化性能、学习能力以及预测精度均有所提高,并且增加了模型的稳定性,优化后的模型可以有效地为高炉实际操作提供指导。
