泵用转子上限形状系数的统一计算模型
2020-12-25
(宿迁学院,江苏宿迁 223800)
0 引言
转子泵是一种利用泵内容积的变化来输送介质的容积泵,其中齿轮泵和罗茨泵是最典型的转子泵,应用极其广泛[1-2]。由于泵内容积的变化是通过转子副的旋转运动来实现的,为此,转子的轮廓特征决定了泵内容积的变化特性,即转子轮廓直接决定了泵的性能[3],其轻量化设计业已成为一种趋势。现有研究结果表明转子的形状系数越大,泵整体性能尤其轻量化性能越好[4-5],这其中势必涉及到形状系数的上限问题。目前,虽然由“角点”状态下的几何分析给出了常见圆弧转子的上限形状系数[6],由渐开线终端点位于基圆上的几何分析,给出了常见渐开线转子的上限形状系数[7],但这一针对具体型线下的个案方法,不具普适性,且所涉理论广,既不利于一般工程技术人员的直接采用,也不利于转子创新型线的上限形状系数预测,虽然由“角点”处曲率半径等于0的状态,给出了最大形状系数的计算方法[8],但也存在最小曲率半径不等于0的状况[9]。为此,旨在文献[8]的基础上,通过形状系数上限取得条件的进一步研究,以期获得转子上限形状系数的统一计算模型。
1 转子轮廓与工作轮廓
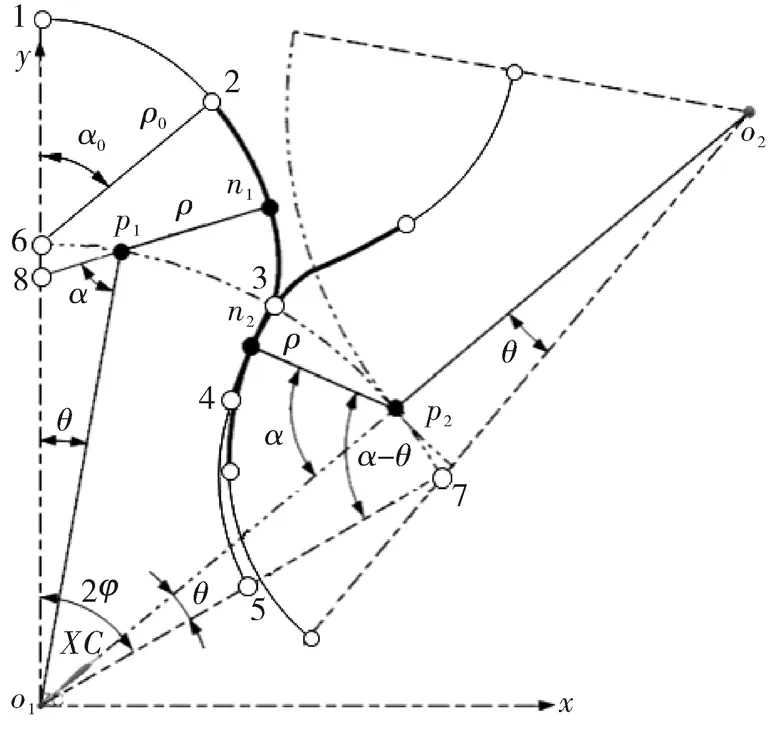
图1 工作轮廓及共轭关系
记 ∠1o13=∠3o15=φ=0.5π/N,∠162= α0、的长度=ρ0为工作轮廓的起始法角、起始法长。则,转子的形状系数 ε 为:

图1中,设主(中心为o1)、从(中心为o2)转子在主转子上的点n2(x2,y2)处共轭。由于主、从轮廓完全一致,则从轮廓上的点n2对应于主轮廓上的点为n1(x1,y1)。此时,过n2的法线与节圆的交点为瞬心p2,过n1的法线与节圆和y轴的交点分别为瞬心p1和点8。由主、从轮廓间的共轭关系[6],得∠p2o17= ∠p1o16= θ;∠8p1o1=∠n2p2o1=α(θ)为θ位置下的瞬心传动角(简称为瞬角);n2p2=n1p1=ρ(θ)为θ位置下的瞬心半径(简称为瞬径)。
在图1所示的xo1y坐标系下,以θ∈[0,φ]为瞬变量,由o1p2、n2p2与-y轴(或叶轴)间的夹角分别为2φ-θ和π-α-(2φ-θ),得n2,n1的坐标,即节圆内、外工作轮廓的统一坐标方程为:

式中,dy1/dx1、dρ/dθ、dα /dθ为y1对x1,ρ对θ,α对θ的一阶导数,均由工作轮廓的定义确定。
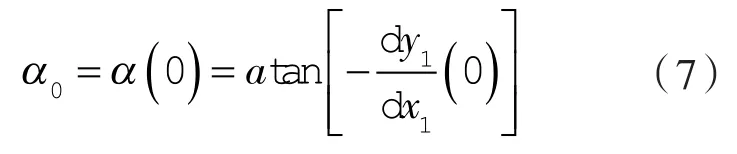
2 工作轮廓的极限条件
设n1,n2处的曲径为ρ1(θ),ρ2(θ),如ρ2(θ)<0,则会出现“角点”一类的的几何干涉[6-8]。故,ρ2(θ)≥0并取得极小值为极限状态,对应的θ=θ*,ρ2(θ*)=min[ρ2(θ)]≥ 0。记n1(ρ2(θ*)>0)、n2((ρ2(θ*)>0)为顶、谷工作极限点;n1(ρ2(θ*)=0)、n2(ρ2(θ*)=0)为顶、谷的 0 工作极限点。
根据n1,n2共轭上的欧拉 - 萨伐里方程[10],由
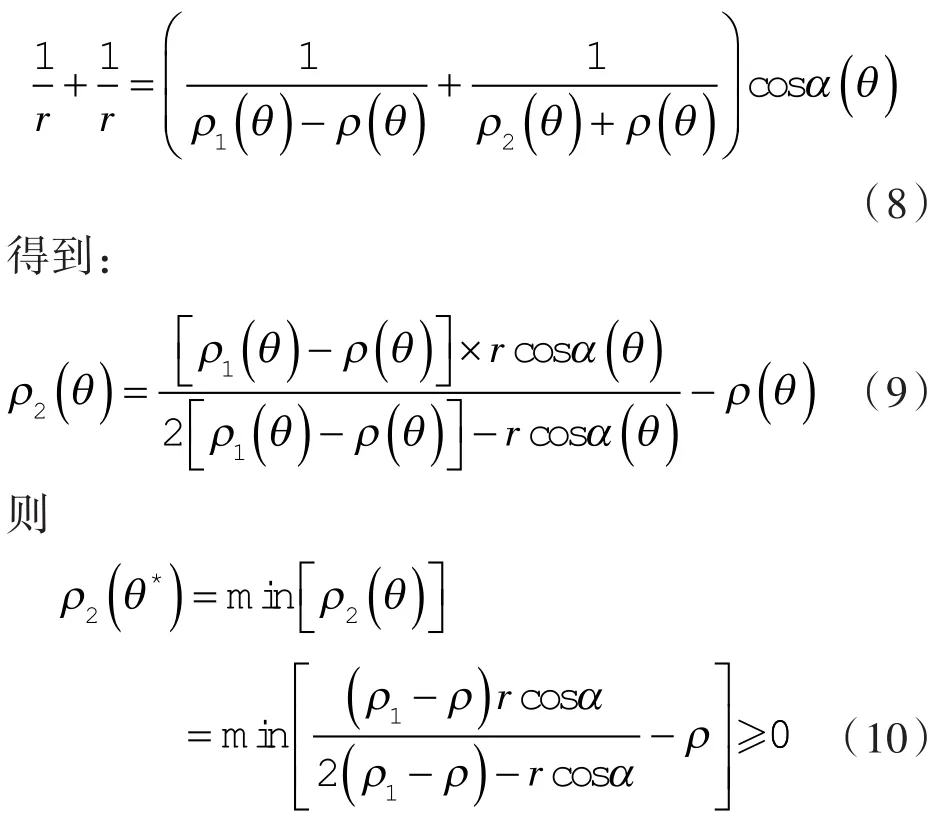
第1 种情况:ρ1(θ*)≠∞,ρ2(θ*)≠∞。例如渐开线、圆弧、摆线、抛物线等工作轮廓。由式(10)可得到:
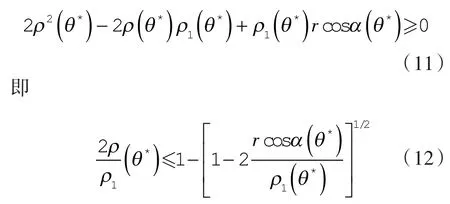
则,第1种情况的极限条件为:
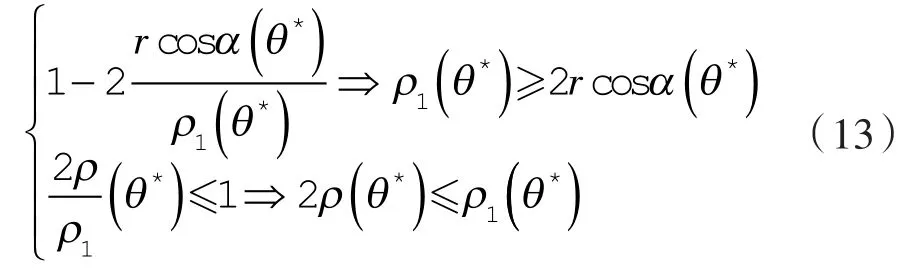
式中,ρ2(θ*)=0,取“=”号。
第2种情况:ρ1(θ)=∞的直线段,例如斜顶线工作轮廓,则由式(8)得出:

得第2种情况的极限条件为:
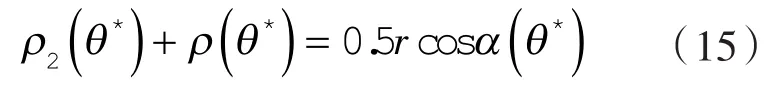
第3种情况:ρ2(θ)=∞的直线段,例如直谷线工作轮廓,则由式(8)得出:
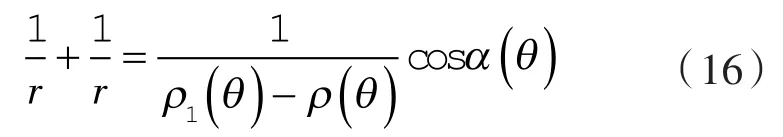
得第3种情况的极限条件为:

3 第1种情况的上限验证
以渐开线转子为例,轮廓如图2所示。此时,由渐开线轮廓成形原理可知[11]:
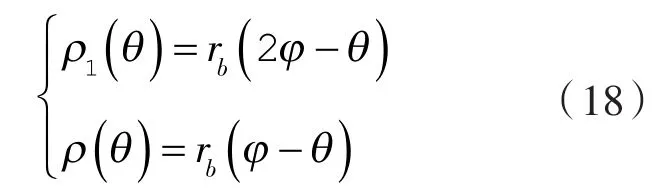
式中,rb=rsinα为基圆半径,如图2所示。将式(18)代入式(13),得:
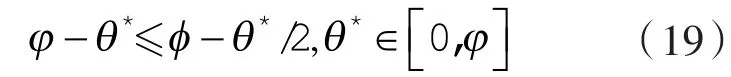
显然,θ*=0,ρ2(θ*)=0,ρ1(θ*)取得极大值,n2(θ*),n1(θ*)位于轮廓,的起始端点2,4处。
则:
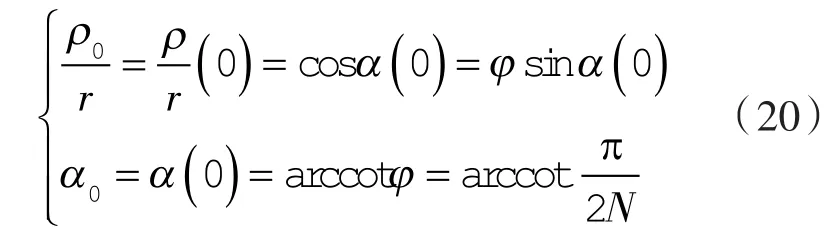
上限形状系数ε*为:

与文献[7,11]结果完全一致。
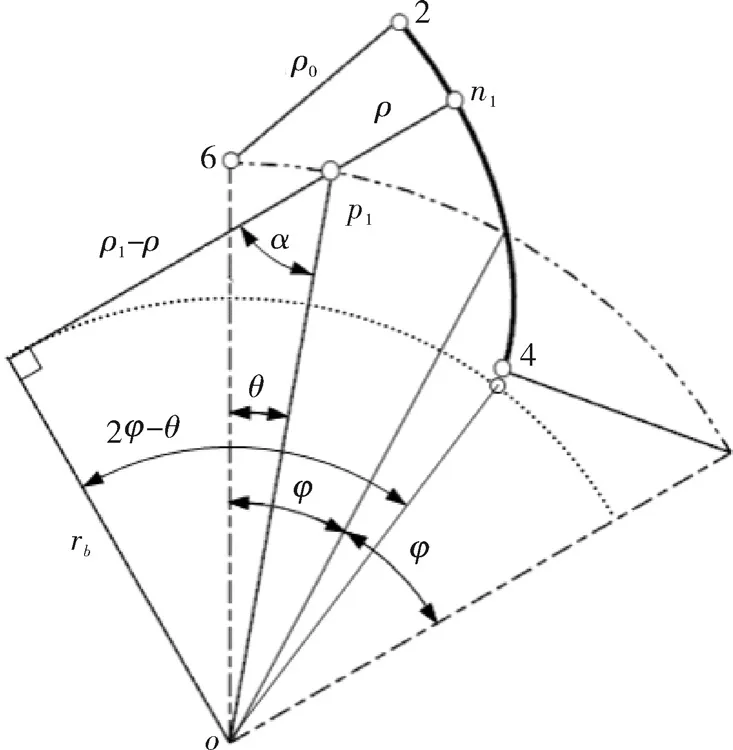
图2 渐开线转子轮廓
4 第2种情况的上限验证
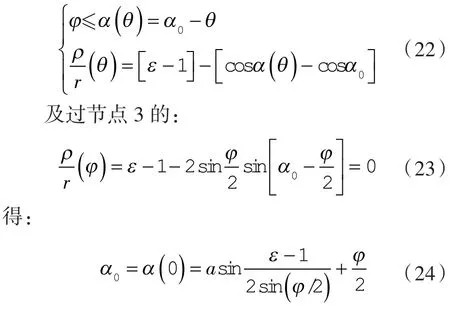
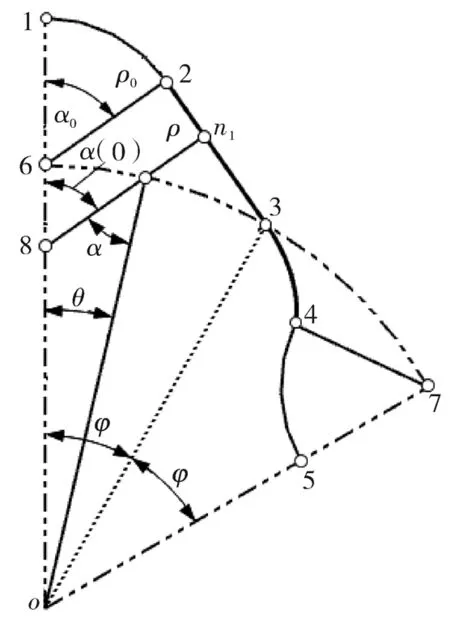
图3 顶斜线转子轮廓
由式(15)得出:
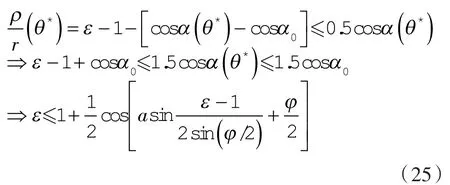
显然,θ*=0,ρ2(θ*)取得不等于零的极小值;n2(θ*),n1(θ*)位于工作轮廓各自的起始端点 2和4处,抛物线转子也存在这种现象[12-13]。得:
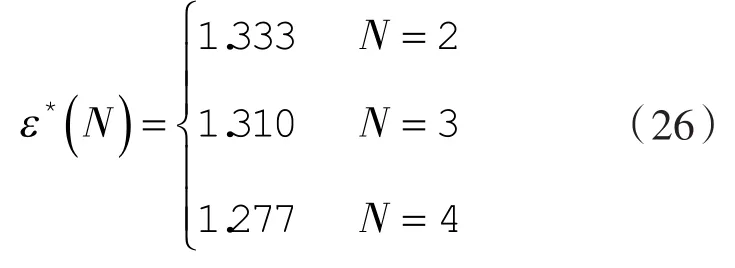
5 第3种情况的上限验证
以直谷线转子为例,轮廓如图4所示。此时,由
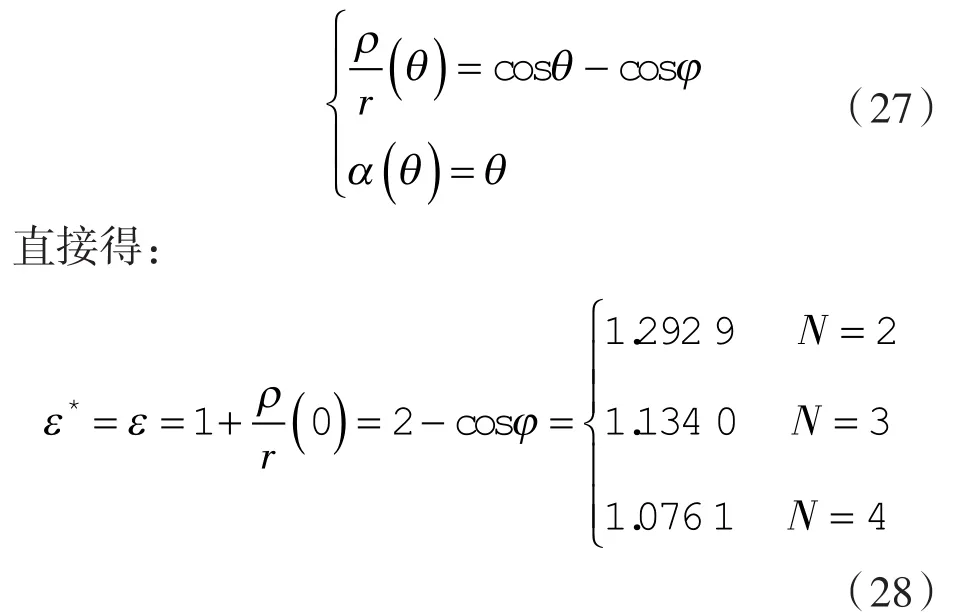
与文献[9]完全一致,因是定值,则无需考虑极限。

图4 直谷线转子轮廓
6 0工作极限状态的统一特征
当处于0工作极限状态时,表示谷工作轮廓上存在最小曲率半径为0的点。此时,由式(13)可得:
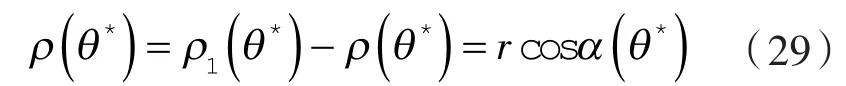
在△o8p1中,由
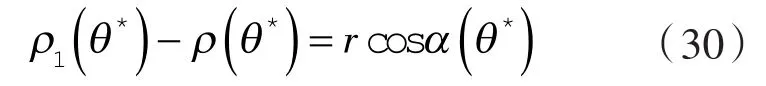
知,∠o8p1=π/2。
结合式(29)、(30)和图2,得0工作极限状态的统一特征:顶工作极限点处的曲径被其瞬心平分,且垂直于其曲心与轮心的连线[8]。
据此,谷工作极限点与轮心的连线垂直于该点法线,由此也知,渐开线、圆弧能取得0工作极限状态,顶斜线等则不能。
7 结论
(1)由谷工作极限点的轮廓特征和共轭关系上的欧拉-萨伐里方程,直接推算出转子上限形状系数,避免曲径常规计算上求解一、二导数的复杂性。
(2)谷工作轮廓存在0工作极限点时,顶工作极限点处的曲径被瞬心平分,曲径线垂直于曲心与轮心的连线;谷0工作极限点与轮心连线垂直于该点法线。
(3)谷工作轮廓不存在0工作极限点时,谷、顶工作极限点分别位于谷、顶工作轮廓的起始端点;谷工作极限点与轮心连线不垂直于该点法线。
(4)渐开线、圆弧、斜顶线、直谷线转子轮廓的极限验证,说明由极限条件推算出的上限形状系数模型正确。
