应用动能定理进行多自由度系统建模探析

薛艳霞, 苏振超

(厦门大学嘉庚学院 土木工程学院， 福建 漳州 363105)

0 引言

众所周知, 动力学问题可以利用各种方法进行求解, 例如动量定理、 动量矩定理、 平面运动微分方程、 定轴转动微分方程、 动能定理、 功率方程、 机械能守恒定律、 达朗贝尔原理、 动力学普遍方程、 拉格朗日方程、 哈密尔顿原理等。 不同方法从不同方面反映和刻画了物体的运动规律, 有各自的使用范围。 动能定理是按照能量的观点, 将动能与力的功之间建立起关系, 从而可以利用微分形式或积分形式的动能定理建立其动力学方程。 对于单自由度系统而言, 该方程就可以描述系统的动力学行为。 而对于多自由度系统, 一般理论力学或工程力学教材[1-6]均认为虽然可以应用动能定理, 但必须与其他定理联合才能建立系统的动力学方程组。 而单独应用动能定理建立多自由度系统动力学方程的情况还很少见。 笔者发现将系统的动能用广义坐标来表示后, 将其微分并令表示为广义速度的组合, 最后令每一个广义速度前的系数项为零, 也可以得到多自由度系统的运动微分方程(本文将这种方法称为 “多自由度系统微分形式动能定理法”)。 在文[7]中也提供了应用类似方法建立系统动力学方程, 例如其中的3-38、 3-39、 3-40 等多个例题为多自由度问题, 整个求解过程相对简单, 步骤统一, 相比其他方法具有一定的优越性。 但这种方法的理论依据是什么? 据笔者检索, 未发现国内外流行的理论力学或工程力学教材对此进行论述, 未见提及这种建立系统动力学方程的依据。

本文拟对动能定理应用于多自由度系统的问题展开讨论, 首先给出动能定理应用于多自由度系统的定理, 然后给出其反例, 以提示使用这种方法的局限性。 需要说明的是, 由于文[7]中的方法是先利用动能定理的积分形式, 然后再对时间求导数, 故本文为节省篇幅, 直接使用动能定理的微分形式进行讨论。

1 可独立用动能定理完成建模的一类多自由度系统

定理1 对于受到双面定常完整理想约束的多自由度系统, 如果系统动能的表达式中不显含广义坐标, 则令微分形式动能定理的广义坐标展开式中各广义坐标微分的系数项为零, 即可得到系统的动力学方程。

证 假设多自由度系统的质点数为n, 自由度数为k, 受到双面定常完整约束。 若选其广义坐标为： q1, q2, …, qk, 则各质点的位置ri可表示为：

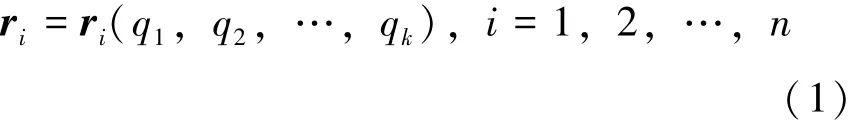
因而系统中各质点的速度˙ri及系统动能T 可表示为：

由于mij= mji, 故式(6)中dqj前面的系数与用拉格朗日方程求得的式(5)中的左端一致。 即在定理1 的条件下, 利用动能定理的微分形式求得的多自由度系统的动力学方程与用拉格朗日方程求得的动力学方程完全一致, 因此可用来求解这种特殊情况下系统的动力学方程。

对于单自由度系统而言, 质点的动能自然不包含位置坐标, 由定理1 可知结果必然正确, 这也是理论力学中一般采用的情况。

定理1 表明微分形式的动能定理可以用来处理一类特殊的多自由度系统, 从而在一定程度上扩大了动能定理的适用范围, 扩展了人们对微分形式动能定理的认识, 具体示例不再介绍。 但需要注意的是, 直接令动能定理的微分和式中各广义坐标的微分前系数为零在物理上并不是因为各广义坐标的微分相互独立。 事实上, 各广义坐标的微分(即微小实位移) 是不独立的, 它们之间存在着一定的联系[8], 只是对于满足定理1 条件的系统, 动能定理的微分形式中广义坐标微分前的系数项刚好与拉格朗日方程的虚位移前的系数项一致, 才使得微分形式动能定理具有这样的适用性。

而对于不满足定理1 条件的系统, 则无法保证动能定理的微分形式中广义坐标微分前的系数刚好与拉格朗日方程虚位移前的系数一致, 因此也就无法直接令其为零而得到正确的系统动力学方程。 现举例进行比较说明。

2 举例及讨论

文[7]中的例题3-38、 3-39、 3-40 等, 其中的动能表达式中不仅包含广义速度项, 而且显含广义坐标, 故上述定理1 不适用。 对于这类问题的求解, 多自由度系统微分形式动能定理法是否也适用呢? 在此给出一个类似的例子, 并加以讨论。

例1 已知位于铅垂平面的图1 所示系统中, 杆件OA 和AB 长度分别为2l1和2l2、 质量分别为m1和m2, 用光滑铰链连接。 试建立系统的运动微分方程。

解 该系统约束显然为双面完整定常的理想约束。 以两杆的转角θ 和φ 为广义坐标。 由于：

则系统的动能为：

图1 例1 示意图

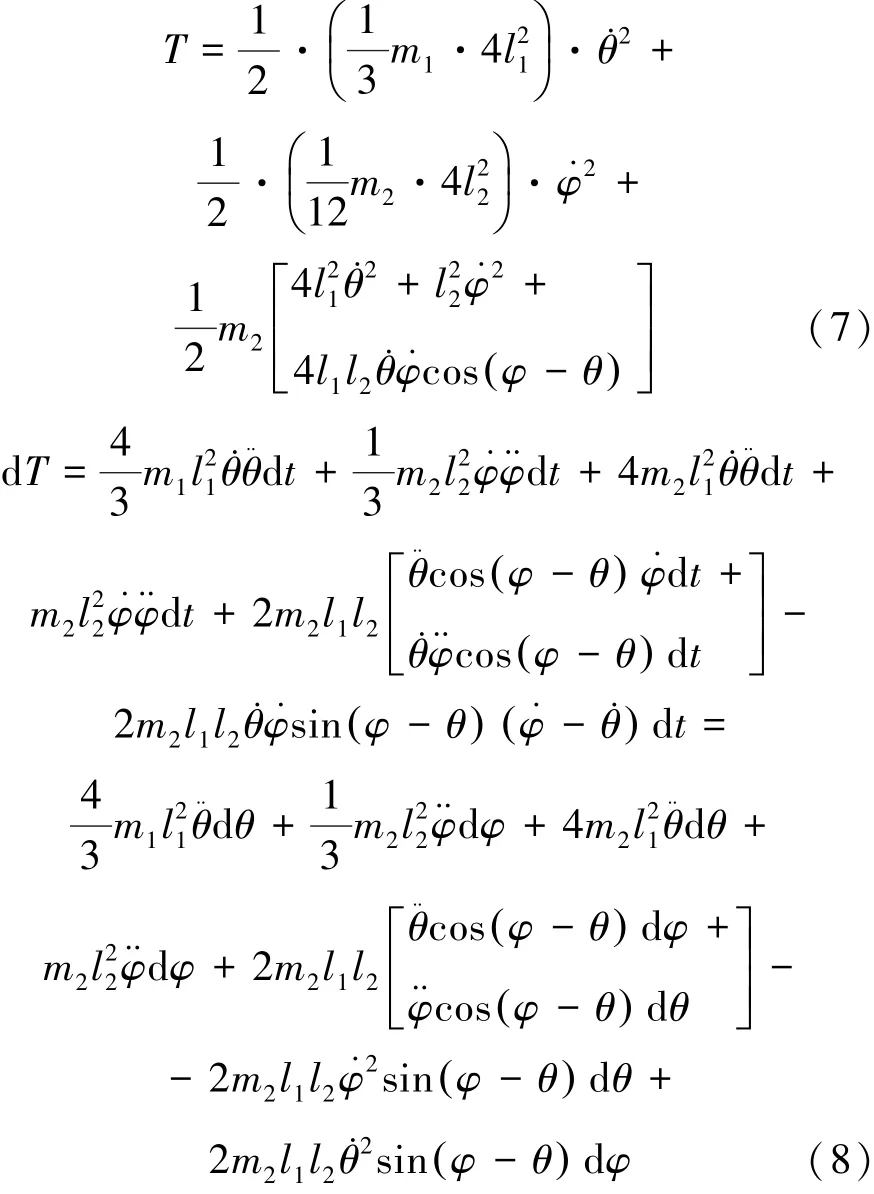
式(8)中, 在归类时采用将2m2l1l2˙θ˙φsin(φ - θ) ˙φdt项归结为2m2l1l2˙φ2sin((φ - θ)dθ , 2m2l1l2˙θ˙φsin(φ- θ)˙θdt 项归结为2m2l1l2˙θ2sin(φ - θ)dφ 等。 而外力的元功之和为：

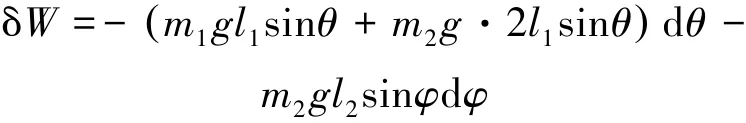
由于dT = δW , 可得：

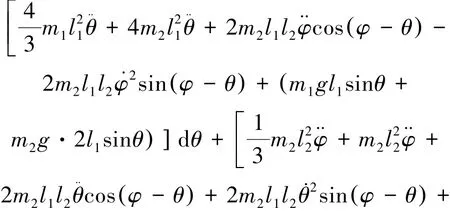
利用多自由度系统微分形式动能定理法, 则该系统的动力学方程为：

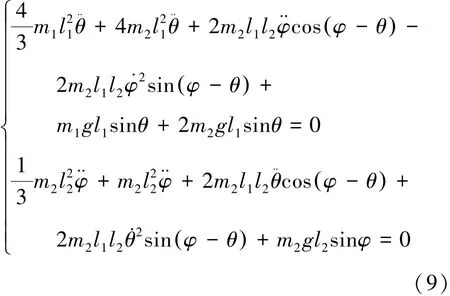
经验证方程(9)与由拉格朗日方程所得结果完全相同。

但若将式(8)中2m2l1l2θ˙φ˙sin ( φ - θ) φ˙dt 项归2m2l1l2θ˙φ˙sin ( φ - θ) θ˙dt 项 归 结 为2m2l1l2θ˙φ˙sin ( φ - θ) dθ 。 则类似可得方程为：

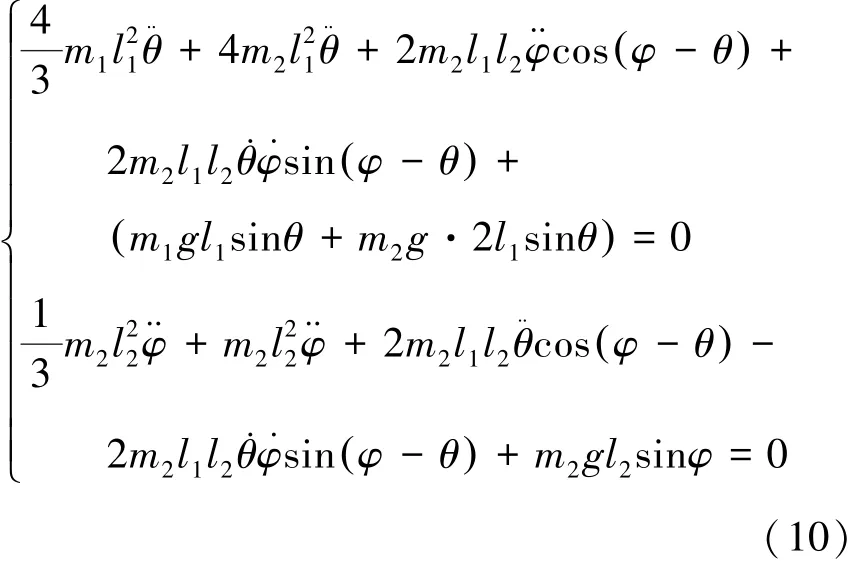
由拉格朗日方程可以证明这样得到的方程(10)是错误的。

在本例的计算过程中, 动能函数为广义坐标的二次齐次函数, 但部分系数中显含有广义坐标, 所以并不满足定理1 的条件。 对于这类问题,在应用时需要特别留意2m2l1l2˙θ˙φsin (φ - θ) ˙φdt 应该 等 于2m2l1l2˙φ2sin (φ - θ) dθ , 而 不 能 等 于2m2l1l2˙θ˙φsin (φ - θ) dφ 。

由此可以看出, 对于不满足定理1 条件的系统使用定理1, 虽有可能得到正确结果, 但存在很大的不确定性, 即存在二义性问题, 而对于自由度大于2 的系统, 则可能出现多义性问题。 上述多义性问题在文[7] 的3-38、 3-39、 3-40 等例题中也一样存在, 只是作者明智地选择了第一种方式归结, 而没有采用其他归结方式。 这说明定理1 的条件是有用的。

如何消除上面所说的多义性? 笔者发现在导数与微分之间归结时应遵循以下规律： 不同速度乘积项归结后的结果中某广义坐标的线性速度项与其微分项不应在同一个表达式中。 例如, 例1 的计 算 过 程 中 ˙θ˙φsin (φ - θ) ˙φdt 项 应 归 结 为˙φ2sin (φ - θ) dθ , 而 不 能 归 结 为˙φ˙θsin (φ - θ) dφ 。

如果说对于例1 多自由度系统微分形式动能定理法经改良还可以使用的话, 那么对于下面的例2, 独立应用动能定理则根本无法得到正确的结果。

例2 图2 所示系统中, 均质杆的质量为m1, 在铅垂平面Oxy 内运动, 质量为m2的滑块可以在杆上无摩擦地滑动, 若外力偶矩为Tθ,物块与转轴的距离为ρ , 杆的转角为θ , 试建立该系统的动力学方程。

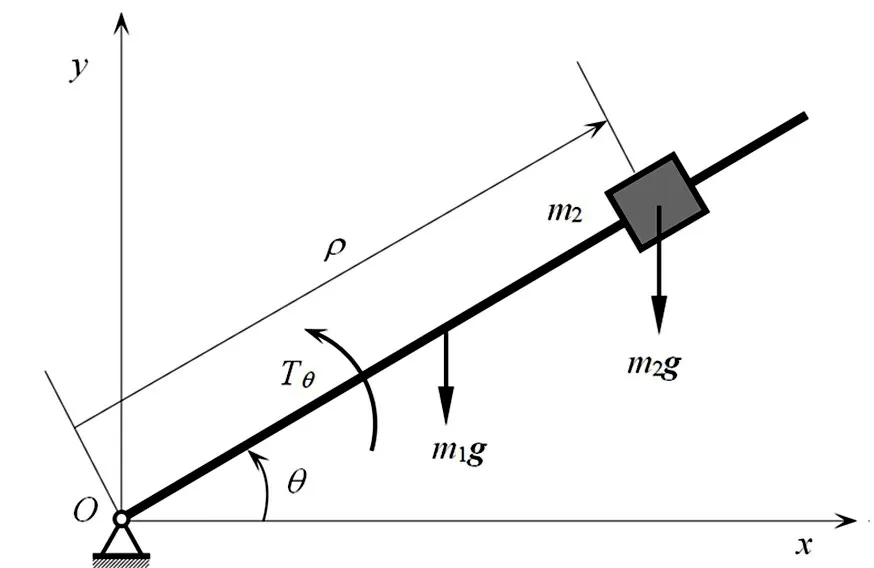
图2 例2 示意图

解 该系统约束显然为双面完整定常的理想约束。 选择系统广义坐标为q1= ρ 、 q2= θ , 则此时系统的动能可表示为：

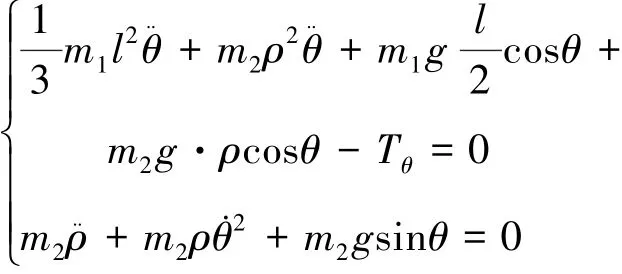
按照多自由度系统微分形式动能定理法, 则可得系统的动力学方程为：

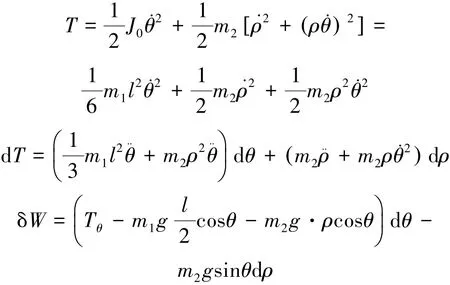
经分析, 上述结果与基于拉格朗日方程所得结果[9]不同。 所以对于这类动能表达式中显含广义坐标的系统, 多自由度系统微分形式动能定理法不再适用, 且对于本例无论如何改良均不能得到正确解。 产生这种问题的原因本质上说是因为广义坐标的微分表示的是系统的实位移, 它们之间有密切的联系, 微分形式动能定理的关于广义坐标微分的和式中, 广义坐标微分前的系数项没有将系统动力学方程解耦。 自然, 按照多自由度系统微分形式动能定理法无法得到正确的解。

3 结论

本文针对一种独立应用动能定理建立多自由度系统动力学方程的方法, 探讨这种方法的理论依据, 给出了独立应用动能定理而获得多自由度系统全部动力学方程的适用性及使用条件, 证明了对于动能表达式中不显含广义坐标的系统, 独立使用微分形式动能定理也可得到与拉格朗日方程完全相同的结果。 该结论扩大了动能定理的应用范围, 有利于对动能定理相关内容的深化, 在没有应用拉格朗日方程的情况下, 对满足定理1条件的系统, 可以单独应用动能定理的微分形式快速建立其动力学方程, 为求解这一类相关问题带来很大方便。 同时强调对于不满足定理1 条件的系统, 使用多自由度系统微分形式动能定理法建模时会存在二义性甚至多义性问题, 在建立方程时需要注意其归结方式； 而对于有些问题, 例如本文中的例题2, 应用多自由度系统微分形式动能定理法则根本无法获得正确结论, 说明使用该方法有比较严格的条件。

致谢： 本文写作过程中, 南京航空航天大学王怀磊博士曾与本文通讯作者多次讨论并提供建设性建议,在此表示感谢。