广义Fibonacci 多项式的矩阵表示及Hadamard 积

陈庆华, 杨标桂

( 福建师范大学 数学与信息学院， 福建 福州 350108 )

0 引言

Fibonacci 数列最初是由兔子繁殖问题得到的二阶递推关系的数列, 若数列 { Fn} 是Fibonacci数列, 那么就可以得出结论： F0= 0,F1= 1, Fn= Fn-1+ Fn-2(n ≥2, n ∈N) 。

很多学者都对Fibonacci 数列进行了相关的研究, 将其推广为Lucas 数、 Pell 数、 Jacobsthal数等, 研究它们的通项公式、 生成函数, 并推广到各式各样的多项式序列, 如Fibonacci 多项式、Lucas 多项式等, 且取得了许多成果。 文[1] 定义了(p, q)-Fibonacci 多项式及un(x) 和(p, q)-Lucas 多项式vn(x) , 作为Fibonacci 多项式和Lucas 多项式的推广。 此外, 有许多学者研究一些特殊数列的矩阵表示, 其中： Silvester 在文[2]中首次给出Fibonacci 数列的矩阵表示形式QL-矩阵； 类似的, 在文[3]中, 定义了Lucas 数列的矩阵表示形式； 此外, 文[4-7]探讨了相关数列的矩阵表示及其若干性质。 在文[8]中, 作者在定义bi-periodic Fibonacci 和bi-periodic Lucas数列的矩阵表示形式基础上, 又得出它们的Hadamard积以及一些性质。

1 预备知识

在文[ 1] 中, ( p, q)-Fibonacci 多项式un(x) 被定义为：

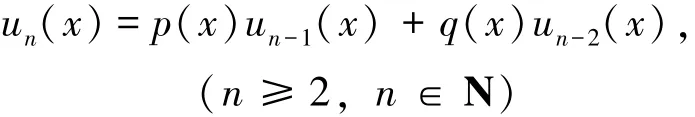
且有u0(x) = 0, u1(x) = 1, u2(x) = p 。

为简洁起见, 在下文的证明公式中, 将多项式p(x) 简写成p , q(x) 简写成q , un(x) 简写成un。

令α 和β 为特征方程t2- p(x)t - q(x)= 0 的根, 则

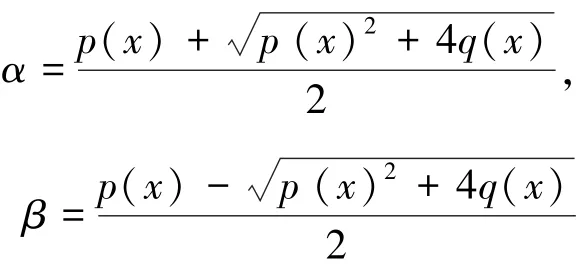
且α + β = p(x), αβ =- q(x) 。 由特征根α 和β, 可以得出序列(un( x)) 满足Binet 公式

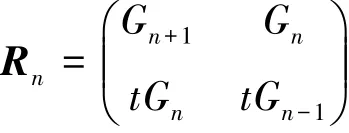
在这里具体给出了广义数列的矩阵表示方法, 为相关论文的研究奠定了基础。

已知两个矩阵A = (aij)m×n, B = (bij)m×n的Hadamard 积定义为

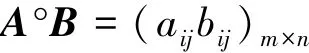
且文[10]中定义了关于Fibonacci 矩阵与它的逆矩阵的Hadamard 积：

上面的结论说明矩阵和Fibonacci 数之间有着密切的联系。 基于以上研究成果, 本文得出以下结论。

2 (p，q)-Fibonacci 多项式的矩阵表示及其性质

定义1 (p, q)-Fibonacci 多项式的矩阵表示U(p,q)为

可以看到当n = 1 和n = 2 时, 式(2) 成立, 假设当n =k 时也成立, 即

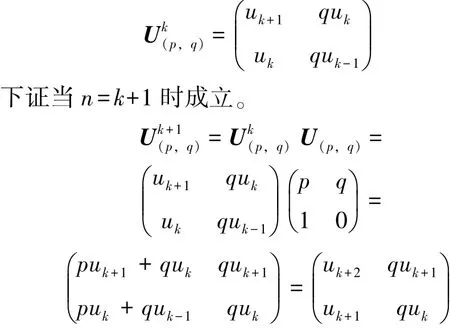
故式(2)对所有的正整数n 成立。

推论1对所有的正整数n, 有下列等式成立。

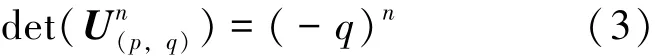
证利用数学归纳法证明, 当n = 1 时,det(U(p,q)) = ( - q) , 即式(3)成立。

假设当n = k 时成立, 即det( Uk(p,q)) =( - q)k, 则由行列式乘法的性质, 可得

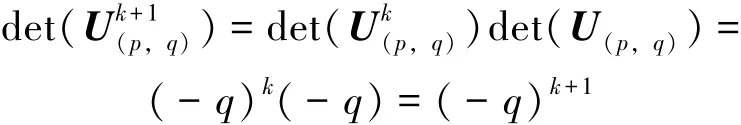
即对所有的正整数n, 有式(3) 成立。

推论2由式(2)可以得到Cassini 恒等式：

推论3对所有的正整数n , 有下列等式成立。

这里I 为单位矩阵。

证 Un(p,q)的逆矩阵为：

定理2对任意的正整数n, (p,q) -Fibonacci多项式的Binet 公式为：

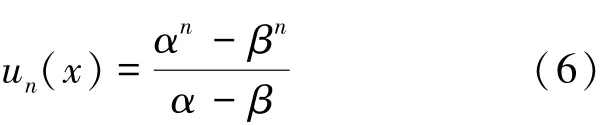
其中：

再由矩阵的性质可得U(p,q)= WVW-1, 则有。 因此可以得到：

另一方面, 比较位于第二行、 第一列的项,可以得到第二个等式, 下面证明第三个等式。

定理4对任意整数n, 有

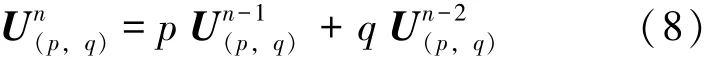
证 由式(2) 和多项式un(x) 的递推公式,可以得到：

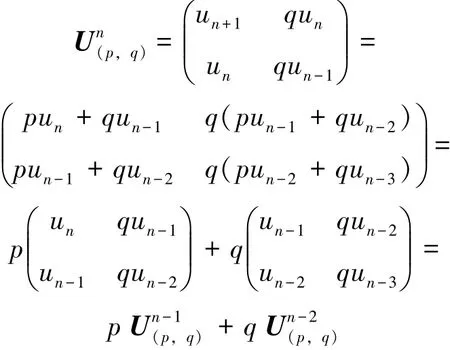
3 关于(p，q)-Fibonacci 矩阵表示形式的Hadamard 积

又由Cassini 恒等式知：

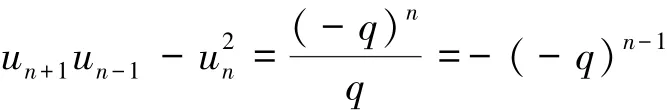
因此,