基于改进型蜻蜓算法的车辆路径问题研究
2020-12-25陶文瀚赵晨聪孙翌博刘晨磊孙知信
陶文瀚,赵晨聪,孙翌博,刘晨磊,孙知信,孙 哲
(1.南京邮电大学 现代邮政学院&现代邮政研究院,江苏 南京 210003;2.常州工学院 计算机信息工程学院,江苏 常州 213032;3.南京邮电大学 宽带无线通信与传感网技术教育部重点实验室,江苏 南京 210003)
0 引 言
车辆路径问题(vehicle routing problem,VRP)[1]是物流配送优化环节中至关重要的一环。在物流配送过程中,通过为配送车辆选择最优的运输路径,合理安排车辆的调度顺序,可以有效减少车辆的空车行驶率和行驶距离。该问题最早由国外学者Dantzig和Ramser在1959年提出,属于NP-Hard问题[2]。目前,国内外学者对VRP问题已经进行了广泛而深入的研究,VRP已经应用到垃圾车的线路优化、连锁商店的送货线路优化等[3]众多社会领域。
但是,传统的VRP问题往往只考虑到配送距离而忽视了客户对配送时间的要求,进而影响客户对物流配送服务的满意度。带时间窗约束的车辆路径问题是原车辆路径问题的一种拓展,在经典组合优化车辆路径问题上,引进了客户对货物到达时间的时间窗约束。其中,时窗约束可以分为两种,一种是硬时间窗,要求车辆必须要在时窗内到达,早到必须等待,而迟到则拒收;另一种是软时窗,不一定要在时窗内到达,但是超出时间窗到达则需要处罚。
该文总结众多新型智能算法应用到车辆路径问题上的优缺点,分析当前路径规划上存在的问题和需求,提出了一种改进型蜻蜓算法,并将该算法应用到带软时间窗约束的车辆路径问题中,发现该算法在求解VRP问题上具有较高的可行性。
1 相关研究
目前,已有许多新型智能算法用于求解带时间窗约束的车辆路径问题[4]。文献[5]通过使用禁忌搜索算法和自适应大邻域搜索算法来解决具有时间依赖性的软时间窗和随机行驶时间的车辆路径问题,并说明该方法可用于解决其他一些大规模问题。文献[6]利用人工蜂群激发蜜蜂的觅食行为,运用混合超启发式算法求解带软时间窗的多目标车辆路径问题。文献[7]提出了一种使用分布估计算法的方法,通过使用广义的Mallows分布作为概率模型来描述解空间的分布,以解决带时间窗的车辆路径问题。文献[8]探索了时变多行车辆路径问题(TDMTVRP),使用了具有改进行进速度的模型,与容量较大的VRPTW[9]相比,减少了行车时间和行进距离,并通过使用最近邻启发式算法获得初始解和禁忌搜索启发式算法搜索最优解。文献[10]提出了一种基于改进的头脑风暴优化算法(IBSO-ACO)的新型蚁群优化算法,以解决带有软时间窗的车辆路径问题。文献[11]开发了一种混合遗传算法的求解方法,对遗传算法和变量邻域搜索方法(VNS)进行了杂交,以解决带有软时间窗的静态和动态车辆路径问题。这些学者对带有时间窗的车辆路径问题进行了系统而深入的研究,但他们的研究大多使用改进型的传统启发式算法,例如遗传算法、蚁群算法和禁忌搜索算法等。这些算法在带时间窗约束VRP的求解上取得了可喜的成果,但也存在不少问题,如禁忌搜索算法对初始解的依赖性较高,遗传算法存在局部搜索能力不强、易陷入早熟、总体上可行解的质量不是很高等缺点。
蜻蜓算法(dragonfly algorithm,DA)自从2015年被Mirjalili[12]提出就得到了广泛的研究与应用。该新型算法已被成功用于医疗疾病预测诊断[13]、太阳能热系统优化[14]、小麦碰撞声信号检测与识别[15]等诸多领域。其中,Abdelaziz I. Hammouri等[16]将蜻蜓算法运用到旅行商问题(TSP)的求解之中,验证了蜻蜓算法在求解类路径规划问题的可行性。文献[17]使用DA来估计随机部署在指定区域中的节点的位置,通过仿真实验来表明DA可以为基于范围的定位产生低误差。文献[18]提出了一种用于预测问题的带有极限学习机(ELM)系统的混合蜻蜓算法,通过利用DA在隐藏层中选择较少数量的节点,以加快ELM的性能。
然而,在软时间窗的约束下,针对原蜻蜓算法解决大规模问题时存在收敛速度慢、运算时间长、容易陷入局部最优解等缺陷[19],该文提出一种改进型的蜻蜓算法应用于车辆路径问题,从而更好地提高物流运输车辆的配送效率。
2 问题描述及数学模型
带时间窗约束的车辆路径问题可以描述为:一个配送中心,拥有一定数量的同种车辆,车辆容量有限且已知,车辆满载货物由配送中心出发,向区域内若干客户配送同种商品,要求在完成配送任务的总路程最短的基础上派出的车辆数最少,并考虑在客户点的驻留成本、未在规定时间内送达的惩罚成本。
该文从实际物流车辆运输特点和自身实验条件出发,对构建的带时间窗约束的车辆路径问题数学模型进行如下假设:
(1)车辆必须从固定的配送站点出发,运输途中不经停该站点,在完成一趟运输过程之后才能回到配送站点;
(2)规定车辆以一种恒定的行驶速度在各站点之间行驶;
(3)各服务点的需求量、服务时间窗、服务时间不会临时变动;
(4)各服务点之间的路径都可达,并且不会产生任何突发事件影响车辆的行驶;
(5)一辆车只可以同时服务一个服务点、配送一条路线。
根据以上数学模型假设,对构建的带时间窗的车辆路径问题数学模型中的参数和相关的变量进行如下定义:
V={1,2,…,n}表示站点编号集合,n为站点总个数,编号1为起始站点。
Pos表示配送站点和客户服务站点的位置集合,其中(Posix,Posiy)表示站点i的横、纵坐标位置。
Dis表示各个站点之间的距离,站点i与站点j之间的距离Disij由式(1)给出。
(1)
Ser_Time为站点的服务时间集合,其中Ser_Timei表示站点i的服务时间。
Demand为站点的服务需求量集合,其中Demandi表示站点i的货物需求量。
TW表示各站点规定的服务时间窗,其中TWilast表
示站点i服务时间窗的最大非处罚服务时间。
duty记录车辆已经服务过的站点序列。
v_vel表示车辆行驶的速度。
v_cap表示车辆的最大载重量。
αij判断车辆是否经过站点i和站点j之间的路线。当αij=1时,表示车辆经过;当αij=0时,表示车辆没有经过。
βi判断站点i是否已经服务过。当βi=1时,表示站点i已经服务过;当βi=0时,表示没有服务过。
γi判断车辆在到达站点i时时间是否超出该站点的时间窗上限。当γi=1时,表示超过;当γi=0时,表示没有。
time记录车辆刚到达某一站点时的当前时间,其计算公式由式(2)给出。
(2)
ctrans、cser和cpun分别表示车辆单位行驶路程、单位服务时间和单位惩罚时间成本。
综上所述,该文构建的数学模型目标函数由式(3)给出。
Ser_Timei-TWilast)*cpun
(3)
约束条件如下所示。
(4)
(5)
(6)
0≤d_n≤n
(7)
(8)
(9)
3 模型实现
3.1 蜻蜓算法概述
蜻蜓算法是受蜻蜓行为启发而提出的一种新型群智能算法。与其他的群智能优化算法类似的是,蜻蜓算法也有着较好的局部最优解避免能力和精确近似全局最优解的能力。
蜻蜓算法像大多数群智能算法一样皆是遵循“求生”的原则,蜻蜓个体有两个行为:寻找食物和躲避天敌,蜻蜓群体的位置移动由以下五种行为组成:
(1)分离,即蜻蜓与相邻个体之间避免碰撞。
式中,X是当前个体的位置;Xj是第j个附近个体的位置;N是附近个体的个数。
(2)结队,即相邻个体之间倾向于保持相同的速度。
式中,Vj是第j个附近个体的速度。
(3)聚集,即蜻蜓倾向于向相邻个体中心聚集。
(4)觅食,即蜻蜓对食物的倾向度。
Fi=X+-X
式中,X+是蜻蜓食物的位置。
(5)躲避天敌,即蜻蜓避免被天敌捕食,对其产生排斥。
Ei=X-+X
式中,X-是蜻蜓天敌的位置。
除以上五种行为之外,为了较为准确地模拟出蜻蜓的移动过程,Mirjalili又引入了两个量:步长向量(dX)和位置向量X。步长向量计算公式如下(这是逐维定义的步长):
ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔXt
式中,s表示分离权重,a表示结队权重,c表示聚集权重,f表示食物因子,e表示天敌因子;Si表示第i个体分离之后的位置,Ai表示第i个体结队之后的位置,Ci表示第i个体聚集之后的位置,Fi表示第i个体蜻蜓食物的位置,Ei表示第i个体蜻蜓天敌的位置;w表示惯性权重;t表示当前迭代次数。
位置更新如下:
(6)附近存在蜻蜓个体,则按照如下方式更新:
Xt+1=Xt+ΔXt+1
(7)附近不存在蜻蜓个体,则执行莱维飞行:
Xt+1=Xt+Levy(d)×Xt
式中,d是求解问题的维数。
3.2 改进型蜻蜓算法
通过研究发现,采用传统蜻蜓算法求解带时间窗的车辆路径问题时,存在收敛精度较低、最优解容易陷入局部收敛等缺陷。因此,为了针对求解带时间窗的车辆路径问题,该文根据以上设计的数学模型,将随机学习优化[20]的思想融入到蜻蜓算法中,重新设计了一种能够更有效应用于带时间窗约束的车辆路径问题研究的改进型蜻蜓算法。
该算法的主要改进点在于将传统蜻蜓算法结队、觅食、避敌、避撞、聚集五种行为的实值计算形式,修改为随机学习目标位置对,即利用随机学习优化方法完成以上行为的实现:
(1)通过向同期蜻蜓种群中位置最优的蜻蜓随机学习一组排序,更新位置序列,优化局部最优解,实现结队行为;
(2)向历史蜻蜓种群中位置最优的蜻蜓随机学习一组排序,优化位置序列,趋向于全局最优解,实现觅食行为;
(3)通过远离同期蜻蜓种群中位置最差的蜻蜓位置,避免陷入局部最优,实现避敌行为;
(4)发生碰撞时,随机长度随机打乱一只蜻蜓位置,保证种群多样性,实现避撞行为。
该算法的具体实现步骤如下:
步骤1:初始化蜻蜓算法和数学模型的相关参数。其中,每一只蜻蜓的位置向量表示一种选路方式,即为除编号1外的n-1个站点编号的随机排列组合;
步骤2:计算初代各解,即站点间的距离矩阵、每只蜻蜓位置向量所对应的成本值、初代最优解和最优成本值等;
步骤3:开始迭代计数,令迭代标识符iter=1;
步骤4:通过结队、觅食、避敌、避撞等行为,进行随机学习优化排序,优化各蜻蜓的位置向量;
步骤5:利用目标函数计算每只蜻蜓位置向量所对应的运输成本值,并且记录最优值和最优蜻蜓位置向量,即记录最佳的成本值和对应的车辆路径规划方案;
步骤6:将本代最优值和历史最优值进行比较,筛选得出最优成本值和最优蜻蜓位置向量;
步骤7:迭代标识符加1;
步骤8:判断是否达到最大的迭代次数。若是,进入步骤9;若否,返回步骤4;
步骤9:得出实验结果,生成实验图表,结束。
3.3 基于改进蜻蜓算法的模型实现
基于改进型蜻蜓算法的带时间窗约束的车辆路径问题模型实现流程如图1所示。
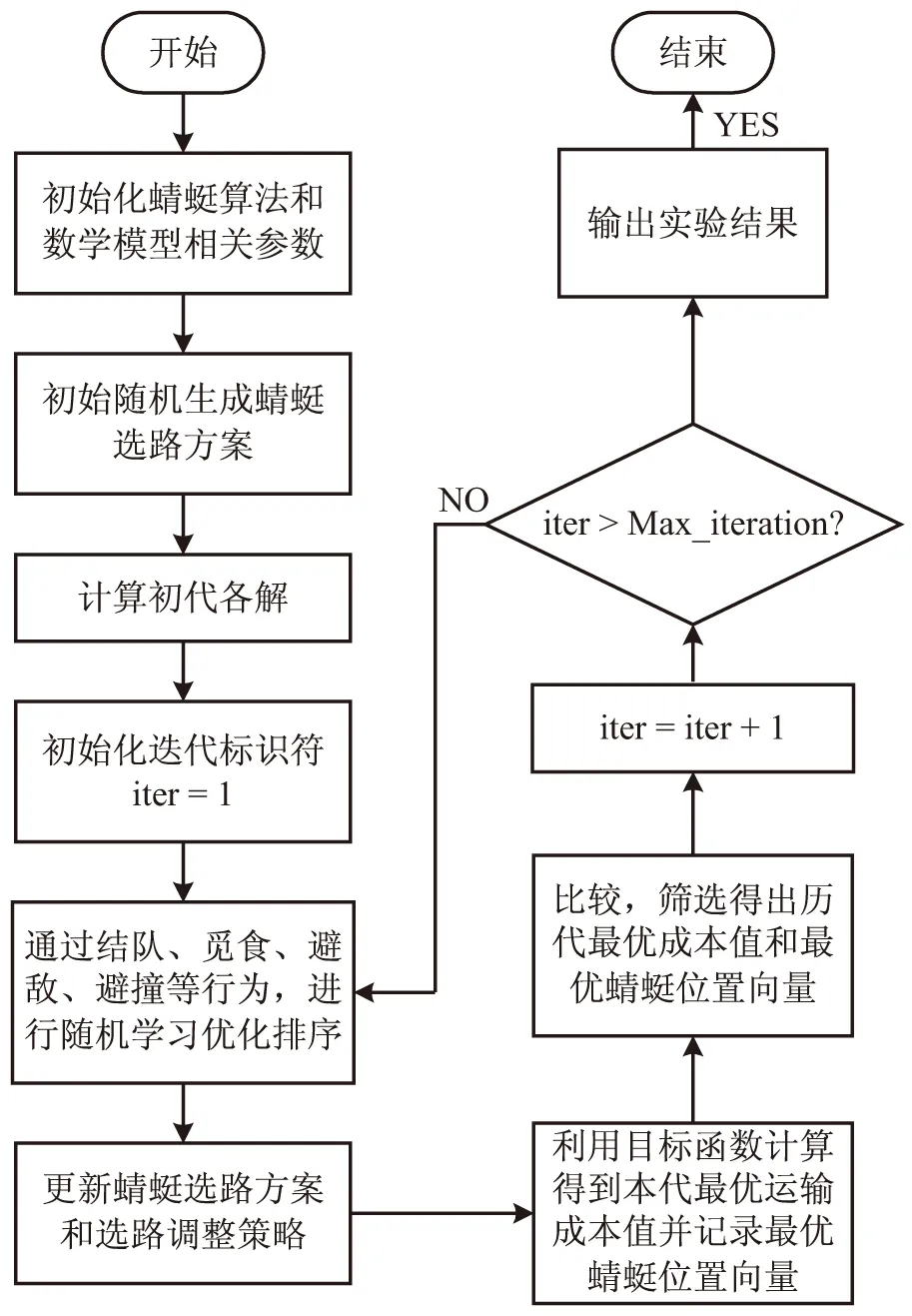
图1 改进型蜻蜓算法实现流程
4 算例实验
4.1 实验参数设置
服务站点初始参数设置如表1所示。
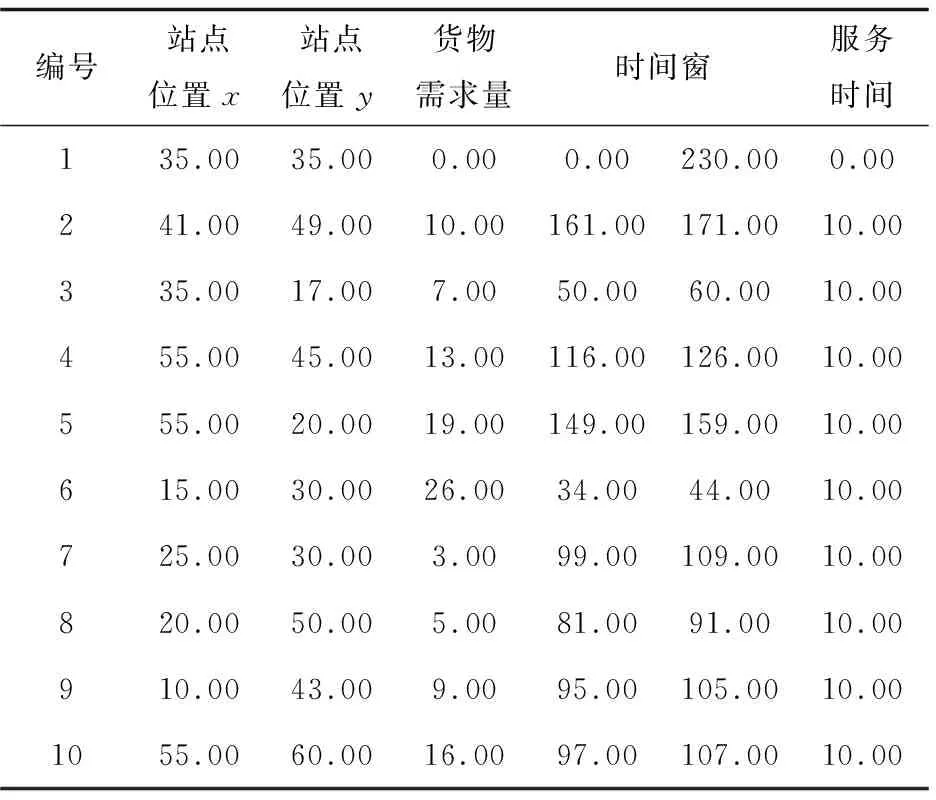
表1 服务站点参数设置
车辆初始参数设置如表2所示。

表2 车辆参数设置
改进蜻蜓算法的初始参数设置如表3所示。
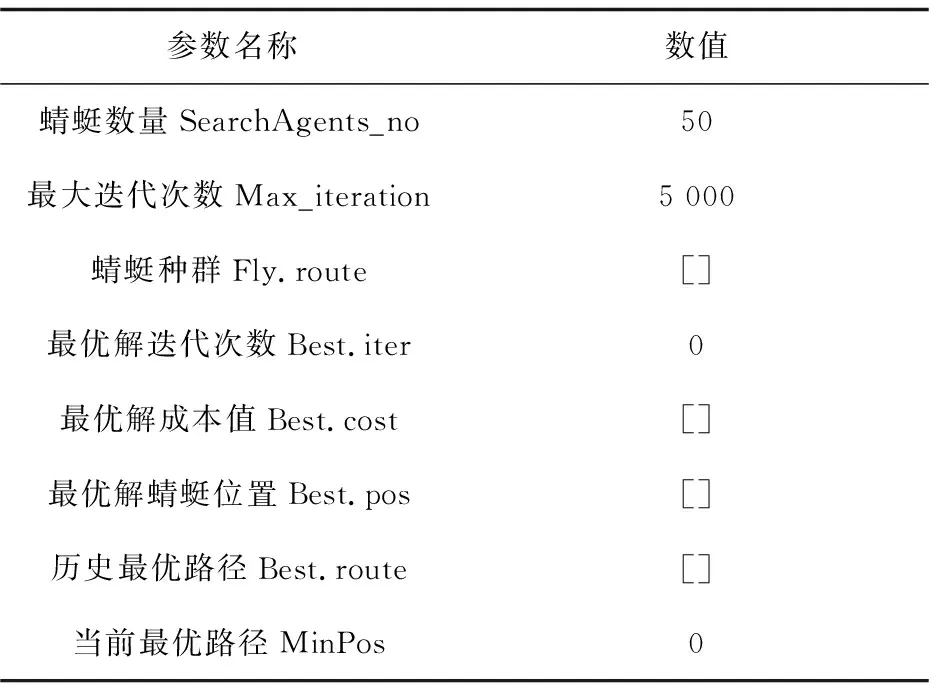
表3 蜻蜓算法参数设置
实验设计的拓扑网络环境如图2所示。

图2 实验物流网络拓扑
根据该文设计的带时间窗车辆路径问题数学模型约束条件,该物流拓扑网络一共拥有3 628 800种车辆路径规划方案。
4.2 实验结果
针对文中的车辆路径问题所提出的数学模型,将遗传算法(GA)、禁忌搜索算法(TSA)、传统蜻蜓算法(DA)和改进后的蜻蜓算法(RDA)一同进行实验测试并进行比较。为保证实验的公平性和客观性,将以上四种算法的迭代次数设为1 000次,采用相同的成本函数进行运算,得到的算法对比结果如图3所示。
由实验结果可以看出,无论是在求解精度还是收敛速度上,改进型蜻蜓算法都展现出优越的性能,充分说明改进型蜻蜓算法在求解车辆路径问题时具有更加稳定的性能。
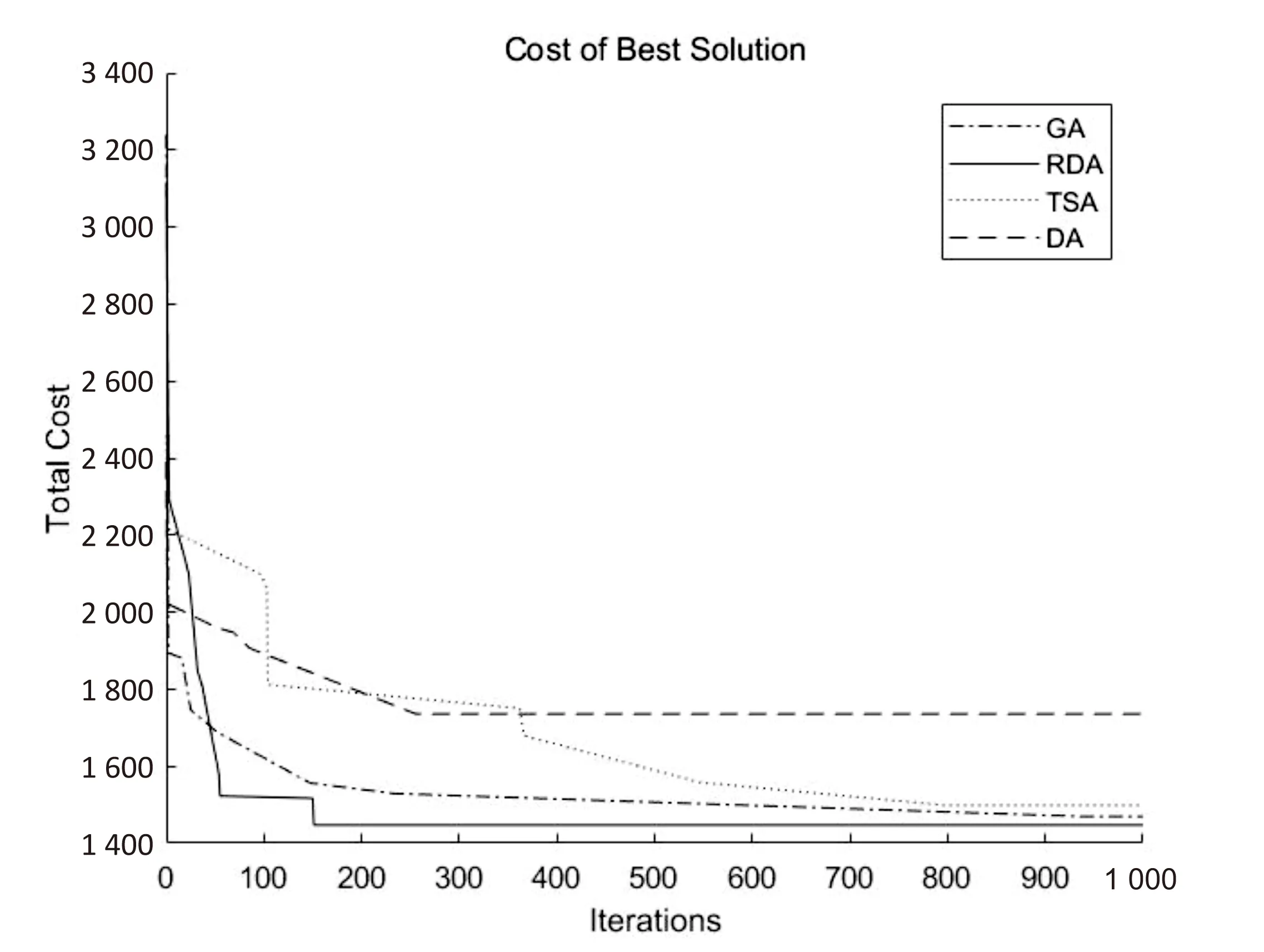
图3 算法对比
经过实验得到最优的综合成本为1 447.23。其对应的车辆路径规划方案如图4所示。
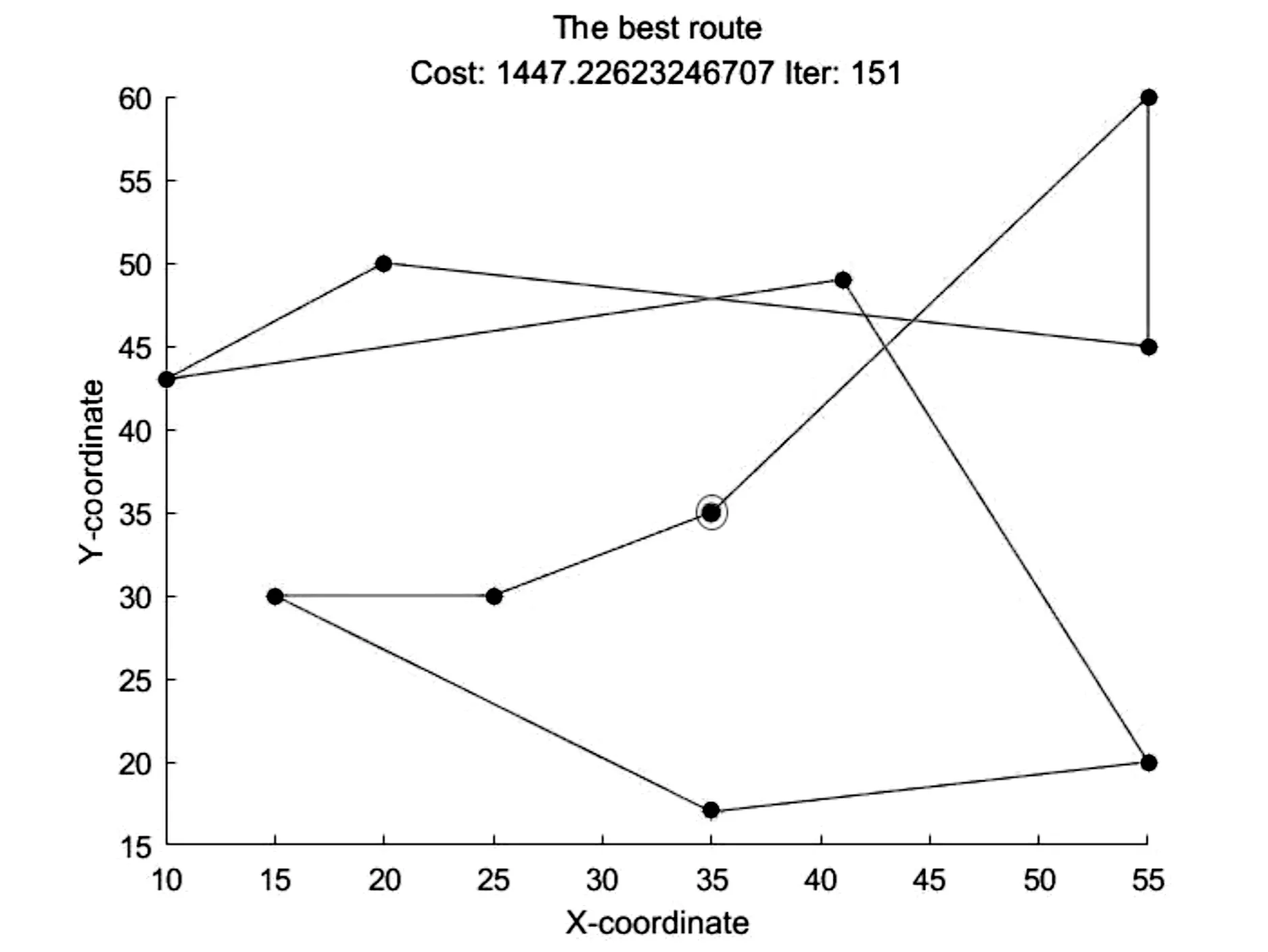
图4 最优路线规划
路线规划方案为1→7→6→3→5→2→9→8→4→10。其中,加圈位置为站点1,即始发站点。
5 结束语
讨论了带软时间窗约束的车辆路径问题,构建了一种更符合配送中心与顾客服务目标优化的带时间窗约束的车辆路径问题数学模型。通过设将随机学习优化的思想融入到原先的蜻蜓算法之中,针对车辆路径问题数学模型的求解,重新设计了一种能够更有效应用于该问题求解的改进型蜻蜓算法。
该算法的主要改进之处为:将传统的蜻蜓算法结队、觅食、避敌、避撞、聚集五种行为原则从原先的实值计算形式修改成为随机学习目标位置对,即利用随机学习优化方法完成以上行为的实现,使改进型蜻蜓算法更符合解的特性,从而得到一个更优的结果。
通过Matlab仿真实验证明了将蜻蜓算法应用到带软时间窗约束的车辆路径问题求解的可行性,并且验证了改进型蜻蜓算法用于该数学模型实现的有效性。下一步将在该研究的基础上,提高算法收敛速度和收敛精度,改进蜻蜓随机学习的优化方式,并将该算法应用于其他领域的优化。
