基于模拟退火思想的改进人工蜂群算法
2020-12-24张业清李婧芳胡鹏伟
张业清 李婧芳 胡鹏伟
摘 要： 针对人工蜂群算法（ABC）容易陷入局部极值点、进化后期收敛慢和优化精度较差等缺点。把模拟退火技术（SA）引入到ABC算法中，提出了一种改进的优化算法。混合优化算法在各温度下依次进行ABC和SA搜索，是一种两层的串行结构。由于ABC提供了并行搜索结构，所以，混合优化算法使SA转化成并行SA算法。SA的概率突跳性保证了种群的多样性，从而防止ABC算法陷入局部极小。基于模拟退火的改进人工蜂群算法保持了ABC算法简单容易实现的特点，改善了算法的全局优化能力，便于收敛的同时也可以防止算法陷入局部最优解。
关键词： 人工蜂群算法;模拟退火;局部最优
中图分类号： TP391 文献标识码： A DOI：10.3969/j.issn.1003-6970.2020.07.003
本文著錄格式：张业清，李婧芳，胡鹏伟. 基于模拟退火思想的改进人工蜂群算法[J]. 软件，2020，41（07）：15-21
Improved Artificial Bee Colony Algorithm Based on Simulated Annealing
ZHANG Ye-qing1， LI Jing-fang1， HU Peng-wei2
（1. College of Information Science and Technology， Gansu Agricultural University， Lanzhou 730070， China;2. College of Mechanical and Vehicle Engineering， Changchun University， Changchun 130022， China）
【Abstract】： Aiming at the shortcomings of artificial bee colony algorithm （ABC） easy to fall into local extreme point， slow convergence in late evolution and poor optimization accuracy. Simulated annealing technology （SA） is introduced into the ABC algorithm， and an improved optimization algorithm is proposed. The hybrid optimization algorithm performs ABC and SA search in sequence at each temperature and is a two-layer serial structure. Since ABC provides a parallel search structure， a hybrid optimization algorithm transforms SA into a parallel SA algorithm. The probabilistic suddenness of SA ensures the diversity of the population， thus preventing the ABC algorithm from falling into a local minimum. The improved artificial bee colony algorithm based on simulated annealing maintains the characteristics of the ABC algorithm that is simple and easy to implement， improves the algorithm's global optimization ability， facilitates convergence， and prevents the algorithm from falling into the local optimal solution.
【Key words】： Artificial bee colony algorithm; Simulated annealing; Local optimal
0 引言
2005年，土耳其学者Karaboga提出一种人工蜂群算法[1]，这种算法主要依托了一种全新的群智能下的全局优化算法，它灵感是从蜂群在进行采蜜的行为中得到的。通过采蜜中的蜂群行为进行效仿，来提出的一种优化算法，采用该优化算法只要求我们对问题本身的优劣情况进行对比，不需要去深入了解某些问题的特殊性，在蜂群中只需了解局部工蜂的优化行为，来然后在整个蜂群中采用全局的优化情况进行对比，得出最优情况并进行突出表现，这样的算法对于收敛的速度提高很多，这也可以说是它为集群智能思想的重要体现。
作为一种新的集群智能优化算法，人工蜂群算法理论研究和应用已经成为新的研究热点，由于它在很多方面的优良性能，已经成为仿生智能计算机领域的一种重要优化算法。可是对于这种最基本的蜂群算法来讲，存在一定的弊端，它很容易陷入一定的局部优化现象和进化后期收敛速度较慢等缺点[2]，但是本文从防止其陷入局部最优解方面进行了改进，来提高该算法的性能，经过试验可以看出改进后的人工蜂群算法可以很好地预防模型陷入局部最优[1]。
1 人工蜂群算法
1.1 人工蜂群算法
在人工蜂群算法中，每次搜寻过程包括三个阶段内容[3-10]：
（1）该阶段下，对于采集位置随机分到各个工蜂之间，各个工蜂将对该负责位置的花蜜多少进行测量，测量结束后各个工蜂回到蜂巢进行蜜源信息额分享。
（2）完成各自信息挥汇报之后，蜜蜂在回到他们之前到达的地方，依照各自的视觉情况对采集位置进行排查，再去周围寻找一个新的位置下的蜜源。
（3）这时每个观察的蜂蜜将对工蜂分享的花蜜信息进行选择，如果该位置的蜜源才存在的花蜜量越大则此处的蜜源被选择到的概率就越大。
此时得到高蜜源信息的观察蜂召唤的蜜蜂就会有更多的花蜜量。在蜜蜂到达了其选定的位置后，基于蜜源位置的对比，进行采蜜的工蜂会依照其先前的自身的记忆在之前的位置进行新的选择，得到一个新的蜜源，当有一个位置的花蜜被采蜜蜂进行舍弃后，将有新的观察蜂对蜜源进行选定，来对舍弃的位置进行替换。在这个采蜜过程中，每次外出时只要求一致观察蜂去搜查新位置下的蜜源，同时要求进行观察的蜜蜂数量与进行采蜜工蜂的数量是一致的。
在该蜂群采蜜过程中，对于蜂群中进行采蜜和观察的蜜蜂数量基本保持为各自一半。同时对于每个位置只分配一个工蜂进行采蜜。我们可以理解成实际蜜源的数量与进行采蜜的数量是一样的。当出现在某一位置中的蜜源被进行观察和采蜜的工蜂采完后，此位置的采蜜蜂将会成为一个新的侦查蜜蜂随机寻找新的蜜源。
三种蜜蜂在不同的条件下可以相互转换，如下图。
在该算法当中，对于优化问题来讲，该解可能是存在某一位置下的蜜源，而适应度的函数值则对应该位置下的花蜜量的数量。解为观察或是进行采蜜的工蜂的数量。该算法包含以下几个步骤。
（1）在该算法下，有N个侦查蜂进行侦查任务，这也可以认为是该算法的可行解，同时N也代表了进行采蜜工作的工蜂的数量，也可代表着寻找到的蜜源的数量值。该算法中每个解（i=1，2，…，N）都可以认为是D维的向量，其中D也可以认为是参量的个数值。每一个蜜源吸引一个采蜜蜂，N个蜜源吸引N个采蜜蜂，采蜜蜂的位置即为蜜源的位置。
（2）在该算法进行完初始化之后，针对于蜜源的问题的最优解会通过三种蜜蜂进行寻找后得出，观察蜂或是进行采蜜的工蜂依照自身获得的信息内容在现有的特定区域下进行寻找来进一步获得新的蜜源的位置，并对该位置的花蜜量多少进行相应的测量，该测量值也可以认为是适应度函数对应的数值。通常在蜜蜂进行真实采蜜下，它们会对改位置中的蜜源多少进行判定并进一步得出此处的新蜜源的产值。在该计算模型中同样依靠这一原理。但是在此模型中，是不会对信息进行深一步的比较，一般是对蜜源进行随机的选定，同时依靠记忆来选定一个区域，依据下面的公式（2）進行分析，按照贪婪准则，如果一个区域中的蜜源高于另一个区域蜜源，他们会对蜜源较低的区域进行舍弃，并对区域进行记忆。完成所有区域的信息搜索后，他们会回到指定位置与观察的蜜蜂进行蜜源信息的分享，每一个观察蜂都会对其观察的蜜源量进行信息评估，并根据评估结果作为蜜源选择的依据。蜜源的收益度越高，吸引观察蜂的概率越大。
（3）对于进行采蜜的蜜蜂来讲，他通过本身的记忆信息对原位置进行判定，得出一个限定区域，对候选的花蜜量进行测量，依照贪婪准则对蜜源的位置进行选定。
对于一个位置内的蜜源进行选定的该概率情况进行选定方式可以表示为：
在上面的（1）式中，第i个解所对应适应度函数数值可以用
进行表示，该数值与第i个位置下蜜源的实际数量也是成正相关的;蜜源的实际数量我们采用N进行表示，这与进行采蜜的蜜蜂的数量是一致的。观察蜂与进行采蜜的蜜蜂采用这种方式来完成信息的交汇。
ABC模型采用以下公式从就的蜜源位置中产生一个新的候选蜜源位置，即：
式（2）中，与在集合中进行随机的选取，并且，rand（）在此式中代表了[-1，1]中的随机数值，蜜源在限定范围的实际产量有它来影响，同时对于限定区域它可以对工蜂获得的并且可以进行比较的区域进行代替。
对于上式（2）我们可以得出，在位置处的波动情况与和的参数差是正相关的。通过该原理，想要在蜜蜂进行搜寻的区域内短时间内得到最优解就要对步长进行缩短的调整。
每个候选蜜源位置产生后，其花蜜量与进行比较。如果出现了更好的蜜源位置，依照贪婪法则，旧的蜜源位置将会被替换。同时某未知的蜜源量在经过有限次搜索后蜜源含量任然么有改善，自该蜜源将会被放弃。
1.2 人工蜂群算法的四种选取过程
（1）全局形式的选择过程：观察蜂在一般情况下会采用这种方法，它们通过这种方式来对花蜜量最多的区域进行判定及选取，这也是对最优解的区域进行选取。见上式（1）所示。
（2）随机形式的选择过程：这种方法通常侦察蜂采用。
（3）区域形式的选择过程：这种方法可以同时被进行采蜜和观察的蜜蜂选取，依照该区域中的线管蜜源信息对记忆位置周围区域的蜜源量进行测定，见上式（2）所示。
（4）贪婪选择形式的过程：任何进行采蜜工作的蜜蜂均使用该方式，如果存在花蜜量更高的蜜源，蜜蜂将在其记忆中替代原有的花蜜量较少的蜜源，如果不存在将不会进行替换。
人工蜂群算法中，蜜蜂的采蜜行为和函数优化问题的对应关系如下表。
1.3 人工蜂群算法程序的实现步骤
1. 蜜蜂种群的初始化情况。在该程序的初始阶段，所有的蜜蜂全部以侦查蜂的形式出现，对全局进行搜索，因为他们对于各区域没有了解，依照所搜得到的蜜源来对花蜜进行评估，也就是“收益度”。
对于种群参数而言，只要有以下三个参数：
（1）蜜蜂的总体数量N，一般情况下我们会将观察蜂和进行采蜜的蜜蜂分别认为是N/2;
（2）对于某处蜜源的停留的最大搜索限制次数Limit;
（3）搜索过程中出现的最大迭代次数;
2. 依照上步得到的“收益度”数值，蜂群将被划分为两类即：观察蜂和采蜜蜂，得到收益度靠后的将变为观察蜂，而靠前的将变为采蜜蜂。此时观察蜂在舞蹈区进行等待，通过采蜜蜂传递的信息来对该区域的花蜜信息有一个掌握，对于花蜜量含量高的区域召唤观察蜂也会逐步增加，这是一个以概率形式来完成招募的过程。
3. 采蜜蜂将在原蜜源附近继续搜索并开展采蜜工作，并对该区域的花蜜量进行评估，依照贪婪法则对蜜源进行选取，来获得更多的花蜜。
4. 对于观察蜂而言，他们对于蜜源的选取是依据适应度进行概率性分配，在蜜源周围进行采蜜及蜜源寻找，在进行蜜源寻找过程中，同样遵循贪婪原则。
5. 如果在该蜜源区域搜索的次数已经超过了限定次数，但是还没发现更好的蜜源，它们将会放弃此区域，同时蜜蜂的角色也会发生改变，即观察蜂和采蜜蜂会变成侦查蜂，随机前往一个新位置的蜜源。
6. 对当前的所有蜜源进行记录，来找到全局的最优解，并跳转到第2步，循环此过程，结束的标志为符合最大迭代次数或是小于优化误差，最后得到全局的最优值。
2 建模过程实例
在该建模中建立人工蜂群算法的数学模型，同时该建模以典型的多峰值函数优化问题为分析背景。
（1）对于n=0时刻，随机生成个可行解，具体随机产生的可行解为：
（7）一旦出现符合停止要求的情况出现，则停止计算过程并得出最优适应度值以及与其相关的参数值，否则在回到第2步进行重新运算。
其中第（6）步主要是为了增强种群的多样性，防止种群陷入局部最优值，这一步骤可使种群搜索到最优值的概率得到提高。
3 基于模拟退火算法的改进人工蜂群算法
3.1 模拟退火算法原理分析
模拟退火算法这种算法是以固体退火原理为基础，在固体处于高温环境下，其内部的粒子在进行快速的无规则运动，同时具有很大的内能，但是在其处于常温时起内部的粒子最稳定，内能达到了最小，模拟退火算法也是根据这种原理进行设计的。
模拟退火算法通过概率统计展开随机性的迭代求解[11]，该方法模拟固体物质退火，进一步的解决了在算法进优化时易陷入局部最优解这一難题，同时在进行组合问题优化时可不过分依赖目标函数的初始值。对于该算法进行优化的目标函数来讲，它是对固体的内能进行了模拟求全部的解由固体的内能值进行表示，我们得到的最小内能值就是代表问题的最优解。让金属逐渐的冷却才能得到最低的内能值，这也是组合优化的重要前提。对于退火算法进行模拟式主要包含3个内容即：冷却、等温及加温过程[12]。在金属温度为T时，处于固体内部的粒子会处在一个相对平衡的状态，假设在该温度下固体的被能为E，该变量为
，则这时固体内部的粒子处于平衡状态下的概率可用来进行表示。但是随着温度的降低，其中的内能也最终将达到一个最低值[13]。
3.2 模拟退火思想寻找最小值问题
这种计算方法是依靠统计力学进行展开。在统计力学角度中分析，处于不同结构下的粒子有不同能量。不同的温度下，粒子能量不同，粒子的运动及排列形式也有所不同。当系统从高温条件下逐步的降低温度，直至完全的冷却，晶体最终会处于一种低能的状态[14-15]。
假如我们对于材料的状态采用粒子自身的能力进行定义，Metropolis算法可以认为退火过程采用了一个简单的数学模型进行表达。。这时我们假设E（i）为材料处在i状态下的能量，材料在处于T温度时，对于从i状态变为j状态则可以表示为以下规律：
（1）当E（i）小于等于E（j）时，状态的变化用下面概率呈现：
上式中，材料温度用T表示，而K代表波尔兹曼常数。
（2）当E（i）大于等于E（j）时，这种状态转换将被认可。
综上所述在一定温度下，材料进行了充分的转换后，会达到一种热平衡状态。如果出现温度降低的很大情况时，材料会以很大概率进入最小能量状态。
假设目标函数为：
要求得最优解，就要设定初始温度，同时对其进行初始化得到解x（0），通过x（0）得到解x?，分析x?是否接受成为新解x（1）依赖于一个概率密度函数（接受新解的概率），若新解大于旧解则以概率1接受新解，若新解小于旧解这个概率则以概率密度函数计算值接受，通常为小于1的情况。
在
温度下，对于新得到的解x?可以通过优化问题的解x（k）得到，分析接受x?成为新解x（k+1）是一定的概率问题。对
温度进行多次温度降低的转换后，得出。在的情况下对上述操作进行重复。整个过程可以认为逐渐的进行新解寻找和逐渐降低温度的过程，最后我们得到解就是该分析问题的最优解。
在下，x（k）的状态决定下一个新的状态x（k+1），与前面的状态情况时无关的，这是一个典型马尔可夫过程。如果存在缓慢下降温度但是每一状态下温度却又经过多次转换，致使在每个温度状态下都实现热平衡，这时将以概率1的形式进行全局的最优解表达。综上所述全局最优解可以通过模拟退火算法进行获取。
3.3 转移概率公式
容易看出其转移概率函数为指数函数，其自变量越大概率越大。首先不考虑常数系数K，K的作用仅限于人为调节，分两方面来考虑这一转移概率函数。
（1）解的差值不变，温度改变
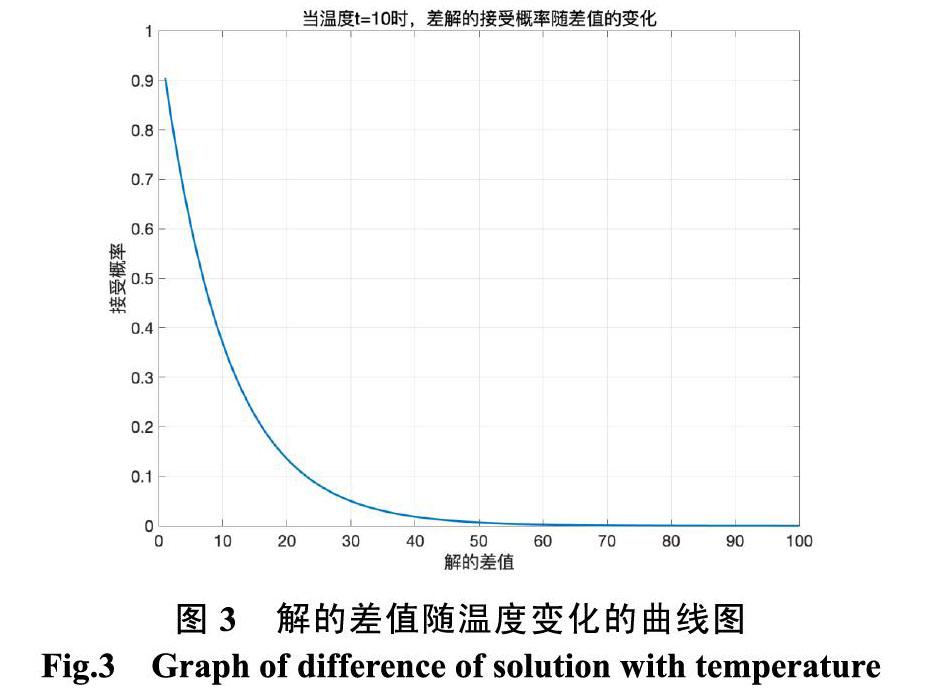
当解的差值不变时，其自变量的分子不变，分母越大，自变量越小，其负值越大，其因变量值越大，越接近1，其图像如图3所示。表明同一差值下，温度越高就越容易接受新的差解。
（2）溫度不变，解的差值改变
当温度不变时，其自变量的分母不变，差值越大分子越大，其负数越小，其因变量越小，越接近0，其图像如图4所示。表明同一温度下，差值越小就越容易接受新的差解。
对于智能算法而言，算法的前期搜索范围极大，当算法达到后期时，会慢慢进入收敛状态，即可能达到了全局或局部最优解，为此，本文从局部最优和全局最优两方面来考虑改进方法。
（1）局部最优解的搜索方法
本文方法的思想可以使解不断向解空间的最优解靠拢，可以有效的加快局部搜索的速度，使一个解空间可以以最快的速度达到局部最优解。
（2）全局最优解的搜索方法
由于智能算法的随机性，不能保证种群覆盖到全部的解集，很容易陷入局部最优解，同时在解的前期其移动步长过短，后期移动步长过长，故本文借助模拟退火算法的思想，引入“温度”，“接受概率”等概念来解决此问题。
（3）本文转移概率公式
Double delta = x_old-x_nei
Double cr = exp（delta/（1/process*100））
If （rdft（） X_new = x_old+（x_old-x_nei）*（rdft（）-0.5）* 2+（x_glo-x_old）*0.5*（rdft（））; }else{ X_new=x_old+（x_old-x_nei）*（rdft（）-0.5）*2; } 本优化方法以SA为思想，取K=100，t=1/process，process为算法运行的当前代数，当前邻居解与旧解的差值为分子。即：当运行代数较小时，1/process较大，温度较高，cr值较大，算法更容易向局部最优解靠拢。当运行代数较大时，1/process较小，温度较低，cr值较小，算法更容易扰乱原解，脱离局部最优解。 4 实验结果及分析 由于ABC算法的贪心算法找到的是局部最优解的情况，全局最优则是通过模拟退火算法获取。对于模拟退火算法来讲，它的基础是metropolis算法。Metropolis算法又称为metropolis抽样，其核心思想是当能量增加的时候以一定的概率接纳而非一味拒绝。基于此思想应用于基础的ABC算法上，经实验证明去的了较好的效果。传统的ABC算法在算法的任何阶段对于新解的产生，改变的步长都是一定的，本文通过引入模拟退火思想，使ABC在算法初期能以较大步长寻找新解，便于跳出局部最优;在算法后期以小概率接受步长较长的新解，便于收敛的同时也可以防止算法陷入局部最优解。为了验证基于模拟退火算法的人工蜂群算法的优化结果，本文对原始的三种优化算法以及我们的优化算法分别在三个不同的目标函数下进行200次的迭代，得到了如下实验结果： 4.1 第一组实验（目标函数为Rosenbroke函数） （1）第一种原始的新解产生函数（设置pp_ debug = 1），运行结果如下： Means of 200 runs： 9.808269901650287892 平均运行时间=： 0.055567155000000 second Min val：0.176049980984729904 （2）第二种改进方法（pp_debug = 2），此转移方法在第一种的基础上增加了全 局更新的思想，有利于达到全局最优解，但会陷入局部最优解，运行结果如下： Means of 200 runs： 27.444346569494861399 平均运行时间=： 0.056990765000000 second Min val：0.062116211823108072 （3）第三种转移方法（pp_debug = 3），次方法结合第一种和第二种，没有本质改 进，效果介于第一种和第二种之间，运行结果如下： Means of 200 runs： 15.291687887025133818 平均运行时间=： 0.057119505000000 second Min val：0.104958787969900436 （4）本文在引入模拟退火算法之后（即pp_ debug = 5）时，运行结果如下： Double delta = x_old-x_nei Double cr = exp（delta/（1/process*100）） If （rdft（） X_new = x_old+（x_old-x_nei）*（rdft（）-0.5）* 2+（x_glo-x_old）*0.5*（rdft（））; }else{ X_new=x_old+（x_old-x_nei）*（rdft（）-0.5）*2; } Means of 200 runs： 9.417805958074286110 平均运行时间=： 0.057688065000000 second Min val：0.011360413050712590 由运行结果可见解的平均值大大降低 4.2 第二组实验（目标函数为Griewank函数） 4.3 第三组实验（目标函数为Rastrigin函数） 经过以上三组实验结果可以看出，本文基于模拟退火算法的改进对三种不同优化目标函数下的结果均优于前三种算法且十分有效，在时间复杂度不增加的同时对平均结果和最优解的提升效果很大。 5 结论 本文将ABC和SA相结合，得到了一种改进后的的人工蜂群计算方法。这种方法不但保留基本人工蜂群算法具有的简单容易实现的优势，而且利用SA的概率突跳性，保证了群体的多样性，同时增强了收敛精度以及对于空间的探索能力，避免了原始方法的缺点。它不仅仅是算法上的改进，同时也体现了进化以及搜索形式的互补。能够很好地解决对于复杂问题的优化难题。这种改进的人工蜂群算法不论在性能还是优化效率层面，可以通过计算机仿真结果得出是明显优于基本ABC算法。 参考文献 An Idea Based On Honey Bee Swarm For Numerical Optimization. Karaboga. D. Technical Report-TR06. 2005
Abachizadeh M， Yazdi M， Yousefi-Koma A. Optimal tuning of pid controllers using artificial bee colony algorithm[C]// 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics（AIM）， 2010： 379-384.
Tereshko V. Reaction-diffusion model of a honeybee colonys foraging behavior[C]. Parallel Problem Solving from Nature PPSN VI. Springer Berlin Heidelberg， 2000： 807-816.
Tereshko V， Lee T. How information-mapping patterns determine foraging behaviour of a honey bee colony[J]. Open Systems & Information Dynamics， 2002， 9（02）： 181-193.
Lucic P， Teodorovic D. Bee system： modeling combinatorial optimization transportation engineering problems by swarm intelligence[C]. Preprints of the TRISTAN IV triennial symposium on transportation analysis. 2001： 441-445.
Teodorovi?D， DellOrco M. Bee colony optimization-a cooperative learning approach to complex transportation problems[C]. Advanced OR and AI Methods in Transportation： Proceedings of 16th Mini-EURO Conference and 10th Meeting of EWGT （13-16 September 2005）. Poznan： Publishing House of the Polish Operational and System Research. 2005： 51-60.
Yang X S. Engineering optimizations via nature-inspired virtual bee algorithms[M]. Artificial Intelligence and Knowledge Engineering Applications： A Bioinspired Approach. Springer Berlin Heidelberg， 2005： 317-323.
Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Technical report-tr06， Erciyes University， engineering faculty， computer engineering department， 2005.
Karaboga D， Akay B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation， 2009， 214（1）： 108-132.
Karaboga D， Akay B. A survey： algorithms simulating bee swarm intelligence[J]. Artificial Intelligence Review， 2009， 31（1-4）： 61-85.
Karaboga D.An idea based on honey bee swarm for numerical optimization， TR06[R].Kayseri，Turkey： Erciyes University， 2005.
何堯， 刘建华， 杨荣华. 人工蜂群算法研究综述[J]. 计算机应用研究， 2018， 35（05）： 1281-1286.
陶重犇， 雷祝兵， 李春光， 等. 基于改进模拟退火算法的搬运机器人路径规划[J]. 计算机测量与控制， 2018， 26（7）： 182-185.
裴小兵， 贾定芳. 基于模拟退火算法的城市物流多目标配送车辆路径优化研究[J]. 数学的实践与认识， 2016， 46（2）： 105-113.
张磊. 基于模拟退火算法的粮食调拨路径规划[J]. 粮食加工， 2019， 44（04）： 7-9.
