加权空-谱局部信息保持极限学习机的高光谱图像分类算法

2020-12-24邢钰佳闫德勤刘德山王军浩

软件 2020年7期

邢钰佳闫德勤刘德山王军浩

摘要：高光谱图像的分类研究是高光谱图像处理与应用的重要环节。为有效提取高光谱遥感图像的空间信息和光谱信息，本文基于极限学习机提出新的研究。在模式识别和机器学习领域，极限学习机以其简单、快捷和良好的泛化能力得到越来越多的关注。但由于在高光谱遥感图像的学习过程中极限学习机缺乏对空间信息和光谱信息的有效提取，无法在分类中提供良好的分类结果。为此，基于谱局部信息的思想构造本文的研究框架，提出一种加权空-谱局部信息保持极限学习机分类算法。为验证所提算法的有效性，本文在两组常用的高光谱数据集Indian Pines和University of Pavia上进行实验，通过与传统的分类算法SVM和目前较为流行的分类算法KELM，KCRT-CK，MLR和LPKELM相比，本文算法具有较好的分类精度。

关键词：极限学习机;高光谱遥感图像分类;加权空-谱;局部信息保持

中图分类号： TP3 文献标识码： A DOI：10.3969/j.issn.1003-6970.2020.07.023

本文著录格式：邢钰佳，闫德勤，刘德山，等. 加权空-谱局部信息保持极限学习机的高光谱图像分类算法[J]. 软件，2020，41（07）：113-119+135

Hyperspectral Image Classification Algorithm for Weighted Spatial SpectralLocality Information Preserving Extreme Learning Machine

XING Yu-jia， YAN De-qin， LIU De-shan， WANG Jun-hao

（Department of Computer Science， Liaoning Normal University， Dalian 116081， China）

【Abstract】： Classification of hyperspectral images is an important part of hyperspectral image processing and application. In order to effectively extract the spatial and spectral information of hyperspectral remote sensing images， this paper proposes a new study based on extreme learning machines. In the field of pattern recognition and machine learning， extreme learning machines have attracted more and more attention due to their simplicity， speed and good generalization capabilities. However， due to the lack of effective extraction of spatial information and spectral information during the learning process of hyperspectral remote sensing images， extreme learning machines cannot provide good classification results in classification. To this end， based on the idea of spectral local information， a research framework for this paper is constructed， and a weighted spatial spectral locality information preserving extreme learning machine classification algorithm is proposed. In order to verify the effectiveness of the proposed algorithm， this paper performs experiments on two commonly used hyperspectral data sets， Indian Pines and University of Pavia， and compares with the traditional classification algorithm SVM and the currently popular classification algorithms KELM， KCRT-CK， MLR Compared with LPKELM， our algorithm has better classification accuracy.

【Key words】： Extreme learning machine; Hyperspectral image classification; Weighted spatial spectral; Locality information preserving

0 引言

高光谱遥感图像（HSI）是由数百个光谱带组成的3维立体图像，如何从中提取大量信息应用于图像分类是遥感图像领域面临的一项挑战。目前，许多机器学习算法均被应用于高光谱遥感图像的分类任务中，诸如K-近邻（KNN）^[1]，Logistic回归^[2，3]，人工神经网络（ANN）^[4]等。在这些方法中，支持向量机（SVM）^[5]已经被证明在小样本且包含噪声的情况下具有最优的分类精度。然而在高光谱遥感图像的分类任务中存在着较为明显的Hughes现象^[6]，如果将原始频段未经处理直接应用于机器学习算法，将会对分类精度产生较大的计算负担。为应对这种问题，文献[7]将图形模型转移到地址频带选择问题上，通过捕获高光谱带之间的多重依存关系，提供了一种有效的搜索策略来选择最佳频带。文献[8]使用确定点处理来选择代表性频带，并保留频谱频带的相关原始信息，通过在所选频段上执行多个拉普拉斯特征图（LE）来进一步提高分類性能。文献[9]为整合光谱和空间信息达到更好的分类效果，提出了一种获取空间信息简洁有效的方法引导式过滤算法。文献[10]采用稀疏表示和加权复合特征（WCF）的概率建模来得出优化的输出权重并提取空间特征，以构建一种高光谱遥感图像光谱空间分类的新框架。

最近，Huang等人^[11]提出了一种有效的单隐层前馈神经网络（SLFN）算法，即极限学习机（ELM）。极限学习机随机生成与训练样本无关的节点参数。因此，用户只需要预定义关于网络架构的参数，即隐藏层节点的数量，这使得算法在调优过程中节省了大量时间。与此同时，极限学习机利用神经网络机制分析性地获取输出层的输出权重，而支持向量机则采用迭代优化算法进行训练获得输出权重，这就使极限学习机的学习速度比支持向量机更快。此外，在多分类任务中，极限学习机使用OAA策略，而支持向量机使用OAO策略，这就使极限学习可以进一步缩短训练过程和测试过程中的计算时间^[12]。文献[13]提出了一种将两级融合（即特征级融合和决策级融合）与全局Gabor特征和原始频谱特征一起应用于局部二进制模式（LBP）提取特征的框架，并采用结构非常简单的高效极限学习机作为分类器来提高高光谱遥感图像的分类效果。文献[14]构建了多层ELM以实现来自HSI的有效有限元分析。文献[15]提出了一种用于遥感图像分类的基于极限学习机的异构域自适应（HDA）算法。然而，高光谱遥感图像是通过远距离遥感拍摄捕捉的，会出现信号失真、格式错误和频谱杂波等问题^[16]。不充分和错误标记的样本使得高光谱遥感图像分类变得更具挑战性^[17]，为应对这种问题，文献[18，19，20]提出一种基于核的方法并将其应用于高光谱遥感图像的分类任务中。基于核的方法通过将数据从原始输入空间映射到高维Hilbert空间来提高学习模型对线性不可分数据的分离能力，支持向量机和极端学习机是近年来用于基于核的高光谱遥感图像分类领域的主要方法^[18，21-23]。文献[24]提出了一种基于核的ELM，通过实验验证了基于核的ELM在土地覆盖分类中的分类效果优于SVM，并且在很大的程度上降低了计算复杂度。文献[25]提出一种新的广义复合核框架被用于高光谱图像分类。文献[26]将高光谱图像数据样本的流行结构引入到了ELM的模型中，来提高其分类效果。基于核的极限学习机作为一种特殊的单隐层神经网络，学习时间相对较短，并为最小范数和最小二乘的非线性问题提供更优的解决方案而脱颖而出。

研究表明，基于核的极限学习机作为一种特殊的单隐层前馈神经网络在遥感图像分类任务中取得了良好的分类效果，但是基于核的极限学习机在有监督的高光谱遥感图像分类中仍存在着学习不充分、缺乏空间信息等问题。本文为充分利用高光谱遥感图像的空谱信息，基于流形学习的思想以及最新核技术方法的启发^[27-29]，提出一种加权空-谱局部信息保持极限学习机（weighted spatial spectral locality information preserving extreme learning machine，WSSLPKELM）。该算法利用高光谱遥感图像的空间信息和光谱信息的有效结合，来对高光谱遥感图像进行预处理，有效地提高了高光谱遥感图像的分类精度，并利用流形学习的思想将高光谱遥感图像数据样本的几何结构信息和判别信息引入到ELM模型中，弥补了ELM在高光谱遥感图像分类中学习不充分、空间信息利用不充分的问题。为了评价和验证所提方法的有效性，使用Indian Pines，University of Pavia两个常用的高光谱遥感图像数据集进行实验，将本文所提出的方法与SVM^[5]，KELM^[24]，KCRT-CK^[20]，MLR^[25]，LPKELM^[26]算法进行对比，实验结果表明本文所提算法具有最优的分类效果。

本文的其余部分安排如下：第二部分介绍核极限学习机;第三部分介绍提出的加权空-谱局部信息保持极限学习机算法;第四部分利用两个高光谱数据集进行实验，并给出实验结果及分析;第五部分对所提算法进行总结。

3 高光譜遥感图像分类实验

3.1 实验数据

在实验中，使用Indian Pines和University of Pavia两个高光谱数据集来评估所提出算法的性能。两个HSI图像的简要介绍如下。

印度松树Indian Pines：该图像是被AVIRIS传感器收集在印第安纳州西北部的印度松树测试场地上的。图像大小为145×145像素，有200个波段，波长范围为400-2500 nm，被分为16类。通过去除覆盖吸水区域的频带，频带的数量已减少到200。由于所有可用类别中混合像素的显著存在以及每类可用标记像素的不平衡数量，针对此场景的分类问题具有十足的挑战性。印度松树高光谱遥感图像在灰度和地面实况图中的第25个波段有9个不同的类别，如图2所示。

帕维亚大学University of Pavia：该图像是在意大利北部帕维亚的一次飞行活动中被ROSIS传感器采集的。图像大小为610×340像素（覆盖0.4-0.9μm的波长范围），有103个光谱带，波长在430和860nm之间。有九个不同的类。在本次实验中，去除12个最有噪声的频带，使用115个频带中的103个。帕维亚大学HSI在灰度和地面实况图中的第50个波段有9个不同的类别，如图3所示。

3.2 实验和参数设置

对于两个图像，随机选择来自每个类别的1%标记样品用于训练，并且将剩余样品用于测试。加权空-谱算法（WSS）的窗口大小。本文所提算法WSSLPKELM使用RBF核。在本文中，通过总体分类精度（OA），平均分类精度（AA）和kappa系数来比较不同的算法，其中OA是测试集中分类正确的样本个数占所有样本个数的比例，AA是每个类的分类准确度。所有实验均在具有4.00GB RAM的Intel i3-3240 3.40GHz机器上使用MATLAB R2011a进行。

3.3 實验结果与分析

3.3.1 Indian Pines图像数据实验结果

在本节中，将本文所提算法WSSLPKELM与SVM，KELM，KCRT-CK，MLR，LPKELM算法的分类结果进行对比。通过对比测试集上的分类精度OA，AA和kappa系数来衡量每种算法的分类性能。六种分类方法在Indian Pines图像数据上的分类结果如表1所示。

由表1可知，WSSLPKELM算法与SVM，KELM，KCRT-CK，MLR，LPKELM算法相比，总体分类精度OA，平均分类精度AA和Kappa系数均有所提升。

3.3.2 University of Pavia图像数据实验结果

在本节中，将本文所提算法WSSLPKELM与SVM，KELM，KCRT-CK，MLR，LPKELM的分类结果进行对比。通过对比测试集上的分类精度OA，AA和kappa系数来衡量每种算法的分类性能。六种分类方法在University of Pavia图像数据上的分类结果如表2所示。

表2给出六种不同算法在University of Pavia图像数据上的分类精度OA，AA和Kappa系数。可以看出WSSLPKELM算法的分类结果要优于SVM，KELM，KCRT-CK，MLR，LPKELM算法。

通过表1和表2的对比实验结果可以看出，WSSLPKELM算法的分类性能优于其他五种分类算法，其原因在于WSSLPKELM结合高光谱遥感图像的空间结构特性，充分考虑高光谱遥感图像像素间在空间上的分布特性，利用高光谱遥感图像空间信息和光谱信息的结合对高光谱遥感图像进行预处理，有效地提高高光谱遥感图像的分类精度，并利用流形学习的思想将高光谱遥感图像数据样本的几何结构信息和判别信息引入到核极限学习机模型中，弥补核极限学习机在高光谱遥感图像分类中学习不充分、空间信息利用不充分等问题。

3.4 WSSLPKELM的参数分析

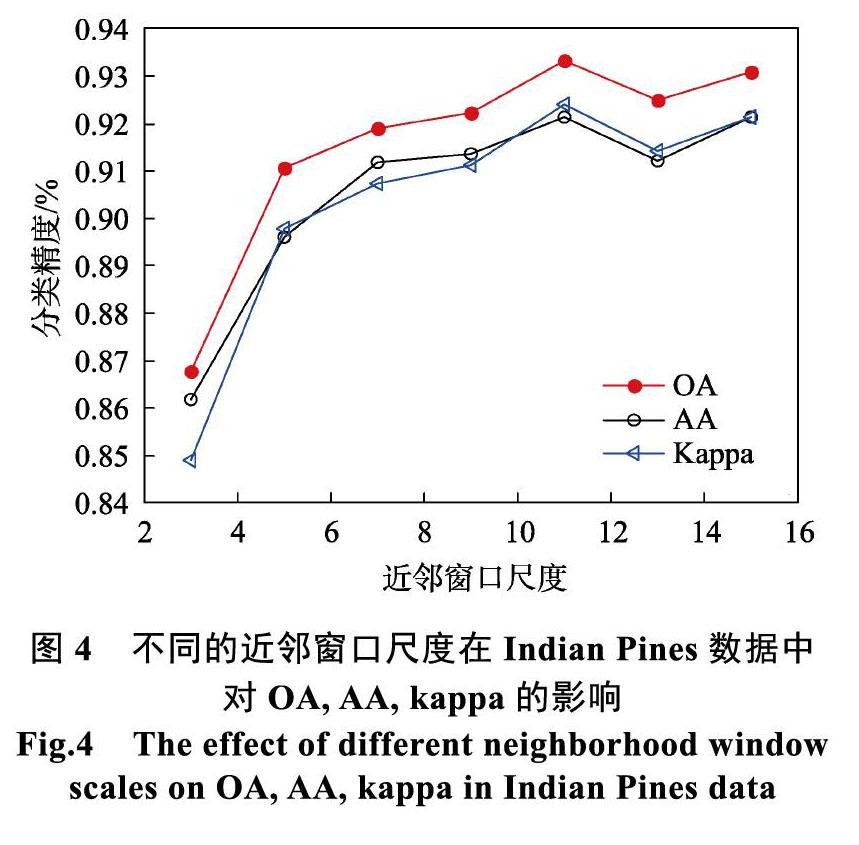
在本节中，重点分析一下两种不同遥感数据集下近邻窗口尺度w对WSSLPKELM算法的性能是如何影响的。加权空谱算法的窗口大小，核极限学习机使用RBF核，实验结果如图4、5所示。

根据图4可以看出，在Indian Pines数据集上分类精度总体趋势上随着近邻尺度的增长先增后降。当近邻窗口大小达到11时算法具有最优的分类精度，而后在近邻窗口达到13时分类精度降低较为明显。通过分类精度可以反映出近邻尺度的大小影响着算法的分类精度，综合多角度因素本文在实验中将近邻窗口尺度大小设置为11。

根据图5可以看出，在University of Pavia数据集上分类精度总体趋势上随着近邻尺度的增长先增后降。当近邻窗口大小达到13时算法具有最优的分类精度，而后在近邻窗口达到15时分类精度降低较为明显。通过分类精度可以反映出近邻尺度的大小影响着算法的分类精度，综合多角度因素本文在实验中将近邻窗口尺度大小设置为13。

4 结束语

本文中提出一种新的加权空-谱局部信息保持极限学习机WSSLPKELM。为了更加有效的提高高光谱遥感图像的分类精度，该算法通过以下策略进行处理。首先，该算法通过将高光谱遥感图像的空间信息和光谱信息结合起来对高光谱遥感图像进行预处理;然后，捕获预处理数据内部的流形正则化框架并通过局部保持算法LPP获取数据的判别性离散度矩阵;最后，将判别性离散度矩阵引入到核极限学习机中对高光谱遥感数据进行分类。通过与SVM，KELM，KCRT-CK，MLR，LPKELM算法进行比较，可以充分地证明本文所提算法WSSLPKELM针对高光谱遥感数据具有较好的分类效果。但是，由于相关预处理及流形框架以正则项添加到目标函数中，在一定程度上增加了算法的计算复杂度，在接下来的科研中将重点针对此方面进行重点突破。

参考文献

Kuo B C， Yang J M， Sheu T W， et al. Kernel-based KNN and Gaussian classifiers for hyperspectral image classification [C]//IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium. IEEE， 2008， 2： II-1006-II-1008.
B?hning D. Multinomial logistic regression algorithm[J]. Annals of the institute of Statistical Mathematics， 1992， 44（1）： 197-200.
Li J， Bioucas-Dias J M， Plaza A. Semisupervised hyperspectral image segmentation using multinomial logistic regression with active learning[J]. IEEE Transactions on Geoscience and Remote Sensing， 2010， 48（11）： 4085-4098.
Ratle F， Camps-Valls G， Weston J. Semisupervised neural networks for efficient hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing， 2010， 48（5）： 2271-2282.
Melgani F， Bruzzone L. Classification of hyperspectral remote sensing images with support vector machines[J]. IEEE Transactions on geoscience and remote sensing， 2004， 42（8）： 1778-1790.
Joy A A， Hasan M A M， Hossain M A. A Comparison of Supervised and Unsupervised Dimension Reduction Methods for Hyperspectral Image Classification[C]//2019 International Conference on Electrical， Computer and Communication Engineering （ECCE）. IEEE， 2019： 1-6.
Yuan Y， Zheng X， Lu X. Discovering diverse subset for unsupervised hyperspectral band selection[J]. IEEE Transactions on Image Processing， 2016， 26（1）： 51-64.
Zheng X， Yuan Y， Lu X. Dimensionality reduction by spatial-spectral preservation in selected bands[J]. IEEE Transactions on Geoscience and Remote Sensing， 2017， 55（9）： 5185- 5197.
Wang L， Zhang J， Liu P， et al. Spectral-spatial multi-feature- based deep learning for hyperspectral remote sensing image classification[J]. Soft Computing， 2017， 21（1）： 213-221.
Cao F， Yang Z， Ren J， et al. Sparse Representation-Based Augmented Multinomial Logistic Extreme Learning Machine With Weighted Composite Features for Spectral–Spatial Classification of Hyperspectral Images[J]. IEEE Transactions on Geoscience and Remote Sensing， 2018， 56（11）： 6263- 6279.
Huang G B， Zhu Q Y， Siew C K. Extreme learning machine： theory and applications[J]. Neurocomputing， 2006， 70（1-3）： 489-501.
Huang G B， Zhou H， Ding X， et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems， Man， and Cybernetics， Part B （Cybernetics）， 2011， 42（2）： 513-529.
Li W， Chen C， Su H， et al. Local binary patterns and extreme learning machine for hyperspectral imagery classification[J]. IEEE Transactions on Geoscience and Remote Sensing， 2015， 53（7）： 3681-3693.
Cao F， Yang Z， Ren J， et al. Local block multilayer sparse extreme learning machine for effective feature extraction and classification of hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing， 2019.
Zhou L， Ma L. Extreme Learning Machine-Based Heterogeneous Domain Adaptation for Classification of Hyperspectral Images[J]. IEEE Geoscience and Remote Sensing Letters， 2019.
Bolton J， Gader P. Application of multiple-instance learning for hyperspectral image analysis[J]. IEEE Geoscience and Remote Sensing Letters， 2011， 8（5）： 889-893.
Camps-Valls G， Tuia D， Bruzzone L， et al. Advances in hyperspectral image classification： Earth monitoring with statistical learning methods[J]. IEEE signal processing magazine， 2013， 31（1）： 45-54.

Camps-Valls G， Gómez-Chova L， Calpe-Maravilla J， et al. Robust support vector method for hyperspectral data classification and knowledge discovery[J]. IEEE Transactions on Geoscience and Remote sensing， 2004， 42（7）： 1530-1542.

Han M， Liu B. Ensemble of extreme learning machine for remote sensing image classification[J]. Neurocomputing， 2015， 149： 65-70.

Li W， Du Q， Xiong M. Kernel collaborative representation with Tikhonov regularization for hyperspectral image classification[J]. IEEE Geoscience and Remote Sensing Letters， 2014， 12（1）： 48-52.

Mountrakis G， Im J， Ogole C. Support vector machines in remote sensing： A review[J]. ISPRS Journal of Photogrammetry and Remote Sensing， 2011， 66（3）： 247-259.

Pal M， Maxwell A E， Warner T A. Kernel-based extreme learning machine for remote-sensing image classification[J]. Remote Sensing Letters， 2013， 4（9）： 853-862.

Chen C， Li W， Su H， et al. Spectral-spatial classification of hyperspectral image based on kernel extreme learning machine[J]. Remote Sensing， 2014， 6（6）： 5795-5814.

Pal M， Maxwell A E， Warner T A. Kernel-based extreme learning machine for remote-sensing image classification[J]. Remote Sensing Letters， 2013， 4（9）： 853-862.

Li J， Marpu P R， Plaza A， et al. Generalized composite kernel framework for hyperspectral image classification[J]. IEEE transactions on geoscience and remote sensing， 2013， 51（9）： 4816-4829.

何陽，闫德勤，刘德山. 局部信息保持极限学习机的遥感图像分类[J]. 计算机应用与软件， 2019， 36： 1.

Pal M， Maxwell A E， Warner T A. Kernel-based extreme learning machine for remote-sensing image classification[J]. Remote Sensing Letters， 2013， 4（9）： 853-862.

Li L， Wang C， Li W， et al. Hyperspectral image classification by AdaBoost weighted composite kernel extreme learning machines[J]. Neurocomputing， 2018， 275： 1725-1733.

阿茹罕，何芳，王标标. 加权空-谱主成分分析的高光谱图像分类[J]. 国土资源遥感， 2019， 31（2）： 17-23.

Pal M， Maxwell A E， Warner T A. Kernel-based extreme learning machine for remote-sensing image classification[J]. Remote Sensing Letters， 2013， 4（9）： 853-862.

Argyriou A， Micchelli C A， Pontil M. When is there a representer theorem？ Vector versus matrix regularizers[J]. Journal of Machine Learning Research， 2009， 10（Nov）： 2507-2529.