基于三阶段DEA中部地带物流产业效率测度研究

刘 莉，孟庆浩

(湖南工业大学 商学院， 湖南 株洲 412007)

一、研究背景

近年来，随着我国经济的快速发展，物流业得到了快速发展。物流业是我国经济发展的动脉，是极具发展前景的战略性复合型产业[1]。资源的有效利用一直以来是经济学领域的热点研究问题，物流产业效率的研究对产业的振兴与发展具有重要作用[2]。我国中部地带地理位置处于东西地带交界处，拥有丰富资源和雄厚的工业基础，又是全国的重要交通枢纽，使得中部地带物流业的发展速度较快。尤其是在 “供给侧”改革的过程中，物流业降本增效取得了战略性成果[3]。中部地带物流产业从传统的侧重速度的发展方式逐渐向侧重效率和质量的发展方式转变，对中部地区经济发展发挥着越来越重要的作用。

现代物流业对经济发展有着重要作用，物流效率成为国内外研究的热点问题。国外学者研究主要集中在宏观和微观角度评价物流效率的主体。在宏观角度研究方面，Schøyen等运用数据包络分析法(Data Envelopment Analysis,DEA)的CCR模型对2002—2008年挪威等北欧国家以及英国物流产业的关键节点(集装箱港口)的技术效率和规模效率进行了研究[4]。Markovits-Somogyi等提出了一种新的DEA-PC(成对比较)评估效率的新方法，将数据包络分析法与层次分析法相结合来研究欧洲29个国家的物流产业效率[5]。在微观角度研究方面，相关研究主要集中在物流企业的效率和绩效方面，Ross等结合DEA方法建立了新型综合标杆分析法对配送企业的生产率进行了分析[6]。Zhou等提出中国第三方物流企业效率评价准则，并分析中国第三方物流企业提高物流竞争力的方法[7]。Zhang等从财务、客户、业务和创新4个层面建立了适合中国第三方中小物流企业的绩效评价指标体系[8]。Shaik等研究了对企业逆向物流效率提高的新方法，使用一种称为决策试验和评估实验室(DEMATEL)的有效方法进行分析，并提出了改善企业绩效的建议[2]。

国内学者对物流产业效率的研究主要集中在宏观区域物流产业效率方面。例如，唐建荣等人运用方向距离函数模型测算中国31个省的物流产业效率，得知中国物流产业效率总体上呈现下降趋势，物流产业效率区域差异明显，物流产业效率在空间上呈现显著的正相关性[9]。郑秀娟使用改进的随机前沿模型，对物流业技术效率增进的时空差异验证，证实了全国物流产业规模效率的增长，未获得技术效率的递增，而且局部地区物流产业效率不平衡[10]。魏国辰等人以从业人员、固定资产投入和物流网络里程数为投入要素，货运量和物流业产值增加值为输出变量，使用超效率DEA模型对长江经济带物流产进行了分析[11]。杨传明考虑经济增长与环境负荷关系，应用三阶段DEA模型，测算低碳约束下江苏物流产业效率，实证结果显示，江苏在沿海省份中产业效率处于中上水平，技术效率和规模效率仍需提升[12]。

综上所述，学者对于物流产业效率的研究主要集中于区域时空差异性分析、低碳方面的物流效率、地区物流产业效率影响因素分析的研究等。在研究区域，主要集中在全国省市、西部地区以及对省份的物流产业效率研究，而对中部地带物流产业效率的研究则比较少。在研究方法上，呈现多样化和多种方法结合的趋势，这也导致研究结论的差异性。学者对于物流产业效率的测量的关注较多，但是对于影响物流产业效率的影响因素分析偏少。因此，本文使用三阶段DEA模型对中部地带各省市物流产业效率进行测算，三阶段DEA模型优于传统DEA模型，可以剔除环境因素和随机因素对效率测算的影响，能更加真实地反映效率情况，从而更真实地分析中部地带物流业的现状，为中部地带物流产业的发展提供参考。

二、研究方法

1978年，数据包络分析法(Data Envelopment Analysis,DEA)是由3位著名运筹学家A.Charnes、W.W.Cooper和E.Rhodes首次提出的，此时被称为“一阶段”DEA或传统DEA。之后，Fried等指出传统DEA模型未考虑环境因素，他们探讨并提出了剔除环境因素对评价的影响，此时被称为“二阶段”DEA[13]。后来，Fried等考虑环境因素和随机噪声对评价对象的影响，剔除了传统DEA未考虑到的环境因素和随机噪声，以能更加准确地分析决策单元内部管理无效率的问题，此过程被称为“三阶段”DEA[14]。为更加准确测算中部地带物流产业效率，本文使用三阶段DEA模型对中部地带物流产业效率进行测算。下面具体介绍三阶段DEA的步骤。

(一)第一阶段：传统DEA测算

A.Charnes等人于1978年提出的数据包络分析法(Data Envelopment Analysis,DEA)是运用运筹学模型对多个相同类型的输入和输出的决策单元(Decision Making Unit,DMU)进行相对效率评估的线性规划方法[15]。物流产业包含的范围广，对物流产业效率评价的指标也比较多，并且各指标之间具体的函数关系确定困难，而DEA模型有着使用方便和应用广泛的特征，适用于解决指标间不确定函数关系。DEA模型主要包括规模报酬不变的模型(CCR)和规模报酬可变的模型(BCC)，本文使用BCC模型对中部地带物流产业效率进行分析，计算出物流产业效率值、投入目标值和松弛变量值等结果。BCC模型如式(1)所示。

(1)

式中:α1，α2,…,αn为对偶变量；s-,s+为松弛变量；β为各决策变量(DMU)的技术效率值(TE)。

(二)第二阶段：随机前沿模型(SFA)回归和调整变量

1.SFA模型回归

传统的DEA模型在测算效率时，实际上会受到环境因素、随机噪声和管理无效率的影响。第二阶段主要考察(SFA)模型的必要性和对原始投入变量进行调整。构造SFA模型，以第一阶段DEA测得松弛变量作为第二阶段SFA的被解释变量，用外部环境和随机误差作为解释变量进行回归分析，从而准确反映管理无效率对决策单元的影响。SFA回归模型公式如公式(2)所示。

Snk=fn(Zk；βn)+Vnk+Unk；n=1,2,3,…,N；k=1,2,3,…,K

(2)

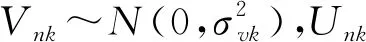
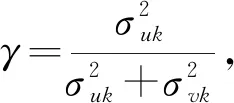
2.调整变量

(1)对于投入变量的调整，关键点是如何将综合误差项分离随机误差项Vnk和对管理无效率的估计公式确定。本文借鉴陈巍巍[17]、Jondrow[19]、罗登跃[20]等学者所采用的管理无效率估计公式：

(3)

(2)在对决策单元投入变量进行调整，剔除外部环境和随机因素的影响时，本文采用增加法调整投入要素:

n=1,2,3，…，N；k=1,2,3，…，K

(三)第三阶段：将调整后的变量用DEA模型测算

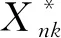
三、指标选择及数据来源

(一)物流产业投入产出指标选择及数据来源

目前，国内外的产业体系都没有对“物流产业”进行明确的划分。现在物流产业是交通运输、仓储和邮电等行业的复合型服务行业，而且据最新的《中国物流统计年鉴》显示，中国的交通运输、仓储和邮电业产值在物流总产值上占的比重较大，达到80%以上，故选择交通运输、仓储和邮电业的数据来反映物流业的发展水平[12]。本文以中国中部地带8省市，即山西省、吉林省、黑龙江省、安徽省、江西省、河南省、湖北省、湖南省为研究对象，将研究区间2013—2017年指标数据取平均值[17，21]来进行研究，研究的数据来源于2013—2017年《中国统计年鉴》以及各省份的省市统计年鉴。

1.投入指标选择

2.产出指标选择

物流产业产出指标主要体现在物流业增加值、货物周转量两个方面。结合相关文献和中部地带实际情况，本文选取物流业增加值和货物周转量作为测算中部地带物流效率产出指标。物流业增加值(单位：亿元)以交通运输、仓储和邮政业的增加值数据表示。货物周转量(亿吨/公里)采用铁路、内河、公路3种运输方式总和进行衡量。

(二)环境变量的选择

通过查阅相关文献可知，影响物流产业效率的因素一般包括经济发展水平、政府支持、区位优势等因素[24]。基于对以往文献的分析和地区物流产业的状况，结合数据的可得性和研究的目的，本文进行研究所采用的物流产业的影响因素包括经济发展水平、政府支持等方面。政府支持度(%)，政府对物流业从资金和政策的支持，对物流业的发展有着极大的帮助作用。本文采用交通运输、仓储和邮政业支出占全国财政支出的比重衡量[25]，可以更加宏观地评价政府对物流业的重视程度。经济发展水平(亿元)、地区经济发展水平高低对物流业的发展有重要的影响,本文采用各省市的GDP总值衡量[26]。

四、基于三阶段DEA的中部地带物流产业效率的实证分析

文中中部地带由最新三分法将中国划分成东部、中部和西部地带，其中中部地带包含山西省、吉林省、黑龙江省、安徽省、江西省、河南省、湖北省、湖南省等8省[27-28]。根据上文对物流产业效率投入和产出指标以及影响因素的选择，接下来对中部地带物流产业效率的研究分3个阶段进行。第一阶段，运用DEA模型对中部地带物流产业效率进行测算和分析。第二阶段，以第一阶段各投入变量的松弛变量作为被解释变量，以经济发展水平和政府支持作为解释变量，建立SFA模型进行回归分析及对投入指标进行调整。第三阶段，根据第二阶段调整过后的投入指标，重复第一阶段的中部地带物流产业效率的测算。

(一)第一阶段传统DEA实证结果

测算中部地带物流产业效率是对中部地带各省市分析物流业情况的基础。根据上文设定的投入和产出指标，同时在获取2013—2017年的中部地带8省市的物流产业的面板数据的基础上，选取投入导向的BBC模型测算各省市的物流业发展水平。对中部地带物流产业效率进行测算可以得到综合效率(TE)、技术效率(PTE)和规模技术效率(SE)。中部地带各省市的综合效率(TE)反映了各地区物流业的资源配置能力、资源使用效率等多方面的能力；技术效率(PTE)反映了各地区物流产业的管理水平和技术进步的情况，是在考虑管理、技术等因素下的效率；规模效率(SE)反映了各地区物流业的规模水平和增长的空间的情况，是在考虑自身规模影响下的效率。利用DEAP 2.1软件计算2013—2017年的中部地带8个省市的物流产业效率结果如表1所示。

表1 2013—2017年中部地带物流产业效率值

由表1可知，在不考虑环境因素和随机因素的情况下，可以得出以下结论：

(1)整体而言，中部地带各省的物流产业效率的平均综合效率为0.923，平均技术效率为0.964，平均规模效率为0.955。其中，山西省、安徽省、江西省、河南省和湖南省物流产业效率达到最优，DEA值为1，说明这5个省的物流产业效率投入和产出处于最好状态；而从吉林省、黑龙江省和湖北省物流效率观测值可知，中部物流产业效率未达到效率的前沿面，大多数效率都低于中部地带效率的均值，说明这3个省的物流产业效率水平较低。

(2)吉林省、黑龙江省和湖北省的物流效率观测值虽未达到效率的前沿面，但各省的规模报酬都处于规模报酬递增的状态，说明吉林省、黑龙江省和湖北省应当在现有的管理水平下，增加资源的投入，从而提升地区物流产业效率。

(3)从对各省市的物流效率分析来看，吉林省技术效率达到效率前沿面，而规模效率仅为0.823，说明吉林省的物流业有较好技术和管理水平，该省的物流产业效率在规模上有较大的提升空间。

(二) 第二阶段SFA回归结果

从上文对中部地带8个省市物流产业效率的分析过程中，可以发现中部地带物流产业技术效率整体水平不高，有一定的提升空间。为了剔除环境因素和随机扰动项对中部地带物流产业效率测算的影响，将决策单元处在相同的外部环境和运气成分，使得测算的中部地带物流产业效率更加精确、更能真实反映中部地带物流业情况。以第一阶段测算结果的各投入变量的松弛变量作为被解释变量，以经济发展水平和政府支持作为解释变量，建立SFA模型，运用Frontier 4.1软件对模型进行极大似然法(MLE)估计，测算的回归系数大于0时，表示外部环境(解释变量)增大将导致投入冗余增加；回归系数小于0时，表示外部环境(解释变量)增大将导致投入冗余减小。SFA模型回归的结果如表2所示。

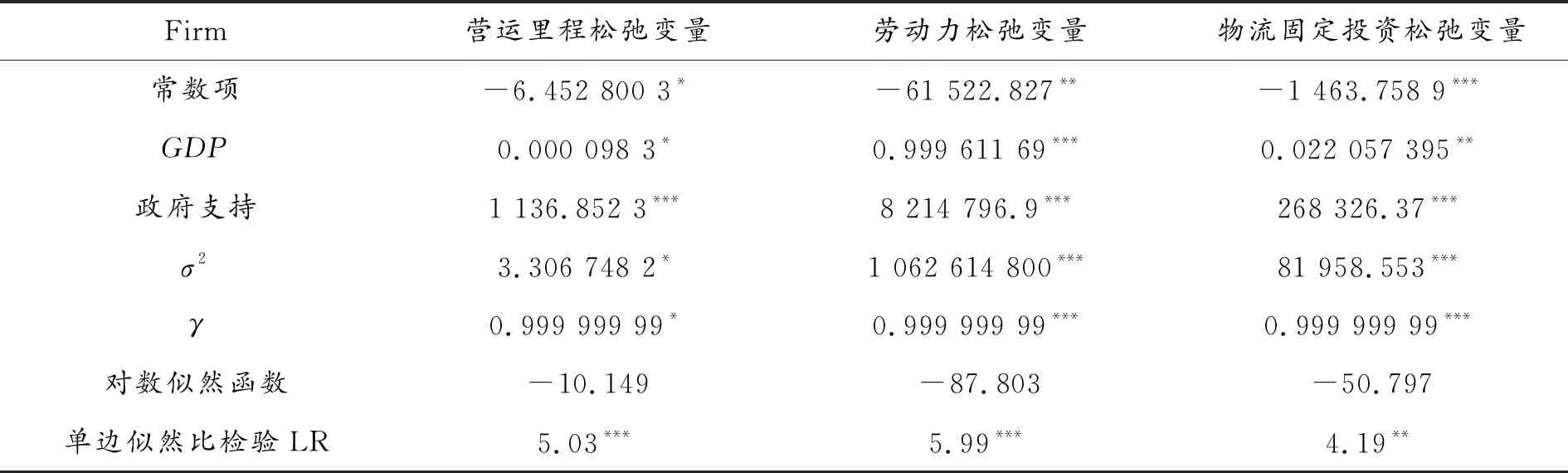
表2 SFA回归模型结果

从表2显示的结果可以看出，管理无效率对总方差的影响较大，管理因素是影响投入变量冗余的主要因素,回归方程结果的值均为0.999，接近于1，且通过1%的显著性水平的检验,说明了SFA模型使用的必要性。所有的环境变量和投入松弛变量回归系数均通过显著性检验，说明了环境变量的选取合理,各个环境指标对投入松弛变量冗余有显著的影响。从表2中可以看，经济发展水平和政府支持对3个投入指标——物流营运里程、物流业就业人员数、物流固定投资的松弛变量的回归系数为正数，表明经济发展水平提高和政府支持力度的增加使物流营运里程、物流业就业人员数、物流固定投资冗余增加，反映了我国“粗放型”的经济状况，存在盲目投资、重复建设等等问题。经济发展水平的提高和政府对物流业的支持引得大量的劳动力从事物流行业，致使物流行业劳动力冗余，不利于地区物流产业效率的提升。

本文从投入角度来测算物流产业效率。根据上文提到的管理无效率的分离公式和增加法剔除外部环境和随机因素公式，对原投入变量进行调整，得到新的决策单元的投入变量，各省的调整前后的投入变量如表3所示。

表3 调整前后投入变量

(三)第三阶段投入调整后的DEA实证结果

在经过第二阶段SFA模型对2013—2017年中部地带物流产业的投入变量进行调整后，调整后投入变量作为第三阶段测算中部地带的物流产业效率的投入变量，使用DEAP 2.1软件再次重复第一阶段过程，用投入角度BBC模型进行中部地带物流产业效率测算。第一阶段和第三阶段的结果如表4所示。

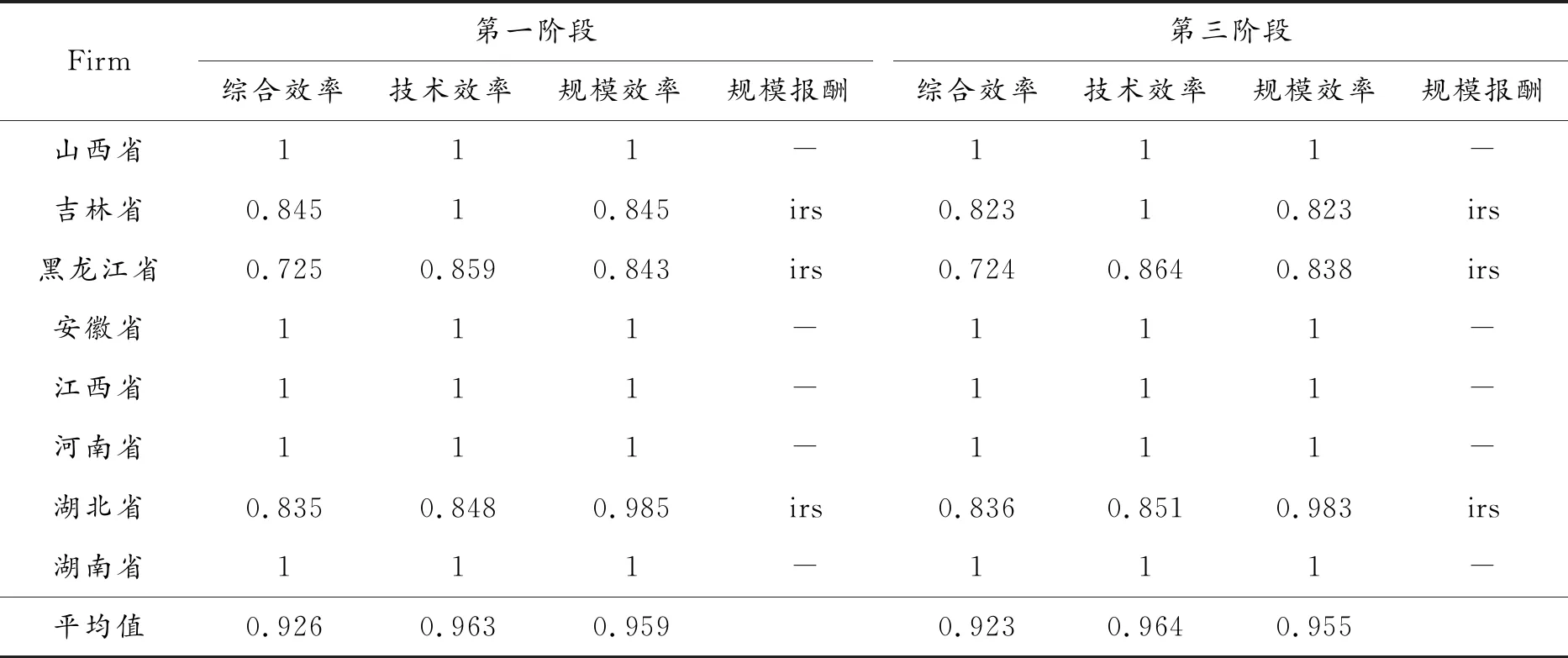
表4 第一阶段和第三阶段中部地带物流产业效率值

对表3中第一阶段和第三阶段中部地带各省市物流产业效率测算结果分析如下：

(1)从整个中部地带分析，第一阶段和第三阶段测算的中部地带物流产业效率平均值有明显的变化，综合效率平均值由原来的0.926下降到0.923，规模效率值由原有的0.959降至0.955，而技术效率值由原来的0.963增加为0.964，规模报酬整体保持不变。说明在未剔除外部环境和随机因素时，测算的中部地带物流产业效率的效率值不准确。中部地带物流产业效率各效率的平均值均在0.923以上，说明中部地带物流产业效率整体有着较高的水平。

(2)从各省份角度分析，各省份间物流产业效率差异较大。① 调整前后，山西省、安徽省、江西省、河南省和湖南省的物流产业效率仍然处在效率前沿面，说明这五省物流业在资源使用方面合理；② 吉林省、黑龙江省、湖北省三省物流产业效率未达到效率前沿面，而且效率相差较大，说明整个中部地带各省份间物流产业效率非常不协调。③ 调整后，黑龙江省和湖北省技术效率均高于第一阶段测算的效率，说明这两个省的实际技术效率优于表现出的水平，环境因素和随机因素对效率有负面影响。④ 吉林省、黑龙江省和湖北省的第三阶段测算的规模效率高于第一阶段测算的效率，说明这3个省的规模效率被高估，影响这3个省物流产业效率的关键因素是规模。⑤ 中部地带物流产业效率的规模报酬各省份不变，吉林省、黑龙江省和湖北省保持规模报酬递增状况，说明这3个省虽未达到效率的前沿面，但这3个省的物流业仍处于增长的状况。

五 、研究结论及建议

本文使用中部经济地带物流业2013—2017年的面板数据，采用三阶段DEA模型，对中部地带物流产业效率进行测算，剔除环境因素和随机因素的影响，使中部地带物流产业效率更加实际和准确，主要研究结论如下：

(1)根据第一、三阶段物流产业效率的对比发现，效率值存在不同层次变化。吉林省、黑龙江省和湖北省的规模效率均被高估，而且黑龙江省和湖北省技术效率均被低估，说明外部环境和随机因素对中部地带物流产业效率测算的影响较明显，使用三阶段DEA模型是有必要的。

(2)使用三阶段DEA模型对中部地带物流产业效率进行研究后发现，中部地带的物流产业效率有较高的水平，但地区间差异较大；虽然吉林省、黑龙江省和湖北省未达到效率前沿面，但是这些省份的状况均处于增长。除此之外，规模因素是制约整个中部地带物流产业效率提高的重要因素，中部地带应当合理增加物流业规模并做到技术进步，从而促进整个中部地带物流业又好又健康的发展。

六、研究局限及后期研究打算

本文的研究还存在一定的局限性。首先，对中部经济地带进行测算分析时，鉴于指标数据的可得性，未对碳排放、创新等方面未考虑在内；其次，在二阶段中，选择的影响因素不全面，在政府支持指标方面的选择上未能完全体现政策差异性；最后，在测算物流产业效率时，本文使用的三阶段DEA模型，未考虑其他评估方法。故拟在以后的研究中增加从可持续发展和创新的角度对物流产业效率进行研究，并在指标选择上，权衡各种因素使评价体系更加客观和科学，或者结合其他研究方法，使研究更能体现区域实际情况，同时完善本研究之不足，对物流产业效率进行更深入的研究。