基于运动补偿的动目标检测处理方法
2020-12-24董鹏曙谢幼才金加根
董鹏曙,向 龙,谢幼才,金加根
(空军预警学院,湖北 武汉 430019)
0 引言
动目标检测(MTD)是现代雷达信号处理中的重要方法,它能在完成多普勒滤波处理的同时,实现相参积累,有效提高了目标回波的信杂比,增强了雷达在杂波背景中探测运动目标的能力[1-2]。MTD完成多普勒滤波,实现相参积累的前提条件是在相参处理期间目标没有出现距离走动、多普勒走动现象。对常规情报雷达而言,其距离分辨率较低,距离分辨单元为百米量级,一般不会出现距离走动现象;但是,即使对常规飞行目标(约1Ma),由于目标与雷达的相对运动,也可能使得相参处理期间目标回波多普勒频率发生显著变化,分布到多个多普勒通道之中,MTD处理无法有效完成相参积累和目标检测。
针对高分辨雷达、成像雷达中目标高速运动引起的多普勒扩展问题,国内外学者开展了广泛的研究,目前主要有两类解决方法:一类是相关补偿法,先利用回波数据估计出目标的运动速度,再补偿回波中的高速运动成分,如单帧回波分段处理[4]、直接相关处理[5]等,其主要缺点是对信噪比要求较高,低信噪比时无法应用;另一类是变换搜索法,通过变换及搜索的方式补偿高速运动成分,如修正离散Chirp-Fourier变换[6]、距离-慢时间域Radon变换[7]、Radon-Fourier变换[9]、keystone变换[10]等,其主要问题是搜索策略的选取,搜索步距太小时运算量极大,对处理设备要求很高,搜索步距离太大时,可能漏掉最佳补偿点,无法完成补偿任务。关于常规情报雷达中飞行目标与雷达相对运动引起的多普勒频率变化,及其对相参积累的影响问题,未引起人们的重视。由于其MTD处理未考虑多普勒频率变化补偿问题,尽管对近距离强杂波有良好的抑制能力,但是对远距离弱目标的积累性能明显降低,甚至劣于非相参积累。为此,本文提出一种基于运动补偿的动目标检测处理方法,其基本思想是通过粗、精两级补偿消除目标回波在相参处理期间多普勒频率变化,再进行全距离MTD处理,以充分发挥MTD的相参积累性能,在保持对近距离强杂波良好抑制能力的同时,提高对远距离弱目标特别是隐身目标的探测能力。
1 目标运动对多普勒频率变化的影响分析
对运动目标回波而言,其多普勒频率为:
(1)
式(1)中,v为目标运动速度,θ为目标运动方向与雷达视线之间的夹角,λ为发射信号波长。在雷达发射信号波长一定的条件下,目标运动速度v和夹角θ的变化均可引起多普勒频率fd的变化。由式(1)全微分可得[5]:
(2)
式(2)中:Δfd(v)=2v′/λ,为目标加速度引起的回波多普勒频率变化率;Δfd(θ)=2vθ′/λ,为目标角速度引起的回波多普勒频率变化率;φ=arctan-1[Δfd(v)/Δfd(θ)],为Δfd(v)与Δfd(θ)决定的相角;v′为目标运动加速度;θ′为角速度(包括天线扫描角速度、目标机动角速度)。由于雷达波束对目标的一次扫略时间通常只有数十毫秒,在目标运动加速度、天线旋转角速度一定的条件下,相参积累期间目标回波多普勒频率近似呈线性变化。
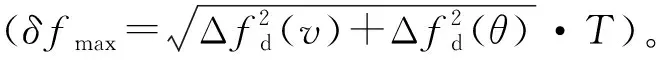
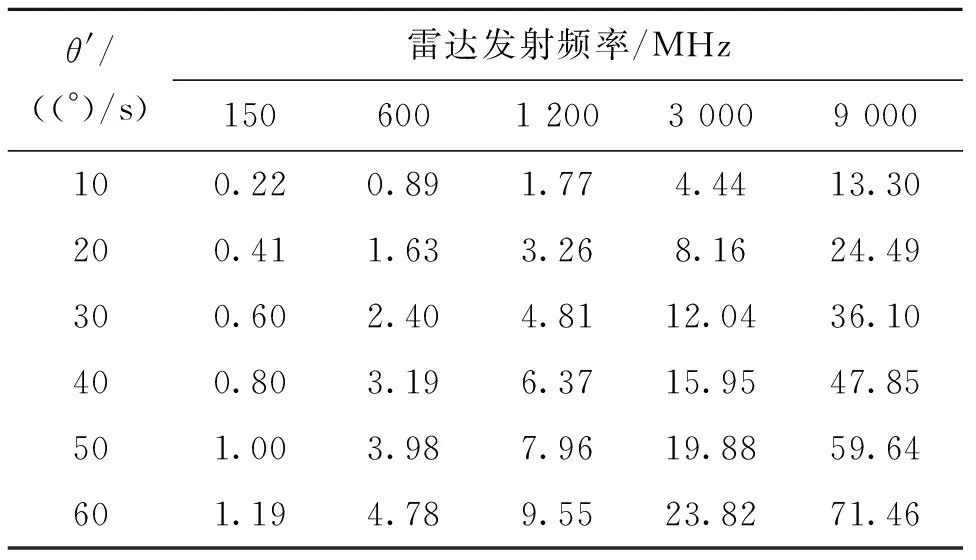
表1 加速度和角速度对脉间多普勒频率变化的综合影响Tab.1 Comprehensive effect of acceleration and angular velocity on pulse Doppler frequency variation
由表1可见:仅VHF波段、角速度在50(°)/s以下,以及P波段、角速度在10(°)/s以下时,相参处理间隔期内多普勒频率变化(Δf=16δfmax(θ))未超出一个多普勒分辨单元;P波段、角速度在20(°)/s以上及L、S、C、X波段,角速度在10(°)/s以上时,多普勒频率变化Δf均超出一个多普勒分辨单元,出现跨多普勒通道现象。
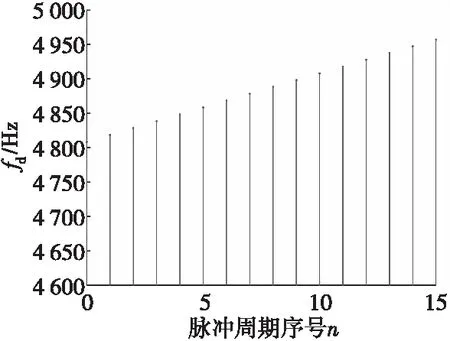
当加速度0~10g、角速度0~60(°)/s,雷达发射频率为3 000 MHz时,相邻两个重复周期之间目标回波多普勒频率变化情况如图1所示。角速度引起的目标回波多普勒频率变化远大于加速度引起的多普勒频率变化,因此角速度是影响目标回波多普勒频率变化的主要因素。
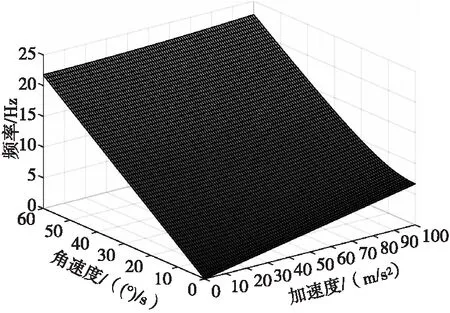
图1 目标运动加速度和角速度对多普勒频率的综合影响Fig.1 Target motion acceleration and angular velocity combined influence of Doppler frequency
综合考虑目标运动加速度、角速度对多普勒频率变化的影响,进行16点MTD处理,VHF、L、S、C、X各波段均会出现明显的多普勒走动现象;而且雷达工作频率越高,加速度、角速度越大,相参积累时间越长,多普勒走动现象越严重。为了获取相参积累得益,应进行多普勒补偿处理。
通过上述分析还可确定脉间多普勒频率变化的范围:
δf⊂[-δfmax,+δfmax]
(3)
2 基于运动补偿的MTD处理方法
基于运动补偿MTD处理的基本思想是通过多普勒补偿,以消除目标回波在相参处理期间多普勒频率变化,或使多普勒频率变化在一个多普勒分辨单元之内,具体分析如下。
2.1 多普勒补偿原理
将相参处理间隔期内N点回波信号记为S:
S=[s(0),s(1),s(2),…,s(n),…,s(N-1)]
(0≤n≤N-1)
(4)
考察复信号s(n),有:
s(n)=Aexp[j(2πfdnnT+φ)]
(5)
将相参处理期间N点回波的多普勒频率向量记为Fd:
Fd=[fd0,fd1,fd2,…,fdn,…,fdN-1]
(0≤n≤N-1)
(6)
以首点回波的多普勒频率fd0为基准,将N点回波的多普勒频率变化向量记为ΔFd,则有:
ΔFd=[0,Δfd1,Δfd2,…,Δfdn,…,ΔfdN-1]
(0≤n≤N-1)
(7)
式(7)中,Δfdn=fdn-fd0。
构造补偿向量K:
K=[1,exp(-j2πΔfd1T),…,exp(-j2πΔfdnT),
…,exp(-j2πΔfdN-1T)],(0≤n≤N-1)
(8)
进行如下运算:
Y=S·KT
(9)
即可补偿掉目标回波在相参处理期间的多普勒频率变化,将N点回波聚焦于一个多普勒通道之内。对杂波而言,补偿处理不能改变其功率谱特征。对白噪声而言,任何处理都不能消除其随机性,补偿处理后仍为白噪声。式中KT为K的转置。
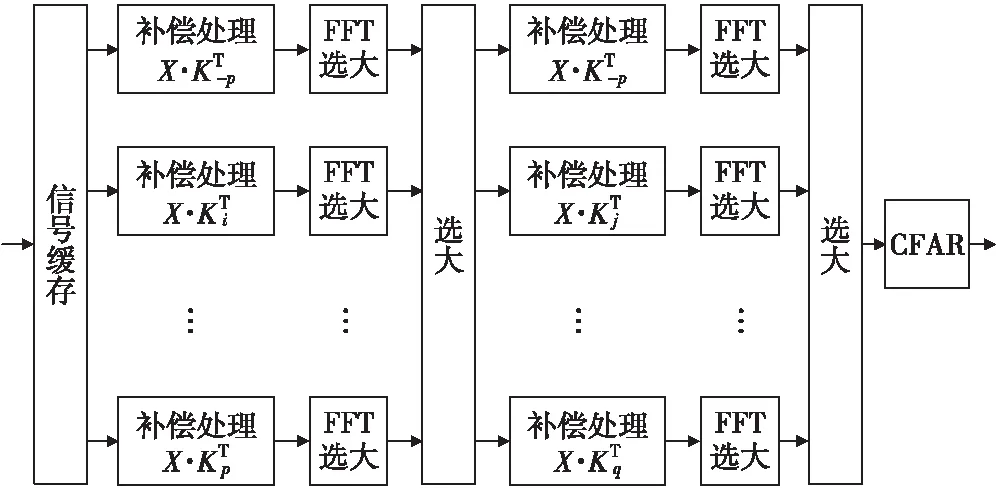
脉间多普勒频率变化可通过搜索的方式获得。假设相参处理期间,目标回波多普勒频率呈线性变化,搜索步距为i·σf,i为整数,σf为最小搜索间隔。则第i个搜索补偿向量为:
Ki=[1,exp(-j2πiσfT),…,
exp(-j2πiσf(N-1)T)]
(10)
进行如下搜索处理:
(11)
得到补偿后的积累峰值,经选大可得到最匹配的脉间多普勒频率变化δf=i·σf。
2.2 多普勒补偿精度要求分析
假设积累期间,目标回波的多普勒频率呈线性变化,相邻脉冲之间多普勒频率变化为δf,考察δf对相参积累的影响。
1) 当0<δf≤Fr/N2时,N点回波的多普勒频率变化向量为:
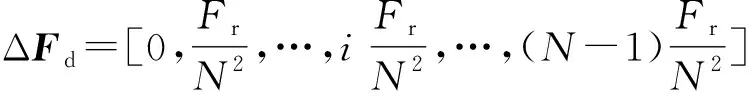
(12)
(13)
则N点回波经相参积累后功率谱处于一个通道之内,呈聚焦状态,无需补偿。
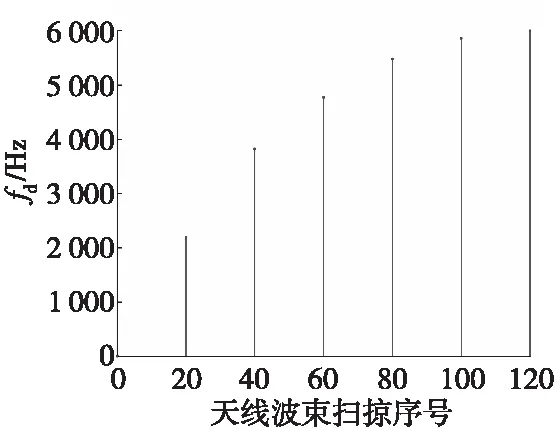
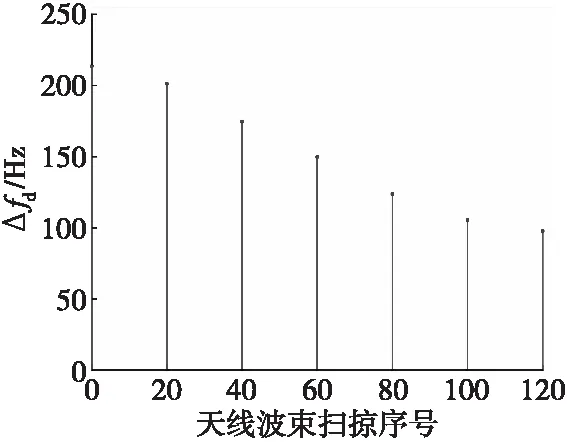
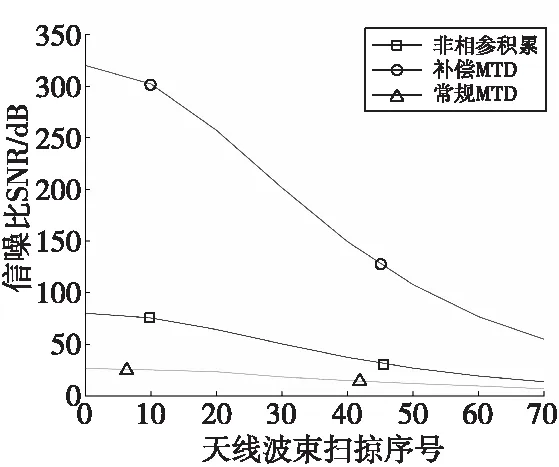
2) 当Fr/N2<δf (14) (15) 则N点回波经相参积累后功率谱分布在k个通道上,呈散焦状态,需要补偿。 3) 当δf=Fr/N时,N点回波的多普勒频率变化向量为: (16) 则N点回波经相参积累后功率谱均匀分布在N个通道,呈散焦状态,需要补偿。 4) 当δf为多普勒分辨单元的奇数倍,即δf=(2L-1)Fr/N时(N为偶数,L=1~N/2),由于折叠效应,N点回波的功率谱将均匀且等幅地分布于N个多普勒通道中,每个多普勒通道仅占信号总能量的1/N,呈散焦状态,需要补偿。 5) 当(2L-1)Fr/N<δf<2LFr/N时,令δf=(2L-1)Fr/N+kFr/N2,(N为偶数、L=1~N/2),可分解为2)、4)两种情形的叠加,则N点回波经相参积累后功率谱均匀分布在N个通道,再叠加k个通道的分布,呈散焦状态,需要补偿。 6) 当δf为多普勒分辨单元的偶数倍时,即δf=2LFr/N(N为偶数,L=1~N/2),N点回波经相参积累后功率谱覆盖的通道数随2L不同而各异,呈散焦状态,需要补偿。具体分布情况可参考文献[5]。 7) 当2LFr/N<δf<(2L+1)Fr/N时,令δf=2LFr/N+kFr/N2,(N为偶数、L=1~N/2),可分解为2)、6)两种情形叠加,呈散焦状态,需要补偿。 由上述分析可知,多普勒补偿的精度需优于Fr/N2。可按粗、精两级搜索的方式进行补偿,具体步骤如下: 1) 按雷达参数和典型目标运动参数求相邻脉冲之间的最大多普勒频率变化δfmax: (17) 2) 将δfmax以Fr/N、Fr/N2为基数进行归一化分解: (18) 3) 粗搜索P,其搜索范围为[-p,+p]; 4) 精搜索Q,其搜索范围为[-q,+q]。 基于粗精两级多普勒补偿的MTD处理流程如图2所示。经两级补偿、FFT处理、求模选大后,得到补偿积累峰值,然后经CFAR处理及检测确定是否存在目标,从而消除相邻脉冲之间多普勒频率变化的影响,使相参处理期间多普勒频率变化在一个多普勒分辨单元内,完成相参积累和信号检测。 图2 粗精两级多普勒补偿的MTD处理流程图Fig.2 Approximate and subtle compensation two-stage Doppler compensation MTD processing flow chart 由式(18)还可发现,当δfmax 实验一:雷达波束一次扫掠期间目标回波多普勒频率分布 以S波段两坐标雷达为例进行分析,假设其发射频率为3 000 MHz,波束宽度为2°,天线转速为6 r/min,重频为300 Hz。假定目标起始坐标为(0°,200 km),由西向东方向飞行,飞行速度约1Ma(340 m/s),目标运动轨迹如图3所示。雷达波束一次扫掠期间脉冲数约为16个。方位角为45°时,16个目标回波多普勒频率分布如图4所示。 图3 目标运动轨迹图Fig.3 Target trajectory 图4 目标回波多普勒频率分布图Fig.4 Doppler frequency distribution of target echo 雷达波束一次扫掠期间,16个回波的多普勒频率呈线性变化,其变化范围约为148 Hz,远大于16点MTD处理时的多普勒分辨单元(18.75 Hz),分布在8个多普勒分辨单元中,出现跨多普勒现象。 实验二:雷达波束多次扫掠期间目标回波多普勒频率及变化 实验条件同实验一。雷达波束多次扫掠期间,目标回波多普勒频率及其变化如图5、图6所示。方位角为0°时,雷达波束扫掠期间目标回波多普勒频率为0 Hz,多普勒频率变化约为213.6 Hz,分布在12个多普勒分辨单元中;方位角为30°时,目标回波多普勒频率为3 400 Hz,多普勒频率变化约为183 Hz,分布在10个多普勒分辨单元中;方位角为60°时,目标回波多普勒频率为5 889 Hz,多普勒频率变化约为104 Hz,分布在6个多普勒分辨单元中。 图5 目标回波多普勒频率分布图Fig.5 Doppler frequency distribution of target echo 图6 目标回波多普勒频率变化分布图Fig.6 Doppler frequency variation distribution of target echo 由此可见:目标切向飞行时,雷达波束扫掠期间目标回波多普勒频率最小,但多普勒频率变化最大,跨多普勒现象最严重;随着方位角的增大,雷达波束扫掠期间目标回波多普勒频率逐步增大,但多普勒频率变化逐步减小,跨多普勒程度逐渐减轻。 实验三:雷达波束多次扫掠时目标回波信噪比变化 假设该目标的起始信噪比为20 dB,在飞行过程中目标RCS不变,其他条件同上。非相参处理、常规MTD处理、补偿MTD处理均进行16点积累检测,雷达天线波束多次扫掠期间目标回波信噪比变化如图7所示,三种处理方式的检测点迹如图8所示。 图7 目标回波信噪比变化图Fig.7 Signal-to-noise ratio variation of target echo 图8 三种处理方式检测点迹图Fig.8 Detecting point trace of three processing methods 对16点积累检测进行仿真分析,以积累后信噪比13.2(即11.2 dB)为检测条件,采用非相参积累时目标消失点坐标约为(50.36°,313.5 km),采用常规MTD相参积累时目标消失点坐标约为(38.62°,256.0 km),采用多普勒补偿MTD相参积累时目标消失点坐标约为(63.11°,442.2 km)。 通过仿真分析可以看到: 1) 常规MTD处理的探测距离比非相参积累少67.5 km,其积累效果比非相参积累还差。由此说明了很多雷达在近距离采用MTD处理,远距离采用正常处理的原因。 2) 多普勒补偿MTD处理的探测距离比常规MTD处理多186.2 km,比非相参积累处理多128.7 km,其积累效果远优于非相参积累、常规MTD积累。进一步证明了采用多普勒补偿MTD处理的必要性和优越性。 3) 与Radon-Fourier变换补偿法相比[9],本文算法运算量仅为其运算量的数十分之一。 本文提出了基于运动补偿的MTD处理方法,该方法通过粗、精两级补偿后,可使相参处理期间的N点回波的多普勒频率均处于一个多普勒通道之内,有效消除了多普勒频率变化的影响,在保持对近距离强杂波良好抑制能力的同时,提高对远距离弱目标检测能力。仿真实验结果表明:该方法补偿策略清晰、计算量小、易于工程实现,而且也适用于低信噪比条件;其不足之处是只适用于目标回波脉间多普勒频率近于线性变化的情况,对于具有更高阶的高机动目标补偿方法,还需进一步研究。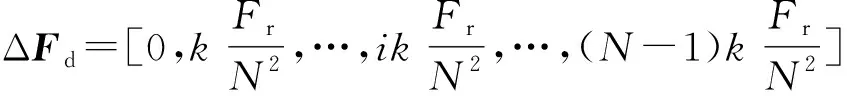

2.3 基于运动补偿的MTD处理方法
3 仿真实验与分析

4 结论
